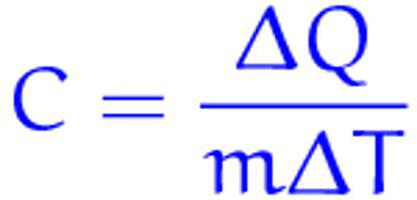на что влияет удельная теплоемкость
Удельная теплоемкость вещества
Нагревание и охлаждение
Эти два процесса знакомы каждому. Вот нам захотелось чайку, и мы ставим чайник, чтобы нагреть воду. Или ставим газировку в холодильник, чтобы охладить.
Логично предположить, что нагревание — это увеличение температуры, а охлаждение — ее уменьшение. Все, процесс понятен, едем дальше.
Но не тут-то было: температура меняется не «с потолка». Все завязано на таком понятии, как количество теплоты. При нагревании тело получает количество теплоты, а при нагревании — отдает.
В процессах нагревания и охлаждения формулы для количества теплоты выглядят так:
Нагревание
Охлаждение
Q — количество теплоты [Дж]
c — удельная теплоемкость вещества [Дж/кг*˚C]
tконечная — конечная температура [˚C]
tначальная — начальная температура [˚C]
В этих формулах фигурирует и изменение температуры, о котором мы сказали выше, и удельная теплоемкость, речь о которой пойдет дальше.
А вот теперь поговорим о видах теплопередачи.
Виды теплопередачи
Здесь все совсем несложно, их всего три: теплопроводность, конвекция и излучение.
Теплопроводность
Тот вид теплопередачи, который можно охарактеризовать, как способность тел проводить энергию от более нагретого тела к менее нагретому.
Речь о том, чтобы передать тепло с помощью соприкосновения. Признавайтесь, грелись же когда-нибудь возле батареи. Если вы сидели к ней вплотную, то согрелись вы благодаря теплопроводности. Обниматься с котиком, у которого горячее пузо, тоже эффективно.
Порой мы немного перебарщиваем с возможностями этого эффекта, когда на пляже ложимся на горячий песок. Эффект есть, только не очень приятный. Ну а ледяная грелка на лбу дает обратный эффект — ваш лоб отдает тепло грелке.
Конвекция
Когда мы говорили о теплопроводности, мы приводили в пример батарею. Теплопроводность — это когда мы получаем тепло, прикоснувшись к батарее. Но все вещи в комнате к батарее не прикасаются, а комната греется. Здесь вступает конвекция.
Дело в том, что холодный воздух тяжелее горячего (холодный просто плотнее). Когда батарея нагревает некий объем воздуха, он тут же поднимается наверх, проходит вдоль потолка, успевает остыть и спуститься обратно вниз — к батарее, где снова нагревается. Таким образом, вся комната равномерно прогревается, потому что все более горячие потоки сменяют все менее холодные.
Излучение
Пляж мы уже упоминали, но речь шла только о горячем песочке. А вот тепло от солнышка — это излучение. В этом случае тепло передается через волны.
Обоими способами. То тепло, которое мы ощущаем непосредственно от камина (когда лицу горячо, если вы расположились слишком близко к камину) — это излучение. А вот прогревание комнаты в целом — это конвекция.
Удельная теплоемкость: понятие и формула для расчета
Формулы количества теплоты для нагревания и охлаждения мы уже разбирали, но давайте еще раз:
Нагревание
Охлаждение
Q — количество теплоты [Дж]
c — удельная теплоемкость вещества [Дж/кг*˚C]
tконечная — конечная температура [˚C]
tначальная — начальная температура [˚C]
В этих формулах фигурирует такая величина, как удельная теплоемкость. По сути своей — это способность материала получать или отдавать тепло.
С точки зрения математики удельная теплоемкость вещества — это количество теплоты, которое надо к нему подвести, чтобы изменить температуру 1 кг вещества на 1 градус Цельсия:
Удельная теплоемкость вещества
Q — количество теплоты [Дж]
c — удельная теплоемкость вещества [Дж/кг*˚C]
tконечная — конечная температура [˚C]
tначальная — начальная температура [˚C]
Также ее можно рассчитать через теплоемкость вещества:
Удельная теплоемкость вещества
c — удельная теплоемкость вещества [Дж/кг*˚C]
C — теплоемкость вещества [Дж/˚C]
Величины теплоемкость и удельная теплоемкость означают практически одно и то же. Отличие в том, что теплоемкость — это способность всего вещества к передаче тепла. То есть формулу количества теплоты для нагревания тела можно записать в таком виде:
Количество теплоты, необходимое для нагревания тела
Q — количество теплоты [Дж]
c — удельная теплоемкость вещества [Дж/кг*˚C]
tконечная — конечная температура [˚C]
tначальная — начальная температура [˚C]
Таблица удельных теплоемкостей
Удельная теплоемкость — табличная величина. Часто ее указывают в условии задачи, но при отсутствии в условии — можно и нужно воспользоваться таблицей. Ниже приведена таблица удельных теплоемкостей для некоторых (многих) веществ.
Удельная теплоемкость: для чего она нужна и в чем ее смысл?
Однако толкованию слова «удельный» обычно уделяется недостаточно внимания. Учащиеся просто запоминают его как данность. А что оно значит?
Если заглянуть в словарь Ожегова, то можно прочесть, что такая величина определяется как отношение. Причем оно может быть выполнено к массе, объему или энергии. Все эти величины обязательно полагается брать равными единице. Отношение к чему задается в удельной теплоемкости?
К произведению массы и температуры. Причем их значения обязательно должны быть равными единице. То есть в делителе будет стоять число 1, но его размерность будет сочетать килограмм и градус Цельсия. Это обязательно учитывается при формулировке определения удельной теплоемкости, которое дано немного ниже. Там же находится формула, из которой видно, что в знаменателе стоят именно эти две величины.
Что это такое?
Удельная теплоемкость вещества вводится в тот момент, когда рассматривается ситуация с его нагреванием. Без него невозможно узнать, какое количество теплоты (или энергии) потребуется затратить на этот процесс. А также вычислить ее значение при охлаждении тела. Кстати, эти два количества теплоты равны друг другу по модулю. Но имеют разные знаки. Так, в первом случае она положительная, потому что энергию нужно затратить и она передается телу. Вторая ситуация с охлаждением дает отрицательное число, потому что тепло выделяется, и внутренняя энергия тела уменьшается.
Обозначается эта физическая величина латинской буквой c. Определяется она как некоторое количество теплоты, необходимое для нагревания одного килограмма вещества на один градус. В курсе школьной физики в качестве этого градуса выступает тот, что берется по шкале Цельсия.
Как ее сосчитать?
Если требуется узнать, чему равна удельная теплоемкость, формула выглядит так:
с = Q / (m * (t2 – t1)), где Q — количество теплоты, m — масса вещества, t2 – температура, которую тело приобрело в результате теплообмена, t1 — начальная температура вещества. Это формула № 1.
Исходя из этой формулы, единица измерения этой величины в международной системе единиц (СИ) оказывается Дж/(кг*ºС).
Как найти другие величины из этого равенства?
Во-первых, количество теплоты. Формула будет выглядеть таким образом: Q = с * m * (t2 – t1). Только в нее необходимо подставлять величины в единицах, входящих в СИ. То есть масса в килограммах, температура — в градусах Цельсия. Это формула № 2.
Во-вторых, массу вещества, которое остывает или нагревается. Формула для нее будет такой: m = Q / (c * (t2 – t1)). Это формула под № 3.
В-третьих, изменение температуры Δt = t2 – t1 = (Q / c * m). Знак «Δ» читается как «дельта» и обозначает изменение величины, в данном случае температуры. Формула № 4.
Какие значения она может иметь?
Экспериментальным путем установлено, какие она имеет значения у каждого конкретного вещества. Поэтому создана специальная таблица удельной теплоемкости. Чаще всего в ней даны данные, которые справедливы при нормальных условиях.
| Вещество | Удельная теплоемкость, Дж/(кг * ºС) |
| алюминий | 920 |
| вода | 4200 |
| графит | 750 |
| железо | 460 |
| золото | 130 |
| латунь | 400 |
| лед | 2100 |
| медь | 400 |
| олово | 230 |
| свинец | 140 |
| сталь | 500 |
| стекло лабораторное | 840 |
| чугун | 540 |
В чем заключается лабораторная работа по измерению удельной теплоемкости?
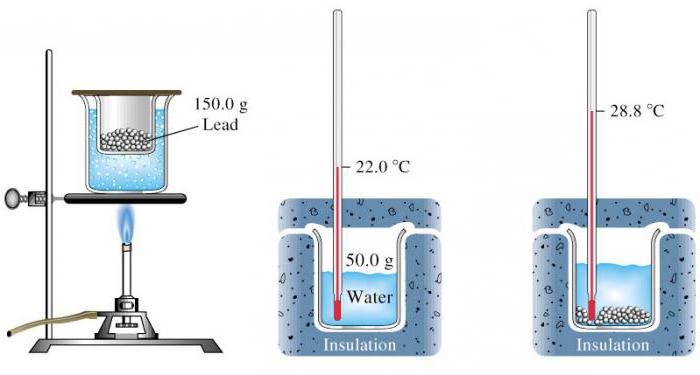
В школьном курсе физики ее определяют для твердого тела. Причем его теплоемкость высчитывается благодаря сравнению с той, которая известна. Проще всего это реализуется с водой.
В процессе выполнения работы требуется измерить начальные температуры воды и нагретого твердого тела. Потом опустить его в жидкость и дождаться теплового равновесия. Весь эксперимент проводится в калориметре, поэтому потерями энергии можно пренебречь.
Потом требуется записать формулу количества теплоты, которое получает вода при нагревании от твердого тела. Второе выражение описывает энергию, которую отдает тело при остывании. Эти два значения равны. Путем математических вычислений остается определить удельную теплоемкость вещества, из которого состоит твердое тело.
Чаще всего ее предлагается сравнить с табличными значениями, чтобы попытаться угадать, из какого вещества сделано изучаемое тело.
Задача № 1
Условие. Температура металла изменяется от 20 до 24 градусов Цельсия. При этом его внутренняя энергия увеличилась на 152 Дж. Чему равна удельная теплоемкость металла, если его масса равна 100 граммам?
Решение. Для нахождения ответа потребуется воспользоваться формулой, записанной под номером 1. Все величины, необходимые для расчетов, есть. Только сначала необходимо перевести массу в килограммы, иначе ответ получится неправильный. Потому что все величины должны быть такими, которые приняты в СИ.
В одном килограмме 1000 граммов. Значит, 100 граммов нужно разделить на 1000, получится 0,1 килограмма.
Подстановка всех величин дает такое выражение: с = 152 / (0,1 * (24 – 20)). Вычисления не представляют особой трудности. Результатом всех действий является число 380.
Ответ: с = 380 Дж/(кг * ºС).
Задача № 2
Условие. Определить конечную температуру, до которой остынет вода объемом 5 литров, если она была взята при 100 ºС и выделила в окружающую среду 1680 кДж тепла.
Решение. Начать стоит с того, что энергия дана в несистемной единице. Килоджоули нужно перевести в джоули: 1680 кДж = 1680000 Дж.
Подстановка значений в формулу массы дает такое выражение: 1000 * 0,005 = 5 кг. Удельную теплоемкость потребуется посмотреть в таблице. Теперь можно переходить к формуле 8: t2 = 100 + (1680000 / 4200 * 5).
Задача № 3
Условие. Имеется химический стакан массой 100 г. В него налито 50 г воды. Начальная температура воды со стаканом равна 0 градусам Цельсия. Какое количество теплоты потребуется для того, чтобы довести воду до кипения?
Решение. Начать стоит с того, чтобы ввести подходящее обозначение. Пусть данные, относящиеся к стакану, будут иметь индекс 1, а к воде — индекс 2. В таблице необходимо найти удельные теплоемкости. Химический стакан сделан из лабораторного стекла, поэтому его значение с1 = 840 Дж/ (кг * ºС). Данные для воды такие: с2 = 4200 Дж/ (кг * ºС).
Их массы даны в граммах. Требуется перевести их в килограммы. Массы этих веществ будут обозначены так: m1 = 0,1 кг, m2 = 0,05 кг.
Начальная температура дана: t1 = 0 ºС. О конечной известно, что она соответствует той, при которой вода кипит. Это t2 = 100 ºС.
Поскольку стакан нагревается вместе с водой, то искомое количество теплоты будет складываться из двух. Первой, которая требуется для нагревания стекла (Q1), и второй, идущей на нагревание воды (Q2). Для их выражения потребуется вторая формула. Ее необходимо записать два раза с разными индексами, а потом составить их сумму.
Получается, что Q = с1 * m1 * (t2 – t1) + с2 * m2 * (t2 – t1). Общий множитель (t2 – t1) можно вынести за скобку, чтобы было удобнее считать. Тогда формула, которая потребуется для расчета количества теплоты, примет такой вид: Q = (с1 * m1 + с2 * m2) * (t2 – t1). Теперь можно подставить известные в задаче величины и сосчитать результат.
Q = (840 * 0,1 + 4200 * 0,05) * (100 – 0) = (84 + 210) * 100 = 294 * 100 = 29400 (Дж).
Количество теплоты и удельная теплоемкость
Вместо словосочетания «тепловая энергия» физики говорят сокращенно: «теплота».
Удобно сравнивать между собой величины, которые измерены численно. Поэтому, физики говорят о количестве тепловой энергии, или количестве теплоты.
Что такое количество теплоты
Рассмотрим чашку, в которой находится обыкновенная вода комнатной температуры.
Вычислим внутреннюю энергию холодной воды в чашке, получим число, которое можно обозначить так:
\(\large U_<\text<хол>> \left( \text <Дж>\right) \) – внутренняя энергия холодной воды.
Нагреем воду в чашке. Молекулы нагретой воды будут двигаться быстрее. Значит, горячая вода обладает большим количеством внутренней энергии.
Теперь посчитаем внутреннюю энергию горячей воды в чашке. Полученное число обозначим, как
\(\large U_<\text<горяч>> \left( \text <Дж>\right) \) – внутренняя энергия горячей воды.
Найдем разницу внутренней энергии для горячей и холодной воды.
Примечание: Вместо слова «разница» математики скажут «разность».
Мы получим еще одно число. Обозначим его символом Q. Число Q называют количеством теплоты. Именно эту тепловую энергию вода получила во время нагревания.
Примечание: Когда горячая вода остынет, она отдаст ровно столько тепловой энергии, сколько получила во время нагревания. Потому, что выполняется закон сохранения тепловой энергии.
\(\large Q \left( \text <Дж>\right) \) – тепловая энергия, количество теплоты.
Теплота, как и любая энергия, измеряется в системе СИ в Джоулях, в честь английского физика Джеймса Джоуля.
Примечание: Количество теплоты, так же, измеряют в Калориях.
Калория – это тепловая энергия, затраченная на нагревание 1 грамма воды на 1 градус Цельсия.
Джоуль и Калория связаны так:
От чего зависит количество теплоты
Количество теплоты, требуемое для нагревания тела, зависит от нескольких параметров.
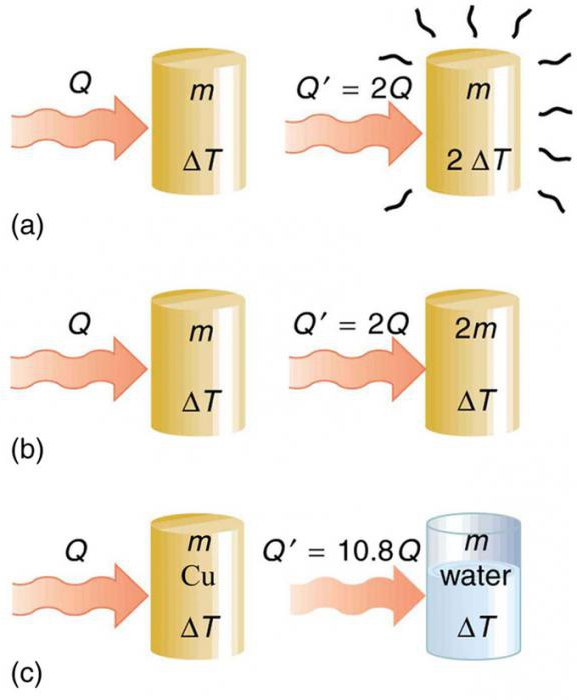
От массы вещества
Нальем в одну кастрюльку 1 кг воды, а в другую, точно такую же кастрюльку – 2 килограмма воды.
Пусть, начальная температура воды о обеих кастрюльках равна +20 градусам Цельсия.
Будем нагревать эти кастрюльки по очереди на газовой плите, не меняя интенсивность огня конфорки.
Предположим, нам нужно повысить на 50 градусов Цельсия температуру воды в каждой кастрюльке.
Примечание: После нагревания воды на 50 градусов, конечная температура воды в каждой кастрюльке будет равна 70 градусам.
Чтобы нагреть на 50 градусов 1 килограмм воды, потребуется время. Однако, чтобы нагреть на этой же конфорке 2 килограмма воды на 50 градусов, потребуется больше времени.
Значит, количество теплоты, полученное водой, зависит от массы вещества, которое мы хотим нагреть.
Математики запишут фразу «количество теплоты зависит от массы» так:
Символом f обозначается зависимость.
\(\large m \left( \text <кг>\right) \) – масса нагреваемого вещества.
От разницы температур
Теперь возьмем две кастрюльки, и нальем в них по 1 кг воды. Начальная температура воды в кастрюльках одинаковая и равна +20 градусов Цельсия.
Одну кастрюльку будем нагревать дольше другой. Поэтому, температура воды будет выше в той кастрюльке, которую дольше нагревали.
Так как температура повысилась больше в кастрюльке, которую дольше нагревали, то физики скажут, что воде в этой кастрюльке передали большее количество теплоты.
Значит, количество теплоты зависит от разницы (т. е. разности) между начальной и конечной температурой.
\(\large t_<\text<конеч>> \left( \text <град>\right) \) – температура после нагревания;
\(\large t_<\text<нач>> \left( \text <град>\right) \) – температура до нагревания;
\(\large \Delta t \left( \text <град>\right) \) – разность температуры;
Математики фразу «количество теплоты зависит от разности температур» запишут так:
Символ f обозначает, что Q зависит от разницы температур.
От вида вещества
Теперь будем нагревать 1 килограмм воды и 1 килограмм подсолнечного масла.
Первоначальная температура каждого вещества +20 градусов Цельсия.
Измерим через 5 минут нагревания температуру воды и температуру масла.
Оказывается, за 5 минут масло нагреется до более высокой температуры. При этом и масло, и вода, получили одинаковое количество теплоты.
Значит, количество теплоты зависит от того, из какого вещества состоит тело.
Какие величины называют удельными
Физики часто применяют удельные величины, так как они достаточно удобны для вычислений.
Удельная величина – величина, приходящаяся на единицу массы, длины, площади, или объема.
В обычной жизни мы, так же, пользуемся удельными величинами. К примеру, цена товара – это удельная величина, так как она приходится на единицу товара. Зная количество товара, легко посчитать общую цену покупки.
Например, булочка стоит 20 рублей. Нужно купить 3 булочки. Общую сумму денег найдем, перемножив цену одной булочки (удельную величину) на количество штук.
Известно, что при горении топлива выделяется энергия. Удельная теплота сгорания и количество сгоревших килограммов топлива помогут посчитать выделившуюся тепловую энергию.
Что такое удельная теплоемкость
Возьмем 1 килограмм вещества и нагреем его на 1 градус Цельсия. Тепловая энергия, которую мы для этого затратили, называется удельной теплоемкостью.
Удельная теплоемкость – это энергия, затраченная для нагревания 1 килограмма на 1 градус.
Эту энергию обозначают латинским символом «c». Измеряют ее в Джоулях, деленных на килограмм и градус.
\(\large c \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \) – удельная теплоемкость;
Примечания:
Удельные теплоемкости воды в различных агрегатных состояниях
В твердом состоянии (лед), вода будет иметь такую теплоемкость:
В жидком состоянии (вода), такую:
В газообразном состоянии (пар) при температуре 100 градусов Цельсия, такую:
Примечание: Удельные теплоемкости различных веществ можно найти в школьном справочнике физики.
Как связаны и чем отличаются количество теплоты и удельная теплоемкость
Будем рассматривать такие процессы, как нагревание и охлаждение.
Благодаря процессам нагревания и охлаждения мы можем обогреваться зимой с помощью русской печи. Сначала печь получит количество теплоты (тепловую энергию) от сгорающего топлива — дров. А затем, будет остывать и отдавать это количество теплоты всем телам, находящимся в помещении.
Отличия удельной теплоемкости от количества теплоты
Запомнить, что такое количество теплоты, и чем оно отличается от удельной теплоемкости, можно так (рис. ):
Связь количества теплоты и удельной теплоемкости — формула
то легко посчитать общую тепловую энергию – т. е. количество теплоты.
Для этого используем формулу:
\(\large Q \left( \text <Дж>\right) \) – количество теплоты, т. е. общая тепловая энергия;
\(\large c \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \) – удельная теплоемкость;
\(\large m \left( \text <кг>\right) \) – масса вещества;
\(\large t_<\text<конеч>> \left( \text <град>\right) \) – температура после нагревания;
\(\large t_<\text<нач>> \left( \text <град>\right) \) – температура до нагревания;
Как по графику нагревания или охлаждения определить удельную теплоемкость
На примере покажем, как находить удельную теплоемкость по графику нагревания или охлаждения тела.
Дано твердое тело массой 2 килограмма. На рисунке 5 указано, как зависит температура этого тела от полученного количества теплоты. По горизонтали отложено количество теплоты, а по вертикали – температура некоторого тела, находящегося в твердом состоянии.
Определить удельную теплоемкость вещества, из которого состоит данное твердое тело.
Решение:
Тело нагрелось от \(\large t_ <1>= 0 \left( С \right) \) до температуры \(\large t_ <2>= 60 \left( С \right) \);
Разность температур равна 60 градусам Цельсия.
Масса тела 2 килограмма.
Полученное количество теплоты \(\large Q = 15000 \left( \text <Дж>\right) \).
Выпишем формулу, по которой можно посчитать тепловую энергию Q:
Подставим теперь значения в эту формулу для определения количества теплоты:
\[\large 15000 = c \cdot 2 \cdot 60 \]
Разделим обе части уравнения на число 10:
\[\large 1500 = c \cdot 2 \cdot 6 \]
Теперь разделим обе части уравнения на число 6:
\[\large 250 = c \cdot 2 \]
Разделив обе части на число 2, получим удельную теплоемкость твердого вещества:
Ответ: Удельная теплоемкость твердого вещества \(\large 125 \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \)
Примечание: Тела могут обмениваться тепловой энергией с другими телами. Обмен энергией прекратится при наступлении теплового равновесия. Для решения задач нужно использовать удельные теплоемкости материалов, из которых изготовлены тела. А чтобы рассчитать переданное или полученное телом количество теплоты, нужно уметь применять закон сохранения энергии и составлять уравнение теплового баланса.
Удельная теплоемкость
СОДЕРЖАНИЕ
Определение [ править ]
Варианты [ править ]
Применимость [ править ]
Удельную теплоемкость можно определить и измерить для газов, жидкостей и твердых тел довольно общего состава и молекулярной структуры. К ним относятся газовые смеси, растворы и сплавы или гетерогенные материалы, такие как молоко, песок, гранит и бетон, если рассматривать их в достаточно большом масштабе.
Удельная теплоемкость также может быть определена для материалов, которые изменяют состояние или состав при изменении температуры и давления, если эти изменения обратимы и постепенны. Таким образом, например, концепции могут быть определены для газа или жидкости, которые диссоциируют при повышении температуры, до тех пор, пока продукты диссоциации быстро и полностью рекомбинируют, когда температура падает.
Измерение [ править ]
Удельную теплоемкость газов можно измерить при постоянном объеме, поместив образец в жесткий контейнер. С другой стороны, измерение удельной теплоемкости при постоянном объеме может быть чрезмерно трудным для жидкостей и твердых тел, поскольку часто требуется непрактичное давление, чтобы предотвратить расширение, которое может быть вызвано даже небольшим повышением температуры. Вместо этого обычно измеряют удельную теплоемкость при постоянном давлении (позволяя материалу расширяться или сжиматься по своему желанию), отдельно определять коэффициент теплового расширения и сжимаемость материала и вычислять удельную теплоемкость при постоянном объеме из эти данные согласно законам термодинамики. [ необходима цитата ]
Единицы [ править ]
Международная система [ править ]
Имперские инженерные единицы [ править ]
В этих контекстах единицей удельной теплоемкости является БТЕ / ° F / фунт = 4177,6 Дж / К / кг. Первоначально БТЕ была определена таким образом, чтобы средняя удельная теплоемкость воды составляла 1 БТЕ / ° F / фунт.
Калории [ править ]
Хотя эти единицы все еще используются в некоторых контекстах (например, килограмм калорий в питании ), их использование в настоящее время не рекомендуется в технических и научных областях. Когда тепло измеряется в этих единицах, единицей удельной теплоемкости обычно является
1 кал / ° C / г («малая калория») = 1 кал / ° C / кг = 1 ккал / ° C / кг («большая калория») = 4184 Дж / K / кг.
В обоих единицах удельная теплоемкость воды составляет приблизительно 1. Комбинации кал / ° C / кг = 4,184 Дж / K / кг и ккал / ° C / г = 4184000 Дж / K / кг не кажутся широко распространенными. использовал.
Физическая основа удельной теплоемкости [ править ]
Одноатомные газы [ править ]
Для благородных газов, от гелия до ксенона, эти расчетные значения равны
Многоатомные газы [ править ]
С другой стороны, многоатомная молекула газа (состоящая из двух или более атомов, связанных вместе) может накапливать тепловую энергию в других формах, помимо своей кинетической энергии. Эти формы включают вращение молекулы и колебание атомов относительно ее центра масс.
Эти дополнительные степени свободы или «моды» вносят вклад в удельную теплоемкость вещества. А именно, когда в газ с многоатомными молекулами вводится тепловая энергия, только часть ее идет на увеличение их кинетической энергии и, следовательно, температуры; остальное перейдет в те другие степени свободы. Для достижения такого же повышения температуры моль этого вещества должен быть обеспечен большей тепловой энергией, чем моль одноатомного газа. Следовательно, теплоемкость многоатомного газа зависит не только от его молекулярной массы, но и от числа степеней свободы, которыми обладают молекулы. [15] [16] [17]
Квантовая механика далее утверждает, что каждая вращательная или колебательная мода может принимать или терять энергию только в определенном дискретном количестве (квантах). В зависимости от температуры средняя тепловая энергия на молекулу может быть слишком маленькой по сравнению с квантами, необходимыми для активации некоторых из этих степеней свободы. Эти режимы называются «замороженными». В этом случае удельная теплоемкость вещества будет увеличиваться с температурой, иногда ступенчато, по мере того, как большее количество режимов размораживается и начинает поглощать часть подводимой тепловой энергии.
Термодинамическое происхождение [ править ]
Состояние вещества в однородном образце [ править ]
Сохранение энергии [ править ]
Если давление остается постоянным, второй член в левой части равен нулю, и
Связь с уравнением состояния [ править ]
Связь между теплоемкостями [ править ]
Это уравнение можно переписать как
Расчет из первых принципов [ править ]
Идеальный газ [ править ]
это уравнение сводится просто к соотношению Майера :