теоремы логическая структура теоремы методика обучения доказательству теорем

Лекция №5. Математические предложения и методика изучения теорем

1.Виды математических предложений

2.Логическая структура теорем. Виды теорем и связь между ними

3.Необходимые и достаточные условия, теоремы – свойства и теоремы – признаки

4.Методика обучения доказательству

I.Каждая математическая теория представляет собой множество предложений, описывающих структуру этой теории. С каждым математическим предложением связаны содержание (выраженное в нем математическое содержание) и логическая форма (или структура). В математике различают элементарные и составные предложения. Составные предложения образуются из элементарных с помощью логических связок “не”, “и”, “или”, “если …, то”, “тогда и только тогда”, “для всякого”, обозначающих логические операции.

Выявить логическую структуру составного предложения – значит установить:

1) Из каких элементарных предложений образовано данное составное предложение;

2) С помощью каких логических связано.

а)“ 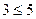” б) “ ”

Это сложное предложение:

а) 1) 2) а) 1) 2)

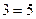
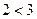
б) или (дизъюнкция) б) и (конъюнкция)

К математическим предложениям относятся:

· Теорема – математическое предложение, истинность которого доказывается,

· Аксиома– математическое предложение, истинность которого принимается без доказательства,

· Определения математических понятий.

Среди суждений, устанавливающих различные отношения между математическими понятиями, выделяют высказывания и высказывательные формы.

Определение. Высказываниемназывается предложение, относительно которого имеет смысл вопрос, истинно оно или ложно.

— ложное высказывание.

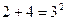
Определение. Высказывательная форма – это предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке в него конкретных значений переменных.

— одноместная высказывательная форма

— двуместная высказывательная форма

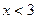
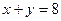
II.Каждая теорема состоит из 3 частей:

В разъяснительной части описывается, какие точки или фигуры рассматриваются в теореме. Для словесного выражения теорем обычно используют две формы суждений: категоричную, условную (импликативную).

Категоричная – когда принадлежность или непринадлежность некоторого признака предмету независимо от каких бы то ни было условий.

Условная – когда истинность суждения ставится в зависимости от определенных условий.

Если теорема содержит несколько условий и заключений, то теорема сложная.

Логико – математический анализ теоремы предполагает:

1) установление формы суждения;

2) выделение разъяснительной части, условия, заключений;

3) установление факта, какая дана теорема – простая или сложная.

— прямая теорема

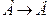
Если разъяснительную часть оставить без изменения, а условие и заключение поменять местами, то получим утверждение обратное данному. ( )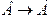

Если разъяснительную часть оставить без изменения, а условие и заключение утверждения заменить их отрицанием, то получим утверждение противоположное данному.

Если оставить без изменения разъяснительную часть и поменять местами условие и заключение утверждения, противоположного данному, то получим утверждение, обратное противоположному.

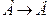
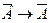
Утверждения , всегда одновременно истинны или ложны. Эта связь между теоремами используется при доказательстве методом от противного. Если первую теорему трудно доказать, то её заменяем на обратную противоположной.

Схема метода доказательства от противного:

1) предлагаем противоположное тому, что требуется доказать, т.е. …

2) из предложения следует, что …

3) получаем противоречие с …

4) значит наше предположение неверно, а верно то, что требовалось доказать, т.е …

III.Если из предложения следует предложение , то говорят, что — достаточное условие для , а — необходимое условие для .

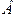
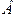
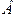
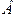
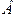
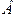
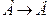
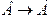
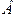
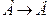
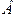
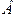
Другими словами, предложение называется необходимым условием для , если оно логически следует из . Предложение называется достаточным условием для ,если из него следует.

Если “и”, “и”, то говорят, что является необходимым и достаточным условием для , и наоборот.

Пример: Если число делится на 10, то оно делится на 2.

истинно, т.е. — достаточное для ,

— необходимое для .

Определение. Под свойствомпонимается обязательное условие принадлежности объекта к данному виду.

Другими словами, свойство – это то, что мы можем получить (или доказать), исходя из того, что объект принадлежит к данному виду.

Например, мы знаем, что 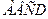— ромб. Следовательно, мы можем утверждать, что:

¾ — четырехугольник

¾ — параллелограмм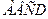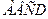

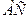
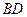
¾ диагонали и перпендикулярны

Все это – свойства ромба. Иначе их называют необходимымиусловиями того, что 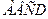— ромб.

Свойство для любого понятия можно сформулировать по следующей схеме:

Если что-то является объектом такого-то вида,

для него выполняется то-то.

Признак –это достаточное условие, т.е. такое, которое формулируется по схеме:

Если для данного объекта выполняется такое-то условие,

объект принадлежит к рассматриваемому виду.

В математике часты случаи, когда одно и то же условие является и свойством, и признаком данного понятия.

Признак: Если в четырёхугольнике диагонали пересекаются в одной точке и делятся ею пополам, то четырёхугольник является параллелограммом.

Свойство: Если четырёхугольник является параллелограммом, то его диагонали пересекаются в одной точке и делятся ею пополам.

Такое условие, которое является одновременно и признаком, и свойством, называется характеристическим свойством понятия. Сформулировать можно его двумя способами с использованием слов: или “необходимо и достаточно”, или “тогда и только тогда”.

1) Четырехугольник является параллелограммом тогда и только тогда, когда его диагонали пересекаются в одной точке и делятся ею пополам.

2) Для того чтобы четырехугольник являлся параллелограммом необходимо и достаточно, чтобы его диагонали пересекались и делились ею пополам.

IV.При изучении теоремы можно условно выделить следующие этапы:

1) подготовительный этап

I. Осуществляется актуализация знаний, необходимых для введения и доказательства теоремы.

¾ мотивация изучения теоремы:

a) обобщение необходимых в жизни фактов и явлений и перевод их на математический язык;

b) показать необходимость знания той или иной теоремы для решения практических задач;

c) показать, как решалась данная проблема в истории науки.

¾ с помощью практической работы подвести к открытию теоремы.

¾ разобраться в структуре теоремы (дано, доказать);

¾ сделать чертеж и краткую запись

III.С помощью специально подобранных заданий и вопросов осуществить:

¾ Решение простейших задач (по готовому чертежу) на непосредственное применение теоремы.

IV. Решение разнообразных задач, повторение доказательства.

1.При поиске путей доказательства следует иметь ввиду:

1) Если в доказательстве используется известный учащимся метод или доказательство осуществляется по известной уже схеме, то учащимся сообщается метод, а дальше беседа по плану:

¾ каков 1-ый шаг данного метода?

¾ Как это сделать для данной теоремы?

2) если теорема содержит небольшое число этапов доказательства, каждый из которых “прозрачно” связан с другим, то применяем аналогичные рассуждения: что нужно знать, чтобы доказать (с конца)

3) если теорема сложная, то ученикам следует сообщить идею доказательства.

2.На этапе усвоения доказательства задаем вопросы:

Источник

Структура теорем. Виды теорем. Методика изучения теорем в школьном курсе математики.

Виды теорем:

3) Из не А следует не Б. ( ) противоположное утверждение.

4) Из не Б следует не А. ( ) контрапозитивное утверждение.

Если импликация P=>Q является теоремой, то : условие P называется достаточным условием для условия Q, а условие Q – необходимым условием для условия P.

Если теоремами являются импликации P => Q и Q=> P, то каждое из условий является необходимым и достаточным для другого.

Этапы работы с теоремой в школе

Профессиональный – выполнение логико-математического анализа, выбор методов работы, отбор содержания;

Подготовительный – актуализация необходимых знаний учащихся, мотивация необходимости изучения факта;

Введение формулировки теоремы и осуществление ее доказательства- первичное усвоение факта и его доказательства учащимися;

Применение теоремы в качестве аргумента при выводе следствий.

Этапы изучения теоремы учащимися

Ознакомление с фактом, отраженным в теореме,

Усвоение содержания теоремы, ее структуры.

Ознакомление со способом доказательства,

Установление связи с другими теоремами

Методы введения теоремы

Система задач на усвоение теоремы и ее доказательства

На раскрытие необходимости знания математического факта, сформулированного в теореме;

На актуализацию фактов, используемых при доказательств и способов доказательств, аналогичных используемым для данной теоремы;

На осознание факта, сформулированного в теореме;

На усвоение формулировки;

На усвоение отдельных этапов доказательства;

На повторение хода доказательства (например, на других чертежах);

На отыскание другого способа доказательства;

На применение теоремы для получения новых математических фактов (следствий);

На применение теоремы для решения других задач на вычисление, построение и доказательства.

Виды формулировок теорем: категорическая и условная (импликативная).

Структура формулировки: условие, заключение, разъяснительная часть.

Логическая структура условия и заключения: конъюнктивная, дизъюнктивная.

Примеры

Часто в формулировках теорем используется выражение «необходимо и достаточно» (ПРИЗНАК). В логике это выражение соответствует эквиваленции, которая, как известно, представима в виде конъюнкции двух импликаций. Одна из этих импликаций выражает теорему, доказывающую НЕОБХОДИМОСТЬ признака, другая выражает теорему, доказывающую ДОСТАТОЧНОСТЬ признака. Например, признак перпендикулярности двух плоскостей:

«Для того чтобы две плоскости были перпендикулярны, НЕОБХОДИМО и ДОСТАТОЧНО, чтобы одна из них проходила через прямую, перпендикулярную к другой», может быть сформулирован и так: «Две плоскости перпендикулярны, ЕСЛИ И ТОЛЬКО ЕСЛИ одна из них проходит через прямую, перпендикулярную к другой»:

Источник

Реферат. Теорема. Виды теорем. Методика работы над теоремой

Ищем педагогов в команду «Инфоурок»

НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ДОПОЛНИТЕЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ИНСТИТУТ ДИСТАНЦИОННОГО ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

Теорема. Виды теорем. Методика работы над теоремой

слушатель _3.30.1__ курса

Крупко Елена Александровна

к. психол. наук, доц. Шелепанова Н.В.

ПРЯМЫЕ ПРИЁМЫ ДОКАЗАТЕЛЬСТВА 8

КОСВЕННЫЕ ПРИЁМЫ ПОИСКА 8

МЕТОДЫ ДОКАЗАТЕЛЬСТВА, ВЫДЕЛЕННЫЕ ПО ИСПОЛЬЗУЕМОМУ МАТЕМАТИЧЕСКОМУ АППАРАТУ 8

ЭТАПЫ ИЗУЧЕНИЯ ТЕОРЕМЫ 8

МЕТОДОЛОГИЧЕСКИЕ ПРИЁМЫ МОТИВИРОВКИ НЕОБХОДИМОСТИ ИЗУЧЕНИЯ ТЕОРЕМ 9

ЗАДАНИЯ, СПОСОБСТВУЮЩИЕ УСВОЕНИЮ ТЕОРЕМ 9

Теорема – математическое предложение, истинность которого устанавливается посредством доказательства.

Виды формулирования теоремы: импликативная и категорическая.

Условие теоремы – при каких условиях рассматривается в ней тот или иной объект.

Заключение теоремы – что об этом объекте утверждается.

Основные типы теорем:

4. Контрапозитивная (обратная противоположной).

Доказательство – рассуждение с целью обоснования истинности какого-либо утверждения.

Тезис – математическое предложение, в котором выражается главная цель доказательства. Форма выражения тезиса – суждение.

Аргументы доказательства – положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов – суждения.

Демонстрация – логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.

Метод доказательства – способ связи аргументов при переходе от условия к заключению суждения.

Методы доказательства, выделенные по тому, как строится обоснование тезиса: прямые и косвенные .

Рассмотрим, например, теорему «если четырехугольник является прямоугольником, то в нем диагонали равны». Построим предложение, обратное данному: «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником». Это ложное высказывание, в чем легко убедиться (в равнобедренной трапеции диагонали равны, но трапеция не является прямоугольником).

Рассмотрим теорему «в равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник – равнобедренный». Это истинное предложение и потому является теоремой. Ее называют теоремой, обратной данной.

Вообще, для какой бы теоремы мы ни формулировали предложение, обратное противоположному, оно всегда будет теоремой, потому что имеется следующая равносильность: ( АВ) (ВА).

Эту равносильность называют законом контрапозиции.

Теоремы АВ и ВА – взаимообратные, а АВ и – взаимопротивоположные.

1. В следующих теоремах выделим условие и заключение: а) «Для того чтобы разность двух чисел делилась на 2, достаточно, чтобы на 2 делилось уменьшаемое и вычитаемое»;

б) «Для того чтобы четырехугольник был квадратом, необходимо, чтобы хоты бы один из его углов был прямым».

Решение: а) Слово достаточно относится к предложению «уменьшаемое и вычитаемое делится на 2», следовательно, это предложение и является условием теоремы. Тогда заключение теоремы – «разность двух чисел делится на 2».

б) В данной теореме есть слово «необходимо», которое относится к предложению «чтобы четырехугольник был квадратом». Значит, это и будет условием данной теоремы. А ее заключением в таком случае будет предложение «один из углов четырехугольника прямой».

2. Сформулируем следующие теоремы в виде «если …, то …»:
а) «Перпендикуляр к одной из двух параллельных прямых также перпендикуляр к другой»; б) «Всякий параллелограмм имеет центр симметрии».

Решение: а) Выделим условие и заключение теоремы: «Перпендикуляр к одной из двух параллельных прямых» – условие, «перпендикуляр к другой» – заключение. Тогда теорема примет вид: «Если есть перпендикуляр к одной из двух параллельных прямых, то он является также перпендикуляром к другой прямой».

б) Условие теоремы – «всякий параллелограмм», заключение – «имеет центр симметрии». Нашу теорему тогда можно переформулировать следующим образом: «Если фигура параллелограмм, то она имеет центр симметрии».

3. Дана теорема: «Если в четырехугольнике две противоположные стороны равны и параллельны, то четырехугольник параллелограмм». Сформулируем предложения, являющиеся обратным, противоположным и обратно противоположным.

Решение: Выделим условие и заключение данной теоремы. Условие: «в четырехугольнике две противоположные стороны равны и параллельны». Заключение: «четырехугольник – параллелограмм».

Поменяв местами условие и заключение, получим теорему, обратную данной: «Если четырехугольник – параллелограмм, то две противоположные стороны равны и параллельны», так как данное предложение истинно.

Заменяя условие и заключение исходной теоремы их отрицаниями, получим теорему, противоположную данной: «Если в четырехугольнике две противоположные стороны не равны или не параллельны, то четырехугольник – не параллелограмм». Это предложение также истинно.

Меняя местами отрицание условия и отрицание заключения, получим истинное предложение, которое является обратно противоположной теоремой: «Если четырехугольник – не параллелограмм, то две противоположные стороны не равны или не параллельны».

ПРЯМЫЕ ПРИЁМЫ ДОКАЗАТЕЛЬСТВА

— синтетический – преобразование условия суждения;

— восходящий анализ – отыскание достаточных оснований справедливости заключения;

— нисходящий анализ – отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений;

— последовательное преобразование то условия, то заключения суждения.

КОСВЕННЫЕ ПРИЁМЫ ПОИСКА

— метод от противного – метод, при котором истинность доказываемого тезиса устанавливается посредством опровержения противоречащего ему суждения;

— разделительный метод (метод разделения условий или метод исключения) – метод, при котором тезис рассматривается как один из возможных вариантов предположений, когда все предположения опровергаются, кроме одного.

МЕТОДЫ ДОКАЗАТЕЛЬСТВА, ВЫДЕЛЕННЫЕ ПО ИСПОЛЬЗУЕМОМУ МАТЕМАТИЧЕСКОМУ АППАРАТУ

— Метод геометрических преобразований – метод, используемый как средство обоснования некоторых отношений между элементами евклидовой геометрии.

— Алгебраические методы – методы доказательства теорем с помощью уравнений, неравенств, тождественных преобразований.

— Векторный метод – метод, использующий аппарат векторной алгебры.

— Координатный метод – метод, позволяющий устанавливать переход от геометрических отношений к аналитическим.

ЭТАПЫ ИЗУЧЕНИЯ ТЕОРЕМЫ

— мотивация изучения теоремы и раскрытие ее содержания;

— работа над структурой теоремы;

— мотивация необходимости доказательства теоремы;

— построение чертежа и краткая запись содержания теоремы;

— поиск доказательства, доказательство и его запись;

МЕТОДОЛОГИЧЕСКИЕ ПРИЁМЫ МОТИВИРОВКИ НЕОБХОДИМОСТИ ИЗУЧЕНИЯ ТЕОРЕМ

1. Обобщение наблюдаемых в жизни фактов и явлений и перевод их на математический язык.

2. Показ необходимости знания той или иной теоремы для решения практических задач.

3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем.

4. Показ, как решалась данная проблема в истории науки.

ЗАДАНИЯ, СПОСОБСТВУЮЩИЕ УСВОЕНИЮ ТЕОРЕМ

1) Сформулируйте теорему.

2) Выделите условие и заключение теоремы. К каким фигурам применима теорема?

3) Сформулируйте теорему со словами «Если…то…».

4) Сформулируйте предложение, обратное теореме.

5) Воспроизведите доказательство теоремы по новому чертежу, изменив его положение и обозначение элементов.

6) Составьте план доказательства.

7) Назовите аргументы, которые использовались при доказательстве.

8) Докажите теорему другим способом.

9) Решите задачи на применение теоремы.

В отличие от других наук, в математике недопустимы эмпирические доказательства: все утверждения доказываются исключительно логическими способами. В математике важную роль играют математическая интуиция и аналогии между разными объектами и теоремами; тем не менее, все эти средства используются учёными только при поиске доказательств, сами доказательства не могут основываться на таких средствах.

Доказательства, написанные на естественных языках, могут быть не очень подробными в расчёте на то, что подготовленный читатель сам сможет восстановить детали. Строгость доказательства гарантируется тем, что его можно представить в виде записи на формальном языке (это и происходит при компьютерной проверке доказательств).

Лернер И.Я. Дидактические основы методов обучения. – М.: Педагогика, 1981. 185 с.

Саранцев Г.И. Теоретические основы методики упражнений по математике в средней школе: Автореф. дисс. … доктора пед. наук.- Л.: Изд-во Ленинградского педуниверситета, 1987. – 36 с.

Саранцев Г.И. Упражнения в обучении математике, т.4. – М.: Просвещение, 1995. – 240 с.

Источник