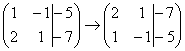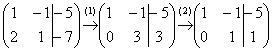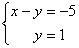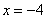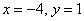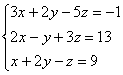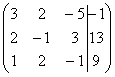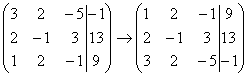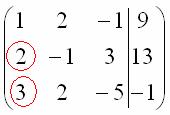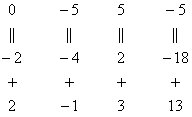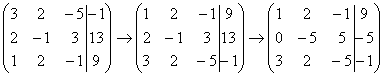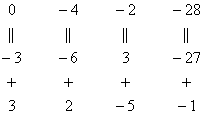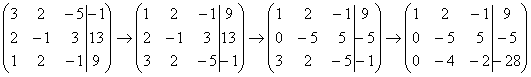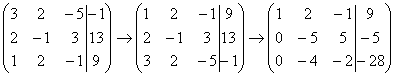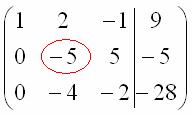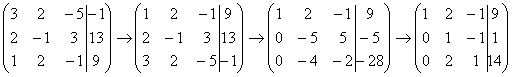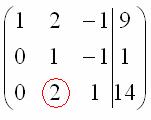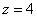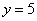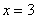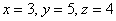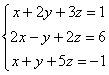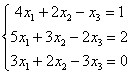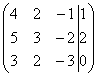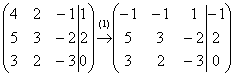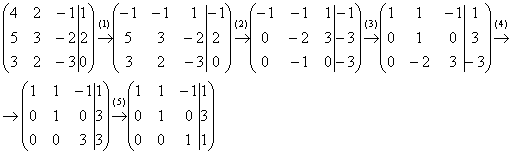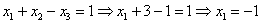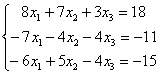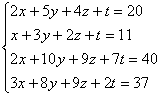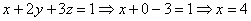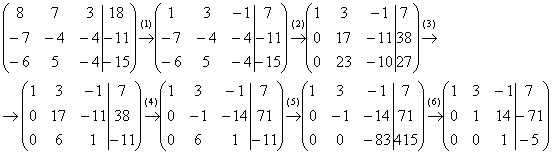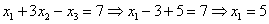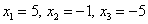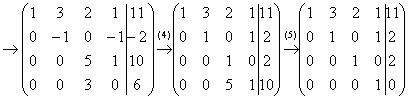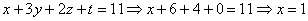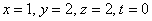на чем основан метод гаусса

Решение систем линейных уравнений методом Гаусса

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие метода Гаусса

После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.

У студентов наибольшие трудности вызывает именно прямой ход, то есть приведение исходной системы к трапециевидной. И это несмотря на то, что преобразования, которые необходимы для этого, называются элементарными. И называются неслучайно: в них требуется производить умножение (деление), сложение (вычитание) и перемену уравнений местами.

Преимущества метода:

Кроме того, метод Гаусса является основой одного из методов нахождения обратной матрицы.

Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.

Пример 1. Решить систему линейных уравнений, применяя обратный ход:

Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y:

Из предыдущих шагов выписываем решение системы уравнений:

Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.

Элементарные преобразования системы линейных уравнений

На анимации выше показано, как система уравнений постепенно превращается в трапециевидную. То есть такую, которую вы видели на самой первой анимации и сами убедились в том, что из неё просто найти значения всех неизвестных. О том, как выполнить такое превращение и, конечно, примеры, пойдёт речь далее.

При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно:

В результате преобразований получаем систему линейных уравнений, эквивалентную данной.

Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы

Пример 2. Решить методом Гаусса систему линейных уравнений

Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.

Для упрощения внешнего вида решения составим расширенную матрицу системы:

Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:

С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую строку, умноженную на (в нашем случае на ), к третьей строке – первую строку, умноженную на (в нашем случае на ).

Это возможно, так как

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x:

Для упрощения второй строки полученной системы умножим её на и получим вновь матрицу системы уравнений, эквивалентной данной системе:

Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на (в нашем случае на ).

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:

Мы получили эквивалентную данной трапециевидную систему линейных уравнений:

Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере.

Из первого уравнения найдём x:

Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан тот же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ, и это уже предмет пятой части этого урока.

Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение

Пример 3. Решить систему линейных уравнений:

Пример 4. Решить систему линейных уравнений методом Гаусса:

Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на . Получаем расширенную матрицу трапециевидной формы.

Получили систему уравнений, которой эквивалентна заданная система:

Следовательно, полученная и данная системы являются совместными и определёнными. Окончательное решение находим «с конца». Из четвёртого уравнения непосредственно можем выразить значение переменной «икс четвёртое»:

.

Это значение подставляем в третье уравнение системы и получаем

,

откуда находим «икс третье»:

.

Далее, подставляем значения и во второе уравнение системы:

,

.

Наконец, подстановка значений

в первое уравнение даёт

,

откуда находим «икс первое»:

.

Ответ: данная система уравнений имеет единственное решение .

Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан тот же ответ, если система имеет однозначное решение.

Решение методом Гаусса прикладных задач на примере задачи на сплавы

Решение. Составляем систему линейных уравнений:

Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:

Составляем расширенную матрицу системы:

Прямой ход завершился. Получили расширенную матрицу трапециевидной формы.

Применяем обратный ход. Находим решение с конца. Видим, что .

Из второго уравнения находим

,

.

Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан то же ответ, если система имеет однозначное решение.

С помощью метода Гаусса можно установить, совместна или несовместна любая система n линейных уравнений с n переменными.

Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений

После выполнения преобразований в расширенной матрице системы (перестановки строк, умножения и деления строк на некоторое число, прибавлению к одной строке другой) могли появиться строки вида

,

соответствующие уравнению вида

Если во всех уравнениях имеющих вид

свободные члены равны нулю, то это означает, что система неопределённа, то есть имеет бесконечное множество решений, а уравнения этого вида – «лишние» и их исключаем из системы.

Пример 6. Решить методом Гаусса систему линейных уравнений:

Решение. Составим расширенную матрицу системы. Затем с помощью первого уравнения исключим переменную из последующих уравнений. Для этого ко второй, третьей и четвёртой строкам прибавим первую, умноженную соответственно на :

Теперь вторую строку прибавим к третьей и четвёртой.

В результате приходим к системе

Последние два уравнения превратились в уравнения вида . Эти уравнения удовлетворяются при любых значениях неизвестных и их можно отбросить.

Чтобы удовлетворить второму уравнению, мы можем для и выбрать произвольные значения , тогда значение для определится уже однозначно: . Из первого уравнения значение для также находится однозначно: .

Как заданная, так и последняя системы совместны, но неопределённы, и формулы

при произвольных и дают нам все решения заданной системы.

Метод Гаусса и системы линейных уравнений, не имеющие решений

Как уже говорилось в связи с первым примером, после выполнения преобразований в расширенной матрице системы могли появиться строки вида

,

соответствующие уравнению вида

Если среди них есть хотя бы одно уравнение с отличным от нуля свободным членом (т.е. ), то данная система уравнений является несовместной, то есть не имеет решений и на этом её решение закончено.

Пример 7. Решить методом Гаусса систему линейных уравнений:

Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Чтобы получить целые отношения коэффициентов, поменяем местами вторую и третью строки расширенной матрицы системы.

Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на .

Заданная система эквивалентна, таким образом, следующей:

Полученная система несовместна, так как её последнее уравнение не может быть удовлетворено никакими значениями неизвестных. Следовательно, данная система не имеет решений.

Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение

Пример 8. Решить систему линейных уравнений:

Метод Гаусса и системы, в которых число неизвестных меньше числа уравнений

Пример 9. Решить методом Гаусса систему линейных уравнений:

Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Проведём подготовительные работы. Чтобы было удобнее с отношением коэффициентов, нужно получить единицу в во втором столбце второй строки. Для этого четвёртую строку умножаем на , а полученную в результате четвёртую строку меняем местами со второй строкой.

Получили следующую систему уравнений, которой эквивалентна заданная система:

и известны, а находим из первого уравнения:

.

Ответ: данная система уравнений имеет единственное решение (1; 1; 1).

Метод Гаусса и системы, в которых число неизвестных больше числа уравнений

Если при выполнении преобразований в расширенной матрице системы встретилось хотя бы одно уравнение вида

(*)

с равным нулю свободным членом, то в итоге получим эквивалентную исходной системе систему линейных уравнений, в которой число уравнений меньше числа переменных, а уравнения вида (*) удовлетворяются при любых значениях неизвестных. Их можно отбросить.

Неизвестным, которые удовлетворяли уравнению вида 0 = 0, например, третьему и четвёртому (*, отброшенным уравнениям), придадим произвольные значения (пример 2). Они чаще всего записываются так: . Подставляя эти значения в остальные уравнения, не имеющие вида (*), например, первое и второе, получаем формулы, дающие нам значения остальных неизвестных. В них можно подставлять любые численные значения и . Следовательно, существует бесконечное множество выбора значений этих неизвестных, поэтому полученная система уравнений является неопределённой. В этом случае неопределённой является и исходная система.

Пример 10. Решить методом Гаусса систему линейных уравнений:

Решение. Составляем расширенную матрицу системы. Далее ко второй строке прибавляем первую, умноженную на .

Заданная система эквивалентна, таким образом, следующей:

В ней отсутствуют уравнения, дающие однозначные значения для и . Это равносильно появлению уравнений вида , которые можно отбросить. Мы можем для и выбрать произвольные значения . Из первого уравнения значение для находится однозначно: .

Как заданная, так и последняя системы совместны, но неопределённы, и формулы

при произвольных и дают нам все решения заданной системы.

Источник

Метод Гаусса (последовательного исключения неизвестных).
Примеры решений для чайников

Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Как решить систему линейных уравнений? Далее полезно изучить урок Правило Крамера. Матричный метод.

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья Несовместные системы и системы с общим решением. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.

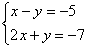
На первом этапе нужно записать расширенную матрицу системы: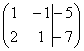
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

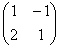
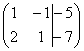
Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

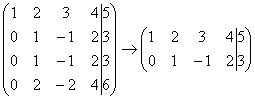
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.

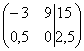
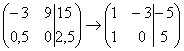
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

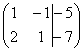
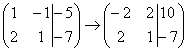
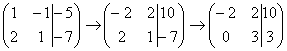
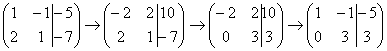
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2: . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

На практике так подробно, конечно, не расписывают, а пишут короче: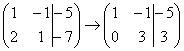

Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »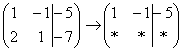

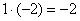
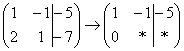
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

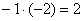
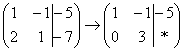
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

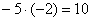
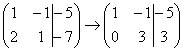
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе 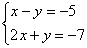. Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: 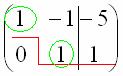. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.

В нижнем уравнении у нас уже готовый результат: .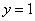

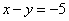
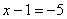
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Ответ:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: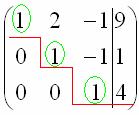

И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число: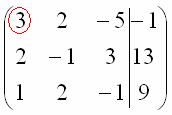

Почти всегда здесь должна находиться единица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения. Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2:

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3:

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО: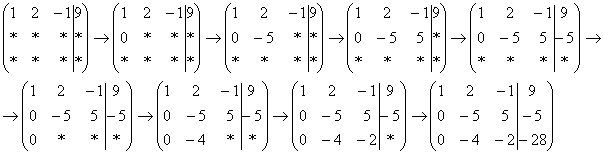

А мысленный ход самих расчётов я уже рассмотрел выше.

Далее нужно получить единицу на следующей «ступеньке»:

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2: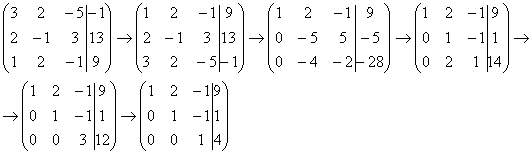

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: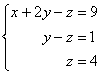

Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

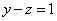
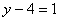
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

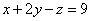
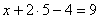
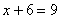
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ:

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми!

Решить систему линейных уравнений методом Гаусса

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

Дальше алгоритм работает уже по накатанной колее:

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

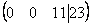
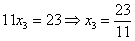
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился: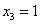

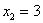
Ответ: .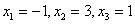

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.

В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: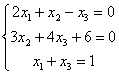

Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод. В расширенной матрице системы на месте отсутствующих переменных ставим нули: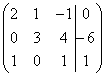

Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .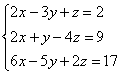

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример: 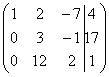. Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном. Поэтому для всех желающих более сложный пример для самостоятельного решения:

Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Пример 2: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.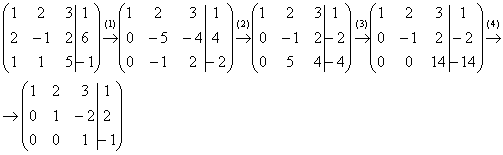

Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание, что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход: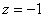

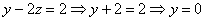
Ответ: .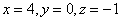

Пример 4: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы

Обратный ход: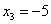

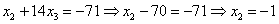
Ответ:

Пример 5: Решение: Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: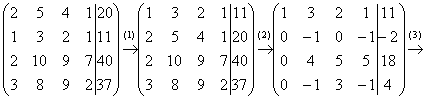

Выполненные преобразования:
(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.

Обратный ход: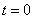

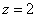
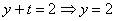
Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник