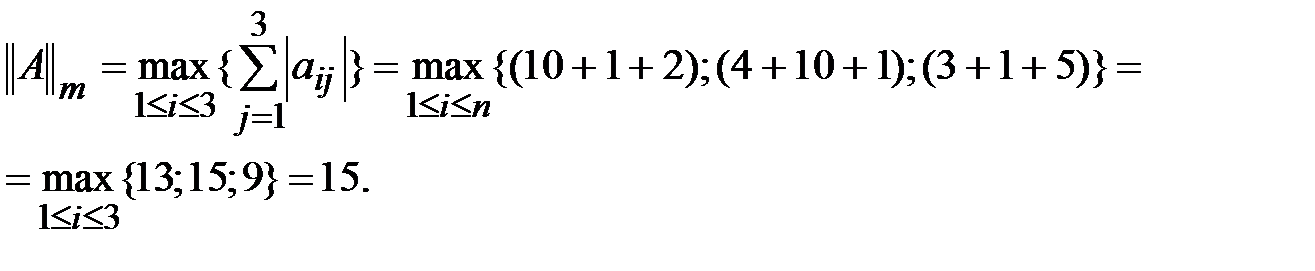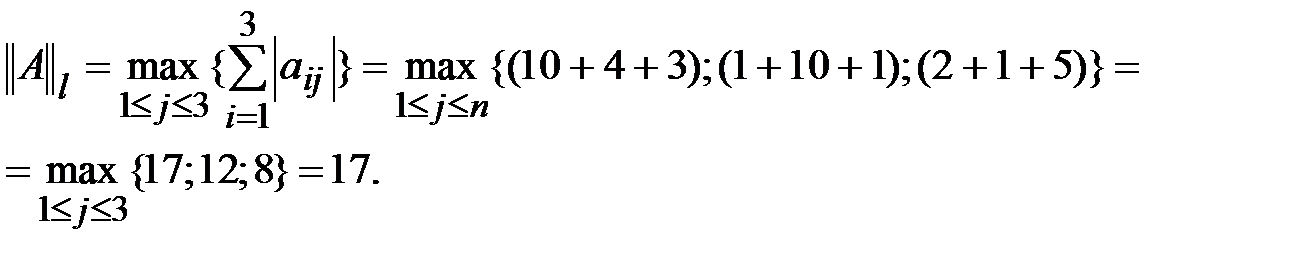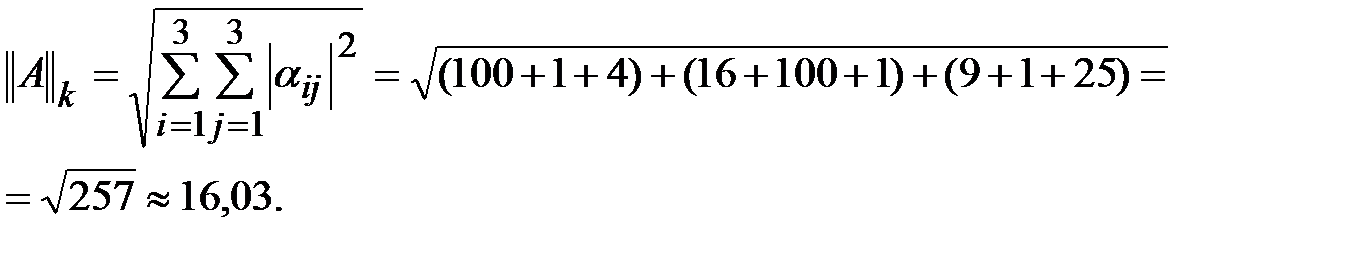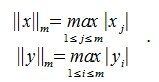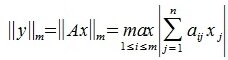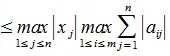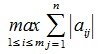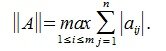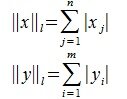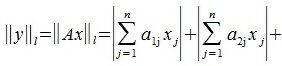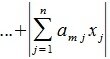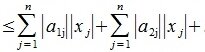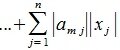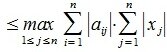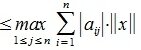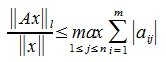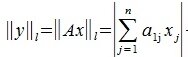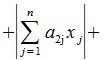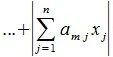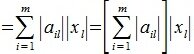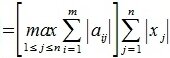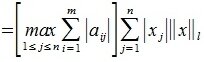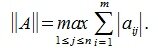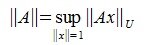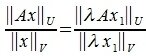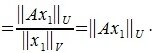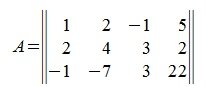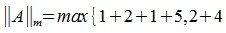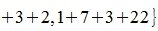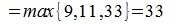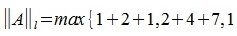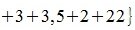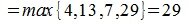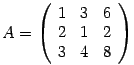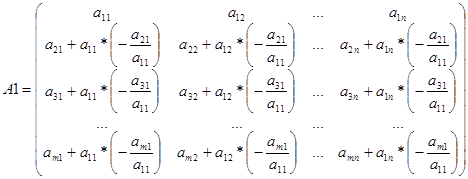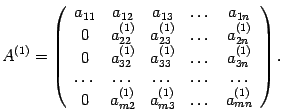Что такое норма матрицы

Как вычислить норму матрицы

Нормы матриц часто используются при определении погрешности различных численных методов. В частности, в итерационных методах решения систем линейных алгебраических уравнений они применяются для того, чтобы определить погрешность решения, найденного на каждой итерации.

Как правило, используются нормы трех видов.

1) M-норма. Вычисляется по формуле

, где i – номер строки, j – номер столбца.

Пример.Для матрицы 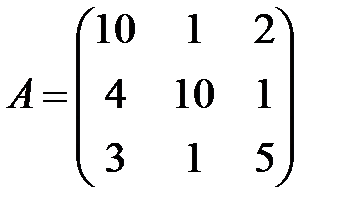m-норма равна

2) L-норма. Вычисляется по формуле

, где i – номер строки, j – номер столбца.

Пример.Для матрицы l-норма равна

3) K-норма. Вычисляется по формуле

, где i – номер строки, j – номер столбца.

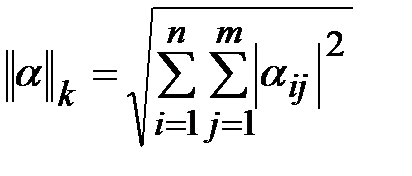
Пример.Для матрицы

k-норма равна

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8444 – | 7337 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Определим норму матрицы A равенством:

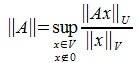(1)

Из определения нормы матрицы следует:

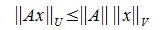(2)

Пусть для двух матриц A и B порядка m×n определены одни и те же векторные нормы. Тогда имеем соотношение:

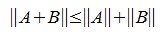(3)

Кроме того справедливо равенство

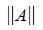
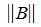
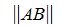
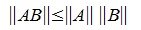
Пусть для m×n матрицы A и n×k матрицы B определены матричные нормы , и пусть для m×k матрицы AB определена норма . Тогда

.

1. Пусть в пространствах V и U введена векторная норма

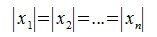
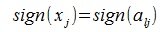
В (5) и (6) неравнетство превращается в равенство, если взять и , j=1. n, где l-то значение i, при котором

достигает своего максимума. Учитывая высшеизложенное, неравенство (6) и равенство (1), получим:

2. Введем в пространствах V и U векторную норму

Пусть 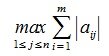достигается при j=l. Для вектора x, у которого только один элемент отлично от нуля, имеем:

Учитывая (1),(8) и (9) получим l-норму матрицы A:

Норму матрицы, определяемую с помощью формулы (1), называется операторной нормой, подчиненной данной норме векторов.

Отметим, что определение нормы матрицы (1) эквивалентно следующему определению:

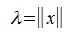
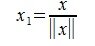
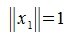
Действительно, любой ненулевой вектор x∈V можно представить в виде произведения λx₁, где , . Тогда, учитывая, что , получим:

Примеры вычисления нормы матрицы

Вычислим m-норму и l-норму матрицы используя (7) и (10).

Геометрическая интерпретация нормы матрицы

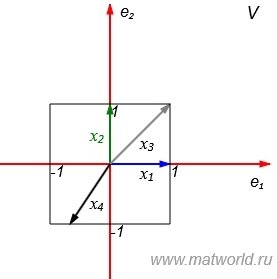
Пусть в линейном пространстве V введена m-норма для всех векторов x∈V:

.

Найдем норму матрицы

.

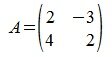
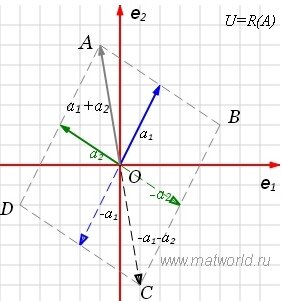
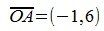
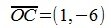
На рисунке рис. 2 изображено пространство столбцов матрицы A. Каждому вектору x∈X соответствует вектор Ax в U. Конечные точки этих векторов находятся на пунктирном четырехугольнике ABCD. m-норма матрицы A – это модуль наибольшго координата наибольшего из векторов, конечная точка которого находится на четырехугольнике ABCD. На рис.2 это векторы и а модуль наибольшего координата 6. Используя (3), аналитически получим тот же результат.

Отметим, что норма матрицы показывает насколько максимально растягивается вектор x при отображении y=Ax. В нашем примере векторы х растягиваются максимально 6 раз.

Программированию нельзя научить, можно только научится

Главная » Уроки по Численным методам » Урок 12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц

Если все миноры матрицы Aпорядка kравны нулю, то все миноры порядка k+1, если такие существуют, тоже равны нулю.
Рангом матрицы A называется наибольший из порядков миноров матрицы A, отличных от нуля.
Максимум ранг может быть равен минимальному числу из количества строк или столбцов матрицы, т.е. если матрица имеет размер 4х5, то максимум ранг будет 4.
Минимум ранг матрицы равен 1, если только вы не имеете дело с нулевой матрицей, там всегда ранг равен нулю.

Ранг невырожденной квадратной матрицы порядка n равен n, так как ее определитель является минором порядка n и у невырожденной матрицы отличен от нуля.
При транспонировании матрицы ее ранг не меняется.

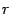
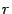
Пусть ранг матрицы равен . Тогда любой минор порядка , отличный от нуля, называется базисным минором.
Пример. Дана матрица А.

Определитель матрицы 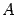равен нулю.
Минор второго порядка 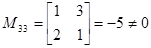. Следовательно, r(A)=2 и минор базисный.
Базисным минором является также минор .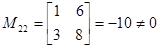
Минор 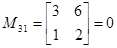, т.к. =0, поэтому не будет базисным.
Задание: самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.

Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.

Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.

При элементарных преобразованиях ранг матрицы не меняется.
Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.

Пусть требуется вычислить ранг матрицы 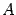размеров mxn.

В результате расчетов матрица А1 имеет вид

В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.
Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.

В лабораторно-практической работе рассмотрим пример нахождения ранга матрицы.

Рисунок 10.

Вторая норма матрицы представляет из себя квадратный корень из суммы квадратов всех элементов матрицы. А это значит мы возводим в квадрат все элементы матрицы, затем складываем полученные значения и из результата извлекаем квадратный корень.
В нашем случае, 2 норма матрицы получилась равна квадратному корню из 269. На схеме, я приближенно извлекла квадратный корень из 269 и в результате получила приблизительно около 16,401. Хотя более правильно не извлекать корень.

Источник

Норма матрицы

Определим норму матрицы A равенством:

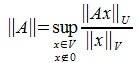(1)

Из определения нормы матрицы следует:

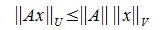(2)

Пусть для двух матриц A и B порядка m×n определены одни и те же векторные нормы. Тогда имеем соотношение:

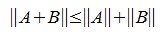(3)

Кроме того справедливо равенство

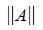
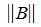
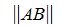
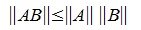
Пусть для m×n матрицы A и n×k матрицы B определены матричные нормы , и пусть для m×k матрицы AB определена норма . Тогда

.

1. Пусть в пространствах V и U введена векторная норма

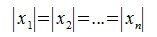
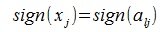
В (5) и (6) неравнетство превращается в равенство, если взять и , j=1. n, где l-то значение i, при котором

достигает своего максимума. Учитывая высшеизложенное, неравенство (6) и равенство (1), получим:

2. Введем в пространствах V и U векторную норму

Пусть 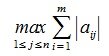достигается при j=l. Для вектора x, у которого только один элемент отлично от нуля, имеем:

Учитывая (1),(8) и (9) получим l-норму матрицы A:

Норму матрицы, определяемую с помощью формулы (1), называется операторной нормой, подчиненной данной норме векторов.

Отметим, что определение нормы матрицы (1) эквивалентно следующему определению:

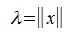
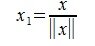
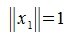
Действительно, любой ненулевой вектор x∈V можно представить в виде произведения λx₁, где , . Тогда, учитывая, что , получим:

Примеры вычисления нормы матрицы

Вычислим m-норму и l-норму матрицы используя (7) и (10).

Геометрическая интерпретация нормы матрицы

Пусть в линейном пространстве V введена m-норма для всех векторов x∈V:

.

Найдем норму матрицы

.

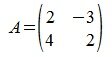
Рассмотрим множество всех векторов, которые имеют норму 1. В двухмерном пространстве это те векторы конечные точки которых находятся на квадрате на рис. 1. Обозначим это множество символом X₀.

Отметим, что норма матрицы показывает насколько максимально растягивается вектор x при отображении y=Ax. В нашем примере векторы х растягиваются максимально 6 раз.

Источник

Численные методы линейной алгебры

Основные положения численного анализа

Классическим средством изучения математических моделей и исследований на их основе свойств реальных объектов являются аналитические методы, позволяющие получать точные решения в виде математических формул. Эти методы дают наиболее полную информацию о решении задачи, и они до настоящего времени не утратили своего значения. Однако, к сожалению, класс задач, для которого они могут использоваться, весьма ограничен. Поэтому решение, как правило, осуществляется численными методами.

В численном анализе используются два класса численных методов:

Решения, получаемые численными методами, в силу их приближенности содержат некоторые погрешности. Рассмотрим их источники и типы.

Один из типов погрешностей обусловлен неадекватностью выбранной математической модели исходной физической. Эта неадекватность в большей или меньшей степени присуща всем приближенно решаемым задачам. Данная погрешность является неустранимой. Неточность (неопределенность) задания исходных данных приводит также к неустранимым погрешностям.

Дадим некоторые понятия из теории погрешностей вычислительных действий над приближенными величинами.

Пусть [math]x[/math] — точное, но, как правило, неизвестное значение некоторой величины, а [math]\widehat[/math] — ее известное приближенное значение.

Абсолютной погрешностью приближения [math]\widehat[/math] называется разность [math]\Delta=\bigl|x-\widehat\bigr|[/math] (в общем случае [math]\Delta\widehat[/math] имеет размерность величины [math]x[/math] ).

Относительная погрешность приближения [math]\widehat[/math] обозначается [math]\delta[/math] и выражается отношением [math]\delta= \frac<\Delta\widehat><|\widehat|>[/math] ( [math]\delta[/math] — безразмерная величина, [math]\widehat\ne0[/math] ). Часто величина [math]\delta[/math] вычисляется в процентах, и тогда она умножается на сто.

Такие погрешности оцениваются при рассмотрении численных методов. Эти оценки могут производиться до выполнения вычислений ( априорные оценки ) и после них ( апостериорные оценки ).

Как правило, численный алгоритм решения задачи завершается, если погрешность меньше заданной заранее величины.

Норма матриц: понятие, определение, примеры

2. [math]\|\alpha x\|=|\alpha|\cdot\|x\|[/math] для любого действительного числа [math]\alpha[/math] ;

Аксиома 3 называется неравенством треугольника.

Примером нормы матрицы-столбца может быть семейство норм

где при любом целом положительном [math]p[/math] определяется функция, удовлетворяющая условиям 1-3.

Приведем часто используемые нормы матриц-столбцов.

1. [math]\|x\|_1=\max_>|x_i|[/math] — максимум среди модулей элементов столбца;

2. [math]\textstyle<\|x\|_2=\sum\limits_^|x_i|>[/math] — сумма модулей элементов столбца;

3. [math]\textstyle<\|x\|_3=\sqrt<\sum\limits_^x_i^2>>[/math] — квадратный корень из суммы квадратов элементов.

1. Можно показать, что справедливы следующие соотношения

2. Норма может быть использована при анализе сходимости последовательностей матриц-столбцов.

2) [math]\|\alpha\cdot A\|=|\alpha|\cdot\|A\|[/math] для любого действительного числа [math]\alpha[/math] ;

3) [math]\|A+B\|\leqslant\|A\|+\|B\|[/math] для любых двух матриц [math]A[/math] и [math]B[/math] размеров [math](m\times n)[/math] (неравенство треугольника);

4) [math]\|A\cdot B\|\leqslant\|A\|\cdot\|B\|[/math] для любых двух матриц, у которых определено произведение.

Наиболее употребительными являются следующие формулы для вычисления значений норм матриц с действительными элементами.

1) [math]\textstyle<\|A\|_1= \max\limits_<1\leqslant i\leqslant m>\sum\limits_^|a_|>[/math] — максимум суммы модулей элементов в строке;

2) [math]\textstyle<\|A\|_2= \max\limits_<1\leqslant j\leqslant n>\sum\limits_^|a_|>[/math] максимум суммы модулей элементов в столбце;

3) [math]\|A\|_3=\sqrt<\lambda_<\max>(A^TA)>[/math] — квадратный корень из максимального собственного значения [math]\lambda_i[/math] матрицы [math]A^TA[/math] ;

4) [math]\textstyle<\|A\|_4= \sqrt<\sum\limits_^ \sum\limits_^ a_^2>>[/math] — квадратный корень из суммы квадратов элементов.

Заметим, что вычисление нормы [math]\|A\|_3= \sqrt<\lambda_<\max>(A^TA)>[/math] связано с весьма трудоемкими операциями. Поскольку справедливо неравенство

Отметим некоторые свойства предела матриц. Если [math]\lim_A^<(k)>=A,

где считается, что все операции определены.

Источник