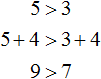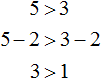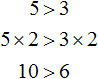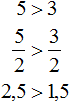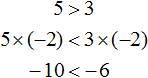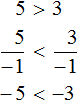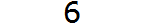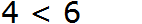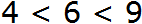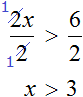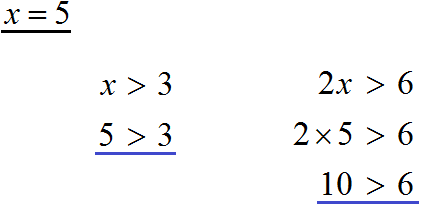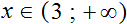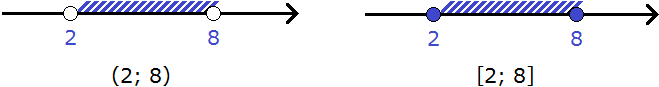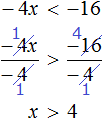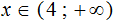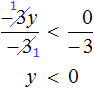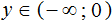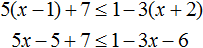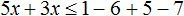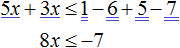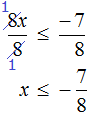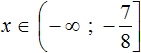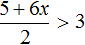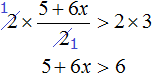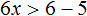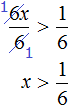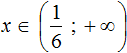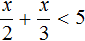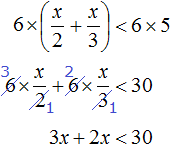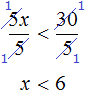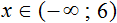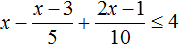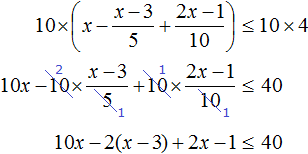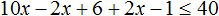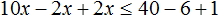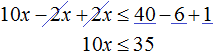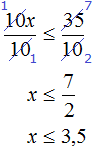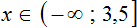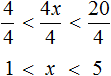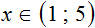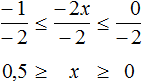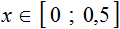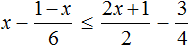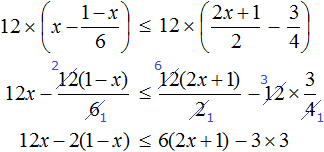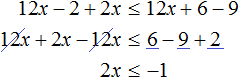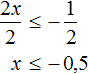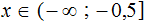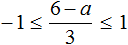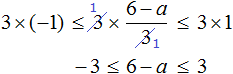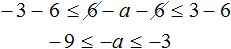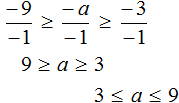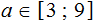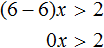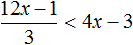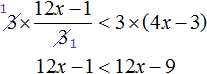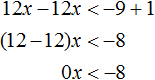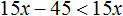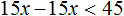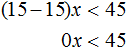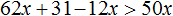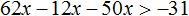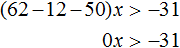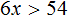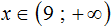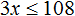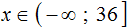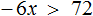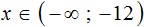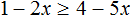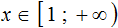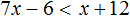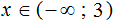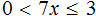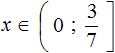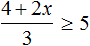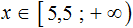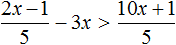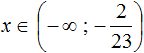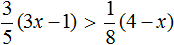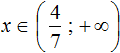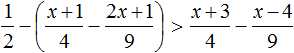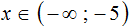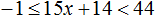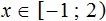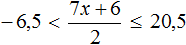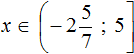Что такое неверное неравенство

Понятие неравенства, связанные определения.

Обратной стороной равенства выступает неравенство. В этой статье мы введем понятие неравенства, и дадим начальную информацию о них в контексте математики.

Сначала разберем, что такое неравенство, введем понятия не равно, больше, меньше. Дальше поговорим о записи неравенств с помощью знаков не равно, меньше, больше, меньше или равно, больше или равно. После этого затронем основные типы неравенств, дадим определения строгих и нестрогих, верных и неверных неравенств. Дальше мимоходом перечислим основные свойства неравенств. Наконец, остановимся на двойных, тройных и т.д. неравенствах, и разберем, какой смысл они несут в себе.

Навигация по странице.

Что такое неравенство?

Понятие неравенства, как и понятие равенства, связано со сравнением двух объектов. И если равенство характеризуется словом «одинаковые», то неравенство, напротив, говорит о различии сравниваемых объектов. Например, объекты и — одинаковые, про них можно сказать, что они равные. А вот два объекта и отличаются, то есть, они не равны или неравные.

Неравенство сравниваемых объектов познается вместе со смыслом таких слов, как выше, ниже (неравенство по высоте), толще, тоньше (неравенство по толщине), дальше, ближе (неравенство по удаленности от чего-либо), длиннее, короче (неравенство по длине), тяжелее, легче (неравенство по весу), ярче, тусклее (неравенство по яркости), теплее, холоднее и т.п.

Как мы уже отмечали при знакомстве с равенствами, можно говорить как о равенстве двух объектов в целом, так и о равенстве их некоторых характеристик. Это же относится и к неравенствам. В качестве примера приведем два объекта и . Очевидно, они не одинаковые, то есть, в целом они неравные. Они не равны по размеру, также они не равны по цвету, однако, можно говорить о равенстве их форм – они оба являются кругами.

В математике общий смысл неравенства сохраняется. Но в ее контексте речь идет о неравенстве математических объектов: чисел, значений выражений, значений каких-либо величин (длин, весов, площадей, температур и т.п.), фигур, векторов и т.п.

Не равно, больше, меньше

Иногда ценность представляет именно сам факт неравенства двух объектов. А когда сравниваются значения каких-либо величин, то, выяснив их неравенство, обычно идут дальше, и выясняют, какая величина больше, а какая – меньше.

Смысл слов «больше» и «меньше» мы познаем практически с первых дней нашей жизни. На интуитивном уровне мы воспринимаем понятие больше и меньше в плане размера, количества и т.п. А дальше постепенно начинаем осознавать, что при этом фактически речь идет о сравнении чисел, отвечающим количеству некоторых предметов или значениям некоторых величин. То есть, в этих случаях мы выясняем, какое из чисел больше, а какое – меньше.

Запись неравенств с помощью знаков

Также широко в ходу знак больше или равно вида ≥, а также знак меньше или равно ≤. Подробнее об их смысле и назначении поговорим в следующем пункте.

Еще заметим, что алгебраические записи со знаками не равно, меньше, больше, меньше или равно, больше или равно, аналогичные рассмотренным выше, называют неравенствами. Более того, имеет место определение неравенств в смысле вида их записи:

Источник

Что такое числовые выражения, равенства, неравенства и уравнения

Выражение

Числовое выражение — это числа, соединённые знаками арифметических действий: сложение, вычитание, умножение и деление.

Найти значение числового выражения — это значит выполнить все указанные арифметические действия и получить конкретное число.

Кроме арифметических действий выражения могут содержать скобки, которые влияют на порядок действий при решении выражения.

Пример 1:

Равенство

Равенства — это числа или выражения, соединённые знаком = (равно).

Равенство считается верным, если числа или числовые выражения слева и справа от знака =, имеют равное значение.

Равенство считается неверным, если числа или числовые выражения слева и справа от знака =, не равны (≠).

При решении равенств соблюдается следующий порядок действий:

Пример 2:

1) 5 = 7 — равенство неверно, так как 5 ≠ 7.

2) 36 : 2 = 6 • 3 — равенство верно, так как:

3) 48 + 9 = 54 — 1 — равенство неверно, так как:

Неравенство

Пример 3:

1) 5 > 7 — неравенство неверно, так как 5

3) 4 + 5 • 6 > (4 + 5) • 6 — неравенство неверно, так как:

Уравнение

Уравнение — это равенство, которое содержит неизвестное число, обозначенное какой-либо латинской буквой: x, y, a, b, z, d и т.д.

Корень уравнения — это число, при подставлении котрого вместо буквы в равенство делает это равенство верным.

Решить уравнение — это значит найти все возможные корни уравнения.

Порядок и правила решения уравнений зависят от того, к какому типу они относятся:

Источник

Понятие неравенства, связанные определения

Неравенство – обратная сторона равенства. Материал данной статьи дает определение неравенства и начальную информацию о нем в разрезе математики.

Определение неравенства

Понятие неравенства, как и понятие равенства, связывается с моментом сравнения двух объектов. В то время как равенство означает «одинаковы», то неравенство, напротив, свидетельствует о различиях объектов, которые сравниваются. К примеру, и — одинаковые объекты или равные. и — объекты, отличающиеся друг от друга или неравные.

Неравенство объектов определяется по смысловой нагрузке такими словами, как выше – ниже (неравенство по признаку высоты); толще – тоньше (неравенство по признаку толщины); длиннее – короче (неравенство по признаку длины) и так далее.

Возможно рассуждать как о равенстве-неравенстве объектов в целом, так и о сравнении их отдельных характеристик. Допустим, заданы два объекта: и . Без сомнений, эти объекты не являются одинаковыми, т.е. в целом они не равны: по признаку размера и цвета. Но, в то же время, мы можем утверждать, что равны их формы – оба объекта являются кругами.

В контексте математики смысловая нагрузка неравенства сохраняется. Однако, в этом случае речь идет о неравенстве математических объектов: чисел, значений выражений, значений величин (длина, площадь и т.д.), векторов, фигур и т.п.

Не равно, больше, меньше

В зависимости от целей поставленной задачи ценным можем являться уже просто факт выяснения неравенства объектов, но обычно вслед за установлением факта неравенства происходит выяснение того, какая все же величина больше, а какая – меньше.

Значение слов «больше» и «меньше» нам интуитивно знакомо с самого начала нашей жизни. Очевидным является навык определять превосходство объекта по размеру, количеству и т.д. Но в конечном счете любое сравнение приводит нас к сравнению чисел, которые определяют некоторые характеристики сравниваемых объектов. По сути, мы выясняем, какое число больше, а какое – меньше.

Утром температура воздуха составила 10 градусов по Цельсию; в два часа дня этот показатель составил 15 градусов. На основе сравнения натуральных чисел мы можем утверждать, что значение температуры утром было меньше, чем ее значение в два часа дня (или в два часа дня температура увеличилась, стала больше, чем была температура утром).

Запись неравенств с помощью знаков

Существуют общепринятые обозначения для записи неравенств:

Подробнее их смысл разберем ниже. Дадим определение неравенств по виду их записи.

Строгие и нестрогие неравенства

Знаки строгих неравенств – это знаки «больше» и «меньше»: > и Неравенства, составленные с их помощью – строгие неравенства.

Верные и неверные неравенства

Верное неравенство – то неравенство, которое соответствует указанному выше смыслу неравенства. В ином случае оно является неверным.

Приведем простые примеры для наглядности:

Неравенство 5 ≠ 5 является неверным, поскольку на самом деле числа 5 и 5 равны.

Или такое сравнение:

Аналогичными по смыслу термину «верное неравенство» являются фразы «справедливое неравенство», «имеет место неравенство» и т.д.

Свойства неравенств

Опишем свойства неравенств. Очевидный факт, что объект никак не может быть неравным самому себе, и это есть первое свойство неравенства. Второе свойство звучит так: если первый объект не равен второму, то и второй не равен первому.

Опишем свойства, соответствующие знакам «больше» или «меньше»:

Знакам нестрогих неравенств также присущи некоторые свойства:

Двойные, тройные и т.п. неравенства

Источник

Верные и неверные равенства и неравенства

Презентация к уроку

Планируемые результаты (универсальные учебные действия).

(96) Неявное сравнение. Выделение существенных признаков понятий “верное равенство”, “неверное равенство”.

(97) Составление новых объектов (свободное конструирование). Нахождение значений выражений.

(94) Сравнение текстов с целью подведения под понятие “задача”. Решение задачи.

1. Организационный момент.

Долгожданный дан звонок,
Начинается урок!
Начинаем мы опять:
Решать, отгадывать, считать!
Пожелаем всем удачи –
За работу, в добрый час!

Встанем, повернёмся, наклоном головы поприветствуем наших гостей.

Введение в тему урока.

Учитель.

— Ребята, чтобы в очередной раз нам попасть в страну математика, мы должны отгадать загадку:

Стоит трёхглавый великан
Он правила расскажет нам,
Кому куда идти и ехать,
Чтоб не создать затор, помехи.
Если загорелся красный,
Стой! Движение опасно!
Загорелся жёлтый свет,
Ожидай, движенья нет!
Свет зелёный на табло,
Движение разрешено.
— Что это? ( Светофор).

-Светофор задаёт вопрос: На какой свет разрешено переходить дорогу?

— Переходим, когда загорается зелёный свет, дорогу переходим аккуратно, особенно в зимний период. Зимой на дорогах очень скользко.

— Но загорелся красный свет, светофор не пропускает нас в страну математика, он хочет проверить, как мы знаем таблицу сложения, как мы умеем считать устно. Давайте покажем светофору. Готовы? Да.

2. Актуализация знаний. Повторение пройденного материала.

— В стране математика на небе появились тучки, они мешают нам познакомиться с новыми жителями страны. Чтобы их разогнать, нужно выполнить задание – найти значения выражений, а поможет вам знание таблицы сложения. Готовы? Да.

— Посмотрите ребята на доску, кто нас встречает в стране математика? Как называются эти знаки? (больше, меньше, равно)

— Как мы называем математические записи с такими знаками? (РАВЕНСТВА И НЕРАВЕНСТВА)

— Так какую математическую запись называем равенством или неравенством? (Математическую запись, в которой есть знаки = называем равенством или неравенством).

— Ребята, посмотрите, загорелся зелёный свет, мы верно выполнили задание, правильно ответили на вопросы. Смело отправляемся в страну математика.

— Все ваши умения пригодятся сегодня на уроке, а внимание – особенно. Скажите, какое сегодня число? ( 25 февраля)

— Вспомним всё, что знаем о числах 2 и 5.Какие это числа – однозначные или двузначные?

– Это числа однозначные, т.к. при их записи используется одна цифра.

— Какие это числа: натуральные или ненатуральные?

– Эти числа натуральные, т.к. стоят в натуральном ряду чисел.

— О каком числе мы говорим, что оно ненатуральное? Почему?

— Число 0 ненатуральное число. Число ноль ничего не обозначает.

— Правильно. В переводе с латинского слово “нулус” означало ничто, а в Древней Индии отсутствие чего-либо обозначали пустым кругом.

— Какие числа являются предшествующими для чисел 2 и 5? (1 и 4)

— Какие следующие за числами 2 и 5. (3 и 6)

— Какое из этих чисел (2 и 5) больше, и на сколько? (3)

— Как узнал? Как узнать на сколько одно число больше или меньше другого?

(Чтобы узнать, насколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее.)

— Пропишем числа “в воздухе”.

— Молодцы! Закрываю презентацию, открываю доску.

– Запишем сначала предшествующие числа в соседних клеточках 1 4, запишем следующие числа 3 6 в соседних клеточках (показываю указкой всё на доске).

— Кому трудно, можно поработать фломастером на волшебной страничке.

— Запишите все числа, которые встретились нам в чистописании в порядке возрастания, на новой строчке, через клеточку.

— Что у вас получилось? Прочитай (Учитель записывает на доске). Можем мы назвать эту запись натуральным рядом чисел? Нет, почему? 0 – не натуральное число.

— Пойти к доске, составить с числами 2 и 5 равенства и неравенства. Где нужно вставь число два, где нужно, число 5!

— Какую математическую запись мы называем равенством или неравенством?

— Почему записи на доске мы не можем назвать выражением? Что такое выражение?

— Правильно. Выражение – запись, в которой числа соединены знаками действий. Знаков сравнения в выражениях нет. Садись, молодец.

ЗАКРЫВАЮ ДОСКУ, ОТКРЫВАЮ ПРЕЗЕНТАЦИЮ

Работа над новым материалом. Проблема: Неявное сравнение.

-Ребята, внимание на доску. Сегодня в страну математика с нами отправились Саша и Катя. Посмотрите на задания, которые они выполняли. Как называются такие математические записи?

— Равенства и неравенства.

— Верно, мы видим знаки сравнения. Прочитайте задание.

— Хочу обратить ваше внимание, вам было сделано предупреждение ещё в начале урока, чтобы вы были предельно внимательными. Катя и Саша выполняли ОДИНАКОВЫЕ задания, но знаки сравнения (показываю указкой на доске) в первой и второй строчках у них разные. Значения выражений не совпадают. Почему так произошло?

— Исправьте у себя на листочках Катину ошибку.

— Вторая строчка, кто допустил ошибку? (Ошибку допустил Саша, 8-5=3, а 3 больше двух)

— Исправим. Проверим. Слайд.

— Третья строчка, кто допустил ошибку? Ошибку допустила Катя. 7-2=5, а 5 больше четырёх на один. Исправим. Проверим. Слайд.

— Четвёртая строка – ошибку допустил Саша. 4+4=8, а 8 больше 7. Проверим.

— Посмотрите внимательно, что у нас получилось. Равенства и неравенства у нас остались? (да)

— Но какие-то из них верные, а какие-то нет! Выпишите в тетрадь ВЕРНЫЕ равенства и ВЕРНЫЕ неравенства – т.е. те, в которых ребята не допустили ошибок.

3. САМОСТОЯТЕЛЬНАЯ РАБОТА в тетрадях

СЛАЙД с выполненным заданием.

— Встаньте те, у кого запись совпадает с записью на доске. Какие равенства и неравенства вы выписывали? Верные.

— Без ошибок, без несоответствий, то есть ВЕРНЫЕ! А почему не записали остальные равенства и неравенства? Там есть ошибки.

— Т.е. мы не выписывали те, которые ребята выполнили неверно!

— Верные мы выписали, неверные нет (показываю на доске). Так какие бывают равенства и неравенства?

Вывод: Равенства и неравенства бывают верные и неверные.

— Правильно. Равенства и неравенства без ошибок, без несоответствий называют ВЕРНЫМИ, а равенства и неравенства, где левая часть не соответствует правой (или её значение), о таких неравенствах говорят, что это неравенства неверные.

Вы молодцы, вы хорошо поработали, давайте отдохнём.

4. ФИЗМИНУТКА (СЛАЙД).

5. Закрепление материала. Работа по учебнику:

— Ребята откройте учебники на странице 38, найдите номер 94 ( Сравнение текстов с целью подведения под понятие “задача”. Решение задачи.).

— Сравните тексты. Какой из них является задачей? Вспомним, какой текст мы называем задачей?

— Текст, в котором есть условие, вопрос, числовые данные для ответа на него, мы называем задачей.

— Так какой из текстов является задачей, докажи?

— Второй текст является задачей, так как в нём есть вопрос, есть числовые данные для ответа на него.

— Прочитай вслух ещё раз ЗАДАЧУ. (СЛАЙД С ЗАДАЧЕЙ)

— О чём говорится в задаче? (О игрушках на полке – куклах и мишках).

ЧИТАЕТ УЧЕНИК: Сколько игрушек на полке?

— Сможем ли мы ответить на вопрос в задаче? (да)

— Докажи. Что мы должны знать, чтобы ответить на вопрос в задаче?

(Количество мишек, количество кукол)

— Известно сколько плюшевых мишек стояло на полке? (да, 3)

— Известно сколько кукол стояло на полке? (да, 3)

— Нас просят решить задачу, записав выражение. После найти его значение.

— Какое действие запишем в выражении, чтобы узнать, сколько всего игрушек стояло на полке? (действие сложения)

— Выйди к доске и запиши выражение, с помощью которого мы ответим на вопрос в задаче.

ЗАКРЫВАЮ ПРЕЗЕНТАЦИЮ, ОТКРЫВАЮ ДОСКУ

ВЫХОД УЧЕНИКА К ДОСКЕ

— Эти числа обозначают количество мишек и количество кукол. Складываем эти числа. Действие сложения записываем с помощью знака +.

— Найдите значение этого выражения: 3+3=6.

— Что обозначает число 6? (количество всех игрушек, сколько игрушек всего)

— Давайте проверим себя, правильно ли мы ответили на вопрос в задаче – пересчитаем все игрушки на рисунке. Поставили пальчики в учебник – считаем. Мы решили верно. 6=6

— Запиши на доску, а вы ребята в тетрадь это равенство: 6=6.

— Ребята, посмотрите внимательно на нашу запись – там, где записано решение задачи. Мы записали выражение, нашли его значение, что у нас получилось? Как называется такая математическая запись? РАВЕНСТВО

— Какое это равенство? ВЕРНОЕ РАВЕНСТВО

ЗАКРЫВАЮ ДОСКУ И ОТКРЫВАЮ ПРЕЗЕНТАЦИЮ: 3+3=6

— Поменяйте значение выражения так, чтобы получилось неверное равенство. Перечислите свои неверные равенства ( дети называют с мест).

— Поменяйте знак сравнения так, чтобы получилось верное неравенство. Назовите своё неравенство. Сверим с доской:

— Так какие бывают равенства и неравенства? (Полный ответ: равенства и неравенства бывают верные и неверные.)

— Там, где есть несоответствия между сравниваемыми записями слева и справа, мы говорим о неверном сравнении – неверных равенствах и неравенствах.

— В нашей стране математика давно закончился дождь. А после дождя, что мы обычно видим на небе? Красивую радугу. Если будете внимательно следить за жителем страны Математика – Котёнком Квадратиком – глазками – вы увидите красивую радугу.

6. ФИЗМИНУТКА для глаз.

7. Составление новых объектов, свободное конструирование.

— Найдите в учебнике номер 97. СЛАЙД

— Кроме млекопитающих животных на рисунке изображены насекомые и птицы. Относим ли мы их к царству животных или мы их относим к царству растений или грибов?

— Да, мы их относим к царству животных. Значит все объекты на рисунке – это животные.

Читаю по учебнику задание: запиши столько сумм, сколько на рисунке животных обитающих в воде. Запиши столько разностей, сколько животных обитающих на суше. Мы разделимся, задание будем выполнять по вариантам.

— Первый вариант запишет столько сумм, сколько на рисунке животных, обитающих в воде. Второй вариант запишет столько разностей, сколько животных, обитающих на суше. Хочу обратить ваше внимание на животное – гусь. Где он может находиться? И в воде, и на суше. Значит и первый, и второй вариант будут его учитывать.

— Давайте определим, сколько животных, обитающих в воде?

Первый вариант?(4) Перечисли – МОРЖ, ДЕЛЬФИН, КИТ, ГУСЬ. Проверим! Слайд.

— Давайте определим, сколько животных, обитающих на суше? Второй вариант?(5) Перечисли – БЕЛКА, БАБОЧКА, ГУСЬ, ЁЖИК, ОСА. Проверим! Слайд.

— Следовательно первый вариант самостоятельно записывать 4 суммы, не находя их значение. Второй – 5 разностей, не вычисляя их. Помните, что вы записываете выражения, не находя их значений. Найдите на листочках номер 97 – подписан. Вставьте в окошки нужные числа, любые.

8. Оценка и самооценка.

— Обменяйтесь листочками, проверьте, правильно ли выполнил задание ваш сосед по парте. Найдите значения выражений вашего соседа, запишите их простым карандашом. Обменяйтесь, проверьте. Можно стереть ластиком, записать свой вариант ответа, если нашли ошибку.

— Прочитаем, что у вас получилось. Первый вариант. Второй вариант.

— Ребята, вы записали выражения, нашли их значения, что у вас получилось, как мы называем такие математические записи? РАВЕНСТВА

— Равенства, в которых мы не допустили ошибок, какие они – верные или неверные? ВЕРНЫЕ.

— Надеюсь, что неверных равенств у нас в этом задании нет, или если есть, то очень мало. Листочки вложите в тетрадь, а я проверю, как справились с заданием.

9. Итог урока: Вывод. Самооценка универсальных учебных умений, действий. Презентация.

— Ребята, какие математические записи называем равенством и неравенством? Записи, в которых есть знаки сравнения, называем равенствами и неравенствами.

— Какие бывают равенства и неравенства? Равенства и неравенства бывают верными и неверными.

— Какие равенства и неравенства называем неверными? Это математические записи, где знаки сравнения поставлены неверно.

— Ребята, у вас на партах у каждого есть по два билета. Вам нужно выбрать и один из них взять в руки. Возьмите в руки цветной билет, если вы поняли, что такое верные и неверные равенства и неравенства. С этим билетом вы можете смело дальше путешествовать по стране Математика. Если вы не поняли, как различить верные и неверные равенства и неравенства, возьмите в руки черно-белый билет. С этим билетом на следующих уроках математики нужно быть внимательнее. Поднимите, покажите, все ли у нас с билетами. Молодцы! Урок закончен, идите отдыхать.

Источник

Общие сведения о неравенствах

Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.

Определения и свойства

Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, 5 > 3

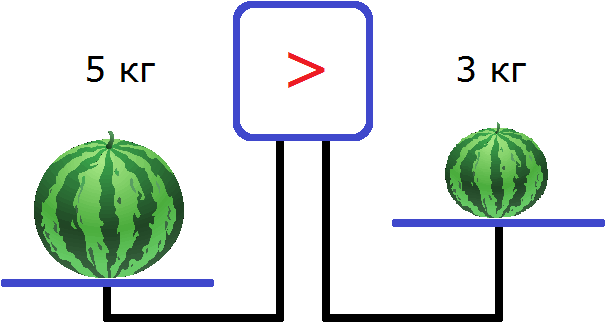
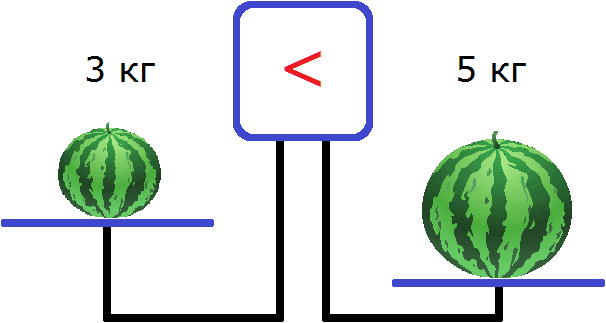
Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.

Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:

Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.

Свойство 1.

Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.

Например, прибавим к обеим частям неравенства число 4. Тогда получим:

Видим, что левая часть по-прежнему больше правой.

Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2

Видим, что левая часть по-прежнему больше правой.

Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.

Видим, что левая часть по-прежнему больше правой.

Свойство 2.

Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.

Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:

Видим, что левая часть по-прежнему больше правой.

Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2

Видим, что левая часть по-прежнему больше правой.

Свойство 3.

Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.

Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1

Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.

Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.

Неравенство 8 не является верным, поскольку не выполняется условие «8 меньше, чем 6».

Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:

Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.

Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.

Строгие и нестрогие неравенства

Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:

Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.

Двойное неравенство

Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.

Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.

Сначала записываем 6

Слева записываем, что это число больше, чем число 4

Справа записываем, что число 6 меньше, чем число 9

Неравенство с переменной

Неравенство, как и равенство может содержать переменную.

Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.

Значение переменной, при котором неравенство становится верным, называется решением неравенства.

Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.

Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:

Как решать неравенства

Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.

Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.

А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.

Пример 1. Решить неравенство 2x > 6

Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.

В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.

Итак, разделим обе части неравенства на 2.

Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.

Отметим, что неравенство x > 3 является строгим. « Переменная x строго больше трёх».

Видим, что в обоих случаях получается верное неравенство.

После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:

Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.

Числовые промежутки

Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.

Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8

Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.

Границы могут принадлежать числовому промежутку либо не принадлежать ему.

Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.

Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.

На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.

Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:

В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.

На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.

Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.

Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.

На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:

На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.

На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.

С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:

То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.

Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:

В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.

А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.

Существуют разновидности числовых промежутков. Рассмотрим каждый из них.

Числовой луч

Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее

Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.

На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:

Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.

Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.

Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3

Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.

Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:

В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.

Открытый числовой луч

Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.

На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:

Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.

Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:

На письме открытый числовой луч, заданный неравенством x , обозначается следующим образом:

Запишем ответ к неравенству x с помощью обозначения открытого числового луча:

В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x Граница 2 не принадлежит множеству решений, поскольку неравенство x является строгим.

Отрезок

Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:

На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:

Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему. Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:

Интервал

Изобразим интервал на координатной прямой:

На письме интервал, заданный неравенством a обозначается следующим образом:

Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 с помощью этого обозначения:

Полуинтервал

Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.

В ситуации с полуинтервалом a ≤ x ему (полуинтервалу) принадлежит левая граница.

А в ситуации с полуинтервалом a ему принадлежит правая граница.

Изобразим полуинтервал 2 ≤ x на координатной прямой:

Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x принадлежит множеству его решений.

А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x не принадлежит множеству его решений.

На письме полуинтервал, заданный неравенством a ≤ x обозначается следующим образом:

Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x с помощью этого обозначения:

Изобразим полуинтервал 2 на координатной прямой:

Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 не принадлежит множеству его решений.

А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 принадлежит множеству его решений.

Изображение числовых промежутков на координатной прямой

Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок). В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.

Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5

Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:

Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой

Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.

Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.

Символ +∞ указывает, что нас интересуют все числа, которые больше 5. Соответственно, вся область справа от границы 5 выделяется штрихами:

Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.

Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:

Пример 4. Изобразить числовой промежуток, заданный неравенством −5

Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.

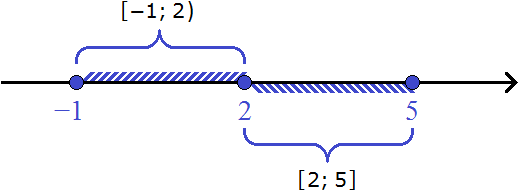
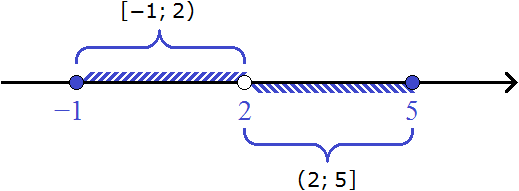
Пример 5. Изобразить на координатной прямой числовые промежутки [−1; 2) и [2; 5]

В этот раз изобразим на координатной прямой сразу два промежутка. Промежуток [−1; 2) является полуинтервалом, промежуток [2; 5] — отрезком.

У полуинтервала [−1; 2) левая граница принадлежит ему, а правая нет.

А у отрезка [2; 5] обе границы принадлежат ему.

Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]

Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.

В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.

А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.

Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:

Примеры решения неравенств

Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax ), будем называть линейным неравенством с одной переменной.

Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2

Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b

Пример 1. Решить неравенство x − 7

Прибавим к обеим частям неравенства число 7

Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x и обозначается как ( −∞ ; a)

На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:

Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4

Получилось верное числовое неравенство. Значит решение верное.

Пример 2. Решить неравенство −4x

Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:

Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 3. Решить неравенство 3y + 1 > 1 + 6y

Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:

Приведём подобные слагаемые:

Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:

Решениями неравенства y являются все числа, меньшие нуля. Изобразим множество решений неравенства y на координатной прямой и запишем ответ в виде числового промежутка:

Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)

Раскроем скобки в обеих частях неравенства:

Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:

Приведем подобные слагаемые:

Разделим обе части получившегося неравенства на 8

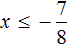
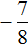
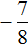
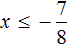
Решениями неравенства являются все числа, которые меньше . Граница принадлежит множеству решений, поскольку неравенство является нестрогим.

Изобразим множество решений неравенства 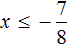на координатной прямой и запишем ответ в виде числового промежутка:

Пример 5. Решить неравенство

Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:

Теперь перенесем 5 из левой части в правую часть, изменив знак:

Изобразим множество решений неравенства 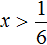на координатной прямой и запишем ответ в виде числового промежутка:

Пример 6. Решить неравенство

Умножим обе части на 6

Решениями неравенства x являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x строгим.

Изобразим множество решений неравенства x на координатной прямой и запишем ответ в виде числового промежутка:

Пример 7. Решить неравенство

Умножим обе части неравенства на 10

В получившемся неравенстве раскроем скобки в левой части:

Перенесем члены без x в правую часть

Приведем подобные слагаемые в обеих частях:

Разделим обе части получившегося неравенства на 10

Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5. Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.

Изобразим множество решений неравенства x ≤ 3,5 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 8. Решить неравенство 4

Чтобы решить такое неравенство, нужно переменную x освободить от коэффициента 4. Тогда мы сможем сказать в каком промежутке находится решение данного неравенства.

Чтобы освободить переменную x от коэффициента, можно разделить член 4x на 4. Но правило в неравенствах таково, что если мы делим член неравенства на какое-нибудь число, то тоже самое надо сделать и с остальными членами, входящими в данное неравенство. В нашем случае на 4 нужно разделить все три члена неравенства 4

Решениями неравенства 1 являются все числа, которые больше 1 и меньше 5. Границы 1 и 5 не принадлежат множеству решений, поскольку неравенство 1 является строгим.

Изобразим множество решений неравенства 1 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 9. Решить неравенство −1 ≤ −2x ≤ 0

Разделим все члены неравенства на −2

Решениями неравенства 0 ≤ x ≤ 0,5 являются все числа, которые больше 0 и меньше 0,5. Границы 0 и 0,5 принадлежат множеству решений, поскольку неравенство 0 ≤ x ≤ 0,5 является нестрогим.

Изобразим множество решений неравенства 0 ≤ x ≤ 0,5 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 10. Решить неравенство

Умножим обе неравенства на 12

Раскроем скобки в получившемся неравенстве и приведем подобные слагаемые:

Разделим обе части получившегося неравенства на 2

Решениями неравенства x ≤ −0,5 являются все числа, которые меньше −0,5. Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.

Изобразим множество решений неравенства x ≤ −0,5 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 11. Решить неравенство

Умножим все части неравенства на 3

Теперь из каждой части получившегося неравенства вычтем 6

Каждую часть получившегося неравенства разделим на −1. Не забываем, что при делении всех частей неравенства на отрицательное число, знак неравенства меняется на противоположный:

Решениями неравенства 3 ≤ a ≤ 9 являются все числа, которые больше 3 и меньше 9. Границы 3 и 9 принадлежат множеству решений, поскольку неравенство 3 ≤ a ≤ 9 является нестрогим.

Изобразим множество решений неравенства 3 ≤ a ≤ 9 на координатной прямой и запишем ответ в виде числового промежутка:

Когда решений нет

Для наилучшего понимания, перепишем приведение подобных слагаемых в левой части следующим образом:

Пример 2. Решить неравенство

Умножим обе части неравенства на 3

В получившемся неравенстве перенесем член 12x из правой части в левую часть, изменив знак. Затем приведём подобные слагаемые:

Правая часть получившегося неравенства при любом x будет равна нулю. А ноль не меньше, чем −8. Значит неравенство 0x не имеет решений.

Ответ: решений нет.

Когда решений бесконечно много

Пример 1. Решить неравенство 5(3x − 9)

Раскроем скобки в правой части неравенства:

Перенесём 15x из правой части в левую часть, изменив знак:

Приведем подобные слагаемые в левой части:

А если приведённое равносильное неравенство 0x имеет бесчисленное множество решений, то и исходное неравенство 5(3x − 9) имеет те же решения.

Ответ можно записать в виде числового промежутка:

В этом выражении говорится, что решениями неравенства 5(3x − 9) являются все числа от минус бесконечности до плюс бесконечности.

Пример 2. Решить неравенство: 31(2x + 1) − 12x > 50x

Раскроем скобки в левой части неравенства:

Перенесём 50x из правой части в левую часть, изменив знак. А член 31 из левой части перенесём в правую часть, опять же изменив знак:

Приведём подобные слагаемые:

А если приведённое равносильное неравенство 0x > −31 имеет бесчисленное множество решений, то и исходное неравенство 31(2x + 1) − 12x > 50x имеет те же решения.

Запишем ответ в виде числового промежутка:

Задания для самостоятельного решения

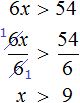
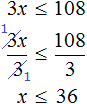
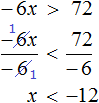
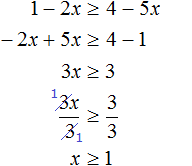
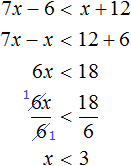
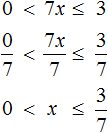
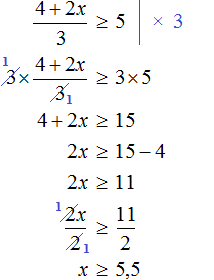
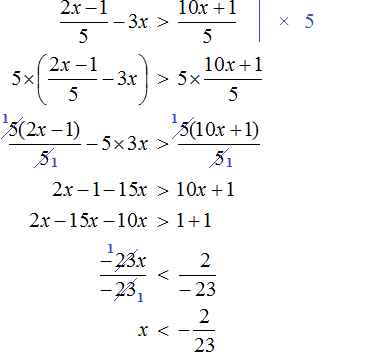
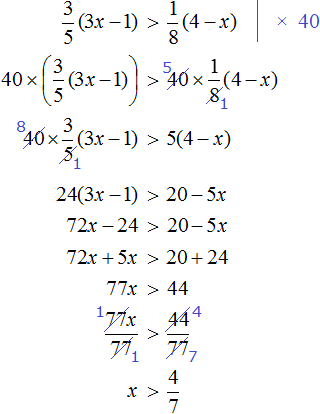
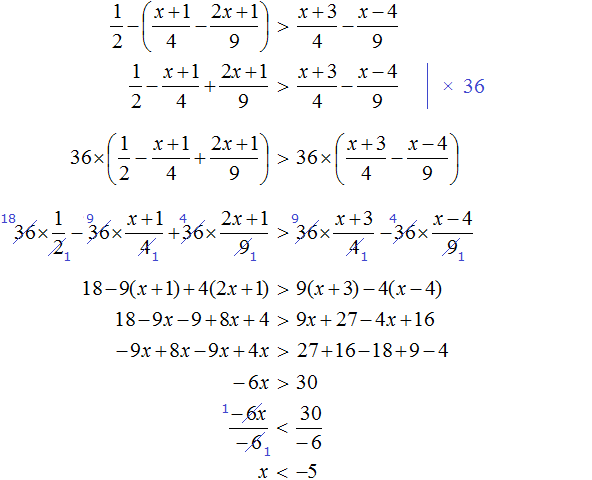
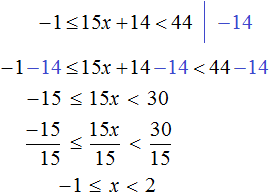
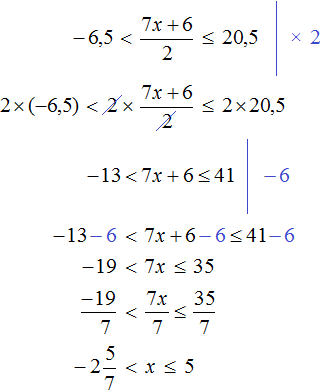
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник