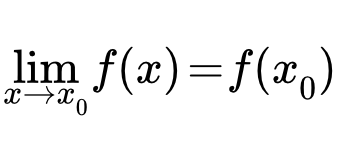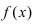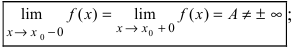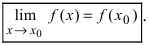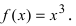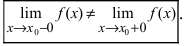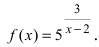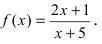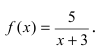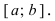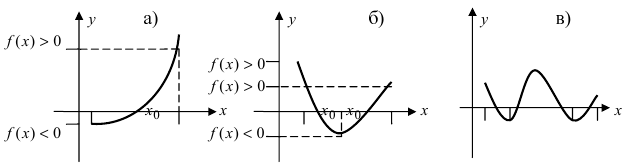Что такое непрерывность в математике
Непрерывность функций – теоремы и свойства
Определение непрерывности функции
Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x 0 , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x 0 равен значению функции в x 0 :
.
Свойства непрерывных в точке функций
Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.
Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».
Непрерывность сложной функции
Предел сложной функции
Точки разрыва
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Свойства функций, непрерывных на отрезке
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.
Обратные функции
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Свойства и непрерывность элементарных функций
Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.
Показательная функция
Логарифм
Экспонента и натуральный логарифм
Степенная функция
Тригонометрические функции
Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус ( sin x ), косинус ( cos x ), тангенс ( tg x ) и котангенс ( ctg x ), непрерывны на своих областях определения.
Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус ( arcsin x ), арккосинус ( arccos x ), арктангенс ( arctg x ) и арккотангенс ( arcctg x ), непрерывны на своих областях определения.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Непрерывность (математика)
Исторически определенное для функций действительной переменной, понятие непрерывности обобщается на функции между метрическими пространствами или между топологическими пространствами в локальной форме и в глобальной форме.
Резюме
Определение реальных функций
Функция f называется непрерывной по a, если:
Комментарий
Примеры
Характеристики
Понятие непрерывности на интервале вещественных функций
Комбинация непрерывных функций является непрерывной функцией. Соединение непрерывной функции и сходящейся последовательности является сходящейся последовательностью.
Ошибки, которых следует избегать
Определение в случае метрических пространств
Определение
Мы говорим, что отображение f непрерывно в точке a, если:
Примеры
Общее определение (топологические пространства)
Местное определение
Мы можем сделать так, чтобы локальное определение (то есть точки) непрерывности опиралось на понятие предела :
Функция f называется непрерывной в точке a, если f ( a ) является пределом функции f в этой точке.
Глобальные характеристики
Мы можем вывести из локального определения три эквивалентные характеристики приложений, которые являются непрерывными (в любой точке исходного пространства).
Связь с интуитивным понятием заключается в следующем: когда функция «прыгает», это означает, что точки, очень близкие к исходному пространству, обнаруживаются на очень удаленных точках по прибытии. Однако для непрерывного приложения эти скачки невозможны, потому что, если мы рассмотрим начальную точку и ее изображение по прибытии, мы знаем, что вся окрестность этой начальной точки должна прибыть в окрестности точки прибытия. [не ясно]
Примеры
Эквивалентность метрического и топологического определения
Концепция преемственности в истории
Преемственность не всегда определялась прежним образом.
Эйлер в своем Introductio in analysin infinitorum определяет непрерывную функцию как функцию, определяемую одним конечным или бесконечным аналитическим выражением ( целым рядом ), и называет прерывными или смешанными функциями те, которые имеют несколько аналитических выражений в зависимости от интервалов. Сильвестр Лакруа (1810) называет непрерывной функцией функцию, все значения которой определяются одним и тем же законом или зависят от одного и того же уравнения. Это понятие непрерывности называется эйлеровой непрерывностью и является более строгим, чем нынешнее определение. Например, функция, определенная для любого отрицательного действительного числа как f ( x ) = x и любого положительного действительного числа как f ( x ) = x 2, является непрерывной в текущем смысле и смешанной (разрывной) в смысле Эйлера.
Непрерывность функций и точки разрыва с примерами решения
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
— предел функции в точке 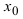
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 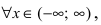
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 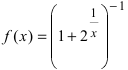
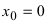
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 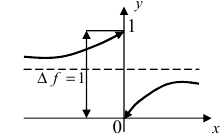
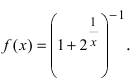
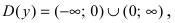
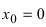
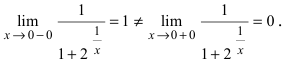
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция 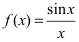
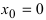
Решение:
В точке 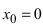
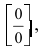
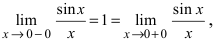
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 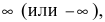
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 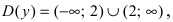
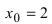
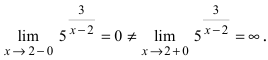
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 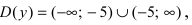
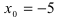
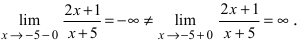
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 
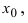
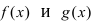
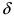
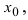
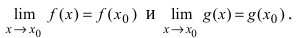
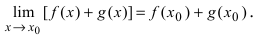
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 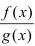
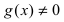
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 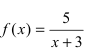
Из рисунка видно, что график функции 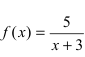
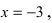
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 
Определение: Замкнутый интервал 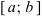
Приведем без доказательства свойства непрерывных функций на сегменте 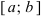
Теорема: Если функция 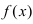
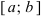
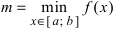
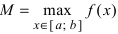
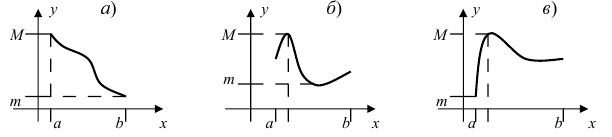
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 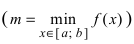
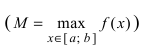
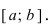
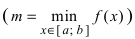
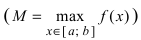
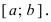
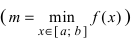
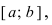
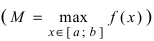
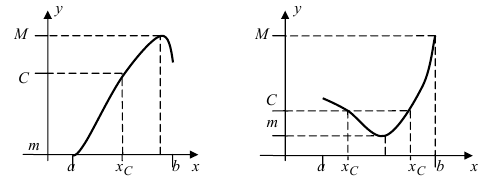
Тб. Если функция 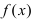
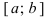
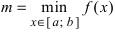
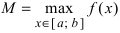
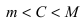
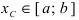
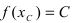
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 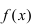
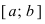
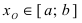
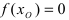
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
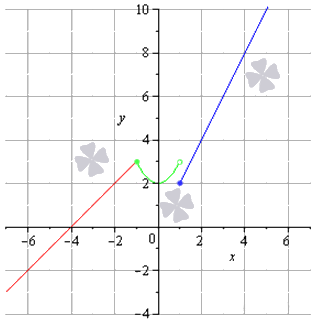
Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
Решение
Соответствующая последовательность значений функций выглядит так:
на чертеже они обозначены зеленым цветом.
Соответствующая последовательность функций:
на рисунке обозначена синим цветом.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
Устранимый разрыв первого рода
Решение
Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Решение
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
Ответ: в конечном счете мы получили:
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Решение
Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:
Ей соответствует последовательность значений функции:
Непрерывность
Полезное
Смотреть что такое «Непрерывность» в других словарях:
непрерывность — непрерывность … Орфографический словарь-справочник
Непрерывность — способность системы функционировать с заданными рабочими характеристиками в течение определенного периода. Примечание. Непрерывность характеризуется соответствующей вероятностью. Источник … Словарь-справочник терминов нормативно-технической документации
непрерывность — беспрерывность, непрестанность, беспрестанность, непрерывность; континуум, ежеминутность, постоянность, неизменность, неустанность, нескончаемость, сплошность, безустанность, перманентность, неумолчность, безостановочность, постоянство. Ant.… … Словарь синонимов
НЕПРЕРЫВНОСТЬ — неразрывная связь в бытии или переход в становлении. Всеобщность лейбницевского «закона непрерывности» (природа не делает скачков), согласно которому в природе нет никаких перерывов, пробелов и все связано благодаря переходам, была опровергнута… … Философская энциклопедия
непрерывность — Способность системы функционировать без перерывов в обслуживании с заданными рабочими характеристиками. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002]… … Справочник технического переводчика
НЕПРЕРЫВНОСТЬ — НЕПРЕРЫВНОСТЬ, непрерывности, мн. нет, жен. отвлеч. сущ. к непрерывный. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
непрерывность — НЕПРЕРШЫВНЫЙ, ая, ое; вен, вна. Не имеющий перерывов, промежутков. Н. поток. Н. стаж работы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
НЕПРЕРЫВНОСТЬ — (continuity) Отсутствие внезапных скачков функции. Функция у=f(x) является непрерывной, если при изменении значения х на сколь угодно малую величину не происходит внезапных изменений значения у. Некоторые функции непрерывны при всех значениях х,… … Экономический словарь
Непрерывность — [continuity] общее понятие математики и кибернетики, не имеющее, по видимому, общепринятого определения. В математике непрерывная функция та, значения которой близки, если близки значения аргументов. Для кибернетики здесь важно, что при… … Экономико-математический словарь
Непрерывность — (в рекламе) стратегия и тактика, используемые для составления графика рекламирования на все время рекламной кампании … Реклама и полиграфия
Непрерывность — В математике Непрерывная функция Непрерывное множество Непрерывное отображение Непрерывность (философия) Непрерывность (юридическая) действующий принцип, согласно которому судебное заседание по каждому делу происходит непрерывно, кроме времени,… … Википедия