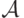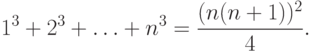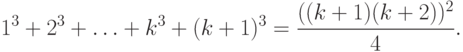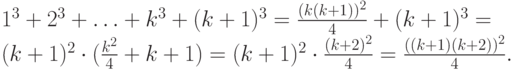Что такое метод математической индукции

Метод математической индукции для чайников

Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.

Основы метода математической индукции

Доказательство с помощью метода математической индукции проводится в два этапа:

Метод математической индукции применяется в разных типах задач:

Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.

Математическая индукция: задачи и решения

Доказательство кратности и делимости

$$a_n = 2n^3+3n^2+7n, \quad b=6.$$

Доказательство равенств и неравенств

Задача 5. Доказать равенство

Задача 6. Доказать методом математической индукции:

Задача 7. Доказать неравенство:

Задача 8. Доказать утверждение методом математической индукции:

Задача 9. Доказать неравенство:

Вычисление сумм

Задача 11. Доказать методом математической индукции:

Задача 12. Найдите сумму

Заказать решение

Полезные ссылки о ММИ

Кратенький видеоурок о ММИ

Источник

Метод математической индукции

В первом пункте мы разберем основные понятия, потом рассмотрим основы самого метода, а затем расскажем, как с его помощью доказывать равенства и неравенства.

Понятия индукции и дедукции

Для начала рассмотрим, что такое вообще индукция и дедукция.

Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному.

В целом можно сказать, что с помощью индуктивных рассуждений можно получить множество выводов из одного известного или очевидного рассуждения. Математическая индукция позволяет нам определить, насколько справедливы эти выводы.

В чем заключается метод математической индукции

В основе этого метода лежит одноименный принцип. Он формулируется так:

Применение метода математической индукции осуществляется в 3 этапа:

Как применять метод математической индукции при решении неравенств и уравнений

Возьмем пример, о котором мы говорили ранее.

Решение

Как мы уже знаем, для применения метода математической индукции надо выполнить три последовательных действия.

Мы можем представить k + 1 в качестве суммы первых членов исходной последовательности и k + 1 :

S k + 1 = S k + 1 k + 1 ( k + 2 )

Теперь выполняем нужные преобразования. Нам потребуется выполнить приведение дроби к общему знаменателю, приведение подобных слагаемых, применить формулу сокращенного умножения и сократить то, что получилось:

S k + 1 = S k + 1 k + 1 ( k + 2 ) = k k + 1 + 1 k + 1 ( k + 2 ) = = k ( k + 2 ) + 1 k + 1 ( k + 2 ) = k 2 + 2 k + 1 k + 1 ( k + 2 ) = ( k + 1 ) 2 k + 1 ( k + 2 ) = k + 1 k + 2

Таким образом, мы доказали равенство в третьем пункте, выполнив все три шага метода математической индукции.

Ответ: предположение о формуле S n = n n + 1 является верным.

Возьмем более сложную задачу с тригонометрическими функциями.

Решение

cos 2 1 = cos 2 α sin 2 1 + 1 α 2 1 sin 2 α = sin 4 α 2 sin 2 α = 2 sin 2 α · cos 2 α 2 sin 2 α = cos 2 α

Согласно тригонометрической формуле,

Ответ: На этом тождество можно считать доказанным. Мы успешно применили для этого метод математической индукции. Точно так же мы можем доказать справедливость формулы бинома Ньютона.

Пример решения задачи на доказательство неравенства с применением этого метода мы привели в статье о методе наименьших квадратов. Прочтите тот пункт, в котором выводятся формулы для нахождения коэффициентов аппроксимации.

Источник

math4school.ru

Метод математической индукции

Немного теории

Индукция есть метод получения общего утверждения из частных наблюдений. В случае, когда математическое утверждение касается конечного числа объектов, его можно доказать, проверяя для каждого объекта. Например, утверждение: «Каждое двузначное чётное число является суммой двух простых чисел,» – следует из серии равенств, которые вполне реально установить:

Метод доказательства, при котором проверяется утверждение для конечного числа случаев, исчерпывающих все возможности, называют полной индукцией. Этот метод применим сравнительно редко, поскольку математические утверждения касаются, как правило, не конечных, а бесконечных множеств объектов. Например, доказанное выше полной индукцией утверждение о четных двузначных числах является лишь частным случаем теоремы: «Любое четное число является суммой двух простых чисел». Эта теорема до сих пор ни доказана, ни опровергнута.

Математическая индукция – метод доказательства некоторого утверждения для любого натурального n основанный на принципе математической индукции: «Если утверждение верно для n=1 и из справедливости его для n=k вытекает справедливость этого утверждения для n=k+1, то оно верно для всех n». Способ доказательства методом математической индукции заключается в следующем:

1) база индукции: доказывают или непосредственно проверяют справедливость утверждения для n=1 (иногда n=0 или n=n₀);

2) индукционный шаг (переход): предполагают справедливость утверждения для некоторого натурального n=k и, исходя из этого предположения, доказывают справедливость утверждения для n=k+1.

Задачи с решениями

Проведём доказательство методом математической индукции.

База индукции. Если n=1, то А(1)=3 3 +2 3 =35 и, очевидно, делится на 7.

Предположение индукции. Пусть А(k) делится на 7.

Индукционный переход. Докажем, что А(k+1) делится на 7, то есть справедливость утверждения задачи при n=k.

А(k+1)=3 2(k+1)+1 +2 (k+1)+2 =3 2k+1 ·3 2 +2 k+2 ·2 1 =3 2k+1 ·9+2 k+2 ·2=

Последнее число делится на 7, так как представляет собой разность двух целых чисел, делящихся на 7. Следовательно, 3 2n+1 +2 n+2 делится на 7 при любом натуральном n.

Введём обозначение: а_i=2 3 i +1.

а_k+1=2 3 k+1 +1=(2 3 k ) 3 +1=(2 3 k +1)( 2 3 k ·2 –2 3 k +1)=3 k+1 ·m·((2 3 k +1) 2 –3·2 3 k )=3 k+1 ·m·((3 k+1 ·m) 2 –3·2 3 k )=

=3 k+2 ·m·(3 2k+1 ·m 2 –2 3 k ).

Следовательно, утверждение доказано для любого натурального n.

3. Известно, что х+1/x – целое число. Доказать, что х n +1/х n – так же целое число при любом целом n.

Введём обозначение: а_i=х i +1/х i и сразу отметим, что а_i=а_–i, поэтому дальше будем вести речь о натуральных индексах.

Заметим: а₁ – целое число по условию; а₂ – целое, так как а₂=(а₁) 2 –2; а₀=2.

Предположим, что а_k целое при любом натуральном k не превосходящем n. Тогда а₁·а_n – целое число, но а₁·а_n=а_n+1+а_n–1 и а_n+1=а₁·а_n–а_n–1. Однако, а_n–1, согласно индукционному предположению, – целое. Значит, целым является и а_n+1. Следовательно, х n +1/х n – целое число при любом целом n, что и требовалось доказать.

4. Доказать, что при любом натуральном n большем 1 справедливо двойное неравенство

Воспользуемся методом математической индукции.

При n=2 неравенство верно. Действительно,

Если неравенство верно при n=k, то при n=k+1 имеем

Неравенство доказано для любого натурального n > 1.

6. На плоскости дано n окружностей. Доказать, что при любом расположении этих окружностей образуемую ими карту можно правильно раскрасить двумя красками.

Воспользуемся методом математической индукции.

При n=1 утверждение очевидно.

Предположим, что утверждение справедливо для любой карты, образованной n окружностями, и пусть на плоскости задано n+1 окружностей. Удалив одну из этих окружностей, мы получим карту, которую в силу сделанного предположения можно правильно раскрасить двумя красками (смотрите первый рисунок из приведённых ниже).

Восстановим затем отброшенную окружность и по одну сторону от нее, например внутри, изменим цвет каждой области на противоположный (смотрите второй рисунок). Легко видеть, что при этом мы получим карту, правильную раскрашенную двумя красками, но только теперь уже при n+1 окружностях, что и требовалось доказать.

7. Выпуклый многоугольник будем называть «красивым», если выполняются следующие условия:

1) каждая его вершина окрашена в один из трёх цветов;

2) любые две соседние вершины окрашены в разные цвета;

3) в каждый из трёх цветов окрашена, по крайней мере, одна вершина многоугольника.

Доказать, что любой красивый n-угольник можно разрезать не пересекающимися диагоналями на «красивые» треугольники.

Воспользуемся методом математической индукции.

База индукции. При наименьшем из возможных n=3 утверждение задачи очевидно: вершины «красивого» треугольника окрашены в три разных цвета и никакие разрезы не нужны.

Предположение индукции. Допустим, что утверждение задачи верно для любого «красивого» n-угольника.

Индукционный шаг. Рассмотрим произвольный «красивый» (n+1)-угольник и докажем, используя предположение индукции, что его можно разрезать некоторыми диагоналями на «красивые» треугольники. Обозначим через А₁, А₂, А₃, … А_n, А_n+1 – последовательные вершины (n+1)-угольника. Если в какой-либо из трёх цветов окрашена лишь одна вершина (n+1)-угольника, то, соединив эту вершину диагоналями со всеми не соседними с ней вершинами, получим необходимое разбиение (n+1)-угольника на «красивые» треугольники.

Если в каждый из трёх цветов окрашены не менее двух вершин (n+1)-угольника, то обозначим цифрой 1 цвет вершины А₁, а цифрой 2 цвет вершины А₂. Пусть k – такой наименьший номер, что вершина А_k окрашена в третий цвет. Понятно, что k > 2. Отсечём от (n+1)-угольника диагональю А_k–2А_k треугольник А_k–2 А_k–1А_k. В соответствии с выбором числа k все вершины этого треугольника окрашены в три разных цвета, то есть этот треугольник «красивый». Выпуклый n-угольник А₁А₂ … А_k–2А_kА_k+1 … А_n+1, который остался, также, в силу индуктивного предположения, будет «красивым», а значит разбивается на «красивые» треугольники, что и требовалось доказать.

8. Доказать, что в выпуклом n-угольнике нельзя выбрать больше n диагоналей так, чтобы любые две из них имели общую точку.

Проведём доказательство методом математической индукции.

Докажем более общее утверждение: в выпуклом n-угольнике нельзя выбрать больше n сторон и диагоналей так, чтобы любые две из них имели общую точку. При n = 3 утверждение очевидно. Допустим, что это утверждение верно для произвольного n-угольника и, используя это, докажем его справедливость для произвольного (n+1)-угольника.

Допустим, что для (n+1)-угольника это утверждение неверно. Если из каждой вершины (n+1)-угольника выходит не больше двух выбранных сторон или диагоналей, то всего их выбрано не больше чем n+1. Поэтому из некоторой вершины А выходит хотя бы три выбранных стороны или диагонали AB, AC, AD. Пусть АС лежит между АВ и AD. Поскольку любая сторона или диагональ, которая выходит из точки С и отличная от СА, не может одновременно пересекать АВ и AD, то из точки С выходит только одна выбранная диагональ СА.

Отбросив точку С вместе с диагональю СА, получим выпуклый n-угольник, в котором выбрано больше n сторон и диагоналей, любые две из которых имеют общую точку. Таким образом, приходим к противоречию с предположением, что утверждение верно для произвольного выпуклого n-угольника.

Итак, для (n+1)-угольника утверждение верно. В соответствии с принципом математической индукции утверждение верно для любого выпуклого n-угольника.

9. В плоскости проведено n прямых, из которых никакие две не параллельны и никакие три не проходят через одну точку. На сколько частей разбивают плоскость эти прямые.

С помощью элементарных рисунков легко убедится в том, что одна прямая разбивает плоскость на 2 части, две прямые – на 4 части, три прямые – на 7 частей, четыре прямые – на 11 частей.

Обозначим через N(n) число частей, на которые n прямых разбивают плоскость. Можно заметить, что

Естественно предположить, что

или, как легко установить, воспользовавшись формулой суммы n первых членов арифметической прогрессии,

Докажем справедливость этой формулы методом математической индукции.

Для n=1 формула уже проверена.

Сделав предположение индукции, рассмотрим k+1 прямых, удовлетворяющих условию задачи. Выделим из них произвольным образом k прямых. По предположению индукции они разобьют плоскость на 1+ k(k+1)/2 частей. Оставшаяся (k+1)-я прямая разобьётся выделенными k прямыми на k+1 частей и, следовательно, пройдёт по (k+1)-й части, на которые плоскость уже была разбита, и каждую из этих частей разделит на 2 части, то есть добавится ещё k+1 часть. Итак,

что и требовалось доказать.

10. В выражении х₁:х₂: … :х_n для указания порядка действий расставляются скобки и результат записывается в виде дроби:

Прежде всего ясно, что в полученной дроби х₁ будет стоять в числителе. Почти столь же очевидно, что х₂ окажется в знаменателе при любой расстановке скобок (знак деления, стоящий перед х₂, относится либо к самому х₂, либо к какому-либо выражению, содержащему х₂ в числителе).

Докажем это утверждение по индукции.

При n=3 можно получить 2 дроби:

так что утверждение справедливо.

Предположим, что оно справедливо при n=k и докажем его для n=k+1.

Пусть выражение х₁:х₂: … :х_k после некоторой расстановки скобок записывается в виде некоторой дроби Q. Если в это выражение вместо х_k подставить х_k:х_k+1, то х_k окажется там же, где и было в дроби Q, а х_k+1 будет стоять не там, где стояло х_k (если х_k было в знаменателе, то х_k+1 окажется в числителе и наоборот).

Теперь докажем, что можно добавить х_k+1 туда же, где стоит х_k. В дроби Q после расстановки скобок обязательно будет выражение вида q:х_k, где q – буква х_k–1 или некоторое выражение в скобках. Заменив q:х_k выражением (q:х_k):х_k+1=q:(х_k·х_k+1), мы получим, очевидно, ту же самую дробь Q, где вместо х_k стоит х_k·х_k+1.

Задачи без решений

1. Доказать, что при любом натуральном n:

а) число 5 n –3 n +2n делится на 4;

б) число n 3 +11n делится на 6;

в) число 7 n +3n–1 делится на 9;

г) число 6 2n +19 n –2 n+1 делится на 17;

д) число 7 n+1 +8 2n–1 делится на 19;

е) число 2 2n–1 –9n 2 +21n–14 делится на 27.

2. Докажите, что (n+1)·(n+2)· … ·(n+n) = 2 n ·1·3·5·…·(2n–1).

3. Доказать неравенство |sin nx| n|sin x| для любого натурального n.

4. Найдите натуральные числа a, b, c, которые не делятся на 10 и такие, что при любом натуральном n числа a n + b n и c n имеют одинаковые две последние цифры.

5. Доказать, что если n точек не лежат на одной прямой, то среди прямых, которые их соединяют, не менее чем n различных.

Источник

Метод математической индукции.

В этой статье сначала остановимся на основных понятиях, далее рассмотрим сам метод математической индукции и разберем примеры его применения при доказательстве равенств и неравенств.

Навигация по странице.

Индукция и дедукция.

Индукцией называют переход от частных утверждений к общим. Напротив, переход от общих утверждений к частным называется дедукцией.

Пример частного утверждения: 254 делится на 2 без остатка.

Из этого частного утверждения можно сформулировать массу более общих утверждений, причем как истинных так и ложных. К примеру, более общее утверждение, что все целые числа, оканчивающиеся четверкой, делятся на 2 без остатка, является истинным, а утверждение, что все трехзначные числа делятся на 2 без остатка, является ложным.

Таким образом, индукция позволяет получить множество общих утверждений на основе известных или очевидных фактов. А метод математической индукции призван определить справедливость полученных утверждений.

В качестве примера, рассмотрим числовую последовательность: , n – произвольное натуральное число. Тогда последовательность сумм первых n элементов этой последовательности будет следующая

Исходя из этого факта, по индукции можно утверждать, что .

Доказательство этой формулы приведем чуть ниже.

Метод математической индукции.

В основе метода математической индукции лежит принцип математической индукции.

То есть, доказательство по методу математической индукции проводится в три этапа:

Примеры доказательств уравнений и неравенств методом математической индукции.

Вернемся к предыдущему примеру и докажем формулу .

Метод математической индукции предполагает доказательство в три пункта.

Докажем, что отталкиваясь от справедливого равенства из второго пункта.

Сумма k+1 первых членов последовательности представляется как сумма первых k членов исходной числовой последовательности и k+1 ого члена:

Так как из второго пункта, то

Осталось привести дроби к общему знаменателю, привести подобные слагаемые, воспользоваться формулой сокращенного умножения квадрат суммы и произвести сокращение:

Следовательно, доказано равенство третьего пункта.

Таким образом, выполнены все три шага метода математической индукции и тем самым доказано наше предположение о формуле .

Давайте рассмотрим тригонометрическую задачу.

Докажите тождество .

Так как по формуле из тригонометрии

то

Доказательство равенства из третьего пункта завершено, следовательно, исходное тождество доказано методом математической индукции.

Формула бинома Ньютона может быть доказана методом математической индукции.

Пример доказательства неравенства методом математической индукции можете посмотреть в разделе метод наименьших квадратов при выводе формул для нахождения коэффициентов аппроксимации.

Источник

Индукция и комбинаторика

Метод математической индукции

Таким образом доказательство «по индукции» состоит из двух этапов.

Пример 1. Доказать, что при n>= 1

Докажем тогда, что при n=k+1

Пример 2. Доказать, что для любого 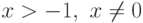-1,\ x \ne 0″ style=»display: inline; «>, и натурального n>= 2 выполнено неравенство (1+x) n > 1 +nx (это неравенство называют неравенством Бернулли).

Такая формулировка будет использоваться, в частности, при доказательствах индукцией по построению объекта.

Для доказательства некоторого свойства объектов индуктивно определенного класса метод математической индукции применяется в следующем виде.

Рассмотрим эту схему на примере простых арифметических выражений.

также являются арифметическими формулами из 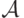и каждая из этих формул имеет глубину .

Докажем, что в каждой арифметической формуле из скобки расставлены правильно.

Источник