Что такое метод координат расскажите о нем

Координаты на прямой

Исследование свойств геометрических тел привело к возникновению отдельной науки — аналитической геометрии. Основополагающим открытием, позволяющим решать задачи, связанные с фигурами, стал координатный метод. В математике принято под координатами понимать положение точки на линии, поверхности или пространстве.

Особенностью способа является нахождение геометрических тел уравнениями. Такой подход позволяет исследовать фигуры и решать задания, взяв за основу алгебраические формулы.

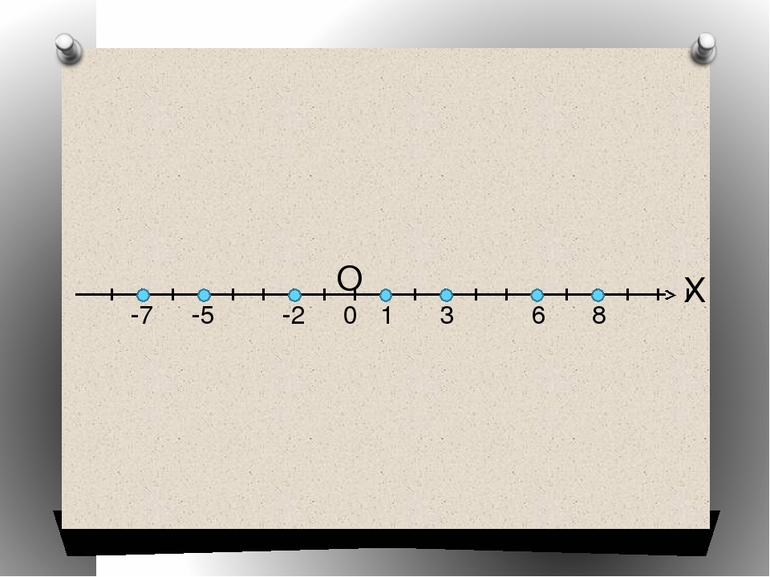
Самая элементарная задача, дающая возможность разобраться в сути, связана с определением положения точки на прямой. Пусть на линии указаны две произвольные точки A и B. Отрезок, который они ограничивают, принимают за единицу длины. Каждой точке P, входящей в AB, соответствует величина, называемая координатой.

Принимать она может три значения:

При выполнении этих условий отрезок называют числовой осью, а A — началом координат. Любая точка, располагающаяся на прямой, имеет свою координату, отличную от других. Но при этом каждое действительное число указывает на расположение точки на рассматриваемой числовой оси. Например, запись вида A (2), B (-¾) обозначает, что числа в скобках являются координатами соответствующих точек.

Расположение на плоскости

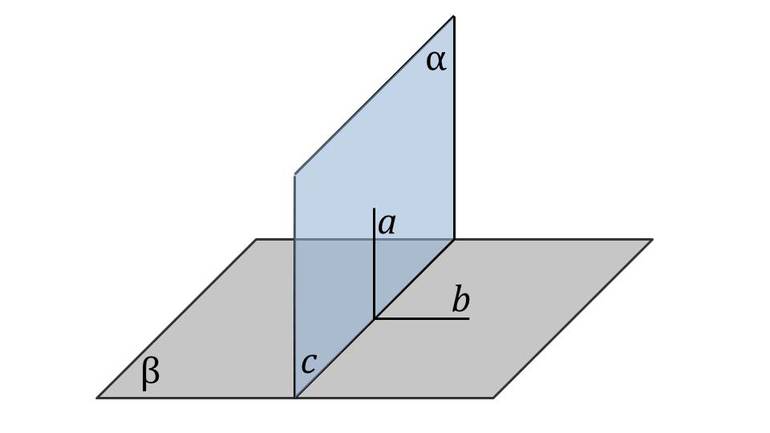
Пусть существуют две плоскости, образующие между собой прямой угол. Их точка пересечения A является началом отсчёта любой из них. Если ось одной плоскости обозначить за X, а второй — за Y, то общим для них пространством будет Axy. Ось, совпадающая с X, называется абсциссой, а Y — ординатой. Единица длины для них одинакова. Пересекающиеся оси образуют четверти. Нумерацию принято вести с верхней правой части против часовой стрелки.

Пусть в плоскости Axy находится произвольная точка. Проведя с неё перпендикуляры на оси, получим два пересечения. Числовые значения в этих местах и будут определять положение A на плоскости, то есть её координаты. Записывают их как A (x, y) и называют декартовыми. Таким образом, нахождение A сводится к определению двух точек, лежащих на осях x и y.

Когда точка располагается на оси X, то её ордината имеет нулевое значение, а если Y — абсцисса. В зависимости от того, в какой четверти находится исследуемый объект, определяется знак его координат. В первой оба числа положительные, а в третьей — отрицательные. Во второй же абсцисса имеет положительное значение, а ордината — отрицательное. В третьей же знаки координат обратные второй четверти.

Естественно, что каждой точке на плоскости соответствует пара чисел. Любая фигура состоит из множества точек. Проведя учёт точек и зная их взаимоотношение относительно друг друга, можно изучить свойство объекта. Эти вычисления позволяет выполнить алгебра и арифметика. Поэтому появляется возможность решать геометрические задачи наглядными алгебраическими способами.

В этом и лежит основа использования метода координат в пространстве. Формулы, применяемые при расчётах, хотя и выглядят устрашающе, на самом деле запоминаются легко. Правда, для этого следует выполнить несколько практических заданий.

Скалярное произведение

Пусть есть два вектора a и b с известными координатами (x1, y1) и (x2, y2). Формула для выражения скалярного произведения векторов через координаты будет иметь вид: a* b = x1*x2 + y1*y2. То есть это сумма произведений соответствующих координат.

Для доказательства следует отложить два вектора из одной точки, направленные в разные стороны. Соединив их конечные точки, можно утверждать, что полученный вектор будет равняться разности a и b. Для образованного треугольника выполняется теорема косинусов: AB 2 = OA 2 + OB 2 — 2*OA*OB * cosα. Так как AB — это всё равно, что длина вектора по модулю в квадрате, то вместо AB можно написать вектор, равный a-b.

В итоге получится: |a-b| 2 = |a| 2 + |b| 2 — 2 |a|*|b|*cosα. Последнее перемножение на косинус по определению является скалярным произведением a и b. Выразив его из выражения, справедливо будет записать: a*b = (|a| 2 + |b| 2 — |a — b| 2 ) /2. Подставив координаты в формулу, получим следующее: a*b = (x1 2 + y1 2 + x2 2 + y2 2 — (x1-x2) 2 + (y1-y2) 2 ) /2 = x1*x2 + y1*y2. Равенство доказано.

Основные формулы

Кроме нахождения длины отрезка, к основным формулам относят:

Для понимания формул нужно знать о векторном и смешанном произведении векторов, а также об определителе матрицы. Зная их, можно решать задачи по вычислению элементов простейших многогранников, находить площади и объёмы.

Нахождение угла

Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:

Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.

Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:

Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2 ½ * ¾ ½ ) = 1 / (6 ½ /2) = 2/6 ½ = 6 ½ / 3. Соответственно, угол равен: α = arccos = 6 ½ / 3.

Вычисление площади и высоты

Таким образом, у треугольника две стороны равны, а значит, он равнобедренный. У найденных сторон общей точкой является B (вершина). Следовательно, углы A и C будут равны. Что и требовалось доказать.

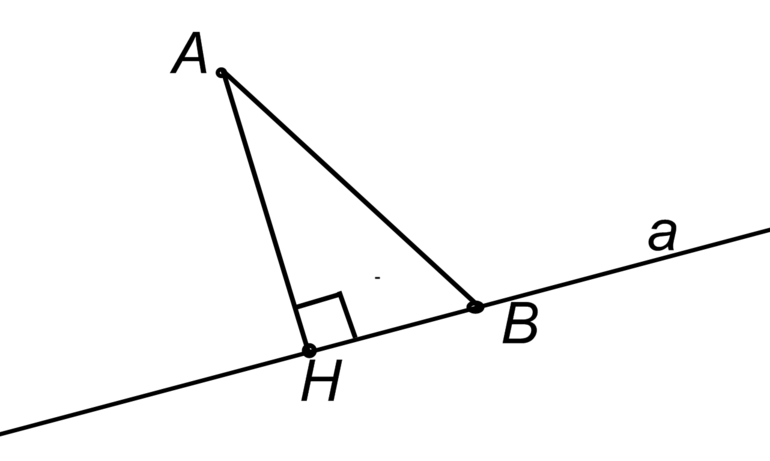
Для того чтобы найти площадь треугольника, используется правило, что она находится умножением высоты на длину стороны, к которой проведена, и делением полученного результата на два: S = h*a/2 = BH * AC /2, где H — точка пересечения высоты и основания.

В равнобедренном треугольнике высота является биссектрисой и медианой, поэтому H лежит на середине отрезка AC. Чтобы найти её положение, используют формулу нахождения координат середины отрезка: H (x, y): X = (-2+4) /2 = 1, Y = (-3+5) / 2 = 1. Искомая точка имеет координаты H (1,1).

Высота находится как корень квадратный из двух точек: BH = ((-3−1) 2 + (4−1) 2 ) ½ = (16+9) ½ = 5. Теперь нужно найти основание треугольника AC. Разницы, из какой координаты вычитать другую, нет, так как результат учитывается по модулю. Основание будет равно: AC = ((-2−4) 2 + (-3−5) 2 ) ½ = (36 + 64) ½ = 10. Полученные значения высоты и основания подставляют в формулу нахождения площади и получают, что она равна: S = 5*10/2 = 25. Задача решена.

Расчёт на онлайн-калькуляторе

Существуют сервисы, позволяющие решать геометрические задачи координатным методом без утомительных самостоятельных вычислений. Сам расчёт обычно занимает не более трёх секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться услугами таких сайтов сможет любой пользователь интернета, даже не имеющий представления о геометрии. Всё, что от него требуется — это подключение к сети и веб-обозреватель с поддержкой Flash-технологии.

Пользователю необходимо ввести условие задания, при этом система будет сама направлять действия и в случае каких-либо ошибок укажет на них, а затем нажать кнопку «Рассчитать». Привлекательность таких сайтов состоит ещё и в том, что ответ будет содержать объяснения с необходимыми формулами и рисунками.

Источник

Метод координат

Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв). Числа (символы), определяющие положение точки (тела) на прямой, плоскости, в пространстве, на поверхности и так далее, называются её координатами. В зависимости от целей и характера исследования выбирают различные системы координат.

См. также

Литература

Полезное

Смотреть что такое «Метод координат» в других словарях:

Метод Хука — Дживса (англ. Hooke Jeeves), также как и алгоритм Нелдера Мида, служит для поиска безусловного локального экстремума функции и относится к прямым методам, то есть опирается непосредственно на значения функции. Алгоритм делится на две… … Википедия

Метод главных компонент — (англ. Principal component analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях,… … Википедия

Метод Главных Компонент — (англ. Principal components analysis, PCA) один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях, таких как… … Википедия

метод — метод: Метод косвенного измерения влажности веществ, основанный на зависимости диэлектрической проницаемости этих веществ от их влажности. Источник: РМГ 75 2004: Государственная система обеспечения еди … Словарь-справочник терминов нормативно-технической документации

МЕТОД ИЗОХРОН — математический метод обработки экспериментальных данных, применяемый для установления истинного возраста гр. одновозрастных м лов или г. п. На основании аналитических данных, по содержанию радиоактивных элементов и продуктов их распада полученных … Геологическая энциклопедия

Метод оскулирующих элементов — (Небесная механика) метод качественного анализа траектории возмущённого движения небесного тела. Для улучшения этой статьи желательно?: Дополнить статью (статья слишком короткая либо содержит лишь словарное определение). Найти и… … Википедия

Метод Тёрнера — Метод Тернера классический метод астрофотометрии, предназначен для калибровки координат камеры. Предложен Гербертом Тёрнером в 1893 году.[1] В основу метода положено разложение в ряд функции отображения из небесных координат в… … Википедия

Метод координирования — Метод измерения крена здания (сооружения), при котором вокруг объекта прокладывают замкнутый полигонометрический ход и вычисляют координаты трех или четырех постоянно закрепленных точек, с которых через определенные промежутки времени засечкой… … Словарь-справочник терминов нормативно-технической документации

МЕТОД ВРАЩЕНИЯ КРИСТАЛЛА — способ получения дифракционной картины, возникающей в монокристалле, вращаемом около заданного направления при облучении монохроматическими рентгеновыми лучами. Пленка, на которой фиксируется дифракционная картина, называется рентгенограммой… … Геологическая энциклопедия

Метод Гаусса — Жордана — используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь… … Википедия

Источник

Класс: 9

Презентация к уроку

Профиль класса: физико-математический

Тип урока – повторительно-обобщающий, 45 мин.

Ход урока

1.1. Взаимное приветствие учителя и учащихся

1.2. Сообщение темы и цели урока.

1.3. Настрой на урок.

Цель: Выяснить у ответственных учеников о готовности учащихся к уроку.

II. Проверка домашнего задания: №902; №1000а; №1044а; 1041а.

3 мин.№900. Дано: ABC, A(4;8), B(12;11), C(7;0)

Доказать: ABC – равнобедренный, но не равносторонний.

1) d=

AB=

2) AC=

3) BC=

Так как AB=AC, то ABC – равнобедренный с основанием BC.

Ответ: ABC– равнобедренный с основанием BC.

№1000.

Выяснить: Является ли это уравнение уравнением окружности, если “да”, то найти координаты центра и радиус окружности.

Ответ: R=5; (1;-2) – координаты центра данной окружности.

№1041.

Дано: , ,

Найти:

=

=

Ответ:

№1044(а).

Дано:

Найти:

x₁x₂+y₁y₂

а) “Из истории возникновения и развития метода координат”. Приготовил: Патрашкин Егор.

Первоначально идея координат зародилась в древности в связи с потребностями астрономии, географии, живописи. Так, на стене одной из древнеегипетских погребальных камер была обнаружена квадратная сетка (палетка), которой пользовались для увеличения изображений

Древнегреческий астроном Клавдий Птолимей применил географические координаты для определения местонахождения мореплавателя. Идеей координат пользовались в середине века для определения положения светил на небе, для определения места на поверхности Земли. Прямоугольной сеткой пользовались художники эпохи Возрождения.

Применять координаты в математике впервые стали Ферма и Декарт. В 1637 году вышла книга Декарта Рассуждения о методе, в которой наряду с общими философскими рассуждениями о материи значительное место уделяется универсальной математике.

Заслуга Декарта состояла в том, что он ввел переменные координаты.

Так, в уравнении ах + ву = с,

буквы х и у стали рассматриваться не как неизвестные, а как переменные.

Метод координат позволяет строить графики уравнений, изображать геометрически различные зависимости, выраженные аналитически с помощью уравнений и формул, решать различные геометрические задачи с помощью алгебры. Термины абсцисса, ордината были введены в употребление Г. Лейбницем в 70, 80-е годы XVII в.

Выполнил Путрин Антон:

Дан треугольник ABC, где M – середина отрезка AB. Найти координаты M, если A(3;5), а B(3;8).

Источник

Метод координат

«Лучше один раз увидеть, чем сто раз услышать», — гласит народная мудрость. Действительно, рисунки, схемы, чертежи и графики способны заменить нам долгие разъяснения.

Мы с вами рассмотрим прямоугольную систему координат. Её также называют прямоугольной декартовой системой координат — в честь французского математика Рене Декарта.

Нарисуем на листе в клетку две перпендикулярные оси, точку их пересечения обозначим через О.

Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 («ноль»). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе по оси ОУ. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси ОУ).

Посмотрите на шахматную доску. Вдоль её нижнего края идет ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.

Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями. Далее мы будем работать только в первой координатной четверти.

Пример. Известны координаты пятнадцати точек:

А(4, 1), В(4, 2), С(1, 2), Д(4, 5), Е(2, 5), F(4, 7), G(3, 7), H(5, 9), I(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1).

Мы провели работу по декодированию графического изображения, состоящего из 15 соединённых отрезками точек, заданных с помощью декартовых прямоугольных координат. Другими словами, мы изменили форму представления информации с числовой на графическую.

Об использовании метода координат в игре Морской бой можно прочитать в § 3.7.

Самое главное

6. Игра «Шифровальщик». Выполните действия по следующему плану:

1) на листочке в клетку нарисуйте произвольный многоугольник;
2) пронумеруйте его вершины и закодируйте их с помощью координат:
3) задайте порядок соединения вершин;
1) проверьте, не допущена ли вами ошибка при кодировании рисунка;
5) координаты точек и порядок их соединения выпишите на отдельный листок;
6) предложите кому-нибудь восстановить ваш рисунок по этому коду;
7) сравните результаты — возможно искажение информации при декодировании.

Босова Л. Л., Информатика и ИКТ : учебник для 5 класса Л. Л. Босова. М. : БИНОМ. Лаборатория знаний, 2009. 192 с. : ил.

Источник

Курсовая работа: «Метод координат и его применение»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Метод координат и его применение

Введение

Метод координат имеет применение во многих областях современной человеческой деятельности, он лежит в основе таких наук, как механика, геодезия, астрономия.

Идея геометрии Декарта состоит в том, что геометрический объект задается уравнением, связывающим переменные величины. По свойствам уравнения судят о свойствах геометрического объекта.

Декарт считается одним из основателей новой математики. Его имя сохранили термины: «декартовы координаты», «декартов лист», «правило знаков Декарта», «метод неопределенных коэффициентов Декарта».

Основные понятия в аналитической геометрии взяты из обычной, но записываются языком алгебры, становящейся вследствие этого средством исследования геометрических форм.

Характерной особенностью метода координат является определение геометрических фигур уравнениями, что позволяет производить геометрические исследования и решать геометрические задачи средствами алгебры.

Придавая геометрическим исследованиям алгебраический характер, метод координат переносит в геометрию наиболее важную особенность алгебры — единообразие способов решения задач. Если в арифметике и элементарной геометрии приходится, как правило, искать для каждой задачи особый путь решения, то в алгебре и аналитической геометрии решения проводятся по общему для всех задач плану, легко приспособляемому к любой задаче. Можно сказать, что аналитическая геометрия занимает такое же положение по отношению к элементарной геометрии, какое алгебра занимает относительно арифметики. Перенесение в геометрию свойственных алгебре и поэтому обладающих большой общностью способов решения задач составляет главную ценность метода координат. Следует, однако, предостеречь читателя от пренебрежительного отношения к приёмам элементарной геометрии, так как в отдельных случаях они позволяют находить изящные решения, более простые, чем получаемые методом координат.

Другое достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.

Таким образом, метод координат имеет важное практическое значение и следовательно цель данной работы заключается в следующем: изучить основы «метода координат» и его применение.

Задачи данной работы:

— Исследовать использование «метода координат» при решении геометрических задач;

— установить какой из методов решения лучше;

Сущность метода координат

Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно истолковывать алгебраические и аналитические соотношения и факты геометрически и таким образом применять геометрию к решению алгебраических задач.

Метод координат – это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.

В некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрическими способами. Метод координат связан, правда, с одной геометрической сложностью. Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат. И только достаточный опыт позволяет выбирать систему координат наиболее целесообразно.

Метод координат на плоскости

2.1. Аффинная система координат на плоскости.

Определение. Аффинная система координат (или аффинным репером) на плоскости называется упорядоченная тройка точек этой плоскости не лежащих на одной прямой: R =<О, Е₁, Е₂>.

Обратно если дана упорядоченная тройка R =<О, е₁, е₂>, состоящая из точки О и двух неколлинеарных векторов е₁ и е₂, то от неё легко перейти к тройке R =<О, Е₁, Е₂>, отложив векторы е₁ и е₂ от точки О и взяв соответственно концы этих векторов Е₁ и Е₂: е₁= ОЕ₁ и е₂ = ОЕ₂. Ясно, что точки О, Е₁, Е₂, не будут лежать на одной прямой, так как векторы е₁ и е₂ не коллинеарны.

Таким образом, мы приходим к выводу, что задание на плоскости системы координат как упорядоченной тройки точек R =<О, Е₁, Е₂>, не лежащих на одной прямой, равносильно заданию её как упорядоченной тройки R =<О, е₁, е₂>, состоящей из точки О и двух неколлинеарных векторов е₁ и е₂. В результате в геометрическую картину, составленную из точек, вводятся векторы.

Первая точка О в системе координат R называется началом системы координат, а векторы е₁ и е₂ – её базисными или координатными векторами. Прямая ОЕ₁ с направляющим вектором е₁ называется координатной осью Ох, или осью абсцисс, а прямая ОЕ₂ с направляющим вектором е₂ называется координатной осью Оу, или осью ординат.

Пусть на плоскости задана система координат R =<О, е₁, е₂> и произвольная точка М. Вектор ОМ = r _м называется радиус-вектором точки М относительно точки О (или системы координат R ).

Определение. Координатами точки М в системе координат R =<О, е₁, е₂> называются координаты её радиус-вектора ОМ в базисе е₁, е₂, то есть коэффициенты х, у в его разложении в линейную комбинацию векторов базиса: М(х, у) _R  ОМ = хе₁+ уе₂.

Итак, понятие координат точки тесно связывается с понятием координат вектора, а понятие системы координат для точек – с понятием базиса векторов. «Привязывая» векторный базис к фиксированной точке плоскости (началу координат), мы приходим к системе координат для точек. Если тот же векторный базис «привязать» к другому началу, мы получим другую систему координат для точек.

Векторы а и в коллинеарны тогда и только тогда, когда их координаты пропорциональны.

Каждой точке М плоскости поставим в соответствие вектор ОМ. Координаты вектора ОМ называются координатами точки М в данной аффинной системе координат. При этом если ОМ = (х, у), то пишут: М (х, у).

Пусть прямые, проведенные через точку М параллельно осям координат, пересекают оси координат соответственно в точках М₁ и М₂ (рис. 2).

Пусть точка С делит отрезок АВ в данном отношении:

Тогда . Из правил действии над векторами в координатах следует, что координаты точки С определяются формулами:

,

В частности, если С – середина отрезка АВ, то

,

Рассмотрим различные способы задания прямой на плоскости.

где t – некоторое число (параметр). Это соотношение в координатах запишется так:

Полученные уравнения называют параметрическими уравнениями прямой.

При и эти уравнения равносильны следующему уравнению первой степени:

,

которое называется уравнением прямой, проходящей через две точки.

В частности, если прямая l проходит через точки А (а, 0) и В (0, b ), отличные от начала координат, то уравнение прямой принимает вид

Это уравнение называется уравнением прямой в отрезках.

где . Число k называют угловым коэффициентом прямой. В частном случае, при х₁ = 0 и у₁ = b , уравнение принимает вид

Таким образом, всякую прямую на плоскости можно задать уравнение первой степени Ах + Ву + С = 0, где хотя бы одно из чисел А и В отлично от нуля. Верно и обратное предложение: всякое уравнение первой степени Ах + Ву + С = 0 есть уравнение некоторой прямой в аффинной системе координат на плоскости.

,

Если же В = 0 и , то оно принимает вид х = а, где .

2.2. Декартова система координат на плоскости. Прямая и окружность.

При решении задач, в которых существенную роль играет понятие расстояния между двумя точками, применяется, декартова или прямоугольная система координат.

.

Пользуясь формулой, запишем уравнение окружности с центром в точке С ( a , b ) и радиусом r :

.

.

Если l ₁ || l ₂, то , поэтому k ₁ = k ₂, и обратно, т.е. условие k ₁ = k ₂ выражает признак параллельности прямых l ₁ и l ₂.

Введем формулу для вычисления угла между пересекающимися прямыми l ₁ и l ₂ (рис. 5).

Так как и , , то

Полученную формулу для вычисления угла от прямой l ₁ до прямой l ₂ можно записать и так:

Приступая к решению геометрической задачи, следует рационально выбрать систему координат, присоединить её к данной фигуре наиболее естественным образом. Желательно, чтобы данные точки располагались на осях координат, тогда среди координат будут нули. Это позволит упростить вычисления.

2.3. Полярная система координат на плоскости

Уравнения многих кривых удобно задавать не в декартовой системе, а в других системах координат. Координатами называются числа, при помощи которых можно определить положение точки. Например, положение точки на поверхности земного шара определяются ее географическими координатами – шириной и долготой. Одной из важных систем координат на плоскости является полярная система координат.

Полярная система координат задается точкой О и лучом ОА с началом в этой точке. Точка О называется полюсом, ось ОА – полярной осью. Полярными координатами точки М называются ее расстояние r от полюса и угол , который направленный отрезок ОМ образует с полярной осью.

3.Метод координат в пространстве

3.1. Декартова прямоугольная система координат в пространстве

Координаты точек и векторов.

Декартова прямоугольная система координат в пространстве задается тремя попарно перпендикулярными осями координат с общим началом:

Ох – ось абсцисс, Оу – ось ординат, Оz – ось аппликат.

Радиус-вектором точки М относительно декартовой прямоугольной системы координат Охуz называется вектор . Координатами точки М относительно декартовой прямоугольной системы координат называются проекции ее радиус-вектора на оси координат:

х=Пр_х , у=Пр_у , z=Пр_{z ,} т.е. скалярные величины направленных отрезков на осях Ох, Оу, Оz:

где P, Q, R – проекции точки М на оси Ох, Оу, Оz соответственно. При этом пишут

Существует определения координат вектора.

Определение. Координатами вектора относительно декартовой прямоугольной системы координат Охуz называются его проекции на оси координат: а_х=Пр_х, а_у=Пр_у, а_z=Пр_z. При этом употребляется запись =( а_х ,а_у, а_z).

Координаты вектора равны разностям между координатами его конца и начала: если , то

, , выражение координат вектора через координаты его начала и конца. Действительно, . Следовательно,

.

Аналогичным образом можно найти выражения для , .

3.2. Цилиндрическая система координат в пространстве 3

Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем (r,θ,h). В терминах декартовой системы координат,

( радиус ) — расстояние от оси z к точке P,

( азимут или долгота) — угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость

h (высота) — расстояние (с учетом знака) от xy-плоскости до точки P.

Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение 2x + 2y = 2c, тогда как в цилиндрических оно выглядит как r = с

Пример: Найти центр тяжести однородного тела, ограниченного сферой и параболой .

Воспользуемся формулами , , ,

( V ₁): , , , а интеграл в виде

Следовательно, . Таким образом, центр тяжести данного тела находится в точке .

Замечание. Неравенства, определяющие область V ₁ получены следующим образом. Уравнение определяется пересечением параболоида и сферы . Откуда, , z =1 и в цилиндрической системе координат . Следовательно, ; функции , ; а .

3.3. Сферическая система координат

Сферическая система координат определяется так 4 :

При  =90  сферическая система координат вырождается в полярную.

.

Стереографической проекцией называется проекция сферы из одного полюса (скажем южного) на касательную плоскость к другому полюсу (северному). Стереографическая проекция является взаимно однозначным отображением сферы с выколотой точкой на плоскость. С ее помощью можно получать плоское изображение сферы (например, земной поверхности или « небесной сферы»), и поэтому ею с давних времен пользуются астрономы и картографы.

Изобретение стереографической проекции обычно приписывают греческому астроному Гиппарху, жившему 160-125 гг. до н. э.; впоследствии, ее использовали навигаторы, кристаллографы, геологи и всесторонне изучали математики. Стереографическая проекция лежит в основе работы астролябии.

Пример. Найти объем, ограниченный поверхностями , , , где α

Область изменения переменных характеризуется неравенствами: , .

Решение: Введем сферические координаты по формулам: , , .

Область новых переменных характеризуется следующими неравенствами: , .

Так как z >0, то и cos θ >0, поэтому окончательно имеем неравенства: , .

Таким образом, при любых данных r и θ переменное φ может иметь любые значения от 0 до 2π, переменное r может при данном θ изменяться от 0 до 2 a cos φ, а угол θ может изменятся от α до β. Итак, объем вычисляем по формуле:

4. Уравнения геометрических мест точек

4.1. Определение геометрического места точек

Геометрическое место точек – это множество всех точек, удовлетворяющих определённым заданным условиям.

Пример 1. Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO AB и AO = OB:

Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d. Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.

4.2. Определение уравнения геометрического места точек

Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линии и только они.

Чтобы составить уравнение линии как геометрического места точек, обладающих одинаковым свойством, нужно:

1) взять произвольную (текущую) точку M(x, y) линии;
2) записать равенством общее свойство всех точек M линии;
3) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки M(x, y) и через данные в задаче.

В прямоугольных координатах уравнение прямой на плоскости задается в одном из следующих видов:

1. Уравнение прямой с угловым коэффициентом

Уравнением (1) может быть определена любая прямая на плоскости, не перпендикулярная оси Ox.

Уравнение прямой с угловым коэффициентом разрешено относительно текущей координаты y.

2. Общее уравнение прямой

Частные случаи общего уравнения прямой:

а) Если C = 0, уравнение (2) будет иметь вид

и прямая, определяемая этим уравнением, проходит через начало координат, так как координаты начала координат x = 0, y = 0 удовлетворяют этому уравнению.

б) Если в общем уравнении прямой (2) B = 0, то уравнение примет вид

Ax + С = 0, или .

Уравнение не содержит переменной y, а определяемая этим уравнением прямая параллельна оси Oy.

в) Если в общем уравнении прямой (2) A = 0, то это уравнение примет вид

By + С = 0, или ;

уравнение не содержит переменной x, а определяемая им прямая параллельна оси Ox.

Следует запомнить: если прямая параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.

г) При C = 0 и A = 0 уравнение (2) принимает вид By = 0, или y = 0.

Это уравнение оси Ox.

д) При C = 0 и B = 0 уравнение (2) запишется в виде Ax = 0 или x = 0.

Это уравнение оси Oy.

3. Уравнение прямой в отрезках на осях

(3)

Каждый из этих отрезков отложен от начала координат.

Особенности этого уравнения такие: в левой части уравнения между дробями сосит знак плюс, величины a и b могут быть как положительными, так и отрицательными, правая часть уравнения равна единице.

4. Нормальное уравнение прямой

(4)

(5)

причем перед дробью следует выбрать знак, противоположный знаку свободного члена C в общем уравнении прямой (2).

Особенности нормального уравнения прямой: сумма квадратов коэффициентов при текущих координатах равна единице, свободный член отрицателен, а правая его часть равна нулю.

5. Построение прямой по ее уравнению

Прямая вполне определена, если известны две принадлежащие ей точки. Для того чтобы построить прямую по ее уравнению, надо, пользуясь этим уравнением, найти координаты двух ее точек. Твердо следует помнить, что если точка принадлежит прямой, то координаты этой точки удовлетворяют уравнению прямой.

Если прямая определена общим уравнением Ax + By + C = 0 и , то для ее построения проще всего определить точки пересечения прямой с координатными осями.

Укажем, как определить координаты точек пересечения прямой с координатными осями. Координаты точки пересечения прямой с осью Ox находят из следующих соображений: ординаты всех точек, расположенных на оси Ox, равны нулю. В уравнении прямой полагают, что y равно нулю, и из полученного уравнения находят x. Найденное значение x и есть абсцисса точки пересечения прямой с осью Ox. Если окажется, что x = a, то координаты точки пересечения прямой с осью Ox будут (a, 0).

Чтобы определить координаты точки пересечения прямой с осью Oy, рассуждают так: абсциссы всех точек, расположенных на оси Oy, равны нулю. Взяв в уравнении прямой x равным нулю, из полученного уравнения определяют y. Найденное значение y и будет ординатой пересечения прямой с осью Oy. Если окажется, например, что y = b, то точка пересечения прямой с осью Oy имеет координаты (0, b).

Если же в общем уравнении прямой C = 0, то прямая, определяемая этим уравнением, проходит через начало координат. Таким образом, уже известна одна ее точка, и для построения прямой остается только найти еще одну ее точку. Абсциссу x этой точки задают произвольно, а ординату y находят из уравнения прямой.

Если прямая задана уравнением y = kx + b с угловым коэффициентом, то из этого уравнения уже известна величина отрезка b, отсекаемого прямой на оси ординат, и для построения прямой остается определить координаты еще только одной точки, принадлежащей этой прямой. Если в уравнении y = kx + b , то легче всего определить координаты точки пересечения прямой с осью Ox. Выше было указано, как это сделать.

Если же в уравнении y = kx + b b = 0, то прямая проходит через начало координат, и тем самым уже известна одна принадлежащая ей точка. Чтобы найти еще одну точку, следует дать x любое значение и определить из уравнения прямой значение y, соответствующее этому значению x.

5. Применение и значение метода координат

Мысль о возможности систематического применения метода координат в научных исследованиях зародилась несколько тысяч лет тому назад. Известно, например, что астрономы древнего мира, используя специальные системы координат на воображаемой небесной сфере, определяли положение наиболее ярких звёзд, составляли карты звёздного неба, вели отличавшиеся большой точностью наблюдения за перемещением Солнца, Луны и планет относительно неподвижных звёзд. В более позднюю эпоху широко развилось использование системы географических координат для составления карт земной поверхности и определения местонахождения корабля в открытом море. Однако до XVII века применение метода координат имело односторонний характер: им пользовались, по сути, только для указания положения определённого объекта — неподвижного (гора, мыс) или движущегося (корабль, планета).

Метод координат представляет собой глубокий и мощный аппарат, позволяющий привлекать для исследования геометрических объектов. Благодаря универсальности подхода к решению различных задач, метод аналитической геометрии стал основным методом геометрических исследований и широко применяется в других областях точного естествознания – механике, физике.

Сферическая система координат широко применяется в астрономии, в частности при расчетах траектории движения спутников и других объектов. Пример ее использования астролябия.

Стереографическая проекция является взаимно однозначным отображением сферы с выколотой точкой на плоскость. С ее помощью можно получать плоское изображение сферы (например, земной поверхности или « небесной сферы»), и поэтому ею с давних времен пользуются астрономы и картографы.

Изобретение стереографической проекции обычно приписывают греческому астроному Гиппарху, жившему 160-125 гг. до н. э.; впоследствии, ее использовали навигаторы, кристаллографы, геологи и всесторонне изучали математики. Стереографическая проекция лежит в основе работы астролябии.

Полярная система координат двумерная и поэтому может применяться только в тех случаях, когда местонахождение точки определяется на плоскости, или для случая однородности свойств системы в третьем измерении, например, при рассмотрении течения в круглой трубе. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Например, в приведённых выше примерах видно, что простых уравнений в полярных координатах достаточно для определения таких кривых как спираль Архимеда, уравнения которых в прямоугольной системе координат гораздо сложнее. Кроме того, многие физических системы — такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра — гораздо проще моделировать в полярных координатах. Причиной создания полярной системы координат было исследование орбитального и движения по кругу.

Системы с радиальной симметрией очень хорошо подходят для описания в радиальных координатах, где полюс системы координат совпадает с центром симметрии. В качестве примера можно привести уравнение тока грунтовых вод в случае радиально симметричных колодцев. Системы с центральными силами также подходят для моделирования в полярных координатах. К таким системам относятся гравитационные поля, подчиняющиеся закону обратно-квадратичной зависимости, так и системы с точечными источниками энергии, такие как радиоантенны.

Фронт мощности звуковой волны промышленного громкоговорителя показан в сферических полярных координатах при шести частотах. Трёхмерное моделирование звука динамиков может использоваться для прогнозирования их эффективности. Необходимо сделать несколько диаграмм в полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность.

В инженерной деятельности при изучении свойств геометрических объектов используют прямоугольную систему координат, отличающуюся от декартовой системы координат, применяемой в математике, направлением осей.

Заключение

Трудно переоценить значение декартовой системе координат в развитии математики и её приложений. Огромное количество задач, требовавших для решения геометрической интуиции, специфических методов получило решение, состоящее в аккуратном проведении алгебраических выкладок. Метод координат лежит в основе расчетов сложных физических процессов, траектории движения космических и наземных объектов и т.д.

Сферическая и полярная системы координат иногда бывают удобней прямоугольной декартовой, особенно в задачах, связанных с окружностями или дугами кривых. Метод координат позволяет быстро и красиво решать сложные геометрические задачи, он имеет ряд преимуществ по сравнению с векторным методом, даёт наглядное представление на координатной плоскости и в пространстве сложных зависимостей, выраженных формулами, уравнениями. Графики функций позволяют описать свойства этих функций. Многие линии, фигуры можно описать в координатах. Векторный и координатный методы тесно связаны друг с другом. Выбор зависит от условия задачи, поставленного вопроса. Нельзя сказать, что какой-то из методов решения лучше или проще для целой серии задач. Выбор системы координат для конкретных задач более конкретен.

При практическом применении понятия координат координаты предмета, рассматриваемого условно как точка, могут быть определены лишь приближённо. Задание координат предмета означает, что точка, определяемая этими координатами, либо является одной из точек этого предмета либо достаточно близка к нему.

В результате исследования можно сделать вывод, что метод координат (и математика в целом) развивается исходя из практических нужд. В том числе метод координат играет огромную роль не только в геометрии, алгебре, математическом анализе, но и в таких направлениях как физика, динамика, география, астрономия, механика и многие др.

Список литературы

Моденов П.С., Аналитическая геометрия, М., 1969.

Атанасян Л.С., Геометрия, часть 1, М., Просвещение, 1967.

Атанасян Л.С., Геометрия, часть 1, Учебное пособие для студентов математических факультетов педагогических институтов, М., Просвещение, 1973.

Выгодский М.Я., Справочник по высшей математике, М., 1972.

Понтрягин Л.С., Метод координат. М., Наука, 1977.

Атанасян Л.С., Базылев В.Т. и др., Геометрия, М., Просвещение, 1986.

Погорелов А.В., Аналитическая геометрия, 4 изд., М., Наука, 2004.

Энциклопедия элементарной математики. Геометрия, том 4

Атанасян Л.С., Сборник задач по геометрии, часть 1, М., 1973.

Базылев В.Т. и др., Сборник задач по геометрии, М., 1980.

Прасолов В.В., Задачи по стереометрии, М., 1989.

Прасолов В.В., Задачи по планиметрии, часть 2, М., 1986.

Интернет ресурс: http://matschool2005.narod.ru/Lessons/Lesson8.htm

Приложение 1. Задачи, решаемые методом координат с решениями.

Задача 1. Даны уравнения одной из сторон ромба х-3у + 10 = 0 и одной из его

Найдем т. пересечения и :

=> A (-4;2)

=> C (4;0). Через точку C направим прямую, параллельную (т.е. найдем ). => По свойству ромба: => ; =>

; ; ; =>

; По формуле прямой, проходящей через две точки, найдем

;

Задача 2. Даны координаты вершин треугольника АВС. Найти длины медианы, высоты, биссектрисы, проведенных из вершины А. Вычислить внутренний угол при вершине В.

= <-4; 3>, ||=5

Источник