Что такое математическая постановка задачи
Математическая постановка задачи



Первым этапом постановки и решения задачи на ЭВМ является четкая формулировка задачи (обычно на профессиональном языке), выделение исходных данных для ее решения и точные указания относительно того, какие результаты и в каком виде должны быть получены.
Математическая постановка (или формализация) задачи- необходимый и очень важный этап, от которого больше всего зависит результат решения задачи на ЭВМ. Его выполнение требует досконального знания предмета, способности к абстрактному мышлению, владения математическим аппаратом, а также некоторого опыта в решении задач на ЭВМ.
После того как задача сформулирована, необходимо выбрать метод решения, который позволил бы свести ее к последовательности простых этапов. Здесь можно применить метод декомпозиции, т.е. разбить сложную задачу на отдельные относительно обособленные с точки зрения практических приложений части, что позволяет осуществить модульный принцип построения всей задачи в целом.
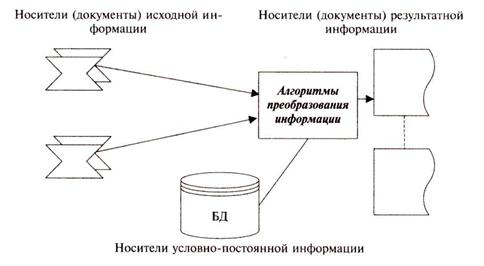
При этом единичный структурно-функциональный элемент рассматривается как отдельная задача (рис.6.1.). Такой подход обеспечивает разработчику возможность распараллелить отдельные работы в ходе написания, отладки и внедрения некоторых программных модулей, входящих в задачу. Главная проблема здесь – учесть все возможные взаимосвязи между задачами и построить на их основе полную и непротиворечивую информационную модель управленческой деятельности организации.
Рис.6.1. Состав задачи для постановки единичного структурно-функционального элемента задачи
В общем виде постановка задачи состоит из четырех принципиально важных компонентов:
1) организационной части ее использования и описания;
2) свода применяемых математических моделей;
3) описания вычислительных алгоритмов;
4) концепции построения информационной модели системы.
Постановка каждой отдельной задачи документально оформляется в виде соответствующего определенного раздела технического задания и занимает значительную часть общего времени.
Математическая модель и разрабатываемые на ее основе алгоритмы должны удовлетворять трем требованиям: определенности (однозначности), инвариантности по отношению к различным альтернативным ситуациям в задаче и результативности (возможности ее решения за конечное число шагов). Результатом алгоритмизации является логически построенная и отлаженная блок-схема.
Наконец, разработка информационной концепции предполагает определение: реквизитов входных и выходных форм, их расположения и взаимосвязи, носителей исходных и результатных данных, состава нормативно-справочной информации, способов информационного взаимодействия разных задач, сроков и периодичности представления и получения данных, а также построение графа взаимосвязи показателей, имеющих отношение к данной задаче. Создается информационная модель конкретной предметной области. Единичный фрагмент этой модели отражает один выходной и несколько входных показателей, исчисляемых на основе расчетных формул.
Постановка задачи начинается на пред проектной, а завершается – на стадии технического проектирования, причем в этой работе главная роль принадлежит специалисту – пользователю системы. Главные обязанности постановщика – заложить основы для проектирования математического и информационного обеспечения, разработки идеологии технического и программного обеспечения, создания концепции организационного и эргономического обеспечения.
Постановка задачи требует от пользователя не только профессиональных знаний предметной области, для которой выполняется постановка, но и владения основами компьютерных информационных технологий. Последствия ошибок пользователя на этапе постановки задачи будут тяжелее в сотни и даже тысячи раз (в зависимости от масштаба системы), если их обнаружат на конечных фазах создания или использования прикладного программного продукта. Объясняется это тем, что каждый из последующих участников создания прикладных программ не располагает информацией, необходимой для исправления содержательных ошибок.
Создание программного продукта может вестись и самим пользователем, причем в отношении простоты построения программы это можно считать более предпочтительным вариантом. Но с позиции профессиональных программистов такие программы могут содержать большое число погрешностей, поскольку они менее эффективны по машинным ресурсам, быстродействию и многим другим традиционным критериям.
Пользователь, как правило, приобретает и применяет готовые программные пакеты, по своим функциям и потребности, ориентированные на определенные виды деятельности, но новую и не имеющую аналогов задачу придется, разрабатывать совместно с разработчиком – программистом. Нередко имеющаяся задача может дополняться разработкой оригинальных прикладных программ, но в любом случае постановка задачи требуется.
Как правило, постановка задачи выполняется в соответствии с определенными требованиями или планом. Приведем пример одного из возможных его вариантов.
План постановки задачи
1. Организационно-экономическая сущность задачи:
— назначение (для каких объектов, подразделений, пользователей предназначена);
— периодичность решения и требования к срокам решения;
— источники и способы получения данных;
— потребители результатной информации и способы ее отправки;
— информационная связь с другими задачами.
2. Описание исходной (входной) информации:
— перечень исходной информации;
— формы представления (документ) по каждой позиции перечня; примеры заполнения документов;
— количество формируемых документов (информации) в единицу времени, количество строк в документе (массиве);
— описание структурных единиц информации (каждого элемента данных, реквизита);
— точное и полное наименование каждого реквизита документа, идентификатор, максимальная разрядность в знаках;
— способы контроля исходных данных;
— контроль разрядности реквизита;
— контроль интервала значений реквизита;
— контроль соответствия списку значений;
— балансовый или расчетный метод контроля количественных значений реквизитов;
— метод контроля с помощью контрольных сумм и любые другие возможные способы контроля.
3. Описание результатной (выходной) информации:
— перечень результатной информации;
— формы представления (печатная сводка, машинный носитель и его макет и т.д.);
— периодичность и сроки представления;
— количество формируемых документов (информации) в единицу времени, количество строк в документе (массиве);
— перечень пользователей результатной информации (подразделение и персонал);
— перечень регламентной и запросной информация; описание структурных единиц информации (каждого элемента данных, реквизита) по аналогии с исходными данными;
— способы контроля результатной информации;
— контроль интервала значений реквизита;
— контроль соответствия списку значений;
— балансовый или расчетный метод контроля отдельных показателей;
— метод контроля с помощью контрольных сумм и любые другие возможные способы контроля.
4. Описание алгоритма решения задачи (последовательности действий и логики решения задачи):
— описание способов формирования результатной информации с указанием последовательности выполнения логических и арифметических действий;
— описание связей между частями, операциями, формулами алгоритма;
— требования к порядку расположения (сортировке) ключевых (главных) признаков в выходных документах, например, по возрастанию значений табельных номеров.
Алгоритм должен учитывать общие и все частные случаи решения задачи. При составлении алгоритма следует использовать условные обозначения (идентификаторы) реквизитов, присвоенные элементам исходной и результатной информации. Допускается описание алгоритма в виде текста. Необходимо предусмотреть контроль вычислений на отдельных этапах, операциях выполнения алгоритма. При этом указываются контрольные соотношения, которые позволяют выявить ошибки.
5. Описание используемой условно-постоянной информации:
— перечень условно-постоянной информации (классификаторов, справочников, таблиц, списков с указанием их полных наименований);
— описание структурных единиц информации (по аналогии с исходными записями);
— способы взаимодействия с переменной информацией.
Наиболее важные вопросы, в решении которых принимает, участие квалифицированный пользователь, связаны с выбором конкретного инструментария, позволяющего построить и реализовать информационные связи в системе. В состав инструментария входят методы накопления и обработки данных, структура и способы размещения массивов на машинных носителях, состав и макеты реквизитов документов и показателей, классификация и группировка показателей, их состав, размещение в базе данных, разновидности применяемых первичных документов и т.п. Вторая группа вопросов касается организации человеко-машинного интерфейса. Традиционно выделяются два способа интенсивного взаимодействия. Первый предполагает реализацию запросно-ответного режима с выполнением пользователем активной функции. Второй отдает инициативу вычислительной системе. Выбор зависит от конкретного сценария диалога и потребностей специалиста, эксплуатирующего систему.
Первоначальные алгоритмы их решения оформляются как задания на программирование уже на этапе технического проектирования. Затем программисты на основании этих разработок строят блок-схемы, кодируют их в виде программ с учетом всех логических переходов и расчетных формул, обеспечивают контроль достоверности данных на входе и выходе, отлаживают каждый программный модуль, подпрограммы и программы в целом, пишут инструкции по эксплуатации и сопровождению проблемных, т.е. ориентированных на решение конкретной практической задачи, программ. В итоге получается готовый для внедрения рабочий проект.
Если в ходе проектирования задачи могут использоваться и стандартные, хорошо отлаженные пакеты прикладных программ, то стадии технического и рабочего проектирования, как правило, совмещаются, а процесс создания задачи сводится в основном к настройке параметров и генерации готовых пакетов. Такая технология проектирования значительно сокращает сроки изготовления программно-технологических продуктов, облегчает и экономит время на освоение их пользователями. Но во всех случаях, необходимо разрабатывать алгоритм решения задачи.
Понятие алгоритма
Алгоритмом называется четкое описание последовательности действий, которые необходимо выполнить для решения задачи. Так как решение практически любой задачи требует получения результата по заданным исходным данным, то можно сказать, что алгоритм описывает последовательный процесс преобразования исходных данных в результат.
Разработать алгоритм решения задачи означает разбить задачу на последовательно выполняемые шаги (этапы), причем результаты выполнения предыдущих этапов могут использоваться при выполнении последующих. При этом должны быть четко указаны как содержание каждого этапа, так и порядок выполнения этапов. Отдельный этап (шаг) алгоритма представляет собой либо другую, более простую задачу, алгоритм решения которой разработан ранее, либо должен быть достаточно простым и понятным без дополнительных пояснений.
Если алгоритм разработан, то его можно поручить выполнить человеку (и вообще любому исполнителю, в том числе и ЭВМ), не знакомому с решаемой задачей, и, точно следуя правилам алгоритма, этот человек (или другой исполнитель) получит ее решение. В этом случае алгоритм может быть представлен на языке программирования.
Алгоритм должен обладать следующими основными свойствами, раскрывающими его определение.
1. Дискретность. Это свойство состоит в том, что алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов (этапов). При этом для выполнения каждого шага (этапа) алгоритма требуется некоторый конечный отрезок времени, т.е. преобразование исходных данных в результат осуществляется во времени дискретно.
2. Определенность (или детерминированность). Это свойство состоит в том, что каждое правило алгоритма должно быть четким и однозначным. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
3. Результативность (или конечность). Это свойство состоит в том, что алгоритм должен приводить к решению задачи за конечное число шагов.
4. Массовость. Это свойство состоит в том, что алгоритм решения задачи разрабатывается в общем виде, т. е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма. (В отдельных случаях исходные данные могут отсутствовать.)
Чтобы разработать алгоритм, нужно хорошо представить себе ход решения задачи. При этом полезно решить задачу самому (на бумаге) для каких-либо наборов данных, не требующих громоздких вычислений, запоминая выполняемые действия так, чтобы далее эти действия формализовать, т. е. записать в виде последовательности четких правил. Понятия алгоритма и программы разграничены не очень четко. Обычно программой называют окончательный вариант алгоритма решения задачи, ориентированный на конкретного исполнителя.
При разработке алгоритма для представления его промежуточных вариантов часто используется язык схем.
Язык схем
Схемой называется наглядное графическое изображение алгоритма, когда отдельные действия (этапы) алгоритма изображаются при помощи различных геометрических фигур (блоков), а связи между этапами (последовательность выполнения этапов) указываются при помощи линий, соединяющих эти фигуры. Термин «блок» употребляется здесь и далее вместо термина «символ», используемого ГОСТом, в связи с употреблением термина «символ» в программировании в другом смысле.
Несмотря на все многообразие решаемых на ЭВМ задач, можно выделить несколько «типичных» действий (этапов), которые в различной последовательности выполняются при решении задач:
1. Присваивание. (Заметим, что присваивание является основной операцией, при помощи которой осуществляется обработка данных.)
2. Проверка условия и выбор в зависимости от результата проверки одного из двух путей вычислительного процесса.
3. Ввод данных и вывод результата.
4. Начало и конец вычислительного процесса.
Конкретные операции указаны внутри фигур в качестве примеров, Рассмотрим выполнение этих действий, а также функции других элементов схем, приведенных на рис.6.1.
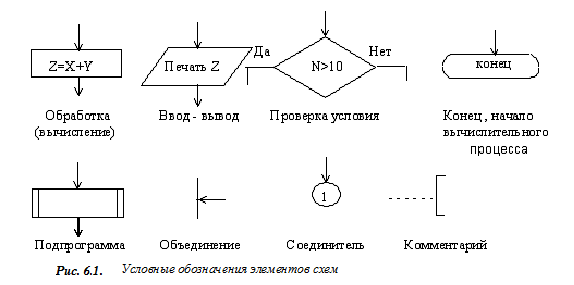 |
вычисления). Следовательно, термины «переменная» или «функция» только условно соответствуют общепринятым математическим понятиям. Числа, используемые, например, в операторах присваивания для задания значений переменных, называются константами. Константы обозначают сами числа, а не фактические адреса ячеек памяти.
Оператор присваивания, обсуждающийся в этом разделе, используется только для выполнения арифметических операций, поэтому он называется арифметическим оператором присваивания. В языках программирования имеются и другие виды операторов присваивания. Арифметический оператор присваивания выполняет следующие действия. Операции, указанные справа от символа «=», выполняются над записанными в выражении константами (константа — величина, значение которой не изменяется в период ее существования) и теми числами, которые хранятся в ячейках памяти, обозначенных встречающимися именами. Результат помещается в ту ячейку памяти, символический адрес которой указан слева от символа «=». Говорят, что переменной присваивается значение посредством оператора присваивания. Следовательно, используемый здесь символ «=» (присвоить) имеет смысл, отличный от принятого в математике.
В операторах присваивания справа от знака “=“ часто используются арифметические выражения.
Арифметическим выражениемназывается математическая запись, состоящая из констант, переменных, стандартных и нестандартных функций, объединённых знаками арифметических операций:
При записи арифметических выражений используются также круглые скобки. Порядок выполнения действий такой же, как в математике.
Примеры операторов присваивания
| Оператор присваивания | Действие оператора |
| К=1 | В ячейку памяти с символическим адресом К помещается 1. (переменной К присваивается значение 1) |
| L=K | В ячейку памяти с символическим адресом L пересылается содержимое ячейки с символическим адресом К (переменной L присваивается значение К). При этом К не изменяется. |
| К=К+1 | К содержимому ячейки с символическим адресом К прибавляется 1, результат помещается в ту же ячейку К. При этом старое значение К пропадает (стирается). |
| Y=SIN(X) | Вычисляется sin угла (выраженного в радианах), величина которого находится в ячейке Х, и результат помещается в ячейку Y. |
| X=SIN(X) | Правая часть вычисляется аналогично. Значение функции записывается в ту же ячейку, в которой раньше находилось значение угла. Перед присваиванием старое значение пропадает (стирается). |
Замечания:
1. Перед выполнением присваивания старое значение стирается.
2. При пересылке значение переменной копируется. Значение копируемой переменной не изменяется.
З. Переменным, которые располагаются в правой части оператора присваивания, должны быть присвоены определенные значения предшествующими операторами.
4. Если переменной не присвоено значение, то ее значение не определено.
Проверка условия. Проверка условия является основой организации разветвлений, т. е. выбора одного из двух (или более) путей вычислительного процесса. Это этап принятия решения о дальнейшем ходе вычислительного процесса в зависимости от полученных промежуточных результатов. Имеется три вида разветвлений (см. ниже).
Ввод-вывод данных. В операторах ввода-вывода записываются имена тех переменных, значения которых должны вводиться в оперативную память или выводиться из нее. В этих операторах могут быть указаны также внешние устройства, с которыми осуществляется обмен информацией. При вводе данные записываются в те ячейки памяти, символические адреса (имена) которых указаны в операторе. При выводе (печати) данных на экране (или бумаге) появляются значения, находящиеся в ячейках памяти, символические адреса которых перечислены в операторе вывода.
Подпрограмма. Группу операторов, которые решают логически самостоятельную часть задачи, можно объединить в подпрограмму. Подпрограммы подробно рассматриваются ниже.
Соединительные линии и их объединение.Все блоки схемы соединяются посредством линий, которые в сомнительных случаях снабжаются направляющими стрелками. Основными являются направления сверху вниз и слева направо. Объединение нескольких ветвей в одну ветвь обозначается точкой. Пересекающиеся линии без обозначения точки пересечения означают отсутствие соединений. По возможности следует избегать пересечений.
Точками связи, или соединителями, пользуются в том случае, если соединительная линия не может быть доведена до следующего блока или до точки объединения. Тогда линия оканчивается соединителем, в котором записывается любой символ. Продолжением этой линии считается вторая точка связи, помеченная тем же символом.
Комментарии можно записывать около любого блока.
В настоящее время существует технология разработки программ без использования схем. Однако независимо от этого на начальном этапе изучения программирования использование схем при разработке алгоритма целесообразно. Использование схем обеспечивает приобретение прочных навыков разработки алгоритмов с использованием типовых структур алгоритмов, являющихся основой так называемого структурного подхода, особенно плодотворного при постановке и решении на ЭВМ сложных задач.
ГОСТ помимо типов фигур предписывает также определенные размеры их сторон, одинаковые размеры блоков. Этих требований необходимо придерживаться при оформлении окончательной документации. На промежуточных этапах разработки алгоритма придерживаться этих требований ГОСТа не обязательно.
Процесс математического моделирования
Отличительной особенностью математических моделей, создаваемых в настоящее время, является их комплексность, связанная со сложностью моделируемых объектов. Это приводит к усложнению модели и необходимости совместного использования нескольких теорий из разных областей знания, применения современных вычислительных методов и вычислительной техники для получения и анализа результатов моделирования. В случае сложных объектов удовлетворить всем предъявляемым требованиям в одной модели обычно невозможно. Приходится создавать целый спектр моделей одного и того же объекта (в некоторых случаях — иерархическую совокупность «вложенных» одна в другую моделей), каждая из которых наиболее эффективно решает возложенные на нее задачи.
Необходимость массового построения моделей требует разработки некоторой совокупности правил и подходов, которые позволили бы снизить затраты на разработку моделей и уменьшить вероятность появления трудно устранимых впоследствии ошибок. Подобную совокупность правил можно было бы назвать технологией создания математических моделей.
Процесс построения любой математической модели можно представить последовательностью этапов:
Обследование объекта моделирования
Математические модели, особенно использующие численные методы и вычислительную технику, требуют для своего построения значительных интеллектуальных, финансовых и временных затрат. Поэтому решение о разработке новой модели принимается лишь в случае отсутствия иных, более простых путей решения возникших проблем (например, модификации одной из существующих моделей).
Необходимость в новой модели может появиться в связи с проведением научных исследований, особенно — на стыке различных областей знания. После принятия решения о необходимости построения новой математической модели заказчик ищет исполнителя своего заказа. В качестве исполнителя, как правило, может выступать рабочая группа, включающая специалистов разного профиля: прикладных математиков, специалистов, хорошо знающих особенности объекта моделирования, программистов. Если решение о создании модели принято и рабочая группа сформирована, то приступают к этапу обследования объекта моделирования. Основной целью данного этапа является подготовка содержательной постановки задачи моделирования. Перечень сформулированных в содержательной (словесной) форме основных вопросов об объекте моделирования, интересующих заказчика, составляет содержательную постановку задачи моделирования.
Подготовка списка вопросов, на которые должна ответить новая модель, зачастую является самостоятельной проблемой, требующей для своего решения специалистов со специфическими знаниями и способностями. Они должны не только хорошо разбираться в предметной области моделирования, знать возможности современной вычислительной математики и техники, но и уметь общаться с людьми, «разговорить» практиков, хорошо «чувствующих» объект моделирования, нюансы его поведения. К таким специалистам например относят системных аналитиков, системных инженеров, специалистов по исследованию операций.
На основании анализа всей собранной информации постановщик задачи должен сформулировать такие требования к будущей модели, которые, с одной стороны, удовлетворяли бы заказчика, а с другой — позволяли бы реализовать модель в заданные сроки и в рамках выделенных материальных средств. Системные аналитики (или операционисты) должны обладать способностью из большого объема слабо формализованной разнообразной информации об объекте моделирования, из различных нечетко высказанных и сформулированных пожеланий и требований заказчика к будущей модели выделить то главное, что может быть действительно реализовано.
На основе собранной информации об объекте моделирования системный аналитик (инженер, операционист) совместно с заказчиком формулируют содержательную постановку задачи моделирования, которая, как правило, не бывает окончательной и может уточняться и конкретизироваться в процессе разработки модели. Однако, все последующие уточнения и изменения содержательной постановки должны носить частный, не принципиальный характер.
Весь собранный в результате обследования материал о накопленных к данному моменту знаниях об объекте, содержательная постановка задачи моделирования, дополнительные требования к реализации модели и представлению результатов оформляются в виде технического задания на проектирование и разработку модели. Техническое задание является итоговым документом, заканчивающим этап обследования. Чем более полную информацию удастся собрать об объекте на этапе обследования, тем более четко можно выполнить содержательную постановку задачи, более полно учесть накопленный опыт и знания, избежать многих сложностей на последующих этапах разработки модели.
Концептуальная постановка задачи моделирования
В отличие от содержательной концептуальная постановка задачи моделирования, как правило, формулируется членами рабочей группы без привлечения представителей заказчика, на основании разработанного на предыдущем этапе технического задания, с использованием имеющихся знаний об объекте моделирования и требований к будущей модели. Анализ и совместное обсуждение членами рабочей группы всей имеющейся информации об объекте моделирования позволяет сформировать содержательную модель объекта, являющуюся синтезом когнитивных моделей, сложившихся у каждого из членов рабочей группы.
Концептуальная постановка задачи моделирования — это сформулированный в терминах конкретных дисциплин перечень основных вопросов, интересующих заказчика, а также совокупность гипотез относительно свойств и поведения объекта моделирования.
Наибольшие трудности при формулировке концептуальной постановки приходится преодолевать в моделях, находящихся на «стыке» различных дисциплин. Различия традиций, понятий и языков, используемых для описания одних и тех же объектов, являются очень серьезными препятствиями, возникающими при создании «междисциплинарных» моделей.
Математическая постановка задачи
Законченная концептуальная постановка позволяет сформулировать математическую постановку задачи моделирования, включающую совокупность различных математических соотношений, описывающих поведение и свойства объекта моделирования.
Математическая постановка задачи моделирования — это совокупность математических соотношений, описывающих поведение и свойства объекта моделирования.
Математическая модель является корректной, если для нее осуществлен и получен положительный результат всех контрольных проверок: размерности, порядков, характера зависимостей, экстремальных ситуаций, граничных условий, предметного смысла и математической замкнутости. Математическая постановка задачи еще более абстрактна, чем концептуальная, так как сводит исходную задачу к чисто математической, методы решения которой достаточно хорошо разработаны.
Выбор и обоснование выбора решения задачи
Все методы решения задач, составляющих «ядро» математических моделей, можно подразделить на аналитические и алгоритмические.
Следует отметить, что при использовании аналитических решений для получения результатов «в числах» также часто требуется разработка соответствующих алгоритмов, реализуемых на вычислительной технике.
Однако исходное решение при этом представляет собой аналитическое выражение (или их совокупность). Решения же, основанные на алгоритмических методах, принципиально не сводимы к точным аналитическим решениям рассматриваемой задачи.
Выбор того или иного метода исследования в значительной степени зависит от квалификации и опыта членов рабочей группы. Аналитические методы более удобны для последующего анализа результатов, но применимы лишь для относительно простых моделей. В случае, если математическая задача (хотя бы и в упрощенной постановке) допускает аналитическое решение, последнее, без сомнения, предпочтительнее численного.
Алгоритмические методы сводятся к некоторому алгоритму, реализующему вычислительный эксперимент с использованием вычислительной техники. Точность моделирования в подобном эксперименте существенно зависит от выбранного метода и его параметров. Алгоритмические методы, как правило, более трудоемки в реализации, требуют от членов рабочей группы хорошего знания методов вычислительной математики, обширной библиотеки специального программного обеспечения и мощной вычислительной техники.
Численные методы применимы лишь для корректных математических задач, что существенно ограничивает использование их в математическом моделировании. Общим для всех численных методов является сведение математической задачи к конечномерной. Это чаще всего достигается дискретизацией исходной задачи, то есть переходом от функции непрерывного аргумента к функциям дискретного аргумента. Применение любого численного метода неминуемо приводит к погрешности результатов решения задачи. Выделяют три основных составляющих возникающей погрешности при численном решении исходной задачи: неустранимая погрешность, связанная с неточным заданием исходных данных (начальные и граничные условия, коэффициенты и правые части уравнений); погрешность метода, связанная с переходом к дискретному аналогу исходной задачи; ошибка округления, связанная с конечной разрядностью чисел, представляемых в вычислительной машине.
Естественным требованием для конкретного вычислительного алгоритма является согласованность в порядках величин перечисленных трех видов погрешностей.
Численный, или приближенный, метод реализуется всегда в виде вычислительного алгоритма. Поэтому все требования, предъявляемые к алгоритму, применимы и к вычислительному алгоритму. Прежде всего, алгоритм должен быть реализуем — обеспечивать решение задачи за допустимое машинное время. Важной характеристикой алгоритма является его точность, то есть возможность получения решения исходной задачи с заданной точностью за конечное число действий.
Время работы алгоритма зависит от числа действий, необходимых для достижения заданной точности. Для любой математической задачи, как правило, можно предложить несколько алгоритмов, позволяющих получить решение с заданной точностью, но за разное число действий. Алгоритмы, включающие меньшее число действий для достижения одинаковой точности, называют более экономичными, или более эффективными.
В процессе работы вычислительного алгоритма на каждом акте вычислений возникает некоторая погрешность. При этом от действия к действию она может возрастать или не возрастать (а в некоторых случаях даже уменьшаться). Если погрешность в процессе вычислений неограниченно возрастает, то такой алгоритм называется неустойчивым, или расходящимся. В противном случае алгоритм называется устойчивым, или сходящимся.
Огромное разнообразие численных методов в значительной степени затрудняет выбор того или иного метода в каждом конкретном случае. Поскольку для реализации одной и той же модели можно использовать несколько альтернативных алгоритмических методов, то выбор конкретного метода производится с учетом того, какой из них больше подходит для данной модели с точки зрения обеспечения эффективности, устойчивости и точности результатов, а также более освоен и знаком членам рабочей группы.
Реализация математической модели в виде компьютерной программы
При создании различных программных комплексов, используемых для решения разнообразных исследовательских, проектно-конструкторских и управленческих задач, в настоящее время, основой, как правило, служат математические модели. В связи с этим возникает необходимость реализации модели в виде компьютерной программы. Процесс разработки надежного и эффективного программного обеспечения является не менее сложным, чем все предыдущие этапы создания математической модели. Успешное решение данной задачи возможно лишь при уверенном владении современными алгоритмическими языками и технологиями программирования, знаний возможностей вычислительной техники, имеющегося программного обеспечения, особенностей реализации методов вычислительной математики.
Процесс создания программного обеспечения можно разбить на несколько этапов:
Техническое задание на разработку программного обеспечения оформляют в виде спецификации. На этапе проектирования формируется общая структура программного комплекса. Вся программа разбивается на программные модули. Для каждого программного модуля формулируются требования по реализуемым функциям и разрабатывается алгоритм, выполняющий эти функции. Определяется схема взаимодействия программных модулей, называемая схемой потоков данных программного комплекса. Разрабатывается план и задаются исходные данные для тестирования отдельных модулей и программного комплекса в целом.
Большинство программ, реализующих математические модели, состоят из трех основных частей:
Большое значение следует придавать освоению современных технологий программирования. Назначение любой технологии — это в первую очередь повышение надежности программного обеспечения и увеличение производительности труда программиста. Причем чем серьезней и объемней программный проект, тем большее значение приобретают вопросы использования современных технологий программирования. Пренебрежение данными вопросами может привести к значительным временным издержкам и снижению надежности программного комплекса.
Важнейшим фактором, определяющим надежность и малые сроки создания программного комплекса для решения конкретного класса задач, является наличие развитой библиотеки совместимых между собой программных модулей. Программа получается более надежной и создается за меньшие сроки при максимальном использовании стандартных программных элементов.
Проверка адекватности модели
Проверка адекватности модели преследует две цели:
Проверка разработанной математической модели выполняется путем сравнения с имеющимися экспериментальными данными о реальном объекте или с результатами других, созданных ранее и хорошо себя зарекомендовавших моделей. В первом случае говорят о проверке путем сравнения с экспериментом, во втором — о сравнении с результатами решения тестовой задачи.
Решение вопроса о точности моделирования зависит от требований, предъявляемых к модели, и ее назначения. При этом должна учитываться точность получения экспериментальных результатов или особенности постановок тестовых задач. В моделях, предназначенных для выполнения оценочных и прикидочных расчетов, удовлетворительной считается точность 10-15%. В моделях, используемых в управляющих и контролирующих системах, требуемая точность может быть 1-2% и даже более.
При возникновении проблем, связанных с адекватностью модели, ее корректировку требуется начинать с последовательного анализа всех возможных причин, приведших к расхождению результатов моделирования и результатов эксперимента. В первую очередь требуется исследовать модель и оценить степень ее адекватности при различных значениях варьируемых параметров (начальных и граничных условиях, параметров, характеризующих свойства объектов моделирования). Если модель неадекватна в интересующей исследователя области параметров, то можно попытаться уточнить значения констант и исходных параметров модели. Если же и в этом случае нет положительных результатов, то единственной возможностью улучшения модели остается изменение принятой системы гипотез. Данное решение фактически означает возвращение ко второму этапу процесса разработки модели и может повлечь не только серьезное изменение математической постановки задачи, но и методов ее решения (например, переход от аналитических к численным), полной переработки программного обеспечения и нового цикла проверки модели на адекватность. Поэтому решение об изменении принятой системы гипотез должно быть всесторонне взвешено и приниматься только в том случае, если исчерпаны все прочие возможности по улучшению адекватности модели.
Практическое использование модели и анализ результатов моделирования
Дескриптивные модели, предназначены для описания исследуемых параметров некоторого явления или процесса, а также для изучения закономерностей изменения этих параметров. Эти модели могут использоваться для изучения свойств и особенностей поведения исследуемого объекта при различных сочетаниях исходных данных и разных режимах; при построении оптимизационных моделей и моделей-имитаторов сложных систем.
Модели, разрабатываемые для исследовательских целей, как правило, не доводятся до уровня программных комплексов, предназначенных для передачи сторонним пользователям. Время их существования чаще всего ограничено временем выполнения исследовательских работ по соответствующему направлению. Эти модели отличает поисковый характер, применение новых вычислительных процедур и алгоритмов, неразвитый программный интерфейс.
Модели и построенные на их основе программные комплексы, предназначенные для последующей передачи сторонним пользователям или коммерческого распространения, имеют развитый дружественный интерфейс, мощные пре- и постпроцессоры. Данные модели обычно строятся на апробированных и хорошо себя зарекомендовавших постановках и вычислительных процедурах. Однако следует помнить, что такие модели предназначены только для решения четко оговоренного класса задач.
Независимо от области применения созданной модели группа разработчиков обязана провести качественный и количественный анализ результатов моделирования.
Работая с моделью, разработчики становятся специалистами в области, связанной с объектом моделирования. Они достаточно хорошо представляют свойства объекта, могут предсказать и объяснить его поведение.
Поэтому всесторонний анализ результатов моделирования позволяет: