Что такое логический закон
ЛОГИЧЕСКИЙ ЗАКОН
Полезное
Смотреть что такое «ЛОГИЧЕСКИЙ ЗАКОН» в других словарях:
логический закон — ЛОГИЧЕСКИЙ ЗАКОН общее название законов, образующих основу логической дедукции. Понятие о Л. з. восходит к древнегреч. понятию о логосе как о предпосылке объективной («природной») правильности рассуждений. Собственно логическое содержание … Энциклопедия эпистемологии и философии науки
ЛОГИЧЕСКИЙ ЗАКОН — название законов, образующих основу логической дедукции; схема логической связи высказываний, выражаемая общезначимой формулой логики (аксиомой или теоремой), убедительность которой вытекает из одного только истолкования входящих в нее логических … Большой Энциклопедический словарь
логический закон — название законов, образующих основу логической дедукции; схема логической связи высказываний, выражаемая общезначимой формулой логики (аксиомой или теоремой), убедительность которой вытекает из одного только истолкования входящих в неё логических … Энциклопедический словарь
логический закон — выражение, содержащее только логические константы и переменные и явля ющееся истинным в любой (непустой) предметной области. Примером Л. з. может служить любой закон логики высказываний (скажем, непротиворечия закон, закон исключенного третьего,… … Словарь терминов логики
Логический закон — общее название законов, образующих основу логической дедукции. Понятие о Л. з. восходит к древнегреческому понятию о lógos e как предпосылке объективной («природной») правильности рассуждений. Собственно логическое содержание оно впервые… … Большая советская энциклопедия
ЛОГИЧЕСКИЙ ЗАКОН — в математической логике логическая формула, к рая является схемой истинных предложений, т. е. превращается в истинное высказывание при любой интерпретации входящих в нее переменных для высказываний и предикатов. Такие формулы наз. общезначимыми,… … Математическая энциклопедия
ЗАКОН ЛОГИЧЕСКИЙ — ЗАКОН ЛОГИЧЕСКИЙ общее название законов, образующих основу логической дедукции. Понятие о законах логики восходит к древнегреческому понятию о logos e как предпосылке объективной (“природной”) правильности рассуждений. Собственно логическое… … Философская энциклопедия
закон клавия — логический закон, характеризующий связь импликации ( если, то ) и отрицания. Его можно передать так: если из отрицания некоторого высказывания вытекает само это высказывание, то оно является истинным. Или короче: высказывание, вытекающее из… … Словарь терминов логики
ЗАКОН ТОЖДЕСТВА — логический закон, согласно которому всякое высказывание влечет (имплицирует) само себя. Внешне это самый простой из логических законов. Его можно передать так: если высказывание истинно, то оно истинно. Напр.: «Если трава зеленая, то она зеленая» … Философская энциклопедия
Закон противоречия — Закон непротиворечия (закон противоречия) закон логики, который гласит, что два несовместимых (противоречащих либо противоположных) суждения не могут быть одновременно истинными. По крайней мере, одно из них необходимо ложно[1].… … Википедия
4 закона логики
В поле зрения логики как науки о познавательной деятельности пребывают не только формы мышления, но и отношения, возникающие между ними в мыслительном процессе. Дело в том, что не каждая совокупность понятий, суждений, умозаключений дает возможность построить эффективное размышление. Для него обязательными атрибутами являются последовательность, непротиворечивость, обоснованная связь. Эти аспекты, необходимые для эффективных размышлений, призваны обеспечить логические законы.
Логические законы
Чтобы избежать искаженного представления о предмете статьи, укажем, что, говоря об основных законах логики, мы имеем в виду законы формальной логики (тождества, непротиворечия, исключенного третьего, достаточного основания), а не логики предикатов.
Логический закон – внутренняя существенная, необходимая связь между логическими формами в процессе построения размышления. Под логическим законом Аристотель, который, к слову, первым сформулировал три из четырех законов формальной логики, подразумевал предпосылку к объективной, «природной» правильности рассуждения.
Многие учебные материалы часто предлагают следующие формулы для записи основных законов логики:
Стоит помнить, что такое обозначение во многом условно и, как отмечают ученые, не всегда в полной мере способны раскрыть суть самих законов.
1. Закон тождества
Аристотель в своей «Метафизике» указывал на тот факт, что размышление невозможно «если не мыслить каждый раз что-нибудь одно». Большинство современных учебных материалов закон тождества формулирует так: «Любое высказывание (мысль, понятие, суждение) на протяжении всего рассуждения должно сохранять один и тот же смысл».
Отсюда следует важное требование: запрещается тождественные мысли принимать за различные, а различные – за тождественные. Поскольку естественный язык позволяет выражать одну и ту же мысль через различные языковые формы, то это может стать причиной подмены исходного смысла понятий и к замене одной мысли другой.
Чтобы подтвердить закон тождества Аристотель обратился к анализу софизмов – ложных высказываний, которые при поверхностном рассмотрении кажутся правильными. Наиболее известные софизмы, наверное, слышал каждый. Например: «Полупустое есть то же, что и наполовину полное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное» или «6 и 3 есть четное и нечетное. 6 и 3 есть девять. Следовательно, 9 есть и четное, и нечетное».
Внешне форма рассуждения правильная, но при анализе хода рассуждения обнаруживается ошибка, связанная с нарушением закона тождества. Так, во втором примере всем понятно, что число 9 не может быть одновременно и четным, и нечетным. Ошибка в том, что союз «и» в условии употребляется в разных значениях: в первом как объединение, одновременная характеристика чисел 6 и 3, а во втором – как арифметическое действие сложения. Отсюда и ошибочность вывода, ведь в процессе рассуждения к предмету были применены разные смыслы. По сути, закон тождества – требование в определенности и неизменности мыслей в процессе рассуждения.
Извлекая будничный смысл из вышесказанного остановимся на понимании того, к чему относится закон тождества. В соответствии с ним всегда стоит помнить, что прежде чем приступить к обсуждению любого вопроса, нужно четко определить его содержание и неизменно ему следовать, не смешивая понятий и избегая двусмысленностей.
Закон тождества не предполагает, что вещи, явления и понятия неизменны в некоторых моментах, он основывается на том, что мысль, зафиксированная в определенном языковом выражении, несмотря на все возможные преобразования, должна оставаться тождественной сама себе в пределах конкретного соображения.
2. Закон непротиворечия (противоречия)
Формально-логический закон непротиворечия основывается на доводе, что два несовместимых друг с другом суждения не могут быть одновременно истинными; как минимум одно из них ложно. Оно вытекает из понимания содержания закона тождества: в одно время, в одном отношении истинными не могут быть два суждения о предмете, если одно из них что-нибудь утверждает о нем, а второе это же отрицает.
Сам Аристотель писал: «Невозможно, чтобы одно и то же одновременно было и не было присуще одному и тому же, в одном и том же смысле».
Разберемся с этим законом на конкретном примере – рассмотрим следующие суждения:
Для того, чтобы определить какое высказывание истинно, обратимся к логике. Можем утверждать, что одновременно оба высказывания быть правдивыми не могут, поскольку являются противоречивыми. Из этого следует, что если доказать истинность одного из них, то второе обязательно будет ошибочным. Если же доказать ошибочность одного, то второе может быть как истинным, так и неправдивым. Чтобы узнать правду, исходные данные достаточно проверить, например, с помощью метрики.
По сути, этот закон запрещает утверждать и отрицать одно и то же одновременно. Внешне закон противоречия может показаться очевидным и вызвать справедливое сомнение по поводу целесообразности выделения столь простого вывода в логический закон. Но здесь есть свои нюансы и связаны они с природой самих противоречий. Так, контактные противоречия (когда что-либо утверждается и отрицается почти в одно и то же время, например, уже следующим предложением в речи) более чем очевидны и практически не встречаются. В отличие от первой разновидности, дистантные противоречия (когда между противоречивыми суждениями находится значительный интервал в речи или тексте) – более распространенные и их нужно избегать.
Чтобы эффективно использовать закон противоречия достаточно правильно учитывать условия его употребления. Основным требованием является соблюдение в высказываемой мысли единства времени и отношения между предметами. Другими словами, нарушением закона непротиворечия не может считаться утвердительное и отрицательное суждения, которые относятся к разному времени или употребляются в разных отношениях. Приведем примеры. Так, высказывания «Москва – столица» и «Москва – не столица» могут быть одновременно правильными, если мы говорим в первом случае о современности, а во втором – об эпохе Петра I, который, как известно, перенес столицу в Санкт-Петербург.
В плане разности отношений истинность противоречивых суждений можно передать на таком примере: «Моя подруга хорошо владеет испанским языком» и «Моя подруга плохо владеет испанским языком». Оба утверждения могут быть истинны, если в момент речи в первом случае говорится об успехах в изучении языка по университетской программе, а во втором о возможности работы профессиональным переводчиком.
Таким образом, закон противоречия фиксирует отношения между противоположными суждениями (логическими противоречиями) и никаким образом не касается противоположных сторон одной сущности. Его знание необходимо для дисциплины процесса мышления и исключения возможных неточностей, которые возникают в случае нарушения.
3. Закон исключенного третьего
Намного «знаменитей», чем предыдущие два закона Аристотеля, в широких кругах, благодаря значительной распространенности сентенции «tertium non datur», что в переводе значит «третьего не дано» и отображает суть закона. Закон исключенного третьего – требование к мыслительному процессу, согласно с которым если в одном из двух выражений что-либо о предмете утверждается, а во втором отрицается – одно из них обязательно истинно.
Аристотель в Книге 3 «Метафизики» писал: «…ничего не может быть посредине между двумя противоречивыми суждениями об одном, каждый отдельный предикат необходимо либо утверждать, либо отрицать». Древнегреческий мудрец отмечал, что закон исключенного третьего применим лишь в случае высказываний, употребленных в прошедшем или настоящем времени и не работает с будущим временем, ведь нельзя сказать с достаточной долей уверенности произойдет или не произойдет что-либо.
Очевидно, что закон непротиворечия и закон исключенного третьего тесно связаны. Действительно, те суждения, которые подходят под действие закона исключенного третьего, подходят и под закон непротиворечия, но не все суждения последнего, попадают под действие первого.
Закон исключенного третьего применим к таким формам суждений:
Одно суждение утверждает что-либо о предмете в одном и том же отношении в одно время, а второе – то же самое отрицает. Например: «Страусы – птицы» и «Страусы – не птицы».
Одно суждение утверждает что-либо относительно всего класса предметов, второе – отрицает это же, но относительно лишь некоторой части предметов. Например: «Все учащиеся группы ИН-14 сдали сессию на отлично» и «Некоторые учащиеся группы ИН-14 не сдали сессию на отлично».
Одно суждение отрицает характеристику класса предметов, а второе эту же характеристику утверждает в отношении некоторой части предметов. Пример: «Ни один житель нашего дома не пользуется Интернетом» и «Некоторые жители нашего дома пользуются Интернетом».
Позже, начиная с эпохи Нового времени, закон был раскритикован. Известная формулировка, применявшаяся для этого: «Насколько верно утверждать, что все лебеди черные, исходя из того, что нам до сих пор встречались только черные?». Дело в том, что закон применим лишь в аристотелевской двузначной логике, которая основывается на абстракции. Поскольку ряд элементов бесконечен, проверить все альтернативы в подобного рода суждениях очень сложно, здесь требуется применение других логических принципов.
4. Закон достаточного основания
Четвертый из основных законов формальной или классической логики был сформулирован по прошествии значительного периода времени после обоснования Аристотелем первых трех. Его автор – видный немецкий ученый (философ, логик, математик, историк; этот список занятий можно продолжить) – Готфрид Вильгельм Лейбниц. В своей работе о простых субстанциях («Монадология», 1714 г.) он писал: «…ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, – без достаточного основания, почему именно дело обстоит так, а не иначе, хотя эти основания в большинстве случаев вовсе не могут быть нам известны».
Современное определение закона Лейбница основано на понимании, что всякое положение для того, чтобы считаться вполне достоверным, должно быть доказанным; должны быть известны достаточные основания, в силу которых оно считается истинным.
Функциональное предназначение данного закона выражается в требовании соблюдать в мышлении такую черту, как обоснованность. Г. В. Лейбниц, по сути, объединил законы Аристотеля с их условиями определенности, последовательности и непротиворечивости рассуждения, и на основании этого разработал понятие о достаточном основании для того, чтоб характер размышления был логичным. Немецкий логик хотел этим законом показать, что в познавательной или практической деятельности человека рано или поздно наступает момент, когда недостаточно иметь просто истинное утверждение, нужно чтобы оно было обоснованным.
При детальном анализе оказывается, что закон достаточного основания мы применяем в повседневной жизни довольно часто. Делать выводы, основываясь на фактах – значит применять этот закон. Школьник, указывающий в конце реферата список использованной литературы и студент, оформляющий ссылки на источники в курсовой работе – этим они подкрепляют свои выводы и положения, следовательно, используют закон достаточного основания. С тем же самым люди разных профессий сталкиваются в процессе своей работы: доцент – при поиске материала для научной статьи, спичрайтер – при написании речи, прокурор – во время подготовки обвинительного выступления.
Нарушение закона достаточного основания также широко распространено. Иногда причиной тому неграмотность, иногда – специальные уловки с целью получения выгоды (например, построение аргументации с нарушением закона для победы в споре). Как пример, высказывания: «Этот человек не болеет, у него ведь нет кашля» или «Гражданин Иванов не мог совершить преступление, ведь он прекрасный работник, заботливый отец и хороший семьянин». В обоих случаях ясно, что приводимые аргументы в недостаточной мере обосновывают тезис, а, значит, являются прямым нарушением одного из основных законов логики – закона достаточного основания.
Интересуетесь развитием логического мышления и мышления глобально? Обратите внимание на курс «Когнитивистика»».
Отзывы и комментарии
Поделиться своими знаниями в области законов классической логики, порекомендовать литературу для детального ознакомления с ними, а также обсудить данную статью вы можете путем добавления комментария в специальное поле ниже.
Законы логики, которые должны знать все
Все мы хотим понять, что правильно, а что нет. Так, фраза «это нелогично» стала чуть ли не самой используемой при критике какого-нибудь сериала или фильма. Но вот о том, что такое логика и как вообще различать, что логично, а что нет, — знают далеко не все. А ведь у неё как у раздела философии есть своё понятие и законы.
Логика по Аристотелю
Древние греки вообще любили рассуждать о том, как устроен наш мир и в чём его смысл. У них это, кстати, получалось вполне неплохо. Так, учёный и философ Левкипп и его ученик Демокрит открыли атомы, не имея при этом наших микроскопов. Сделать это им удалось в том числе благодаря логике.
В Античности очень часто пользовались рассуждениями об объекте для его познания. Строился этот принцип на том, что во Вселенной есть законы, которые человек способен понять через мысли и опыт.
Вот и Аристотель был парень не промах. Он вывел четыре основных закона логики и определил, что это наука, которая является вспомогательной для познания мира. Она изучает законы и форму мышления, ведь только структурировавший своё мышление учёный будет способен совершать открытия.
Первый закон: закон тождества
Суть первого закона в том, что у каждого слова должно быть одно определённое значение. Так как люди выражают информацию в основном при помощи слов, то от того, что мы понимаем под каждым словом, и зависит результат любого диалога, понимание книги, фильма, сериала и так далее. Без точного определения мы попросту не можем правильно выразить свои мысли.
Конечно, так же важен и сам контекст, в котором слово употребляется. Первый закон логики указывает именно на значение слова в один определённый момент в одном определённом месте. Ведь существуют такие слова, как «ключ», «шип» и прочие омонимы, понимание значения которых как раз и зависит от контекста.
Так, например, при нарушении закона логики на фразу «Мне не повезло: я сломал ногу в двух местах» можно было бы ответить: «Так не ходи в эти места», — так как понятие слова «место» заранее не было обговорено. Конечно, подобные мелочи мы редко замечаем в повседневной жизни, так как наше логическое мышление достаточно развито, чтобы находить правильные ответы на простые вопросы.
Второй закон: закон непротиворечивости
Этот закон еще называют законом правильного мышления. Его суть состоит в том, что высказывание и одновременное его отрицание не может быть истиной. Конечно, нужно отличать нарушение второго закона логики от игры слов. Так, обычная фраза строгих мам «закрой рот и ешь» нарушает второй закон, а вот фраза «в моём детстве у меня не было детства» — нет.
Третий закон логики: закон исключённого третьего
Если есть два противоположных суждения, когда одно из них отрицает другое, например А равно Б и А равно не Б, то не может быть иного суждения. Или в другой формулировке:
Если два суждения об одном предмете противоречат друг другу, то они не могут быть одновременно ложными или одновременно истинными. Важно отличать суждения противоречащие и противоположные.
Противоположное суждение может иметь третий вариант ответа. Если мы говорим: «Собака маленькая» и «Собака большая», — возможен третий вариант: «Собака средняя». А в противоречащем суждении мы можем сказать: «Эта собака небольшая» и «Эта собака большая». В этом случае верный ответ только один.
В реальной жизни этот закон применяется при обсуждении любых противоречивых тем. В результате такого диалога оба собеседника будут пытаться формулировать свою мысль так, чтобы она была логичной. Но при этом ответ на обсуждаемый вопрос всегда будет один, следовательно кто-то будет неправ, так как в своём суждении нарушает законы логики. Останется только определить, кто неправ.
Четвёртый закон логики: закон достаточного основания
Любые суждения, высказанные мысли, утверждения и так далее должны иметь твёрдые основания. Выдвинутое утверждение должно иметь достаточно аргументов, чтобы считаться истиной, и, следовательно, само вытекать из аргументов.
Являясь последним из законов, закон достаточного основания вобрал в себя предыдущие. Так как весь наш мир строится на наших суждениях о нём, важно, чтобы каждое суждение было обосновано. Верить во что-то без доказательств — это выбор глупцов, ведь недоказанное суждение стоит мало.
Конечно, для применения этого закона необходимо проверять каждое сомнительное суждение уже доказанными фактами. Так ты значительно уменьшаешь риск быть обманутым.
Урок 5. Логические законы и противоречия

Во введении к курсу было сказано, что логика – это нормативная наука о формах и приёмах рациональной познавательной деятельности. Как и любая другая наука, логика также формулирует свои законы. Однако в отличие от других наук, законы эти являются нормативными, то есть они не описывают процесс человеческого мышления, а предписывают, как человек должен мыслить, если он хочет, чтобы его рассуждение было корректным. Таким образом, логические законы представляют собой некие общие принципы, которыми люди должны руководствоваться в процессе рассуждения.
Если попытаться дать более строгое определение, то:
Логический закон – это определённая логическая форма, благодаря которой высказывание в целом принимает значение «истина», независимо от конкретного содержания его частей.
По этой причине логические законы также иногда называют логическими тавтологиями: о чём бы мы не говорили, высказывания, имеющие форму логических законов, всегда оказываются истинными. К тому же они кажутся «бесплодными», потому что мы не можем извлечь из них никакой реальной информации о мире.
Логические противоречия – полная противоположность логическим законам, то есть это такая логическая форма, при которой высказывание в целом всегда принимает значение «ложь», независимо от содержания его частей.
Содержание:
Таблицы истинности
Как же определить, что определённое высказывание всегда принимает значение «истина» или «ложь»? Логики придумали для этого очень удобный метод, который получил название «таблиц истинности». Как понятно из названия, они представляют собой таблицы, в которых в верхнюю строку записывается логическая форма высказываний, а в столбцы под каждым компонентом записываются их истинностные значения. Давайте построим таблицу истинности для высказывания «Идёт дождь».
Здесь всё довольно ясно: «Идёт дождь» – это простое высказывание, которое может принимать значение либо «истина», либо «ложь». Обычно для удобства логики сокращают значения до «и» и «л», а само высказывание записывают маленькой буквой латинского алфавита: p, q, r, s и т.д. Поэтому в классическом виде таблица истинности для одного простого высказывания будет выглядеть так:
Давайте теперь представим, что у нас есть два высказывания: «Идёт дождь» и «Светит солнце». Пока они никаким образом не связаны между собой. Однако поскольку их уже два, то у нас возможны уже не две, а четыре комбинации: оба высказывания истинны, оба высказывания ложны, истинно либо первое, либо второе высказывание. Таблица истинности для них будет включать уже четыре строки для значений.
Если у нас есть три высказывания («Идёт дождь», «Светит солнце», «Трава зеленеет»), то таблица будет включать уже восемь строк для значений, так как в таком случае возможны восемь комбинаций.
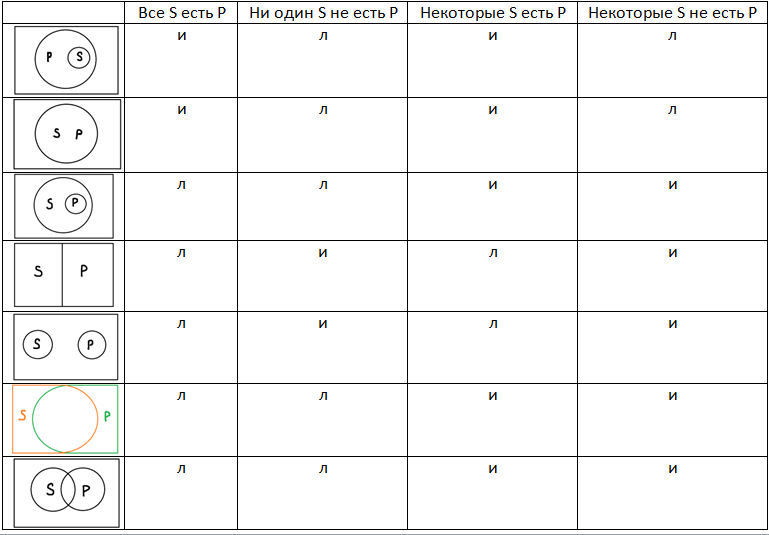
Таблицы истинности строятся и в силлогистике, однако выглядят они немного иначе. В левый столбец обычно помещается диаграмма, изображающая то или иное отношение между терминами S и P, а справа помещаются различные типы высказываний и их истинностные значения.
Это сводная таблица истинности для всех типов атрибутивных высказываний, которые мы обсуждали в прошлом уроке (единичные высказывания не включены отдельно, так как их условия истинности приравниваются к условиям истинности для общих высказываний).
Далее, понятно, что обычно в рассуждении высказывания каким-то образом связаны между собой с помощью пропозициональных связок. Мы зададим истинностные значения для основных связок, которые используются чаще всего в естественном языке.
Логическое отрицание используется, когда в высказывании отрицается наличие некоторой ситуации в мире, говорится об её отсутствии. Например, «Дождь не идёт», «Комната была небольшой», «Неправда, что они друзья». В логике обычно передается через выражения «неверно, что p» или просто «не-p».
Как видно из таблицы, если высказывание истинно, то его отрицание будет принимать значение «ложь», если же высказывание само по себе ложно, то – «истина». Предположим, что вместо p мы имеем высказывание «Маргарет Тэтчер была первой и на настоящий момент единственной женщиной-премьер-министром Великобритании». Это истинное высказывание. Соответственно, если взять его отрицание: «Маргарет Тэтчер не была первой и на настоящий момент единственной женщиной-премьер-министром Великобритании», то оно будет ложным. Если же взять высказывание «Все болезни от нервов», которое является ложным, то его отрицание «Неверно, что все болезни от нервов» будет истинным.
Конъюнкция представляет собой одновременное утверждение наличия двух ситуаций. В естественном языке она обычно передаётся союзами «и», «а», «но» и конструкциями типа «в то же время», «одновременно», «вместе» и т.д. Примеры конъюнкции можно увидеть в высказываниях «Пошёл дождь, и я спрятался под навес», «Витя хотел пойти в кино, а я хотел поиграть в футбол», «Белкин ждал директора целый час, но так и не дождался». Как видно, конъюнкция соединяет два или более простых высказываний в одно сложное.
Конъюнктивное высказывание может быть истинным, только если все его части истинны. Если хотя бы одно простое высказывание, входящее в её состав ложно, то тогда и конъюнкция в целом ложна. Пример истинной конъюнкции: «44-го президента США зовут Барак, а его жену – Мишель». Все следующие высказывания будут ложными: «44-го президента США зовут Барак, а его жену – Мэгги», «44-го президента США зовут Борат, а его жену – Мишель», «44-го президента США зовут Джон, а его жену – Элен».
Дизъюнкция утверждает, что хотя бы одна из двух или более ситуаций имеет место. В естественном языке она выражается словами «или» и «либо». Примеры дизъюнктивных высказываний: «Маша была замужем за Анатолием или за Николаем», «Он работает над проектом ИК-25 либо ПФ-40». Хотя это не так очевидно, как в случае с конъюнкцией, дизъюнкция также объединяет в одно сложное высказывание два или более простых высказывания. Если мы выявляем логическую форму, то правильной была бы запись: «Маша была замужем за Анатолием, или Маша была замужем за Николаем».
Из таблицы понятно, что дизъюнкция ложна, только когда все простые высказывания, входящие в её состав ложны. К примеру, ложным будет высказывание «Уганда находится в Центральной Америке или Западной Европе». Когда хотя бы одна из частей дизъюнкции истина, она в целом также будет истинной. Например, истинным является высказывание «Нот всего семь или шесть». При этом важно отметить, что выражение «хотя бы одна» подразумевает, что и обе части могут быть истинными. Иллюстрацией может служить следующее высказывание: «Велосипеды бывают двухколёсными или трёхколесными». Велосипеды бывают и такими, и другими, поэтому высказывание истинно. Однако нередки случаи, когда мы хотим указать, что лишь одна из альтернатив истинна, но никак не обе вместе. Рассмотрим высказывание «Картина “Герника” принадлежит кисти Пикассо или Тициана». Здесь либо одно, либо другое. Они даже не могли написать её вместе, так как жили в разных веках. В таких ситуациях говорят о строгой дизъюнкции, которая будет истинна исключительно при истинности одного из её членов. Обычно она выражается словами «либо, либо».
Материальная импликация – это связка, которая передаёт отношения причинно-следственной связи между высказываниями. Она выражается словами «если, то». «Если Люся – полная отличница, то и по математике у неё должна быть пятёрка». Смысл импликации состоит в том, что если первое простое высказывание верно, то и второе тоже будет верным.
Попробуем разобраться с этой таблицей. Проблема в том, что истинностные значения материальной импликации, в отличие от значений других пропозициональных связок, совсем не являются интуитивными. С первой строкой всё ясно: если первое высказывание верно, и второе высказывание верно, то импликация в целом тоже верна. Пример: «Если птицы улетают на юг, то, значит, наступила осень». Со второй строкой тоже всё более или менее понятно: если первое высказывание истинно, а второе ложно, то отношения следования между ними нет. Вспомните отрывок из «Золотого ключика», в котором Мальвина пытается научить Буратино арифметике:
– Предположим у вас в кармане два яблока, и некто забрал у вас одно из них. Сколько у вас останется яблок?
– Два.
– Но почему?
– Ведь я не отдам Некту яблоко, пусть он и дерись!
Рассуждения Буратино можно представить в виде высказывания «Если некто забрал одно из имеющихся у меня двух яблок, у меня всё равно осталось два яблока». Если первая часть истинна, то вторая, безусловно, ложна, а потому и импликация в целом ложна. Способностей к арифметике у Буратино, действительно, не было.
С последними двумя строчками дело обстоит сложнее. Проблема в том, что для них сложно придумать пример на естественном языке. Когда логики формулировали значение материальной импликации, они пользовались математическим примером. Они взяли высказывание «Для всякого числа верно, что если оно кратно 4, то оно кратно и двум». Если это высказывание верно для всякого числа, то оно должно быть верным и для любого конкретного числа: 5, 6, 8, 12 и т.д. Если подставить в высказывание 8, то получим: «если 8 кратно 4, то оно кратно и 2». Здесь и первая, и вторая части истинны. Мы получили первую строку. Если подставить число 6, «если 6 кратно 4, то оно кратно и 2», то мы получаем третью строку (первая часть ложна, а вторая истинна). Если подставить 5, «если 5 кратно 4, то 5 кратно и двум», то выходит последняя строка (обе части ложны). Однако мы всё же можем подобрать примеры для всех этих ситуации, поэтому импликация истинна. Но вот для второй строки пример подобрать нельзя: нет такого числа, которое было бы кратно 4, но некратно 2. Поэтому вторая строка ложна.
Итак, мы разобрали истинностные значения основных связок, теперь мы можем посмотреть, какие их комбинации приведут к тому, что высказывание подобной формы будет всегда истинным, независимо от его содержания, другими словами – будет логическим законом.
Логические законы
Сразу стоит оговориться, что логических законов довольно много. Кроме того, обычно они формулируются в рамках конкретной логической системы: логики высказываний, логики предикатов, силлогистики, модальной логики и т.д. То, что является законом в одной системе, совсем необязательно будет законом в другой системе. Однако существует несколько основных законов, которые будут верны в любой логической системе. О них мы и расскажем.
Закон тождества
Закон тождества обычно формулируется в виде формулы «А есть А» или «Если А, то А».
Проверим этот закон с помощью таблицы истинности. Во-первых, у нас всего одно выражение – А, поэтому таблица будет включать только две комбинации: А истинно и А ложно. Во-вторых, связка «Если …, то …» выступает как знак материальной импликации. Таким образом, мы должны взять первую и последнюю строку из таблицы для материальной импликации.
Истинностное значение импликации
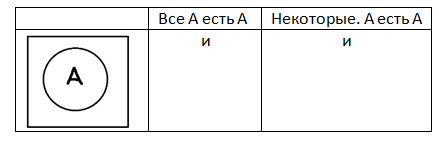
Закон тождества также может быть сформулирован и в силлогистике для высказываний «Все А есть А» и «Некоторые А есть А»:
Какой бы термин мы не подставили на место А, высказывания, имеющие эти формы, всегда будут истинными: «Все кошки – это кошки», «Все туфли – это туфли», «Некоторые автомобили – это автомобили», «Некоторые дома – это дома» и т.п.
Как понятно из названия этого закона, он говорит о том, что А тождественно самому себе. Что это означает? Смысл этого закона состоит в утверждении того, что языковые выражения (будь то термин или целое высказывание) не могут менять своё значение в процессе рассуждения. Языковые знаки должны трактоваться однозначно, их употребление должно быть стабильным. Если я утверждаю, что какое-то высказывание истинно, например, что высказывание «Красота спасёт мир» истинно, я не могу следующим шагом утверждать, что оно ложно. И наоборот, если я утверждаю, что какое-то высказывание ложно, оно не может вдруг ни с того ни с сего превратиться в истинное. Рассуждение должно быть последовательным.
Чаще всего закон тождества нарушается при так называемой подмене понятий: в ходе рассуждения используется один и тот же термин, но значения в него вкладываются каждый раз разные. К примеру, возьмём следующее рассуждение: «Знание – сила. Сила – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей. Следовательно, знание – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей». Такое рассуждение не может быть верным, так как здесь нарушен принцип тождества: термин «сила» употребляется в первом и втором предложении в разных значениях.
Закон противоречия
Закон противоречия гласит: неверно, что А и не-А.
Построим таблицу истинности.
В первом столбце даны значения А («истина» и «ложь»). Соответственно, мы просто копируем эти значения в третий столбец. Значения для не-А в пятом столбце будут прямо обратными для значений А, поэтому получаем «ложь», «истина». В четвёртом столбце располагается конъюнкция между А и не-А. Она не может быть истинной ни в одном из случаев. Поэтому её значение всегда «ложь». Наконец, второй столбец представляет значение выражения полностью – это отрицание конъюнкции между А и не-А. Поскольку конъюнкция ложна, то её отрицание будет истинным. В итоге, мы видим, что выражение в целом всегда истинно.
Если же мы возьмём выражение типа «А и не-А», то оно как раз будет представлять собой противоречие. Из таблицы мы видим, что такое выражение всегда будет принимать значение «ложь».
Согласно закону противоречия (иногда его называют законом непротиворечия) невозможно, чтобы одновременно оказались истинными высказывание и его прямое отрицание: неверно, что снег идёт и в то же время не идёт, неверно, что Катя любит ананасы и не любит ананасы. Важно сделать следующее замечание: противоречия возникает только тогда, когда утверждение и отрицание делаются об одном и том же объекте, в одно и то же время, в одном и тот же отношении. Например, высказывания «Снег идёт на Северном полюсе, но снег не идёт в Зимбабве», «Толя ходил в кино вчера, а сегодня не ходил», «Катя любит ананасы, а Петя не любит ананасы», «Вася любит кататься на коньках и не любит кататься на лыжах» не являются противоречиями. Все они говорят либо о разных предметах, либо о разных временных отрезках, либо о разных аспектах одного предмета. Поэтому не всё, что выглядит как противоречие, действительно является таковым. Такие кажущиеся противоречия называют мнимыми. Пример мнимого противоречия можно найти в дзенской притче «Бокудзю и ручей»:
Один дзэнский монах, Бокудзю, говорил: «Иди и пересеки ручей, но не позволяй воде прикоснуться к тебе».
А через ручей около его монастыря не было никакого моста. Многие пытались сделать это, но когда они пересекали ручей, то, конечно же, вода прикасалась к ним. Поэтому однажды один монах пришел к нему и сказал:
— Вы задали нам неразрешимую задачу. Мы пытаемся пересечь этот ручей; через него нет никакого моста. Если бы был мост, то мы, конечно же, пересекли бы ручей, и вода не прикоснулась бы к нам. Но мы вынуждены идти через поток, и вода прикасается к нам.
И Бокудзю сказал:
— Я пойду и пересеку его, а вы наблюдайте.
И Бокудзю пересёк ручей. Вода, конечно, прикоснулась к его ногам, и они сказали:
— Смотрите, вода прикоснулась к вам!
Бокудзю сказал:
— Насколько я знаю, она не прикоснулась ко мне. Я был просто свидетелем. Вода прикоснулась к моим ногам, но не ко мне. Я был просто свидетельствующим.
Между тем, чтобы пересечь ручей без моста и не позволить воде прикоснуться к себе, нет противоречия, потому что в данном случае человеческое я рассматривает в разных отношениях: как тело, и как дух. Тело проходит через ручей и намокает, но дух остаётся безмятежным и не затронутым водой.
Как и закон тождества, закон противоречия требует от нас быть последовательными в рассуждениях. Либо мы принимаем, что высказывание истинно, либо мы принимаем, что оно ложно, но не то и другое вместе. Смешение истины и лжи приводит к тому, что всё рассуждение обесценивается, так как мы уже не можем быть уверены в сделанном выводе. Противоречия опасны потому, что с точки зрения логики из них можно вывести всё что угодно, то есть высказывание формы «Если А и не-А, то В» всегда будет истинным. Вы можете сами проверить это с помощью таблицы истинности. «Если дождь идёт, и дождь не идёт, то Чехов – автор “Войны и мира”». Если допускать противоречия, подобное «рассуждение» оказывается возможным. Поэтому логика ставит запрет на противоречия.
Нужно сказать, что противоречия бывают не только явными, но и скрытыми. Очевидно, что чаще всего никто старается не допускать в своём рассуждении наличия двух прямо противоположных высказываний. Однако, не редки случаи, когда противоречие прячется за вроде бы правильными формулировками. Приведём несколько примеров, которые хорошо это иллюстрируют: «Мы заставим их стать свободными», «Мы будем бороться за мир, и камня на камне не останется от нашей борьбы». Понятно, что идея свободы предполагает, что человека не заставляют, а он сам принимает решения, а идея мира предполагает отсутствия борьбы или войны.
Обычно появление противоречия – это знак того, что в рассуждение где-то закралась ошибка. Исправление этой ошибки, снимет и противоречие. Ошибка может скрываться в сделанных умозаключениях, но может содержаться и в изначально избранных посылках. По этой причине приведение к противоречию играет ключевую роль в так называемых доказательствах от противного. Наверное, все помнят их со школьных уроков геометрии. Доказательство от противного строится на том, что нужно обосновать какой-то тезис, но прямое его доказательство найти не получается. Тогда берётся его отрицание, и в определённый момент рассуждения мы наталкиваемся на противоречие, а это знак того, что отрицание тезиса было неверным. Так что противоречие может играть и позитивную роль в рассуждении.
В заключение, добавим, что в советской философии, превозносившей Маркса и Гегеля, появилось целое направление под названием «диалектическая логика», которая якобы допускала наличие противоречий и даже оценивала их положительно. Такая точка зрения строилась на том, что противоречия – это источник движения и развития, а потому это хорошо, если мы сталкиваемся с ними. Ещё и сегодня можно встретить людей, которые придерживаются подобного мнения. Однако нужно понимать, что речь здесь не идёт о противоречии в логическом смысле (как форме высказывания, которое при любой интерпретации принимает значение «ложь»). Скорее, под противоречием тут следует мыслить несовместимость, плохую сочетаемость ситуаций, феноменов, характеров и т.д. Так во Франции конца XVIII века желание буржуазии участвовать в политической жизни страны плохо сочеталось с формой правления абсолютной монархии, что в итоге привело к буржуазной революции. Можно сказать, что между ними возникло противоречие, но это не имеет никакого отношения к логике.
Закон исключённого третьего
Закон исключённого третьего имеет следующую форму: А или неверно, что А.
Построим таблицу истинности:
Если А принимает значение «истина» и «ложь», то «неверно, что А» соответственно будет принимать значения «ложь» и «истина». Их дизъюнкция всегда будет истинной.
Закон исключённого третьего очень похож на закон противоречия, потому что он точно также утверждает, что высказывание и его отрицание не могут быть одновременно истинными. Истинно либо одно, либо другое, и третьего не дано. Истинно или высказывание «Глинка был композитором», или его отрицание «Глинка не был композитором», но они не могут быть истинными одновременно. Опять же здесь также стоит следить за тем, чтобы высказывания относились к одному и тому же предмету, говорили о нём в одном и том же отношении и в одно и то же время.
Нужно отметить, что законом исключённого третьего часто пользуются в качестве уловки, пытаясь представить какую-либо сложную ситуацию в виде простой оппозиции. К примеру: «Ты с нами или ты против нас», «Женщины бывают либо умными, либо красивыми», «Они либо патриоты, либо предатели». Особенно часто этим приёмом любят пользоваться политики, пытаясь представить, будто их оппоненты защищают какую-то радикальную позицию, которой те на самом деле не придерживаются. Отчасти эта склонность сводить всё многообразие фактов и позиций к двум противоположностям обусловлена чисто психологическими механизмами работы человеческого мышления. Всё дело в том, что наше мышление работает по так называемому принципу когнитивной экономии: вместо того, чтобы тратить время и энергию на анализ всей сложности ситуации, мы предпочитаем представить её в виде грубой полярной схемы. Поэтому если ваш собеседник или демагог из телевизора говорит вам, что «третьего не дано», подумайте, так ли это: не заключается ли между двумя членами оппозиции целый спектр разнообразных возможностей.
Кроме того, с законом исключённого третьего нужно быть аккуратными ещё и потому, что значения высказываний во многих случаях определяются относительно конкретного контекста. Помните Ивана и его детей из прошлого урока? Вполне можно было бы сказать в соответствии с законом исключённого третьего: «Дети Ивана либо лысы, либо нет, третьего не дано». Но ни одна из этих альтернатив не может нас удовлетворить, так как у Ивана нет детей. Таким образом, прежде чем применять закон исключённого третьего, сверьтесь с контекстом высказывания.
Законы тождества, противоречия и исключённого третьего фундаментальны и выполняются в любых логических системах. Без соблюдения этих законов невозможно делать правильные умозаключения. Иногда к ним присоединяют ещё так называемый закон достаточного основания. Этот закон гласит, что любое утверждение должно быть корректно обосновано. Хотя это очень важный принцип, на котором должны базироваться любые рассуждения, законом в собственно логическом смысле он не является, так как не представим в виде логической формы, которая при любой трактовке принимала бы значение «истина». Скорее, это общее требование, вытекающее из самой идеи логичного рассуждения, целью которого как раз и является обоснование тезиса путём правильных умозаключений. О том, как правильно делать умозаключения, мы начнём рассказывать в следующем уроке.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.