Что такое линейный угол

ЛИНЕЙНЫЙ УГОЛ

Смотреть что такое «ЛИНЕЙНЫЙ УГОЛ» в других словарях:

Линейный крейсер «Мольтке» — Moltke Крейсер «Мольтке» в Нью Йорке в 1912 году Основная информация Тип … Википедия

УГОЛ — муж. перелом, излом, колено, локоть, выступ или залом (впадина) об одной грани. Угол линейный, всякие две встречные черты и промежуток их; угол плоскостной или в плоскостях, встреча двух плоскостей или стен; угол толстый, теловой, встреча в одной … Толковый словарь Даля

Линейный крейсер «Гнейзенау» — Линкор … Википедия

ЛИНЕЙНЫЙ ОПЕРАТОР — А в векторном пространстве L отображение, сопоставляющее каждому вектору е век poro множества D (содержащегося в L и наз. областью определения Л. о.) др. вектор, обозначаемый Ае (и называемый значением Л. о. на векторе е). Выполнены след. условия … Физическая энциклопедия

Линейный корабль — У этого термина существуют и другие значения, см. Линейный корабль (значения). «Дредноут» родоначальник класса линкоров … Википедия

Линейный корабль Слава — Необходимо перенести содержимое этой статьи в статью «Слава (броненосец)». Вы можете помочь проекту, объединив статьи. В случае необходимости обсуждения целесообразности объединения, замените этот шаблон на шаблон <<к объединению>> … Википедия

Линейный крейсер «Фон-дер-Танн» — «Фон дер Танн» SMS Von der Tann Основная информация Тип Линейный крейсер … Википедия

Двугранный угол — и линейный угол двугранного угла … Википедия

Мольтке (линейный крейсер) — Линейный крейсер «Мольтке» Moltke … Википедия

Худ (линейный крейсер) — История Закладка киля: 1 сентября 1916 г. Спущен на воду: 22 а … Википедия

Источник

Скоро вебинар
«ПРЯМАЯ НА ПЛОСКОСТИ»
(Аналитическая геометрия). Жми подробнее.

Если в плоскости γ провести две пересекающиеся прямые АК и BN в точке М, то плоскость разделится ими на 4 области, которые образуют 4 «плоских » угла.

Аналогично две пересекающиеся плоскости γ и β по прямой АВ, делят пространство на 4 области и образуют 4 двугранных угла.

Определение. Двугранный угол – это фигура, образованная прямой АВ и двумя полуплоскостями с общей границей АВ, не принадлежащей одной плоскости.

Полуплоскости, образующие двугранный угол, называются гранями двугранного угла.

Общая для граней прямая АВ (граница полуплоскостей) называется ребром двугранного угла.

Обозначение: KABL, где K и L-это точки, лежащие в разных гранях, а АВ – ребро двугранного угла.

Измерение двугранных углов сводится к измерению линейных углов.
Определение. Линейным углом двугранного угла называется плоский угол, образованный двумя лучами, которые лежат в гранях этого двугранного угла и перпендикулярны его ребру.

Все линейные углы данного двугранного угла равны между собой.

За величину двугранного угла принимают величину его линейного угла.
Выражение двугранный угол равен ᵠ означает, что величина соответствующего линейного угла равна ᵠ.

Двугранный угол называется прямым (острым, тупым), если он равен 90°(меньше 90°, больше 90°)

Источник

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Понятие двугранного угла и угла между плоскостями

Напомним, что в планиметрии углом называют фигуру, состоящую из точки и двух лучей, выходящих из нее. Сама точка именуется вершиной угла, а лучи – сторонами угла.

По аналогии в стереометрии рассматривается схожая фигура – двугранный угол. Он состоит из двух полуплоскостей, которые исходят из одной прямой. Каждая из этих полуплоскостей именуется гранью двугранного угла, а их общая прямая – это ребро двугранного угла.

Для обозначения двугранного угла достаточно указать две точки на его ребре, а также ещё по одной точке на каждой грани. Например, на следующем рисунке показан угол САВD:

Двугранные углы часто встречаются в обычной жизни. Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.

Двугранные углы можно измерять. Для этого надо выбрать произвольную точку на ребре угла и на каждой грани построить перпендикуляр, проходящий через эту точку. Через эти два перпендикуляра можно построить единственную плоскость. Угол между двумя перпендикулярами и принимается за величину двугранного угла.

Отдельно отметим, что плоскость, проходящая через перпендикуляры (на рисунке выше это γ) перпендикулярна ребру угла АВ. Это вытекает из признака перпендикулярности прямой и плоскости. Действительно, АВ⊥ВС и АВ⊥BD, поэтому и АВ⊥γ. Построенный угол ∠СBD называют линейным углом двугранного угла.

Понятно, что в каждом двугранном угле можно построить сколько угодно линейных углов:

Здесь помимо ∠ВСD построены линейные углы ∠В’С’D’ и ∠В’’С’’D’’. Однако все эти углы имеют одинаковую градусную меру. Сравним, например, ∠ВСD и ∠В’С’D’. Так как BD⊥AB и B’D’⊥АВ, то BD||B’D’. Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.

Двугранные углы, как и обычные углы, можно разделить на острые (их градусная мера меньше 90°), прямые (они в точности равны 90°) и тупые (которые больше 90°).

Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла. Если среди них есть острый угол, то его величина считается углом между плоскостями. Если же все образуется 4 прямых двугранных угла, то угол между плоскостями принимается равным 90°.

Перпендикулярность плоскостей

В частном случае, когда угол составляет 90°, говорят, что пересекающиеся плоскости перпендикулярны.

Перпендикулярны друг другу пол и стены в доме, смежные грани кубика, стенки коробки. Существует особый признак перпендикулярности плоскостей.

Действительно, пусть плоскости α и β пересекаются по линии n, и в β есть такая прямая m, что m⊥α. Тогда m и n должны пересекаться в какой-нибудь точке К. Проведем в плоскости α через К прямую р, перпендикулярную n. Ясно, что m⊥р, ведь m⊥α. Получается, угол между m и р как раз и является углом между плоскостями α и β, ведь m⊥n и р⊥n. И этот угол равен 90°, ведь m⊥p, ч т. д.

Из доказанного признака вытекает следующее утверждение:

Прямоугольный параллелепипед

Ранее мы уже узнали про параллелепипед. Это фигура с 6 гранями, каждая из которых представляет собой параллелограмм. Особый интерес представляет его частный случай – прямоугольный параллелепипед.

Такую форму имеют многие шкафы, другие предметы мебели, коробки для обуви, небоскребы. Изображают прямоугольный параллелепипед так:

Для обозначения вершин параллелепипеда применяют латинские буквы. Очень часто для вершин одной грани используют 4 буквы без индекса (на рисунке выше это А, В, С, D), а другие 4 вершины обозначают такими же буквами, но с нижним индексом 1: А₁, B₁, C₁ и D₁. При этом одноименные вершины (например, А и А₁) находятся на одном ребре, которое располагается на рисунке вертикально.

Докажем некоторые свойства прямоугольного параллелепипеда.

Например, ребро АD пересекается с гранями АВВ₁А₁ и CDD₁C₁. Значит, оно перпендикулярно этим граням (точнее говоря, оно перпендикулярно плоскостям, проходящим через эти грани). Действительно, AD⊥DC, ведь ∠ADC является углом в прямоугольнике АВСD и потому он прямой. Аналогично и AD⊥DD₁, ведь и ADD₁A₁ – прямоугольник. Получается, что ребро AD перпендикулярно 2 прямым в грани CDD₁C₁ (которые при этом пересекаются), и потому оно перпендикулярно и всей грани. То же самое можно продемонстрировать для любого ребра прямоугольного параллелепипеда и любой грани, которую она пересекает.

Эти грани пересекаются по ребру А₁D₁. Этому ребру в свою очередь перпендикулярны ребра АА₁ и А₁В₁, лежащие в гранях ADD₁A₁ и A₁D₁C₁B₁. Значит, ∠АА₁В₁ и будет углом между этими гранями. Но он составляет 90°, то есть грани перпендикулярны, ч. т. д.

Хотя у прямоугольного параллелепипеда есть 12 граней, многие из них имеют одинаковую длину. Поэтому для описания размеров этой фигуры достаточно указать только три параметра. Обычно их называют длиной, шириной и высотой:

Эти параметры также называют измерениями прямоугольного параллелепипеда. Зная их, можно вычислить длину диагонали прямоугольного параллелепипеда. Для этого используется следующая теорема:

Действительно, пусть есть прямоугольный параллелепипед АВСDA₁B₁C₁D₁. Назовем ребро AD его длиной, АВ – шириной, а ВВ₁ – высотой. Пусть необходимо найти длину диагонали В₁D:

Сначала построим отрезок BD и рассмотрим ∆ABD. Он прямоугольный, и потому для него верна теорема Пифагора:

Теперь перейдем к ∆В₁ВD. Так как ребро BB₁ перпендикулярно грани ABCD, то ∠В₁ВD – прямой. Тогда и ∆В₁ВD – прямоугольный, а потому и для него можно записать теорему Пифагора:

Дополнительно отметим уже известный нам факт, что тот прямоугольный параллелепипед, у которого все стороны одинаковы, именуется кубом. Можно дать и такое определение куба:

Трехгранный угол

Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости:

В результате мы получили фигуру, которую именуют трехгранным углом. Она состоит их трех плоских углов: ∠АКС, ∠АКВ и ∠ВКС. Эти углы так и называются – плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС. Обратите внимание, что через каждую пару лучей КА, КВ и КС можно провести плоскость. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани. Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла:

Доказательство. Пусть в пространстве из точки D выходят лучи AD, BD и CD. Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется. Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:

Это возможно сделать, ведь ∠BDC > AD, поэтому внутри ∠BDC можно провести луч DK. Далее «сместим» точку А на луче АD так, чтобы DK = AD. Естественно, что при этом плоские углы трехгранного угла никак не изменятся, также как останется верным равенство

Сравним ∆ADC и ∆DKC. У них есть общая сторона DC, одинаковы стороны DK и AD, а также совпадают углы между ними. Значит, эти треугольники равны, и тогда можно записать, что:

Теперь сравним ∆ABD и ∆DBK. У них BD – общая сторона, а DK = AD. При этом BK 1 параллельны друг другу

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №11. Перпендикулярность плоскостей

Перечень вопросов, рассматриваемых в теме.

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Перпендикуляры к ребру двугранного угла образуют линейный угол двугранного угла. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Если угол между пересекающимися плоскостями равен 90 градусом, то плоскости перпендикулярны.

Признак перпендикулярности плоскостей: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Следствие из признака перпендикулярности плоскостей: Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

Прямоугольный параллелепипед – фигура, у которой все боковые ребра перпендикулярны основанию.

Атанасян Л.С., Бутузов В.Ф. Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.

Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. Прямая а, которая является общей границей полуплоскостей, называется ребром двугранного угла (рис. 1а и 1б).

Двугранный угол с ребром CD, на разных гранях которого отмечены точки A и B называют двугранным углом CABD.

Перпендикуляры к ребру AO и BO образуют линейный угол двугранного угла AOB (рис. 1в). Так как луч ОА перпендикулярен прямой CD и луч OB перпендикулярен прямой CD, то плоскость АОВ перпендикулярна к прямой CD. Таким образом, плоскость линейного угла перпендикулярна к ребру двугранного угла. Двугранный угол имеет бесконечное множество линейных углов

Градусной мерой двугранного угла называется градусная мера его линейного угла. Так же как и плоские углы, двугранные углы могут быть прямыми, острыми и тупыми.

Все линейные углы двугранного угла равны друг другу.

Рассмотрим два линейных угла АОВ и А₁О₁В₁ (рис. 1г). Лучи ОА и О₁А₁, лежат в одной грани и перпендикулярны к прямой ОО₁, поэтому они сонаправлены. Точно так же сонаправлены лучи OB и O₁B₁. Поэтому углы АОВ и А₁О₁В₁ равны как углы с сонаправленными сторонами.

Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.

Если один из этих двугранных углов равен фи, то другие три угла равны соответственно 180 градусов минус фи, фи и 180 градусов минус фи (рис. 2 а). В частности, если один из углов прямой, то и остальные три угла прямые. Если угол между пересекающимися плоскостями равен 90 градусом, будем называть такие плоскости перпендикулярными (рис. 2б).

Для доказательства теоремы рассмотрим плоскости альфа и бетта такие (рис. 3), что плоскость альфа проходит через прямую АВ, перпендикулярную к плоскости бетта и пересекающуюся с ней в точке А. Докажем, что плоскости альфа и бетта перпендикулярны. Плоскости альфа и бетта пересекаются по некоторой прямой АС. При этом прямая АВ перпендикулярна прямой АС, так как по условию прямая АВ перпендикулярна плоскости бетта, это означает, что прямая АВ перпендикулярна к любой прямой, лежащей в плоскости бетта.

Проведем в плоскости бетта прямую AD, перпендикулярную к прямой АС. Тогда угол BAD — линейный угол двугранного угла, образованного при пересечении плоскостей альфа и бетта. Но угол BAD равен 90 градусов так как прямая АВ перпендикулярна плоскости бетта. Следовательно, угол между плоскостями альфа и бетта равен 90 градусов. Что и требовалось доказать.

Из этой теоремы вытекает важное следствие:

Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

На рисунке 4 представлен прямоугольный параллелепипед. У этой фигуры все боковые ребра перпендикулярны основанию.

Его основаниями служат прямоугольники ABCD и A₁B₁C₁D₁, а боковые ребра АА₁,BB₁,CC₁ и DD₁ перпендикулярны к основаниям. Отсюда следует, что ребро АА₁ перпендикулярно к ребру АВ, т. е. боковая грань АА₁В₁В является прямоугольником. То же самое можно сказать и об остальных боковых гранях.

Таким образом, прямоугольный параллелепипед обладает следующими свойствами:

1) В прямоугольном параллелепипеде все шесть граней — прямоугольники.

2) Все двугранные углы прямоугольного параллелепипеда — прямые.

3) Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Измерениями прямоугольного параллелепипеда называются длины трех ребер, имеющих общую вершину.

Докажем последнее свойство.

Так как ребро СС₁ перпендикулярно к основанию ABCD, то угол АСС₁, прямой. Из прямоугольного треугольника АСС₁, по теореме Пифагора получаем

Следствием из этого свойства является то, что диагонали прямоугольного параллелепипеда равны.

Стоит отметить, что если у прямоугольного параллелепипеда все три измерения равны, то он называется, а все его грани являются равными друг другу квадратами.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ (рис. 5) боковая грань DD₁C₁C – квадрат, DC равно 4 см, BD₁ равно 6 см. Найдите BC и докажите, что плоскости BCD₁ и DC₁ B₁ взаимно перпендикулярны.

Сначала найдем BC. Воспользуемся тем свойством прямоугольного параллелепипеда, что квадрат его диагонали равен сумме квадратов трех его измерений.

Тогда диагональ BD₁ в квадрате равна AD в квадрате плюс DD₁ в квадрате плюс DC в квадрате. BD₁ – известно из условия, DD₁ и DC – стороны квадрата и тоже известны из условия, тогда отсюда мы можем выразить ребро AD, которое ребру BC.Отсюда находим, что BC равно 2 сантиметрам.

Для доказательства перпендикулярности плоскостей BCD₁ и DC₁ B₁ воспользуемся признаком перпендикулярности плоскостей. Этот признак звучит следующим образом: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Заметим, что плоскость BCD₁ проходит через диагональ грани DD₁ C₁C – CD₁. Эта диагональ перпендикулярна плоскости DC₁ B₁ в соответствии с признаком перпендикулярности прямой и плоскости, так как CD₁ перпендикулярна второй диагонали квадрата – C₁D и перпендикулярна ребру прямоугольного параллелепипеда C₁ B₁. Что и требовалось доказать.

Тестовый вопрос №2. В прямом двугранном угле дана точка A. Расстояния от точки A до граней угла: AA₁=6 см и AB₁=8 см. Определите расстояние от точки A до ребра двухгранного угла.

Отрезки AA₁ и AB₁ перпендикулярны граням двугранного угла, поэтому AA₁BB₁ – прямоугольник. Искомое расстояние – диагональ этого прямоугольника, которую найдем с помощью теоремы Пифагора: сантиметров.

Тестовый вопрос №10. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ длины рёбер: AB = 2, BC=3, AA₁ = 4. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C_​1​​.

Решение. Нарисуем рисунок.

В рассматриваемом прямоугольном параллелепипеде проведем отрезок BC_​1​​. Затем построим плоскость на прямых BC_​1​​ и AB. Так как плоскости прямоугольного параллелепипеда AA₁D₁D и BB₁C₁C параллельны, поэтому искомым сечением является прямоугольник ABC₁D₁.

Источник

Двугранные углы

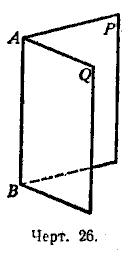
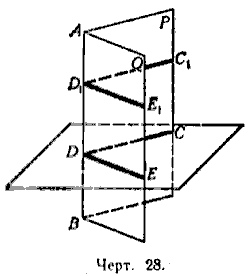
Если из произвольной точки D ребра AB (черт. 28) проведём на каждой грани по перпендикуляру к ребру, то образованный ими угол CDE называется линейным углом двугранного угла.

Величина линейного угла не зависит от положения его вершины на ребре. Так, линейные углы CDE и C₁D₁E₁ равны, потому что их стороны соответственно параллельны и одинаково направлены.

Плоскость линейного угла перпендикулярна к ребру, так как она содержит две прямые, перпендикулярные к нему. Поэтому для получения линейного угла достаточно грани данного двугранного угла пересечь плоскостью, перпендикулярной к ребру, и рассмотреть получившийся в этой плоскости угол.

Равенство и неравенство двугранных углов

Два двугранных угла считаются равными, если они при вложении могут совместиться; в противном случае тот из двугранных углов считается меньшим, который составит часть другого угла.

Подобно углам в планиметрии, двугранные углы могут быть смежные, вертикальные и пр.

Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.

1) Равным двугранным углам соответствуют равные линейные углы.

2) Большему двугранному углу соответствует больший линейный угол.

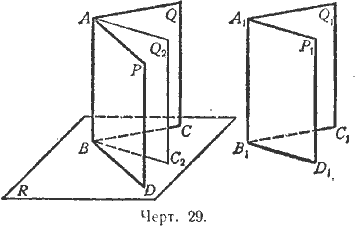
Тогда если эти двугранные углы равны, то грань Q₁ совпадёт с гранью Q; если же угол А₁В₁ меньше угла AB, то грань Q₁ займёт некоторое положение внутри двугранного угла, например Q₂.

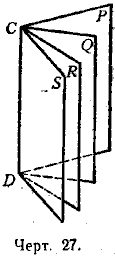
Заметив это, возьмём на общем ребре какую-нибудь точку В и проведём через неё плоскость R, перпендикулярную к ребру. От пересечения этой плоскости с гранями двугранных углов получатся линейные углы. Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол CBD; если же двугранные углы не совпадут, если, например, грань Q₁ займёт положение Q₂, то у большего двугранного угла окажется больший линейный угол (именно: ∠CBD > ∠C₂BD).

1) Равным линейным углам соответствуют равные двугранные углы.

2) Большему линейному углу соответствует больший двугранный угол.

Эти теоремы легко доказываются от противного.

1) Прямому двугранному углу соответствует прямой линейный угол, и обратно.

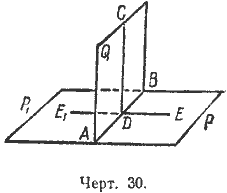
Пусть (черт. 30) двугранный угол PABQ прямой. Это значит, что он равен смежному углу QABP₁. Но в таком случае линейные углы CDE и CDE₁ также равны; а так как они смежные, то каждый из них должен быть прямой. Обратно, если равны смежные линейные углы CDE и CDE₁, то равны и смежные двугранные углы, т.е. каждый из ни должен быть прямой.

2) Bcе прямые двугранные углы равны, потому что у них равны линейные углы.

Подобным же образом легко доказать, что:

3) Вертикальные двугранные углы равны.

4) Двугранные углы с соответственно параллельными и одинаково (или противоположно) направленными гранями равны.

5) Если за единицу двугранных углов возьмём такой двугранный угол, который соответствует единице линейных углов, то можно сказать, чтo двугранный угол измеряется его линейным углом.

Источник