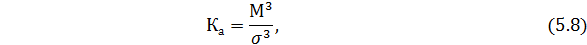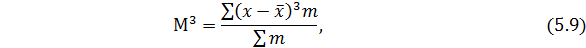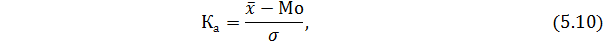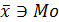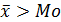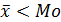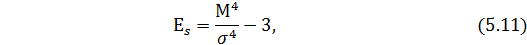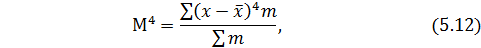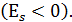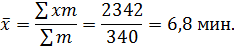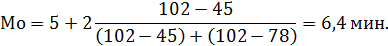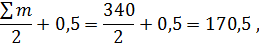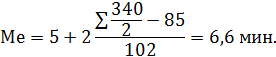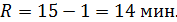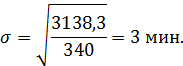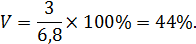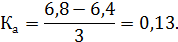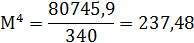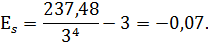Что такое коэффициент асимметрии

Показатели асимметрии

Асимметрия и эксцессявляютсяхарактеристиками формы распределения.

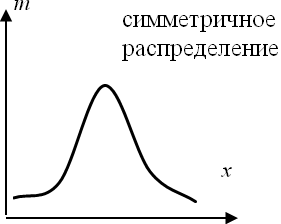
В практике статистического исследования приходится встречаться с различными распределениями. Идеальным (нормальным) распределением является такое, у которого распределение признака в совокупности симметричное, при этом мода и средняя совпадают.

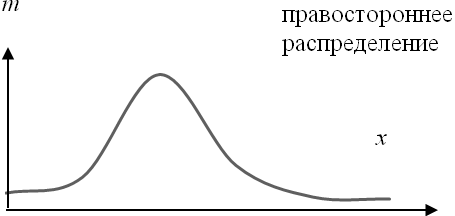
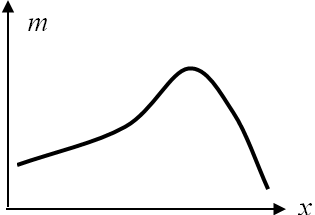
Однако чаще всего встречается асимметрическое распределение. При правосторонней асимметрии, средняя арифметическая больше моды, а при левосторонней, наоборот.

Для оценки степени асимметричности применяют моментный и структурный коэффициент асимметрии.

Моментный коэффициент асимметрии определяется по формуле:

где 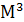— центральный момент третьего порядка. Определяется по

Структурные показатели асимметрии характеризуют асимметричность только в центральной части распределения, т.е. основной массы единиц.

Наиболее часто применяют структурный коэффициент асимметрии, который определяется по формуле:

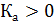
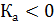
Если , асимметрия правосторонняя, если , асимметрия левосторонняя.

Формы распределения признаков в совокупности приведены на рис. 5.4.

Рис. 5.4. Формы распределения признаков в совокупности

Другим свойством рядов распределения является эксцесс. Под эксцессом понимают островершинность или плосковершиннсоть распределения по сравнению с нормальным распределением, т. е. эксцесс – это отклонение вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.

Эксцесс оценивается с помощью показателя, представлено формулой:

где 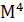— центральный момент 4-го порядка, который определяется по

Распределение островершинное обладает положительным эксцессом ( , а плосковершинное – отрицательным эксцессом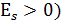

На рис. 5.5 представлено нормальное, островершинное и плосковершинное распределение.

1 – нормальное распределение

2 – островершинное распределение

3 – плосковершинное распределение

Рис. 5.5. Формы распределения вариационного ряда

Пример 2.Для определения средней продолжительности представленных междугородних разговоров проведено выборочное наблюдение, в выборку попало 340 разговоров. Распределение этих разговоров по продолжительности представлено в виде вариационного ряда в таблице 5.1. Определить основные характеристики вариационного ряда. Ряд изобразить графически в виде гистограммы.

Группа телефон-ных разговоров по продол- житель-ности (мин.)	Коли- чество разгово- ров m	Середина интервала x	xm	Накоплен- ные частоты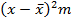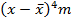
До 3 3-5 5-7 7-9 9-11 11-13 Более 13	921,6 352,8 65,28 112,3 419,8 540,8 725,7	212,33 41,8 161,7
Итого	80745,9

1. Определяется средняя продолжительность междугородних разговоров:

2. Рассчитывается мода, при этом модальный интервал 5-7:

Это означает, что большинство разговоров имеет продолжительность 6,4 мин.

3. Определяется медиана, для этого определяются накопленные частоты.

Сначала находится следующее соотношение:

Сравнивая его с накопленными частотами, можно сказать, медиальный интервал будет равен 5-7 мин.

Таким образом, половина разговоров имеет продолжительность до 6,6 мин., а половина больше.

4. Размах колебаний будет равен:

при этом первый и последний интервал закрываются.

5. Среднее квадратическое отклонение составит:

6. Коэффициент вариации:

В среднем продолжительность каждого разговора отклоняется от среднего значения на 3 мин. или на 44%. Совокупность не однородная, так как 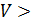33%, а средняя не типична для данной совокупности.

7. Коэффициент асимметрии:

Так как 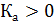, это означает, что распределения имеют форму правосторонней асимметрии.

Рассчитывается эксцесс, но сначала определяется момент 4-го порядка:

9. Эксцесс будет равен:

Это означает, что распределение плосковершинное. Графическое изображение ряда представлено на рис. 5.6.

Рис. 5.6. Гистограмма распределения телефонных разговоров по продолжительности

Источник

Тема 6 Показатели вариации

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явления. Необходимо учитывать и разброс или вариацию значений отдельных единиц.

Основными показателями, характеризующими вариацию, являются: размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Размах вариации – простейший показатель, разность между максимальным и минимальным значениями признака.

\[ \begin R=x_-x_ \end \] Недостатком является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.

Дисперсия – средний квадрат отклонений значений признака от их средней величины и определяется по формулам простой

Если коэффициент вариации не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.

Показатели вариации могут быть использованы не только в анализе изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е.е в анализе взаимосвязей между показателями.

При проведении такого анализа совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным и результативным.

Для выявления взаимосвязи исходная совокупность делится на две или более групп по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:

Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней:

Если факторный признак, по которому производится группировка, не оказывает никакого влияния на результативный признак, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая средняя будет равна нулю.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:

Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

\[ \begin \eta_э = \sqrt < \frac <\delta^2> <\sigma_o^2>> \end \] Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

Среди множества варьирующих признаков, изучаемых статистикой, существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Альтернативный признак принимает всего два значения – 0 и 1 с весами соответственно p и q. Поэтому среднее значение альтернативного признака равно р. А дисперсия альтернативного признака равна pq. Дисперсия альтернативного признака равна произведению доли признака, обладающего характеристикой на долю признака, не обладающего характеристикой. Предельное значение дисперсии для альтернативного признака равно 0,25 при р=0,5.

Дисперсия альтернативного признака широко применяется в выборочном обследовании.

Изменения частот в вариационных рядах изменяются закономерно в связи с изменением варьирующего признака. Такие закономерности называются закономерностями распределения.

Основная задача анализа вариационных рядов заключается в выявлении подлинной закономерности распределения путем исключения влияния второстепенных, случайных для данного распределения факторов.

Если увеличить объем совокупности и уменьшить интервал в группах, то графическое изображение приближается к некоторой плавной кривой, которая называется кривой распределения.

Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.

Теоретическая кривая распределения – кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для него факторов.

Выяснение общего характера распределения предполагает оценку его однородности, а также расчет показателей асимметрии и эксцесса.

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии:

Его величина может быть положительной (для правосторонней асимметрии) и отрицательной (для левосторонней асимметрии).

Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной. Если асимметрия меньше 0,25, она считается незначительной.

Если коэффициент асимметрии находится в интервале от 0,25 до 0,5, то наличие асимметрии в генеральной совокупности проверяется с помощью определения оценки существенности на основе средней квадратической ошибки:

Для симметричных распределений может быть рассчитан показатель эксцесса, который показывает, насколько резкий скачок имеет изучаемое явление. Показатель эксцесса определяется на основе центрального момента четвертого порядка по формуле:

Если показатель эксцесса больше нуля, то распределение островершинное и скачок считается значительным, если коэффициент эксцесса меньше нуля, то распределение считается плосковершинным и скачок считается незначительным. Среднеквадратическая ошибка эксцесса показывает, насколько существенен скачок в явлении и рассчитывается по формуле:

\[ \begin \sigma_ = \sqrt < \frac<24n(n-2)(n-3)> <(n-1)^2(n+3)(n+5)>> \end \] К структурным характеристикам ряда распределения относятся мода, медиана, квартили, децили и перцентили.

Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль первого порядка (нижний квартиль) и квартиль третьего порядка (верхний квартиль). Каждый из них отсекает соответственно ¼ и ¾ совокупности. Для расчета квартилей используются следующие формулы:

Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль отсекает 1/10 часть совокупности, а девятый дециль отсекает 9/10 частей. Рассчитываются децили по аналогичным формулам:

Перцентили – варианты, которые делят ранжированную совокупность на 100 частей.

Источник

Понятие параметрических тестов, ассиметрии и эксцесса

В данной статье представлены важные категории логически выводимых статистических тестов и обсуждаются параметры описательной статистики, относящиеся к нормальному распределению.

Добро пожаловать в нашу серию статей о статистике в электротехнике. Ранее мы рассмотрели статистический анализ и описательный анализ в электротехнике, а затем обсудили среднее отклонение, стандартное отклонение и дисперсию в обработке сигналов.

Теперь мы перешли к исследованию нормального распределения в электротехнике, в частности, как понимать гистограммы, вероятность и кумулятивную функцию распределения нормально распределенных данных. Данная статья расширяет это обсуждение, касаясь параметрических тестов, асимметрии и эксцесса.

Когда нормальное распределение не выглядит нормальным

В предыдущих статьях мы рассмотрели нормальное распределение (также известное как распределение Гаусса) как идеализированное математическое распределение и как гистограмму, полученную из эмпирических данных. Если измеряемое явление характеризуется нормальным распределением значений, форма гистограммы по мере увеличения размера выборки будет всё больше похожа на колоколообразную (гауссову) кривую.

Однако это приводит нас к интересному вопросу: как мы узнаем, что явление характеризуется нормальным распределением значений?

Если у нас есть большой объем данных, мы можем просто посмотреть на гистограмму и сравнить ее с гауссовой кривой. Однако с меньшими наборами данных ситуация будет сложнее. Даже если мы анализируем базовый процесс, который действительно создает нормально распределенные данные, гистограммы, созданные из небольших наборов данных, могут оставлять место для сомнений.

Рисунок 1 – Распределены ли эти данные нормально?

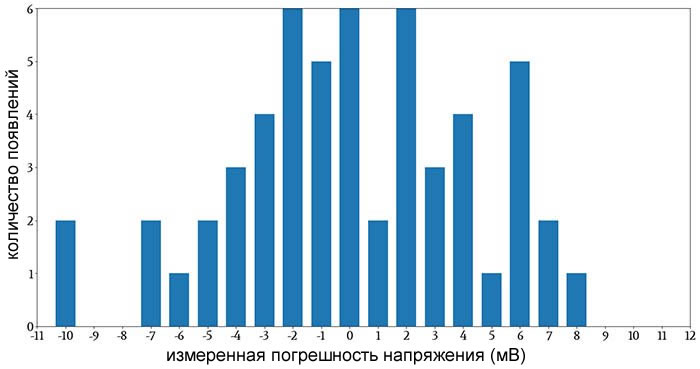
В данной статье мы обсудим два описательных статистических показателя (асимметрию и эксцесс), которые помогут нам определить, соответствуют ли наши данные нормальному распределению.

Однако сначала я хочу изучить связанный с этим вопрос: почему нас волнует, соответствует ли набор данных нормальному распределению?

Параметрические и непараметрические тесты

Существуют различные статистические методы, помогающие нам анализировать и интерпретировать данные, и некоторые из этих методов относятся к категории статистических выводов. Мы часто используем слово «тест», когда говорим о статистической процедуре вывода, и эти тесты могут быть параметрическими или непараметрическими.

Различие между параметрическими и непараметрическими тестами заключается в характере данных, к которым применяется тест. Когда набор данных демонстрирует распределение, которое в достаточной степени согласуется с нормальным распределением, можно использовать параметрические тесты. Когда данные не распределены нормально, мы переходим к непараметрическим тестам.

Примерами параметрических тестов являются парный t-критерий, односторонний дисперсионный анализ (ANOVA) и коэффициент корреляции Пирсона. Непараметрическими альтернативами этим критериям являются, соответственно, критерий знаковых рангов Уилкоксона, критерий Краскела–Уоллиса и ранговая корреляция Спирмена.

Почему «параметрический» и «непараметрический»?

Если вас смущает эта терминология параметрический/непараметрический, вот объяснение: параметр – это характеристика всей генеральной совокупности (совокупности значений), например, средний рост всех канадцев или стандартное отклонение выходных напряжений, генерируемых всеми микросхемами эталонного напряжения REF100 (я придумал эту модель микросхемы).

Обычно мы не можем знать параметр с уверенностью потому, что наши данные представляют собой только выборку из генеральной совокупности. Однако мы можем произвести оценку параметра, вычислив соответствующее статистическое значение на основе выборки.

Параметрические тесты основываются на предположениях, связанных с нормальностью распределения генеральной совокупности, и параметрами, которые характеризуют это распределение. Когда данные не распределены нормально, мы не можем делать такие предположения, и, следовательно, мы должны использовать непараметрические тесты.

Зачем заморачиваться с параметрическими тестами?

Если существуют непараметрические тесты и их можно применять независимо от нормальности распределения, зачем утруждать себя определением, является ли распределение нормальным? Давайте, просто применим непараметрический тест и покончим с этим!

Есть простая причина, по которой мы избегаем непараметрических тестов, когда данные достаточно нормальны: параметрические тесты, как правило, более эффективны. «Эффективность» в статистическом смысле означает, насколько эффективно тест обнаружит взаимосвязь между переменными (если эта взаимосвязь существует). Мы можем сделать любой тип тестов более эффективным, увеличив размер выборки, но для того, чтобы получить наилучшую информацию из имеющихся данных, мы по возможности используем параметрические тесты.

Оценка нормальности: асимметрия и эксцесс

Мы можем попытаться определить, демонстрируют ли эмпирические данные неопределенно нормальное распределение, просто взглянув на гистограмму. Однако, чтобы решить, является ли распределение достаточно нормальным, чтобы оправдать использование параметрических тестов, нам могут потребоваться дополнительные аналитические методы.

Асимметрия

Один из этих методов – вычислить асимметрию набора данных. Нормальное распределение идеально симметрично относительно среднего, и, таким образом, любое отклонение от идеальной симметрии указывает на некоторую степень ненормальности измеренного распределения.

На следующем рисунке представлены примеры асимметричных форм распределения.

Рисунок 2 – Изображение положительной асимметрии, нулевой асимметрии и отрицательной асимметрии

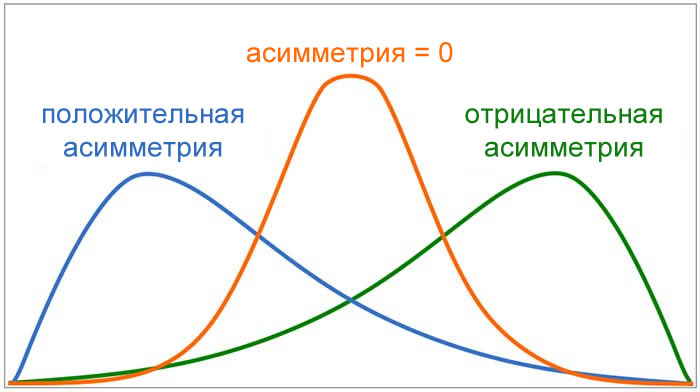
Асимметрия может представляться положительным или отрицательным числом (или нулем). Распределения, симметричные относительно среднего значения, такие как нормальное распределение, имеют нулевую асимметрию. Распределение, которое «наклоняется» вправо, имеет отрицательную асимметрию, а распределение, которое «наклоняется» влево, имеет положительную асимметрию.

Как правило, значения асимметрии, которые находятся в пределах ±1 от асимметрии нормального распределения, указывают на достаточную нормальность для использования параметрических тестов.

Эксцесс

Мы используем эксцесс, чтобы количественно оценить тенденцию явления создавать значения, далекие от среднего. Существуют различные способы описания информации, которую эксцесс передает о наборе данных: «хвостатость» (обратите внимание, что значения, далекие от среднего, находятся в хвостах распределения), «величина хвоста» или «вес хвоста» и «островершинность» (последнее несколько проблематично, потому что эксцесс напрямую не измеряет остроту или гладкость).

Нормальное распределение имеет значение эксцесса 3. Следующая диаграмма дает общее представление о том, как эксцесс больше или меньше 3 соответствует формам ненормального распределения.

Рисунок 3 – Обратите внимание, что эксцесс больше или меньше 3 соответствует формам, отличным от нормального распределения.

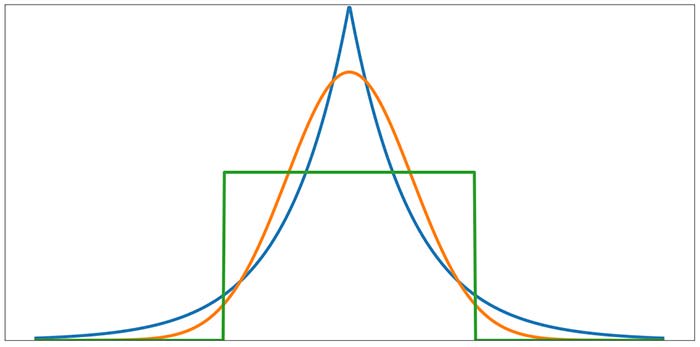
Оранжевая кривая – нормальное распределение. Обратите внимание, что синяя кривая по сравнению с оранжевой кривой имеет большую «величину хвоста», то есть большую массу вероятности в хвостах. Эксцесс синей кривой, которая называется распределением Лапласа, равен 6. Зеленая кривая называется равномерным распределением; вы можете видеть, что хвосты отсутствуют. Эксцесс равномерного распределения равен 1,8.

Как и в случае асимметрии, общее правило состоит в том, что эксцесс в пределах ±1 от эксцесса нормального распределения указывает на достаточную нормальность.

Заключение

Конечно, о параметрических тестах, асимметрии и эксцессе можно сказать гораздо больше, но я думаю, что мы рассмотрели достаточно материала для вводной статьи. Обобщим вышесказанное:

Источник

Коэффициент асимметрии

Коэффицие́нт асимметри́и в теории вероятностей — величина, характеризующая асимметрию распределения данной случайной величины.

Определение

Пусть задана случайная величина , такая что . Пусть обозначает третий центральный момент: , а — стандартное отклонение . Тогда коэффициент асимметрии задаётся формулой:

.

Замечания

См. также

Полезное

Смотреть что такое «Коэффициент асимметрии» в других словарях:

КОЭФФИЦИЕНТ АСИММЕТРИИ — 1. В литологии коэф., применяемый при обработке данных гранулометрических анализов, позволяющий судить, на какую относительную величину и в какую сторону (больших или меньших размеров) сдвинута мода (диаметр, наиболее распространенных частиц)… … Геологическая энциклопедия

коэффициент асимметрии — — [В.А.Семенов. Англо русский словарь по релейной защите] Тематики релейная защита EN asymmetry coefficient … Справочник технического переводчика

коэффициент асимметрии — 3.1.4 коэффициент асимметрии: Отношение напряжения (или тока) однотактной (несимметричной) волны к напряжению (или току) двухтактной (симметричной) волны. Источник … Словарь-справочник терминов нормативно-технической документации

коэффициент асимметрии — asimetrijos koeficientas statusas T sritis radioelektronika atitikmenys: angl. asymmetry coefficient vok. Unsymmetriefaktor, m rus. коэффициент асимметрии, m pranc. coefficient d asymétrie, m … Radioelektronikos terminų žodynas

коэффициент асимметрии тока варистора — Отношение разности проходящих через варистор токов при изменении полярности прикладываемого напряжения к наименьшему значению одного из этих токов. [ГОСТ 21414 75] Тематики резисторы … Справочник технического переводчика

коэффициент асимметрии цикла — Величина, характеризующая влияние на сопротивление усталости материала неравного отклонения переменных напряжений от их среднего значения. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом … Справочник технического переводчика

коэффициент асимметрии цикла нагружения — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN load ratio … Справочник технического переводчика

коэффициент асимметрии цикла напряжений — ρб Отношение минимального напряжения к максимальному. [ГОСТ 24545 81] Тематики бетон … Справочник технического переводчика

Коэффициент асимметрии цикла напряжений — rб Отношение минимального напряжения к максимальному Источник: ГОСТ 24545 81: Бетоны. Методы испытаний на выносливость оригинал документа … Словарь-справочник терминов нормативно-технической документации

Коэффициент асимметрии цикла напряжений — – отношение минимального напряжения к максимальному. [ГОСТ 24545 81] Рубрика термина: Испытания бетона Рубрики энциклопедии: Абразивное оборудование, Абразивы, Автодороги … Энциклопедия терминов, определений и пояснений строительных материалов

Источник