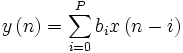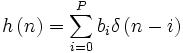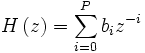Что такое ких фильтр
КИХ-фильтр
Фильтр с конечной импульсной характеристикой (нерекурсивный фильтр, КИХ-фильтр, FIR-фильтр) — один из видов линейных электронных фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Такой фильтр называют ещё нерекурсивным из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра — некая константа.
Содержание
Динамические характеристики
Для того, чтобы найти ядро фильтра положим
где δ(n) — дельта-функция. Тогда импульсная характеристика КИХ-фильтра может быть записана как:
Z-преобразование импульсной характеристики даёт нам передаточную функцию КИХ-фильтра:
Свойства
КИХ-фильтр обладает рядом полезных свойств, из-за которых он иногда более предпочтителен в использовании, чем БИХ-фильтр. Вот некоторые из них:
См. также
Ссылки
Полезное
Смотреть что такое «КИХ-фильтр» в других словарях:
Фильтр с конечной импульсной характеристикой — (Нерекурсивный фильтр, КИХ фильтр) или FIR фильтр (FIR сокр. от finite impulse response конечная импульсная характеристика) один из видов линейных цифровых фильтров, характерной особенностью которого является ограниченность по времени … Википедия
Фильтр Бесселя — Линейные электронные фильтры Фильтр Баттерворта Фильтр Чебышева Эллиптический фильтр Фильтр Бесселя Фильтр Гаусса Фильтр Лежандра Фильтр Габора … Википедия
Фильтр с бесконечной импульсной характеристикой — (Рекурсивный фильтр, БИХ фильтр) или IIR фильтр (IIR сокр. от infinite impulse response бесконечная импульсная характеристика) линейный электронный фильтр, использующий один или более своих выходов в качестве входа, то есть… … Википедия
Нерекурсивный фильтр — Фильтр с конечной импульсной характеристикой (нерекурсивный фильтр, КИХ фильтр, FIR фильтр) один из видов линейных электронных фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого … Википедия
Цифровой фильтр — Цифровой фильтр в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового, аналоговый фильтр имеет дело с аналоговым сигналом, его свойства… … Википедия
Дискретный фильтр — Цифровой фильтр в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны,… … Википедия
Рекурсивный фильтр — Фильтр с бесконечной импульсной характеристикой (Рекурсивный фильтр, БИХ фильтр) линейный электронный фильтр, использующий один или более своих выходов в качестве входа, то есть образует обратную связь. Основным свойством таких фильтров является … Википедия
Линейный фильтр — Линейный фильтр динамическая система, применяющая некий линейный оператор ко входному сигналу для выделения или подавления определённых частот сигнала и других функций по обработке входного сигнала. Линейные фильтры широко применяются в… … Википедия
Скользящая средняя (фильтр) — У этого термина существуют и другие значения, см. Скользящая средняя (значения). Блок схема простого КИХ фильтра второго порядка, реализующего скользящее среднее Скользящая средняя, скользящее среднее разновидность цифрового фильтра с… … Википедия
Медианный фильтр — Пример использования медианного фильтра к зашумленному изображению с 3 различными значениями радиуса окна фильтрации. Обработка изображения выполнена в Adobe Photoshop. Медианны … Википедия
Построение цифрового фильтра с конечной импульсной характеристикой
Вступление издалека
Недавно передо мной встала достаточно интересная задача, с которой я раньше никогда не сталкивался — борьба с шумом. Мы принимали сигнал с датчиков на аналогово-цифровой преобразователь (АЦП)
А так как данная тема для меня была (хотя и сейчас есть кое-где) темным лесом, я пошел мучить вопросами гугл, мне показалось освещена эта тема не очень подробно и доступно, поэтому решил написать статью с примером разработки и готовым исходником.
Ближе к делу
Цифровые фильтры могут быть двух видов – с конечной и с бесконечной импульсной характеристикой (КИХ и БИХ). Для решения моей задачи подходит КИХ-фильтр, поэтому про него и расскажу.
Для начала посмотрим как же он работает:
Здесь показан пример фильтра нижних частот, как видно на рисунке, этот фильтр пропускает нижние частоты, а все остальные старается отсечь (подавление), или хотя бы ослабить (переход). Отклонения в полосе пропускания и полосе подавления выбираются в зависимости от принимаемого сигнала, но при использовании различных весовых функций, на них могут накладываться определенные ограничения. Например, если используется весовая функция Хэмминга, то эти отклонения будут равны между собой.
Ширина полосы перехода ∆F зависит от длины фильтра и от весовой функции (для функции Блэкмена ∆F=5,5|N).
Работает фильтр довольно просто: фильтр получает значения, с помощью коэффициентов преобразует их и выдаёт выходную последовательность, тогда с формулой самого фильтра всё понятно:
Она реализуется через цикл, но постойте, а где же взять нужные коэффициенты? Вот тут-то как раз и зарыта собака (и не одна).
Параметры фильтра
Естественно для разных фильтров нужны разные коэффициенты, и для этого нужно определиться с параметрами фильтра, это обычно сначала делается теоретически (с умным видом прикидываем какая у нашего сигнала частота, потом частоты, которые надо отсеивать), а потом изучаем АЧХ реальных измерений (и осознаем, как сильно мы ошибались).
По этим АЧХ мы определяемся с идеальной частотной характеристикой (какие частоты проходят свободно, какие мы убираем и как сильно), теперь нам нужна идеальная импульсная характеристика её можно посчитать как Фурье-образ от идеальной частотной:
где H_D(w) – идеальная характеристика.
Но можно пойти и по более простому пути – есть уже заранее вычисленные идеальные импульсные характеристики, например для фильтра нижних частот формула выглядит следующим образом:

где fc и wc – частота среза.
Итак, осталось уже немного идеал идеалом, а мы имеем дело с практикой, и нам нужна «реальная» импульсная характеристика. Для её расчета нам понадобится весовая функция w(n), их есть несколько разновидностей, в зависимости от требований к фильтру (Хэмминга, Хеннинга, Блэкмена, Кайзера, о них не говорю, ибо статья и так большая), в нашем случае я использую функцию Блэкмена:
где N – длина фильтра, т.е. количество коэффициентов.
Теперь надо перемножить идеальную импульсную характеристику и весовую функцию:
Финишная прямая
Теперь мы готовы рассчитать выходные значения, по формуле фильтра, она самая первая в этой статье, ну вот и всё, в завершение привожу исходный код фильтра:
КИХ фильтр на Verilog
Однако, есть нюансы.
Во-вторых, важна разрядность измерительного прибора, АЦП, Аналогово-Цифрового Преобразователя. Вот тут, к сожалению, я не смогу дать никаких рекомендаций. Почему-то во многих статьях, которые я прочитал, говорится о выборе частоты дискретизации по теореме Котельникова, но не говорится о разрядности АЦП. Это немного странно, так как сама теорема Котельникова подразумевает взятые отсчеты с абсолютной точностью, чего в реальной жизни быть не может. Еще нужно посмотреть на уровень шумов во входном сигнале, может вообще оказаться, что младшие разряды АЦП «дрожат». Вероятно, нет смысла брать АЦП с разрядностью допускающей «дрожание» нескольких младших битов из-за шумов во входном сигнале.
Так или иначе, после того, как входной сигнал оцифрован и представляет из себя поток чисел, его можно обрабатывать численными методами в микроконтроллерах или в ПЛИС.
Существуют фильтры низких частот (low-pass filter), которые пропускают только частоты ниже заданной частоты среза. Есть фильтры высоких частот (high-pass), которые наоборот, подавляют частоты ниже частоты среза. Бывают полосовые фильтры, которые пропускают или подавляют только частоты в заданной полосе (band-pass & band-stop filters).
Структура этого фильтра вот такая:
КИХ фильтр имеет несколько важных особенностей:
Вот тут все иначе. Здесь есть сумматор, который складывает входной сигнал с задержанным и умноженным на некоторый коэффициент выходной сигнал. У сумматора фиксированная разрядность. Понятно, что такой вычислитель может легко переполниться. Вот подать на такую цепь сигнал с постоянной составляющей, то через некоторое время гарантированно произойдет переполнение аккумулятора результата. Вот уже получается непредсказуемость и неустойчивость. Применять БИХ фильтры нужно с осторожностью, зараннее зная характер входного сигнала.
Теперь о быстродействии КИХ фильтра. Поскольку данные движутся только вперед, то довольно просто использовать преимущества конвейерной обработки. Например, пока умножители умножают очередные данные из задерживающих регистров, сумматор может вычислять сумму от предыдущих результатов умножителей. И сами умножители могут использовать внутренний pipeline и сумматор может использовать внутренний pipeline. Да, результат из фильтра получится задержанным на несколько тактов, но только и всего. Если же посмотреть на звено БИХ фильтра, как на рисунке выше, то понятно, что из-за обратной связи складывать нельзя, пока умножитель не вычислит свой результат.
Например, я хочу построить полосовой фильтр. Частота дискретизации 20МГц. Пусть фильтром нужно подавлять частоты ниже 1МГц и выше 4х МГц.
module fir ( clk, coefs, in, out );
parameter IWIDTH = 16; //input data (signal) width
parameter TAPS = 2; //number of filter taps
input wire clk;
input wire [IWIDTH-1:0]in;
genvar i;
generate
for ( i=0; i
begin:tap
//make tap register chain
reg [IWIDTH-1:0]r=0;
if (i==0)
begin
//1st tap takes signal from input
always @( posedge clk)
r
end
else
begin
//tap reg takes signal from prev tap reg
always @( posedge clk)
tap[i].r
end
end
endgenerate
endmodule
Конструкция generate-endgenerate языка Verilog позволяет динамически создать нужное число регистров и посоединять их как надо в цепочку. Получится вот так:
Таким образом, длина фильтра может быть задана через параметр модуля Verilog. Аналогичным образом, внутри цикла for() внутри generate-endgenerate создаются умножители:
genvar i;
generate
for ( i=0; i
begin :tap
.
//get tap multiplication constant coef
wire [CWIDTH-1:0]c;
assign c = coefs[((TAPS-1-i)*32+CWIDTH-1):(TAPS-1-i)*32];
//calculate multiplication and fix result in register
reg [MWIDTH-1:0]m;
always @( posedge clk)
m
.
Таким образом, дополнительно к регистрам линии задержки будут сформированы и подключены умножители со своими коэффициентами:
Я решил, что коэффициенты для умножителей можно передавать в модуль объединенные в шину <. >как входной сигнал, вот так:
Здесь каждый коэффициент фильтра занимает в шине фиксированное число бит 32 (решил, что этого должно хватить). Но из этих 32х бит модуль выберет нужное объявленное число бит для коэффициентов. Например, parameter CWIDTH = 16; Напомню, что от количества бит в коэффициенте для умножения зависит в конечном итоге ширина результата.
Для простоты реализации я пока не стал делать pipeline для сумматоров. Их можно было бы сделать побыстрее, например, складывать значения из умножителей попарно, потом складывать попарно результаты предыдущих парных сложений и так далее.. Пока я сделал один большой сумматор, как одну большую и сложную комбинаторную функцию. Наверняка в ПЛИС это не сможет работать на высоких частотах, но пока я на это закрываю глаза. Сделать бы чтобы просто работало.
Полный текст модуля будет выглядеть вот так:
Если будет время, то постараюсь улучшить этот модуль, добавить pipeline сумматоров.
Структура программы testbench.v:
Синусоиду для тестбенча я уже когда-то показывал. Возьму тот старый код, немного подправлю его и сделаю плавное изменение частоты от 100кГц до 4МГц с шагом в 1000Гц.
Внутрь тестбенча установлю два экземпляра модуля своего fir() фильтра, но с разными коэффициентами, для фильтра нижних частот и для полосового фильтра.
Весь код тестбенча вот здесь:
В результате симуляции программой vvp получается выходной файл с временными диаграммами сигналов out.vcd. Их можно посмотреть в программе GtkWave. Вот что видно: входной сигнал sin16 для обоих фильтров меняет частоту, она растет:
На широком диапазоне частот от сотен килогерц до нескольких мегагерц видно какие частоты пропускаются фильтрами, а какие подавляются:
А вот выходные сигналы, такие какие и положены быть на выходе фильтров. Фильтр низких частот от 500кГц начинается плавный спад амлитуды синусоиды out_lowpass и после 2х МГц фильтр уже практически не пропускает. Полосовой фильтр хорошо пропускает где-то в полосе 2-3МГц, а по краям пологие спады (сигнал out_bandpass).
Чтобы внимательно рассмотреть получившуюся картину нужно использовать специальные возможности просмотра в программа GtkWave. Вот несколько полезных советов:
Еще совет: GtkWave может отображать аналоговый сигнал отмасштабированный по высоте с учетом всех выборок симуляции по времени или с учетом только выборок, которые помещаются в окне. Если поставить Data Format => Analog => Resizing => Screen Data, то есть если масштабирование по вертикали будет учитывать только помещающиеся в окне выборки, то можно увидеть боковые лепестки амплитудно-частотной характеристики фильтра:
Таким образом, думаю мне удалось создать параметрический КИХ (FIR) фильтр и получилось посмотреть, как он работает.
Справедливости ради нужно сказать, что среда проектирования Altera Quartus II и Quartus Prime уже имеют встроенные мегафункции для FIR фильтров. Создать фильтр в среде Quartus по имеющимся коэффициентам довольно просто. Однако, имеющиеся мегафункции квартуса доступны в версиях Web Edition и Lite только для ознакомления. Они работают ограниченное время. Требуется приобретение полной версии САПР, чтобы применять FIR в своих проектах без ограничений.
Цифровая фильтрация на ПЛИС – Часть 2
Это вторая публикация на тему «Цифровая фильтрация на ПЛИС». Вторая часть будет посвящена практической реализации КИХ фильтров на FPGA. В процессе подготовки материала я понял, что она раздуется до небывалых размеров, но делить ее на несколько частей не хочется. Поэтому все тонкости теории и синтеза FIR фильтров будут в одной статье, разбитой на взаимосвязанные разделы. Начну обзор с теоретической части, в частности — расскажу об особенностях и методах расчета коэффициентов фильтров. Подробно рассмотрю создание КИХ фильтров в различных средах — MATLAB, CoreGENERATOR, Vivado HLS. Всех заинтересовавшихся прошу под кат.
Часть 2. КИХ фильтр
Теория
Рассмотрим простой пример реализации FIR фильтров. Как известно, существует два больших класса фильтров — БИХ, с бесконечной импульсной характеристикой и КИХ, с конечной импульсной характеристикой. Остановимся на втором типе: КИХ фильтрах (англ. FIR — «finite impulse response»). КИХ фильтр — это линейный цифровой фильтр, основной особенностью которого является ограниченность во времени его импульсной характеристики, то есть с определенного момента времени она становится равной нулю. Как правило, большинство КИХ фильтров выполнено без обратной связи, поэтому практически все КИХ фильтры — нерекурсивные.
Вот так выглядит реализация КИХ фильтра в общем виде, в частности — на ПЛИС.
Все КИХ-фильтры описываются следующими уравнениями: 
где y(n) — выходной сигнал (функция текущего и прошедших значений на входе), x(n) — входное воздействие, h(k) — коэффициенты импульсной характеристики, N — длина фильтра (количество коэффициентов фильтра), H(z) — передаточная характеристика фильтра.
В чем секрет КИХ фильтров?
Самая важная особенность КИХ фильтров заключается в возможности получения точной линейной фазовой характеристики. У читателя возникает закономерный вопрос — «а зачем это надо?». Остановимся на этом моменте подробнее. Сигнал подвергается различным преобразованиям при прохождении через фильтр. В частности, изменяются амплитуда и фаза сигнала в зависимости от частотной характеристики фильтра (амплитудной, АЧХ и фазовой, ФЧХ). Для многочастотных сигналов недопустимо, чтобы при прохождении блоков обработки, фаза сигнала искажалась. Причем, если АЧХ в полосе пропускания сделать практически постоянной не составляет труда, то с ФЧХ возникают проблемы. Для оценки искажений фазы удобно ввести понятия фазовой и групповой задержек.
Фазовая задержка — это величина задержки для каждой из частотных компонент сигнала. Определяется как угол сдвига фазы, деленный на частоту. Групповая задержка — это средняя временная задержка всего многочастотного сигнала. Определяется как производная фазы по частоте. Математически фазовая и групповая задержки записываются следующим образом: 
Из формулы для групповой задержки становится очевидно условие линейности ФЧХ фильтра. Если ФЧХ — линейна, то групповая задержка после взятия производной равна константе, то есть постоянна для всех частотных компонент. Логично, что фильтр с нелинейной ФЧХ будет вносить искажения в фазу сигнала.
Таким образом, линейность фазовой характеристики — одна из важнейших особенностей КИХ-фильтров. Остановимся на изучении этого класса фильтров.
КИХ фильтры с линейной ФЧХ
sin(x)/x независимо от типа фильтра (ФНЧ, ФВЧ, ПФ, РФ, дифференциатор). Для решения практических задач зачастую не приходится задумываться о том, какого типа фильтр выбран. Доказательство условия симметрии коэффициентов приводить не буду, но любопытный читатель может найти его сам в различной литературе, ссылки на которую я привожу в конце статьи.
Проектирование КИХ фильтров
Под «расчетом FIR фильтра» в большинстве случаев понимают поиск его коэффициентов по значениям частотной характеристики. Не могу припомнить случаев, когда решалась бы обратная задача за исключением академического интереса.
Вычисление коэффициентов фильтра
На эту тему можно написать несколько книг и научных статей, но в рамках данной статьи рассматривать подробно все методы не будем. Существует множество методов расчета коэффициентов фильтра — метод взвешивания оконными функциями, метод частотной выборки, различные оптимальные (по Чебышеву) методы с применением алгоритма Ремеза и т.д. Все методы уникальны по своим особенностям и дают те или иные результаты. Для метода оконного взвешивания негативным проявлением становится эффект Гиббса, вносящий неравномерность и выбросы в частотную характеристику фильтра между рассчитанными точками функции. Бороться с ним можно бесконечно, но на практике вводят допуски по неравномерностям в полосе пропускания и полосе подавления.
Основным методом расчета коэффициентов для многих фильтров является модифицированный алгоритм Ремеза — «Parks-McClellan algorithm». По своей сути это косвенный итерационный метод для нахождения оптимальных значений с Чебышевской характеристикой фильтра. Особенность метода заключается в минимизации ошибки в полосе затухания и пропускания путем Чебышевской аппроксимации импульсной характеристики. Вполне логично, что чем больше количество коэффициентов, тем меньше неравномерность АЧХ и тем она прямоугольнее.
От выбора метода зависит конечный результат, но все они сводятся к одним и тем же целям — минимизации выбросов в полосе пропускания и увеличении «прямоугольности» АЧХ.
Анализ следствий конечной разрядности
Разрядность коэффициентов — главный фактор, от которого зависит вид частотной характеристики. В современных ПЛИС разрядность коэффициентов может быть выбрана любой, но разумные цифры лежат в пределах от 16 до 27 битов. Для высоких порядков фильтра часто требуется обеспечить большой динамический диапазон разрядной сетки, но если этого не удается сделать, рано или поздно начинают проявляться ошибки квантования. Из-за ограниченной разрядности коэффициентов модифицируется частотная характеристика, а в некоторых случаях она искажается настолько сильно, что приходится жертвовать параметрами из частотной спецификации для достижения приемлемого результата. Так или иначе, разрядность представления коэффициентов прямо влияет на максимально возможное затухание Astop. Поэтому при использовании слишком ограниченной разрядной сетки коэффициентов, порой невозможно достичь желаемого подавления даже при огромных порядках фильтра!
Разрядность промежуточных данных и арифметическое переполнение — факторы, от которых также зависит вид частотной характеристики и результат на выходе фильтра. Во многих ПЛИС проблема устраняется использованием аккумуляторов большой разрядности в блоках DSP. Например, в ПЛИС Xilinx 6 и 7 серии в ячейках DSP48E1 используются 48-битные аккумуляторы и перемножители. На следующем рисунке представлен стандартный блок DSP48E1, на котором реализуются КИХ фильтры. 
Встроенные DSP блоки современных ПЛИС выполнены таким образом, чтобы максимально удобно проводить задачи ЦОС. В первую очередь — для реализации FIR фильтров.
Для реализации простейших фильтров требуется совсем немного логических операций. Основной узел, с помощью которого реализуется FIR фильтр — DSP блок ПЛИС. В этом блоке происходят все математические операции — перемножение входных отсчетов с коэффициентами фильтров, задержка входного сигнала, суммирование данных. Современные узлы DSP содержат предварительный сумматор, поэтому даже операции суммирования для фильтров с симметричной ИХ можно делать внутри этого узла. Помимо DSP блока, фильтру нужна память для хранения коэффициентов (распределенная или блочная). Больше фильтр ничего не использует. На рисунке приведена реализация КИХ фильтра с использованием перемножителей, аккумуляторов, линий задержки и памяти для хранения коэффициентов.
Расчет фильтра в MATLAB
Существует множество приложений, в которых можно проводить расчет фильтра и поиск его коэффициентов. Например, LABView, Scope FIR, FDATool из MATLAB или бесплатного аналога Octave. Пожалуй, самым удобным средством расчета КИХ фильтра является MATLAB. Для запуска средства создания и анализа фильтров необходимо в командном окне среды набрать ключевое слово fdatool. Появится примерно вот такое окно (в зависимости от версии MATLAB оно может иметь чуть иной вид):
Причем, в зависимости от типа фильтра, средство анализа укажет на ограничения по типу фильтра и предложит ввести корректное значение N.
*** — наибольший практический интерес представляют фильтры типа Equiripple и Window.
**** — при выборе этой опции появляется панель доступа к оконным функциям и их параметрам.
Для метода Equiripple производится самый простейший расчет КИХ фильтра по модифицированному алгоритму Ремеза. Пользователь задает параметры из спецификации на фильтр и сразу видит результат. В случае неудовлетворительных результатов можно в любой момент изменить один или несколько параметров фильтра и получить другую частотную характеристику. Расчет проводится до тех пор, пока не получены требуемые характеристики. Если не удалось добиться значений по заданию, то рано или поздно придется жертвовать той или иной величиной из спецификации, либо существенно увеличивать порядок фильтра N.
Для метода Window доступно несколько вариантов оконных функций: Bartlett, Blackman, Blackman-Harris, Chebyshev, Flat Top, Gaussian, Hamming, Hann, Kaiser, Rectangular и т. д., вплоть до пользовательских оконных функций (User-defined). Все эти функции обладают своими особенностями и могут давать различные параметры частотной характеристики КИХ фильтра. Часть оконных функций рассчитывается без параметров, а часть фильтров задается через определенные параметры, влияющие на АЧХ фильтра.
Из всех представленных оконных функций, на мой взгляд, самой удобной является окно Кайзера. Для построения АЧХ требуется задать всего один параметр Beta, который влияет на уровень подавления в полосе затухания и на прямоугольность частотной характеристики.
Слева снизу относительно главной рабочей области средство FDATool содержит дополнительные вкладки, в которых можно указать тип фильтра (дециматор или интерполятор), имя модели для вставки в Simulink, тип и разрядность коэффициентов и входных данных и многое другое. В практических целях самые основные вкладки это Design Filter — в ней происходит расчет фильтра, и Quantinization Parameters — в этой вкладке задается тип и разрядность данных.
На верхней панели находятся кнопки, с помощью которых можно посмотреть АЧХ и ФЧХ фильтра, групповую и фазовую задержку, импульсную и переходную характеристики, карту нулей и полюсов фильтра, рассчитанные коэффициенты и т.д.
График АЧХ и ФЧХ фильтра:
График импульсной характеристики фильтра:
График диаграммы нулей и полюсов:
Помимо всего этого, FDATool позволяет импортировать и экспортировать модели фильтров и рассчитанные коэффициенты. Например, можно рассчитать фильтр и отправить его модель в Simulink в виде модели на стандартных примитивах. Можно рассчитать коэффициенты и сохранить их в отдельном файле, например, как файл с расширением *.h (header).
Видно, что при подаче на вход единичного импульса, на выходе образуется не что иное, как импульсная характеристика фильтра (график из Simulink).
Xilinx FIR Compiler
Как и в случае с CIC фильтром, приведу подробное описание средства создания FIR фильтров от Xilinx. Отмечу, что описание содержит не просто перевод из даташита, а замечания и рекомендации из личного опыта и опыта моих коллег.
FIR Compiler — Вкладка 1:
Component name — имя компонента (используются латинские буквы a-z, цифры 0-9 и символ «_»).
Рекомендую использовать осмысленные имена, в которых зашифрованы главные параметры фильтра. Например, xfir128t_d1_b18_4c_w6_a7 — фильтр, сделанный для Xilinx, N = 128 (taps), децимация не используется, разрядность коэффициентов 18, четыре канала, применена оконная функция Кайзера с параметром beta = 6, кристалл ПЛИС — Artix-7.
FIR Compiler — Вкладка 2:
Summary — эта вкладка в виде списка отражает конечные настройки фильтра (количество каналов, порядок фильтра, параметры частот, разрядность входных, выходных и промежуточных данных, разрядность коэффициентов, задержка в фильтре, количество используемых DSP блоков, наличие сигналов контроля и т.д.).
Абстрактный пример
Шаг 1: Оценка ресурсов ПЛИС
Необходимо понять, сколько доступно ресурсов кристалла для реализации подобного фильтра. В DS180 можно найти, что микросхема имеет 240 DSP48E1 блоков, выстроенных в три колонки (это важно!). Из ТЗ известно, что ИХ – симметрична, а это значит, что для фильтра порядка N потребуется N/2 блоков DSP48E1. Следовательно, на выбранной микросхеме возможна реализация 2 фильтров с длиной характеристики N = 240, либо 6 фильтров с длиной N = 80. В практических целях при обработке сигналов длину ИХ выбирают кратному степени двойки. Например, N = 64, 128 или 256. Либо, N = (128 + 64), (32 + 16 + 8). В нашем случае необходимо реализовать 6 фильтров на 240 DSP блоках. С учетом симметрии для каждого фильтра возможно использовать длину N 0.85 найдем частоту заграждения Fstop Красивые рисунки разводки проекта
Схематический вид части IP-ядра FIR фильтра:
Разводки платы в FPGA Editor (Zoom нижней части):
Разводка платы в FPGA Editor:
Практические советы
Vivado HLS
В качестве примера я взял одну из лабораторных работ от Xilinx, в которой в первом приближении показана вся мощь современных средств. Основная разработка с помощью Vivado HLS базируется на взаимосвязанных задачах: написание кода и его оптимизация по скорости (Speed) и занимаемой площади (Area) с помощью директив.
Директивы в отдельном файле выглядят следующим образом:
Замечание: В процессе оптимизации разработчику часто приходится сравнивать различные результаты по производительности и ресурсам. Поэтому зачастую большая часть директив записывается в отдельный файл. Если разработчик уверен, что конкретная оптимизация нужна для всех решений, то её можно занести в исходные тексты!
Сравнение трех решений:
Директивы:
Вкладка Performance:
Вкладка Resources:
Процесс создания нового проекта и все шаги проектирования описывать не буду, поскольку статья и так уже разрослась до небывалых размеров. Но если вам интересна тема использования Vivado HLS в своих проектах – я с удовольствием поделюсь своим опытом. Также можно воспользоваться помощью хабраюзера urock. В этом деле он мастер!