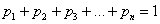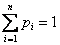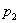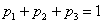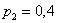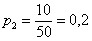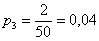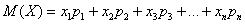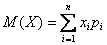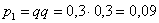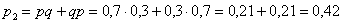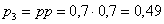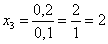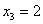Что такое дискретное распределение
Распределения вероятностей
Случайная переменная — это величина, которая может принимать любое из набора взаимоисключающих значений с определенной вероятностью.
Распределение вероятности показывает вероятности всех возможных значений случайной переменной. Это теоретическое распределение, которое выражено математически и имеет среднее и дисперсию — аналоги среднего и дисперсии в эмпирическом распределении.
Каждое распределение вероятности определяется некоторыми параметрами, параметры служат обобщающими величинами (например среднее, дисперсия), характеризующими данное распределение (т.e. их знание позволит подробно описать распределение).
С помощью соответствующей статистики можно произвести оценку этих параметров в выборке В зависимости от того, является ли случайная переменная дискретной или непрерывной, распределение вероятности может быть либо дискретным, либо непрерывным.
Дискретные распределения
Моделируют вероятность наступления дискретных событий, например, выпадение герба или решки (распределение Бернулли), число выпадений герба или решки при многократном бросании монеты (биномиальное распределение), выпадения определенного числа очков при бросании игральной кости (полиномиальное или мультиномиальное распределение).
Примеры дискретных величин самые разнообразные: число телефонных звонков за день, количество перевезенных пассажиров, количество дефектов в партии продукции, количество распавшихся атомов за определенный промежуток, число квантов света, попавших на сетчатку глаза и множество других в физике, технике, биологии, медицине, экономике, транспорте, телефонии.
Случайные величины. Дискретная случайная величина.
Математическое ожидание
Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через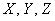 
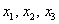
*, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, 
.
* Иногда используют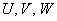 
, а также греческие буквы
Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:
– количество очков, которое выпадет после броска игрального кубика.
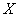
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина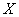 
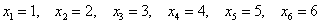
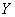
может принять одно из следующий значений:
.
– количество мальчиков среди 10 новорождённых.
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
, либо 
мальчиков – один и только один из перечисленных вариантов.
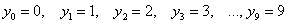
И, дабы соблюсти форму, немного физкультуры:
– дальность прыжка в длину (в некоторых единицах).
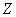
Её не в состоянии предугадать даже мастер спорта 🙂
Тем не менее, ваши гипотезы?
Коль скоро речь идёт о множестве действительных чисел, то случайная величина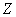 
может принять несчётно много значений из некоторого числового промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
…нарисовались непонятные термины? Срочно повторяем основы алгебры!
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную.
Закон распределения дискретной случайной величины
– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей: 
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».
А теперь очень важный момент: поскольку случайная величина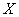 
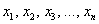
обязательно примет одно из значений 
, то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице: 
или, если записать свёрнуто: 
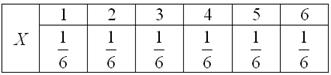
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид: 
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
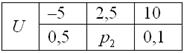
Некоторая игра имеет следующий закон распределения выигрыша: 
Найти 
…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.
Решение: так как случайная величина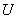 
может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице: 
Разоблачаем «партизана»: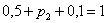 
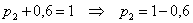
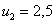
– таким образом, вероятность выигрыша 
условных единиц составляет 0,4.
Контроль: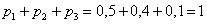 
, в чём и требовалось убедиться.
Ответ: 
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины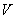 
– размера выигрыша, если из коробки наугад извлекается один билет.
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно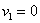 
рублей.
Всего таковых билетов 50 – 12 = 38, и по классическому определению:
– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.
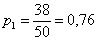
С остальными случаями всё просто. Вероятность выигрыша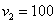 
рублей составляет: 
И для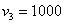 
: 
Проверка: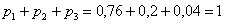 
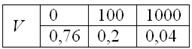
– и это особенно приятный момент таких заданий!
Ответ: искомый закон распределения выигрыша: 
Следующее задание для самостоятельного решения:
Вероятность того, что стрелок поразит мишень, равна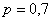 
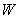
. Составить закон распределения случайной величины 
– количества попаданий после 2 выстрелов.
…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина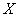 
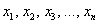
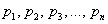
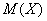
принимает значения 
с вероятностями 
соответственно. Тогда математическое ожидание 
данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:
или в свёрнутом виде: 
Вычислим, например, математическое ожидание случайной величины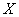 
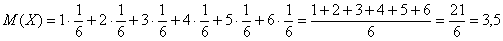
– количества выпавших на игральном кубике очков:
очка
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру: 
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
, таким образом, математическое ожидание данной игры проигрышно.
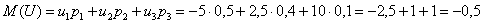
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины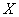 
– его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
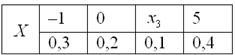
Случайная величина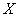 
задана своим законом распределения вероятностей: 
Найти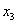 
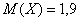
, если известно, что 
. Выполнить проверку.
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
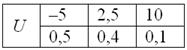
Пример 3. Решение: по условию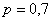 
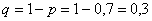
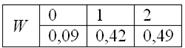
– вероятность попадания в мишень. Тогда:
– вероятность промаха.
Составим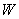 
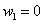
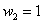
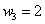
– закон распределения попаданий при двух выстрелах:
– ни одного попадания. По теореме умножения вероятностей независимых событий: 
– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий: 
– два попадания. По теореме умножения вероятностей независимых событий: 
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ: 
Примечание: можно было использовать обозначения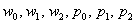 
– это не принципиально.
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: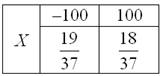 
Вычислим математическое ожидание: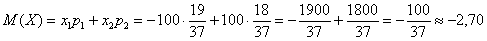 
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: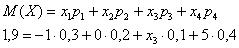 
поменяем части местами и проведём упрощения: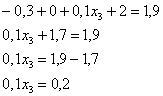 
таким образом: 
Выполним проверку: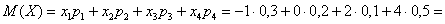 
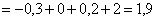
, что и требовалось проверить.
Ответ: 
Автор: Емелин Александр
(Переход на главную страницу)
Zaochnik.com – профессиональная помощь студентам
cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5
Tutoronline.ru – онлайн репетиторы по математике и другим предметам
Дискретное распределение
Опубликовано 22.06.2021 · Обновлено 22.06.2021
Что такое Дискретное распределение?
Дискретное распределение – это статистическое распределение, которое показывает вероятности дискретных (счетных) результатов, таких как 1, 2, 3 … Статистические распределения могут быть дискретными или непрерывными.
Непрерывное распределение строится из результатов, которые попадают в континуум, например, все числа больше 0 (включая числа, десятичные дроби которых продолжаются бесконечно, например 3,14159265 …). В целом концепции дискретных и непрерывных распределений вероятностей и описываемых ими случайных величин лежат в основе теории вероятностей и статистического анализа.
Понимание дискретного распределения
Краткая справка
Распределение должно быть дискретным или непрерывным.
Статистики могут определить развитие дискретного или непрерывного распределения по характеру результатов, которые необходимо измерить. Дискретные распределения имеют счетное количество результатов, что означает, что потенциальные результаты можно поместить в список. Список может быть конечным или бесконечным; распределение Пуассона – это дискретное распределение, список <0, 1, 2, …>которого бесконечен. Например, при изучении распределения вероятностей кубика с шестью пронумерованными сторонами список будет <1, 2, 3, 4, 5, 6>. Другой пример может включать подбрасывание монеты. Подбросив монетку, вы увидите список <Орел, Решка>.
Примеры дискретного распределения
Что такое дискретное распределение
тБУРТЕДЕМЕОЙС УМХЮБКОЩИ ЧЕМЙЮЙО УХФШ ПУОПЧОЩЕ ПВЯЕЛФЩ ЙЪХЮЕОЙС Ч ФЕПТЙЙ ЧЕТПСФОПУФЕК. нЩ ОЕ ВХДЕН, ЛБЛ РТБЧЙМП, ЙОФЕТЕУПЧБФШУС ФЕН, ЙЪ ЛБЛПЗП НОПЦЕУФЧБ ДЕКУФЧХЕФ ЖХОЛГЙС Й ЛБЛЙН ЙНЕООП ЬМЕНЕОФБТОЩН ЙУИПДБН УПРПУФБЧМСЕФ УЧПЙ ЧПЪНПЦОЩЕ ЪОБЮЕОЙС. оБУ ЮБЭЕ ВХДЕФ ЙОФЕТЕУПЧБФШ ФП, ОБ НОПЦЕУФЧЕ ЛБЛПК ЧЕТПСФОПУФЙ ЬФЙ ЪОБЮЕОЙС РТЙОЙНБАФУС. рТЙЧЕДЈН ОЕУЛПМШЛП РТЙНЕТПЧ УПЧЕТЫЕООП ТБЪОЩИ УМХЮБКОЩИ ЧЕМЙЮЙО, ЙНЕАЭЙИ ПДОП Й ФП ЦЕ ТБУРТЕДЕМЕОЙЕ ( ПДЙОБЛПЧП ТБУРТЕДЕМЈООЩИ ).
=1, ЕУМЙ = ЗЕТВ, Й =0, ЕУМЙ = ТЕЫЛБ;
=0, ЕУМЙ = ЗЕТВ, Й =1, ЕУМЙ = ТЕЫЛБ.
2. фПЮЛБ ОБХДБЮХ ВТПУБЕФУС ОБ ПФТЕЪПЛ [0, 1]. ч ЬФПН УМХЮБЕ ЕУФШ ПФТЕЪПЛ [0, 1] У УЙЗНБ-БМЗЕВТПК ВПТЕМЕЧУЛЙИ РПДНОПЦЕУФЧ Й НЕТПК мЕВЕЗБ. рТЕДМБЗБА ЮЙФБФЕМА ХВЕДЙФШУС, ЮФП ДЧЕ УПЧЕТЫЕООП ТБЪОЩЕ ЖХОЛГЙЙ: Й (ТБУУФПСОЙС ДП ХРБЧЫЕК ФПЮЛЙ ПФ МЕЧПЗП Й ПФ РТБЧПЗП ЛПОГПЧ ПФТЕЪЛБ УППФЧЕФУФЧЕООП) ПВМБДБАФ ПДЙОБЛПЧЩНЙ ЧЕТПСФОПУФСНЙ РТЙОЙНБФШ ЪОБЮЕОЙС ЧОХФТЙ МАВЩИ ВПТЕМЕЧУЛЙИ НОПЦЕУФЧ (ЧЕТПСФОПУФЙ, ТБЧОЩЕ НЕТЕ мЕВЕЗБ РЕТЕУЕЮЕОЙС НОПЦЕУФЧ Й [0, 1]). фБЛЙН ПВТБЪПН, ЬФЙ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ УОПЧБ ПДЙОБЛПЧП ТБУРТЕДЕМЕОЩ, ОП ОЕ ПДЙОБЛПЧЩ: ЙИ ЪОБЮЕОЙС УПЧРБДБАФ МЙЫШ РТЙ ПДОПН ЬМЕНЕОФБТОПН ЙУИПДЕ = 0.5 ( ОБТЙУПЧБФШ ЗТБЖЙЛЙ ЖХОЛГЙК Й ).
пРЙЫЕН ТБЪМЙЮОЩЕ ФЙРЩ ТБУРТЕДЕМЕОЙК УМХЮБКОЩИ ЧЕМЙЮЙО. чУС ЧЕТПСФОПУФОБС НБУУБ НПЦЕФ ВЩФШ УПУТЕДПФПЮЕОБ Ч ОЕУЛПМШЛЙИ ФПЮЛБИ РТСНПК, НПЦЕФ ВЩФШ «ТБЪНБЪБОБ» РП ОЕЛПФПТПНХ ЙОФЕТЧБМХ ЙМЙ РП ЧУЕК РТСНПК. ч ЪБЧЙУЙНПУФЙ ПФ ФЙРБ НОПЦЕУФЧБ, ОБ ЛПФПТПН УПУТЕДПФПЮЕОБ ЧУС ЕДЙОЙЮОБС ЧЕТПСФОПУФОБС НБУУБ, ТБУРТЕДЕМЕОЙС ДЕМСФ ОБ ДЙУЛТЕФОЩЕ, БВУПМАФОП ОЕРТЕТЩЧОЩЕ, УЙОЗХМСТОЩЕ Й ЙИ УНЕУЙ.
еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ ДЙУЛТЕФОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ДМС МАВПЗП
дЙУЛТЕФОПЕ ТБУРТЕДЕМЕОЙЕ ХДПВОП ЪБДБЧБФШ УМЕДХАЭЕК ФБВМЙГЕК, Ч ЛПФПТПК :
фПЗДБ ДМС МАВПЗП ЧЩРПМОЕОП:
оБЛПОЕГ, ТБУРТЕДЕМЕОЙЕ НПЦЕФ ВЩФШ ЧЩРХЛМПК МЙОЕКОПК ЛПНВЙОБГЙЕК ДЙУЛТЕФОПЗП, БВУПМАФОП ОЕРТЕТЩЧОПЗП Й УЙОЗХМСТОПЗП ТБУРТЕДЕМЕОЙК.
ч УЙМХ ОЕЪБЧЙУЙНПУФЙ УПВЩФЙК РПД ЪОБЛПН ЛБЦДПК ЙЪ ЧЕТПСФОПУФЕК,