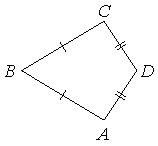
В выпуклом четырехугольнике abcd известно что ab равно bc
В выпуклом четырехугольнике abcd известно что ab равно bc
В выпуклом четырёхугольнике ABCD известно, что Найдите угол
Ответ дайте в градусах.
Проведем диагональ АС, получим два треугольника BAC и CAD. Рассмотрим треугольник ВАС, равнобедренный: угол ВАС = ∠BCA = x, получим уравнение:
Рассмотрим равнобедренный треугольник ACD, угол ACD = ∠CAD = у, составим уравнение:
Угол А равен сумме углов ВАС и CAD = 26 + 11 = 37°.
Аналоги к заданию № 509700: 511759 511779 Все
В выпуклом четырёхугольнике ABCD известно, что Найдите угол
Ответ дайте в градусах.
Проведем диагональ АС, получим два треугольника BAC и CAD. Рассмотрим треугольник ВАС, равнобедренный: угол ВАС = ∠BCA = x, получим уравнение:
Рассмотрим равнобедренный треугольник ACD, угол ACD = ∠CAD = у, составим уравнение:
Угол А равен сумме углов ВАС и CAD = 81,5 + 39,5 = 121°.
Аналоги к заданию № 509700: 511759 511779 Все
В выпуклом четырехугольнике abcd известно что ab равно bc
В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
Найдём косинусы углов ABC и ADC в треугольниках ABC и ADC соответственно:
Далее,
Тем самым сумма противоположных углов четырехугольника равна 180°, поэтому вокруг него можно описать окружность. Для вписанного четырёхугольника справедлива теорема Птолемея: произведение диагоналей четырёхугольника равно сумме произведений его противоположных сторон. Тогда то есть
откуда
Ответ: б)
Приведем решение пункта б) Тофига Алиева без использования теоремы Птолемея.
Заметим, что поскольку
Пусть
тогда в треугольнике BAD по теореме косинусов
В треугольнике BCD по теореме косинусов
Приведем идею решения Юрия Зорина.
Углы BAC и BDC равны как вписанные углы, опирающиеся на дугу BC. По теореме косинусов найдём косинус угла BAC (он равен 11/14). Далее, зная, что косинусы равных углов равны, из треугольника BDC найдем по теореме косинусов искомый отрезок BD.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, В выпуклом четырёхугольнике ABCD известны два углаФормулировка задачи: В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, ∠B, ∠D. Найдите угол A. Ответ дайте в градусах. Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии). Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения. В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, ∠B=61°, ∠D=151°. Найдите угол A. Ответ дайте в градусах. Соединим вершины четырехугольника A и C. Мы получили 2 равнобедренных треугольника, рассмотрим каждый из них. В треугольнике ABC ∠BAC и ∠BCA равны, т.к. это углы при основании равнобедренного треугольника. Сумма углов любого треугольника равна 180°. Поэтому: ∠BAC = ∠BCA = (180 – 61) / 2 = 59.5° В треугольнике ADC ∠DAC и ∠DCA равны, т.к. это углы при основании равнобедренного треугольника. Сумма углов любого треугольника равна 180°. Поэтому: ∠DAC = ∠DCA = (180 – 151) / 2 = 14.5° Осталось сложить ∠BAC и ∠DAC, чтобы получить ∠A: В общем виде решение данной задачи по планиметрии выглядит следующим образом: ∠A = ∠BAC + ∠DAC = (180 – ∠B + 180 – ∠D) / 2 = (360 – ∠B – ∠D) / 2 Остается лишь подставить конкретные значения и подсчитать результат. Поделитесь статьей с одноклассниками «В выпуклом четырёхугольнике ABCD известны два угла – как решать». Есть другой способ решения? Предложите другой способ решения задачи «В выпуклом четырёхугольнике ABCD известны два угла». Возможно, он окажется более понятным для кого-нибудь:
|