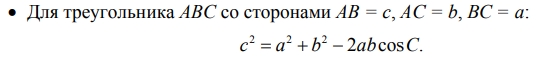В треугольнике абс известно что
В треугольнике абс известно что
В треугольнике ABC стороны AC = 37,5, BC = 20, угол C равен 90°. Найдите радиус вписанной окружности.
В треугольнике ABC известно, что 
угол C равен 
Найдите радиус вписанной окружности.
В треугольнике ABC известно, что 
угол C равен Найдите радиус вписанной окружности.
Именно так и вычислили
В треугольнике ABC стороны AC = 12, BC = 5, угол C равен 90°. Найдите радиус вписанной окружности.
В треугольнике ABC стороны AC = 24, BC = 10, угол C равен 90°. Найдите радиус вписанной окружности.
В треугольнике ABC 
угол C равен 90°. Найдите радиус вписанной окружности.
Это задание ещё не решено, приводим решение прототипа.
В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.
Приведем решение Айши Гучиговой.
Найдем гипотенузу треугольника: 
Площадь треугольника ABC равна 
С другой стороны, 
откуда
В треугольнике ABC 
угол C равен 90°. Найдите радиус вписанной окружности.
Это задание ещё не решено, приводим решение прототипа.
В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.
Приведем решение Айши Гучиговой.
Найдем гипотенузу треугольника:
Площадь треугольника ABC равна С другой стороны, откуда
В треугольнике ABC 
угол C равен 90°. Найдите радиус вписанной окружности.
Это задание ещё не решено, приводим решение прототипа.
В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.
Приведем решение Айши Гучиговой.
Найдем гипотенузу треугольника:
Площадь треугольника ABC равна С другой стороны, откуда
В треугольнике ABC 
угол C равен 90°. Найдите радиус вписанной окружности.
Это задание ещё не решено, приводим решение прототипа.
В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.
Приведем решение Айши Гучиговой.
Найдем гипотенузу треугольника:
Площадь треугольника ABC равна С другой стороны, откуда
В треугольнике ABC 
угол C равен 90°. Найдите радиус вписанной окружности.
Это задание ещё не решено, приводим решение прототипа.
В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.
Приведем решение Айши Гучиговой.
Найдем гипотенузу треугольника:
Площадь треугольника ABC равна С другой стороны, откуда
В треугольнике ABC 
угол C равен 90°. Найдите радиус вписанной окружности.
Это задание ещё не решено, приводим решение прототипа.
В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.
Приведем решение Айши Гучиговой.
Найдем гипотенузу треугольника:
Площадь треугольника ABC равна С другой стороны, откуда
Решение №1652 В треугольнике ABC известно, что AB=5, BC=10, AC=11.
В треугольнике ABC известно, что AB = 5, BC = 10, AC = 11. Найдите cos∠ABC.
Источник: ОГЭ Ященко 2022 (36 вар)
Из справочного материала ОГЭ используем теорему косинусов:
У нас АС = с (противолежащая искомому углу сторона), АВ = а, ВС = b, cos ∠B:
AC 2 = AB 2 + BC 2 – 2·AB·BC·cos∠АВС
11 2 = 5 2 + 10 2 – 2·5·10·cos∠АВС
121 = 125 – 100·cos∠АВС
100·cos∠АВС = 125 – 121
100·cos∠АВС = 4
cos∠АВС = 4/100 = 0,04
Ответ: 0,04.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 9
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
В треугольнике абс известно что
В треугольнике ABC биссектрисы AK и BL пересекаются в точке I. Известно, что около четырёхугольника CKIL можно описать окружность.
а) Докажите, что угол BCA равен 60°.
б) Найдите площадь треугольника ABC, если его периметр равен 12 и IC = 2.
а) Обозначим через α и β углы CAB и ABC соответственно. Тогда углы IAB и ABI равны 
и 
соответственно. По теореме о сумме углов треугольника получаем, что угол BIA равен 
Такая же величина у вертикального к нему угла LIK. По условию около четырёхугольника CKIL можно описать окружность. Следовательно, угол BCA дополняет угол LIK до 180°. С другой стороны, по теореме о сумме углов треугольника угол BCA дополняет до 180° сумму углов α и β. Следовательно, 
и 
Значит, угол BCA равен 60°.
б) Поскольку точка I является точкой пересечения биссектрис AK и BL, она также лежит на биссектрисе угла BCA и является центром вписанной в треугольник ABC окружности. Значит, радиус этой окружности равен длине перпендикуляра IH, опущенного из этой точки на BC. По доказанному угол HCI равен половине угла BCA, то есть он равен 30°. В прямоугольном треугольнике HCI против угла в 30° лежит катет IH. Следовательно, 
Площадь треугольника ABC равна половине произведения его периметра на радиус вписанной окружности. Значит, эта площадь равна 