В прямоугольном параллелепипеде абсда1б1с1д1 известно что аб 9 бс 8 аа1 6
Решение №1095 В прямоугольном параллелепипеде АВСDА1В1С1D1 известно, что АВ = 9, ВС = 8‚ АА1 = 6.
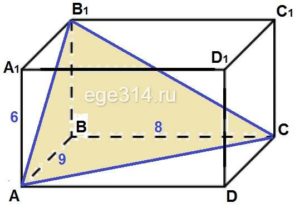
В прямоугольном параллелепипеде АВСDА1В1С1D1 известно, что АВ = 9, ВС = 8‚ АА1 = 6. Найдите объём многогранника, вершинами которого являются точки А, В, С, В1.
Многоугольник с вершинами А, В, С, В1 треугольная пирамида, объём находится по формуле:
Высота это ВВ1 = АА1 = 6.
Площадь основания – прямоугольного треугольника АВС:
Объём многоугольника:
Ответ: 72.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 6
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Решение №1070 В прямоугольном параллелепипеде АВСDА1В1C1D1 известно, что АВ = 9‚ ВС = 6 …
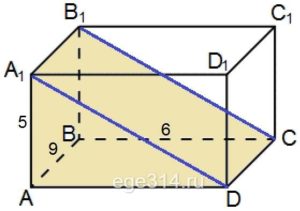
В прямоугольном параллелепипеде АВСDА1В1C1D1 известно, что АВ = 9‚ ВС = 6‚ АА1 = 5. Найдите объём многогранника, вершинами которого являются точки А, В, С, D, А1, В1.
Объём параллелепипеда АВСDА1В1C1D1 равен:
Объём многогранника, вершинами которого являются точки А, В, С, D, А1, В1 в два раза меньше объём параллелепипеда АВСDА1В1C1D1:
Ответ: 135.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
В прямоугольном параллелепипеде абсда1б1с1д1 известно что аб 9 бс 8 аа1 6
В прямоугольном параллелепипеде известно, что
Найдите длину ребра
По теореме Пифагора
Тогда длина ребра равна AB
В пространстве с L2-метрикой просто выражаете один из компонентов вектора через его длину, ну, типа,
Так мы так и делаем, только длину одной из компонент предварительно ищем по теореме Пифагора.
В прямоугольном параллелепипеде известно, что
Найдите длину ребра
По теореме Пифагора
Тогда длина ребра BA равна
В прямоугольном параллелепипеде известно, что
Найдите длину ребра
По теореме Пифагора
Тогда длина ребра CD равна
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. По условию даны длины двух измерений и длина диагонали. Осталось подставить в формулу и сосчитать.
На картинке показана диагональ BD1, ее подразумевают в решении, но пишут другую-DB1
Эти диагонали равны.
В прямоугольном параллелепипеде известно, что
Найдите длину ребра
По теореме Пифагора
Тогда длина ребра равна
Приведем другое решение.
В прямоугольном параллелепипеде известно, что
Найдите длину ребра
Найдем диагональ BD прямоугольника ABCD по теореме Пифагора:
Рассмотрим прямоугольный треугольник По теореме Пифагора
Таким образом,
В прямоугольном параллелепипеде известно, что
Найдите длину ребра
Это задание ещё не решено, приводим решение прототипа.
В прямоугольном параллелепипеде известно, что
Найдите длину ребра
Найдем диагональ BD прямоугольника ABCD по теореме Пифагора:
Рассмотрим прямоугольный треугольник По теореме Пифагора
В прямоугольном параллелепипеде абсда1б1с1д1 известно что аб 9 бс 8 аа1 6
На ребре BB1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка F так, что B1F : FB = 3 : 4. Точка T — середина ребра B1C1. Известно, что AD = 12, AA1 = 14.
а) Докажите, что плоскость FTD1 делит ребро AA1 в отношении 6 : 1.
б) Найдите площадь сечения параллелепипеда плоскостью FTD1.
б) Трапеция ED1TF — сечение параллелепипеда плоскостью ETD1. Найдём стороны трапеции:
Следовательно, трапеция ED1TF — равнобедренная. Найдём высоту трапеции:
Тогда площадь трапеции равна
Ответ: б)
| Критерии оценивания выполнения задания | Баллы | ||||||
|---|---|---|---|---|---|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 | ||||||
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 | ||||||
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, В прямоугольном параллелепипеде абсда1б1с1д1 известно что аб 9 бс 8 аа1 6В прямоугольном параллелепипеде ABCDA1B1C1D1 через диагональ BD1 проведена плоскость α, параллельная прямой AC. б) Найдите угол между проведённой плоскостью и плоскостью основания параллелепипеда, если AB = 6, BC = 8, CC1 = 10. б) Пусть B1M — перпендикуляр, опущенный из вершины B1 на прямую l. Тогда B1M — ортогональная проекция наклонной BM на плоскость A1B1C1D1. По теореме о трёх перпендикулярах прямые BM и l перпендикулярны, поэтому угол BMB1 — линейный угол двугранного угла, образованного секущей плоскостью α и плоскостью A1B1C1D1. Отрезок B1M вдвое больше высоты B1H прямоугольного треугольника A1B1C1, проведённой из вершины прямого угла, поэтому Из прямоугольного треугольника BMB1 находим, что Ответ: б)
|