В примере что сначала делать умножение или деление
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
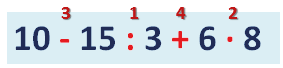
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Порядок выполнения действий
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
Полностью пример записываем так:
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Вывод:
Поделись с друзьями в социальных сетях:
Зубодробительная задачка с очень простой математикой
Эта задача поставит в тупик половину интернета, но не вас.
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать. Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами 🙂
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!

А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.

Что сперва умножение или деление
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать. Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами 🙂
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!
А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя.
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
Вычислим значение выражения.
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Выполнение тренировочных заданий на изученное правило
Рассмотрим выражения, установим порядок действий и выполним вычисления.
Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Узнаем, правильно ли определен порядок действий в следующих выражениях.
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 – 9 = 1
Сначала выполняем действия в скобках:
16 – 2 · 7 + 4 = 16 – 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Выполняем действия в круглых скобках, имеем:
8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4
действия в квадратных скобках дают:
14 – 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Порядок действий:
30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150