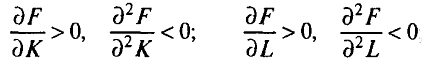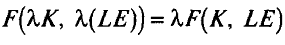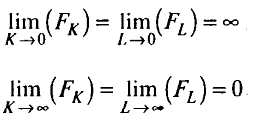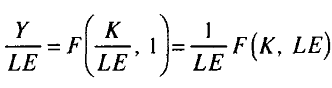В модели солоу предполагается что государство

Модель Солоу

Вы будете перенаправлены на Автор24

Неоклассическое направление в экономике

Экономическая наука строилась на базе изучения хозяйственных процессов в обществе. Многие ученые, философы, богословы занимались описанием событий бытовой жизни и экономики. Постепенно стали появляться школы, которые придерживались определенной позиции относительно устройства хозяйственных систем. Они строили гипотезы, пробовали анализировать закономерности экономических структур. К середине девятнадцатого века экономика окончательно оформилась в отдельное научное направление. Этому способствовал переход от нормативного подхода, к позитивному. Одной из школ нового поколения экономистов стала неоклассическая школа.

Она появилась в 1870 году. Яркими учеными неоклассического направления были:

В неоклассическом направлении человек рассматривается, в качестве рационального существа, постоянно стремящегося к максимизации собственной выгоды. Причем, в качестве индивида рассматриваются предприниматели, домохозяйства и наемные рабочие.

Цена рассматривается в рамках установления равновесия между предложением и спросом, а также, с точки зрения предельной полезности, которую конкретное благо может принести индивиду. Основное отличие от классиков заключается в том, что цена формируется благодаря спросу, а не производственному предложению.

Неоклассики так же, как и представители классической политэкономии, придерживаются позиции экономического либерализма и свободной конкуренции. То есть, они против всестороннего государственного вмешательства в хозяйственные процессы. При этом неоклассики стремятся решить практические задачи, путем применения математических методов и количественного анализа. Здесь большое внимание уделяется вопросам, заботящим экономическую теорию по сей день. Предметом изучения неоклассической школы является удовлетворение потребностей социума в условиях ограниченности ресурсов. Неоклассики применяют этот подход для микроэкономических систем – домохозяйств и предприятий. Можно сказать, что современная экономическая наука выстроилась на основе неоклассического направления.

Готовые работы на аналогичную тему

Модель Солоу

Многие ученые прибегали к методу моделирования с целью описания сложнейших экономических процессов, включавших в себя множество элементов. Для упрощения построения подобных структур и отслеживания закономерностей внутри них, экономисты прибегают в некоторым допущениям и обобщениям. Большое внимание ученых привлекали процессы, способствующие экономическому росту. Так, одной из моделей, пытающихся объяснить причины и методы формирования позитивных тенденций в хозяйственной системе, является модель Солоу.

Модель Солоу представляет собой анализ экономического роста с учетом влияния внешнего технического прогресса, а также воздействия производственных факторов – капитала и труда. Можно выделить три основных цели данной модели:

В общем виде модель Солоу представлена на графике:

Рисунок 1. Модель Солоу. Автор24 — интернет-биржа студенческих работ

Стоит отметить, что с течением времени производительная отдача капитала падает, поэтому предприниматели стараются пополнять объемы собственного капитала. Рост соотношения капитала к труду всегда сопровождается выбытием первого, чтобы этого не произошло, необходимо наращивать приток инвестиций. Хозяйственное равновесие модели Солоу достигается при остановке роста показателей выбытия капитала, уровня потребления и объема инвестиций. Такое состояние называется предельным уровнем капиталовооруженности, когда все три перечисленных параметра стабилизируются.

Сущность модели Солоу

Основной задачей экономистов является поиск решений для решения практических задач в области экономической политики. Модель Солоу помогает найти такой уровень производства, который сможет максимизировать потребительскую способность общества в условиях текущего темпа экономического роста. Такая модель носит название золотого правила накопления.

Предельное потребление формируется только тогда, когда достигается максимальная разница между выбытием капитала и выпуском, при стабильном показателе капиталовооруженности. Получается, что максимального объема потребления можно достичь только тогда, когда предельная капиталоотдача будет равна темпам производственного прироста.

Фактор демографического роста, как и выбытие капитала уменьшает его запасы. Увеличение количества людей снижает производительность труда одного сотрудника. Для того, чтобы компенсировать данные потери необходимо увеличить объем инвестиций с учетом прироста населения. Объем потребления так же будет иметь тенденцию к снижению. Модель Солоу показывает, что при высоком темпе прироста населения, снижается показатель капиталовооруженности, а значит, уменьшается доход на одного человека.

Технический прогресс, прежде всего, влияет на производственную отдачу труда. Модель Солоу показывает, что усложнение и использование более высоких технологий в производстве способно сбалансировать инвестиции, капитал и производительность в долгосрочном периоде.

Источник

Модель Солоу

Модель Солоу исследует влияние на экономический рост сбережений, роста населения и технологического прогресса. Модель экономического роста Солоу является необходимой отправной точкой практически всех исследований экономического роста. С ее помощью выявляются причины временного и постоянного, устойчивого роста экономики и существования различий в уровне жизни населения разных стран.

В модели рассматриваются четыре переменные: выпуск Y, капитал К, труд L и Е — уровень «знаний», накопленных в обществе.

Выпуск Y может изменяться во времени только при изменении факторов производства: К, L, Е. Если научно-технический прогресс способствует совершенствованию технологии в целом, не изменяя соотношения предельных производительностей капитала и труда, Y = EF(K, L),то такой прогресс носит название «нейтральный по Хиксу». Если же он способствует увеличению производительности капитала Y= F(KE, L), то он называется капиталосберегающим (прогресс по Харроду).

В модели Солоу переменная Е отражает эффективность труда одного работника, зависящую от состояния его здоровья, образования и квалификации.

Изменение численности работников и эффективности труда Е всегда рассматриваются совместно: в каждый момент времени t в экономике насчитывается Lt, работников с возросшей эффективностью труда или возросшее число работников с постоянной (начальной) эффективностью труда (Lt,Et). Таким образом, выпуск описывается производственной функцией Yt= F(Kt, LtEt). Это означает, что в модели Солоу предполагается так называемый трудосберегающий тип научно-технического прогресса, под влиянием которого повышается эффективность труда одного работника.

Рассматривается неоклассическая производственная функция, т. е. предполагается, что выполняются следующие свойства:

ü положительная и убывающая предельная производительность факторов:

ü несущественность влияния других факторов производства, в частности земли и природных ресурсов;

ü постоянная отдача от масштаба. Содержательно такая предпосылка соответствует достаточно большой экономике, для которой выигрыш от специализации уже исчерпал себя, и поэтому новые факторы производства используются тем же технологическим способом, что и уже существующие.

ü условие Инада: если капитал (или труд) бесконечно мал, то его предельная производительность бесконечно велика; если капитал (или труд) бесконечно велик, то его предельная производительность бесконечно мала.

Перечисленные свойства предполагают, что каждый фактор необходим для производства F(K, 0) = F(0, LE) = 0 и выпуск неограниченно растет при неограниченном росте каждого фактора.

Предположение о постоянной отдаче от масштаба позволяет перейти к производственной функции в интенсивной форме — в расчете на единицу труда с постоянной эффективностью:

Таким образом, выпуск в расчете на единицу труда с постоянной эффективностью зависит только от уровня капиталовооруженности и не зависит от масштаба экономики.

Для производственной функции в интенсивной форме сохраняются все вышеперечисленные свойства.

Источник

Неоклассическая модель экономического роста Солоу и золотое правило накопления

Цель данной модели – ответить на очень важные вопросы экономической теории и экономической политики; [1] каковы факторы сбалансированного экономического роста; какой темп роста может позволить себе экономика при заданных параметрах экономической системы и как при этом максимизировать доход на душу населения и объем потребления; какое влияние на темпы роста экономики оказывают рост населения, накопление капитала и технический прогресс. Модель Солоу показывает не только возможность равновесного экономического роста при полной занятости и полном использовании производственных мощностей. Особенностью этой неоклассической модели является и то, что она демонстрирует устойчивость экономического роста, т.е. способность экономической системы возвращаться к траектории сбалансированного развития при помощи внутренних рыночных механизмов саморегулирования.

Рис. 1. Производственная функция у = f(k). Данная функция построена из расчета на одного работника и характеризуется понижающейся предельной производительностью капитала МР_К

Скачать заметку в формате Word или pdf

Предпосылки модели:

Построение модели

Разделив двухфакторную производственную функцию Y = f(К, L) на количество труда L, мы получим производственную функцию для одного работника: у = f(k), где k = K/L – уровень капиталовооруженности единицы труда, или одного работника Доход (y = Y/L) предстает как функция только одного фактора – капиталовооруженности (k). Такая единичная производственная функция, отражающая средний уровень производительности труда, показана на рис. 1. Заметим, что крутизна ее наклона, определяемая величиной предельной производительности капитала МР_К, изменяется. По мере увеличения количества капитала на одного работника, предельная производительность этого фактора уменьшается (в соответствии теорией предельной производительности факторов [4]), что и вызывает замедление роста функции дохода.

Часть дохода Y используется на потребление, а другая часть сберегается. В модели Солоу, где все макроэкономические показатели рассчитываются на одного работника, сбережения тоже будут представлять собой часть единичного дохода sy или sf(k), где s — норма сбережения, определяющая, какая часть дохода сберегается.

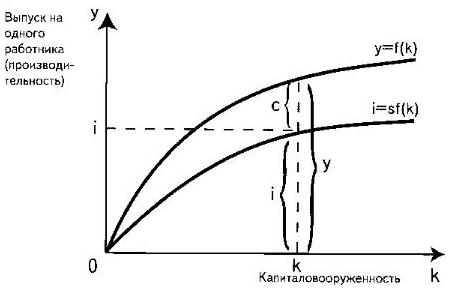
Условием макроэкономического равновесия является равенство совокупного спроса (AD) и совокупного предложения (AS), что автоматически приводит нас к макроэкономическому равенству I = S (объем инвестиций равен объему сбережений). Все сбережения в экономике полностью инвестируются, и это позволяет приравнять функцию фактических инвестиций на одного работника (i) к единичной функции сбережений: i = sy = sf(k). Помня о макроэкономическом равенстве Y = С + I (доход равен сумме потребления и сбережения), выпуск в расчете на одного занятого можно записать в виде у = с + i, где у = Y/L, с = C/L, i = I/L, а функцию потребления представить как с = у – i = f(k) — sf(k).

Графически размер потребления и инвестиций при каждом уровне капиталовооруженности изображены на рис. 1. Кривой sf(k) обозначен график фактически осуществленных инвестиций, которые по условию модели равны сбережениям. Поскольку сбережения составляют некую определенную долю от выпуска, то и фактически осуществленные инвестиции на душу населения представлены графиком, лежащим ниже графика производственной функции y = f(k) на рис. 1. Расстояние между графиками функций f(k) и sf(k) определяет объем потребления (c). Таким образом, функция потребления описывается формулой: с = f(k) – sf(k).

По условию модели Солоу, экономика изначально находится в состоянии устойчивого равновесия. Это значит, что планируемые, или требуемые инвестиции I равны фактически осуществленным инвестициям, т.е. сбережениям S. [5] В модели Солоу оно описывается, как устойчивое, или стационарное состояние экономики, при котором объем капитала на одного работника постоянен. Для определения стационарного состояния экономики в модели Солоу необходимо рассмотреть и проблему накопления капитала. Очевидно, для того, чтобы капиталовооруженность оставалась неизменной при условии роста населения, необходимо, чтобы капитал К увеличивался тем же темпом n, что и рост населения L. Таким образом, требуемые инвестиции в расчете на одного работника i r (верхний индекс r у символа инвестиций i – от английского слова required – требуемый) можно записать в виде следующего равенства: i r = nk. При этом если темп роста населения и темп накопления капитала равны, то выпуск на душу населения у остается неизменным.

Не будем забывать, что для описания чистого прироста капитала нужно учесть выбытие капитала, или амортизацию. Растущего капитала должно быть достаточно не только для оснащения новыми капитальными благами дополнительной рабочей силы, но и для пополнения выбывающего капитала. Обозначим норму выбытия (норму амортизации) символом δ. Таким образом, требуемые инвестиции в расчете на одного работника будут записаны в виде равенства i r = (n+δ)k. С учетом постоянного темпа роста населения и постоянной нормы выбытия можно в формализованном виде записать условия накопления капитала: Δk = sf(k) – (n+δ)k. Итак, мы имеем все необходимые данные, для того, чтобы объяснить механизм установления стационарного состояния в модели Солоу.

В ходе производства ежегодно пополняются капитальные запасы, независимо от того, с каким объемом капитала экономика начинает развиваться. Однако прирост фактических инвестиций, отображаемый графиком sf(k), идет затухающими темпами (рис. 2). Это объясняется уже рассмотренным выше снижением предельной производительности капитала МР_К, происходящим по мере увеличения капиталовооруженности одного работника. Но наращивание капиталовооруженности увеличивает и объем требуемых инвестиций, представленных на рис. 2 прямой линией (n+δ)k. Угол наклона этой линии равен величине (n+δ). С ростом производства разница между сбережениями (фактически осуществленными инвестициями) sf(k) и требуемыми инвестициями (n+δ)k будет уменьшаться до тех пор, пока эти величины не выровняются между собой. Когда Δk = 0, тогда производство, сбережения и требуемые инвестиции достигают определенного устойчивого уровня, т.е. экономика достигает состояния равновесия. Уровень капиталовооруженности, при котором Δk = 0, называется устойчивым уровнем капиталовооруженности (k*) и характеризует состояние равновесия экономики. В равновесном состоянии объем выпуска не изменяется, а сбережения и требуемые инвестиции равны: sf(k*) – (n+δ)k* = 0 или sf(k*) = (n+δ)k*.

Рис. 2. Определение устойчивого уровня капиталовооруженности

Таким образом, на рис. 2 пересечение графика сбережений sf(k) и графика требуемых инвестиций (n+δ)k будет показывать состояние равновесия, определяя величину устойчивого уровня капиталовооруженности k*.

Каков же в модели Солоу механизм, который обеспечивает равновесный рост? Для этого обратимся вновь к рис. 2. В точке k₁ сбережения превышают уровень требуемых инвестиций. Предложение капитала превышает спрос на него, т.е. объем капитала в точке k₁ является избыточным. В условиях гибких цен начнется процесс удешевления этого фактора производства по сравнению с трудом и таким образом начнется переход к более капиталоемким технологиям. Динамическое равновесие оказывается устойчивым, поскольку изменение относительных цен на факторы производства будет «подталкивать» экономику к состоянию устойчивой капиталовооруженности k*.

В случае, когда уровень капиталовооруженности соответствует точке k₂, инвестиции превышают сбережения. Возникающий дефицит капитала в условиях гибкого ценового механизма приведет к повышению цен на этот фактор производства, и начнется переход к менее капиталоемким технологиям вплоть до уровня k*.

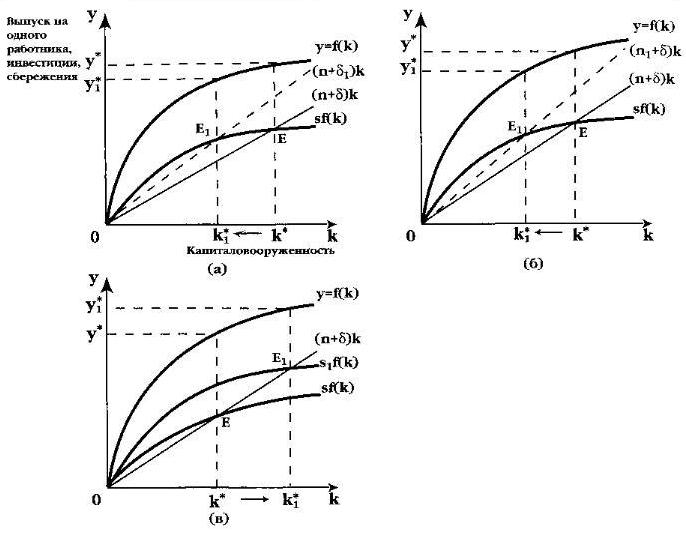
Как повлияет на устойчивый уровень капиталовооруженности и выпуск продукции на душу населения изменение нормы выбытия (δ), темпов роста населения (n) и нормы сбережений (s)? На рис. 3 показаны последствия изменений. Для уяснения работы модели Солоу нужно иметь в виду, что налогово-бюджетная и кредитно-денежная политика государства, а также институциональные и психологические факторы могут повлиять на уровень k* через воздействие на норму сбережения s или на норму амортизации δ, от величины которой зависит скорость обновления капитала. Например, политика ускоренной амортизации (рис. 3а) выразится в смещении графика (n+δ)k до уровня (n+δ₁)k. При этом устойчивый уровень капиталовооруженности снизится c k* до k₁* так же, как снизится и выпуск на душу населения с y* до y₁*.

Рис. 3. Влияние параметров модели на устойчивый уровень капиталовооруженности; изменяется: (а) норма выбытия (амортизации) δ; (б) темпы роста населения n; (в) норма сбережений s

Если же увеличится темп роста населения до n₁ (рис. 3б), то объем накопленного капитала распределится на большее количество занятых, и уровень устойчивой капиталовооруженности уменьшится до k₁*. Кривая требуемых инвестиций сместится из положения (n+δ)k в положение (n₁+δ)k. Одновременно уменьшится и выпуск на душу населения. Это позволяет объяснить низкий уровень подушевого дохода во многих развивающихся странах. Темп роста населения в беднейших странах мира гораздо выше, чем в промышленно развитых странах. Низкая норма сбережения, характерная для этих стран, не позволяет компенсировать последствия высоких темпов роста населения для уровня капиталовооруженности. Не случайно в таких условиях, если оставить в стороне нравственные оценки, снижение уровня рождаемости представляется чуть ли не самым главным способом повышения благосостояния населения.

Увеличение нормы сбережений в силу различных причин (увеличение склонности к сбережению под влиянием различных факторов психологического, институционального характера, а также под влиянием косвенных методов государственного регулирования) от уровня s до s₁ как видно из рис. 3в, наоборот, приведет к повышению равновесного уровня капиталовооруженности до k₁* в результате смещения графика сбережения до уровня s₁f(k). Таким образом, можно сделать вывод, что более высокая норма сбережения, при прочих равных условиях, ведет к большему объему накопления капитала и к более высокому уровню выпуска на душу населения. Это статистически подтверждено исследованиями многих экономистов. Так, к странам с самым высоким годовым доходом (в долларах США по текущему курсу, на 2000 г.) относятся США ($ 36 611), Великобритания ($23 868), Германия ($22 841), Франция ($22 006), Италия ($18 645), Япония ($37 571). На протяжении последних трех десятилетий XX века в этой группе стран норма сбережений была наиболее высокой (в среднем около 23% от ВВП) по сравнению со странами, где доходы ниже. В странах со средним уровнем подушевого дохода сберегалось от 20% до 22% ВВП, а в странах с низким уровнем дохода на душу населения – от 10% до 19% ВВП.

Однако мы должны особо подчеркнуть важный вывод, который делает Солоу: увеличение нормы сбережений лишь в краткосрочном периоде увеличивает темп роста выпуска. Иными словами, во время перехода с кривой sf(k) на кривую s₁f(k) (рис. 3в) темпы роста выпуска повышаются по сравнению с прежним стационарным состоянием экономики. При переходе из точки Е в точку Е₁ устойчивый уровень капиталовооруженности повысился с k* до k₁* при новом стационарном состоянии экономики. В силу каких причин это могло произойти? Ответ достаточно прост: уровень капиталовооруженности может увеличиться только в том случае, когда запас капитала растет более высоким темпом, чем предложение труда и выбытие капитала. Но увеличение нормы сбережения не влияет на долгосрочный темп роста выпуска, а только увеличивает уровень капиталовооруженности и объем подушевого дохода в долгосрочном плане.

Этот вывод может показаться неожиданным и противоречащим факту тесной взаимосвязи инвестиций и экономического роста. Объяснением этого кажущегося противоречия может быть то, что стационарное состояние экономики присуще далеко не всем странам. Если экономика не характеризуется состоянием равновесия, то она переживает процесс развития, а процесс этот может оказаться весьма продолжительным.

Модель Солоу интересна и тем, что помогает определению путей максимизации потребления при заданных темпах экономического роста. Возможность поддерживать уровень потребления на максимально высоком уровне – это своеобразный «эликсир политического долголетия» власти. Достижение высокого уровня потребления отвечает интересам любого электората. Однако, как видно из графика на рис. 3в, устойчивому состоянию экономики могут соответствовать разные нормы сбережений. Какая же норма сбережения максимизирует объем потребления при заданном темпе роста численности населения и неизменной технологии?

Условие, при котором достигается этот уровень потребления, вывел американский экономист Эдмунд Фелпс и назвал его золотым правилом накопления в своей работе «Басня для тех, кто занимается ростом» (1961 г.)

Рассмотрим графическое изображение золотого правила накопления. В соответствии с золотым правилом, самый высокий уровень потребления достигается при таком устойчивом уровне капиталовооруженности, который, как видно на рис. 4 соответствует наибольшему разрыву между объемом выпуска f(k*) и объемом требуемых инвестиций (n+δ)k *. Именно в этом случае в точке Е объем требуемых инвестиций (n+δ)k * совпадает с объемом сбережений sf(k*). Расстояние АЕ и показывает наибольший объем потребления. Поэтому уровень потребления с** в соответствии с золотым правилом называется устойчивым уровнем потребления: c** = f(k*) – (n+δ)k *

Рис. 4. Золотое правило накопления. Наклон графика производственной функции y = f(k) измеряется предельной производительностью капитала, МР_K, а наклон графика требуемых инвестиций измеряется темпом роста населения и нормой выбытия капитала (n+δ). В точке А, соответствующей устойчивому уровню капиталовооруженности k**, наклон графика производственной функции равен наклону графика требуемых инвестиций и при этом объем потребления максимален

Запас капитала, обеспечивающий устойчивое состояние при максимальном потреблении, называется золотым уровнем накопления капитала (k**). Именно при уровне k** наклон графика производственной функции у = f(k), измеряемый наклоном касательной в точке А, равен наклону графика требуемых инвестиций sf(k). Иными словами, предельная производительность капитала МР_K должна быть равна темпу экономического роста (n+δ). Это и есть само золотое правило накопления: МР_K = (n+δ).

До настоящего времени мы абстрагировались от фактора технического прогресса. Теперь же мы должны посмотреть, как изменятся условия стационарного роста с введением этой переменной. Термин «технический прогресс» в моделях экономического роста понимается в очень широком смысле, а именно, в смысле всех факторов, которые при заданных объемах труда L и капитала К позволяют увеличить национальный доход, или выпуск У.

Главное, на что мы должны обратить внимание – это сдвиг производственной функции Y = f(K,L), которая превращается в функцию, зависящую от переменной t, т.е. от времени: Y = f(K,L,t). В результате технического прогресса происходит сдвиг производственной функции в расчете на одного занятого из положения у₁ = f(k) в положение у₂ = f(k) (рис. 5). Сдвиг производственной функции может происходить под влиянием самых различных факторов: улучшения качества физического капитала, качества рабочей силы (рост квалификации работников), совершенствования структуры производства, совершенствования менеджмента и т.д.

Рис. 5. Влияние технического прогресса на устойчивый уровень капиталовооруженности и выпуск на душу населения

На рис. 5 вместе со сдвигом графика производственной функции из положения у₁ = f(k) в положение у₂ = f(k) происходит и сдвиг графика сбережений (фактических инвестиций) из положения s₁f(k) в положение s₂f(k). Технический прогресс приводит к тому, что устойчивый уровень капиталовооруженности перемещается из точки k₁* в точку k₂*. Равновесный уровень требуемых инвестиций и сбережений перемещается из точки E₁ в точку Е₂. Соответственно, устойчивый уровень выпуска на душу населения повышается от уровня у₁* до уровня у₂*.

В макроэкономической теории рассматриваются различные типы технического прогресса, характеризующиеся устойчивым уровнем капиталовооруженности. При исследовании модели Солоу мы будем исходить из так называемого нейтрального технического прогресса. Это означает, что при росте капиталовооруженности труда k предельная производительность капитала МР_К не снижается, как это могло бы произойти в отсутствие технического прогресса (см. рис. 1). Причина этого заключается в том, что рассматриваемый тип технического прогресса как бы увеличивает количество занятых тем же темпом, каким растет капитал. Воздействие этого типа технического прогресса на экономический рост связано с приростом эффективности труда А, идущего постоянным темпом g. Собственно, показатель g и предстает как темп технического прогресса. Тогда общее количество эффективного труда составит AL и, с учетом темпа роста населения и темпа роста эффективности труда, будет расти темпом n + g. Еще раз подчеркнем, что показатель AL является выражением неких условных единиц труда, а не физически занятых в производстве людей. Можно объяснить идею трудосберегающего технического прогресса и несколько по-иному. Поскольку эффективность и производительность труда – одно и то же понятие, то мы можем говорить не об условных единицах труда, а о том, что AL означает увеличение выпуска при том же количестве труда, в чем и заключается трудосбережение. Количество труда остается прежним при большем выпуске, поэтому и не изменяется устойчивый уровень капиталовооруженности.

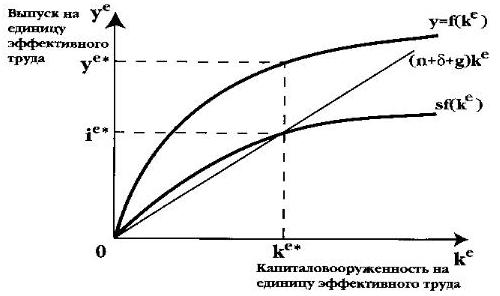
Поясним идею рассматриваемого типа технического прогресса на условном цифровом примере. Так, допустим, что в некоем исходном состоянии t₀ в экономике занято 1000 человек. Если прирост эффективного труда А идет темпом, равным темпу технического прогресса 3%, то те же самые 1000 занятых произведут в следующем периоде t₁ продукции столько, сколько произвели бы 1030 занятых. Теперь, с учетом фактора технического прогресса, идущего темпом g, мы можем представить модифицированную модель роста Солоу (рис. 6). Заметим, что темп роста запасов капитала теперь, с учетом технического прогресса, составит n + δ + g, т.е. именно этими величинами измеряется наклон графика требуемых инвестиций в расчете на единицу эффективного труда.

Рис. 6. Модель роста Солоу с учетом технического прогресса

Рис. 7. Золотое правило накопления с учетом технического прогресса

Итак, максимальный устойчивый уровень потребления с e ** (расстояние между точками А и Е) гарантируется таким объемом накопления k e **, который достигается при выполнении золотого правила с учетом роста населения и технического прогресса: МР_К = n + δ + g.

Мы рассмотрели влияние технического прогресса на устойчивый уровень капиталовооруженности k e **(в расчете на единицу эффективного труда) и пришли к следующему выводу: выпуск в расчете на единицу эффективного труда в стационарном состоянии остается неизменным. Действительно, если выпуск Y растет темпом n + g (2% + 3%), и AL растет тем же темпом, то, используя условный цифровой пример, получим следующее: в период t₀ выпуск объемом 10 000 ден. ед приходился на 1000 занятых. Тогда выпуск в расчете на одного занятого составил в период t₀ 10000/1000 = 10 ден. ед. Но, если выпуск растет темпом n + g, т.е. увеличивается на 5% (2% + 3%), то в следующий период времени t₁, он составит 10500 ден. ед. Выпуск в расчете на единицу эффективного труда (у e ) не увеличился – ведь AL растет тем же темпом n + g, т.е. теперь как бы трудятся 1050 человек. В расчете на одну единицу эффективного труда получаем: 10500 ден. ед./1050 = 10 ден. ед.

В чем же тогда проявляется воздействие технического прогресса на повышение благосостояния населения? Каким образом экономический рост, сопровождаемый техническим прогрессом, приводит к увеличению выпуска и потребления на душу населения? Для ответа на эти вопросы не следует забывать, что физически в периоде времени t₁, работали (с учетом темпа роста населения, равным в нашем примере 2%) 1020 человек, поэтому выпуск на душу (у) увеличился: 10500/1020 = 10,29 ден. ед.

Для лучшего понимания влияния темпа роста населения n и темпа технического прогресса g на динамику макроэкономических переменных сведем наш анализ модели роста Солоу в таблицу (рис. 8). Нормой выбытия δ в данном случае мы пренебрегаем, предположив, что срок службы физического капитала составляет весьма значительную величину.

Рис. 8. Влияние темпа роста населения (n) и технического прогресса (g) на динамику макроэкономических показателей; для простоты предположили, что норма выбытия (амортизации) δ = 0

Как видно из таблицы, темп роста выпуска в расчете на единицу эффективного труда в устойчивом состоянии не изменяется; тот же вывод можно сделать относительно показателя капиталовооруженности в расчете на единицу эффективного труда в устойчивом состоянии. Главный же показатель, характеризующий увеличение благосостояние населения, т.е. выпуск на душу населения у растет тем же темпом, что и технический прогресс.

Позвольте еще раз обратить внимание на проблему стационарного, или устойчивого роста в долгосрочном периоде. Когда экономика находится в состоянии устойчивого равновесия в краткосрочном периоде, помимо того, что весь объем сбережений полностью инвестируется, обнаруживается еще одно равенство, связанное с совпадением требуемых и фактически осуществленных валовых инвестиций. Каждому варианту такого равновесия соответствует устойчивый уровень капиталовооруженности k* и равновесный уровень дохода у*. Если мы построим функцию возможных вариантов равновесного дохода в зависимости от всех значений k*, то перед нами предстанет траектория развития экономики в условиях долгосрочного динамического равновесия у* = f(k*), вошедшая в экономическую литературу под названием траектория устойчивого развития.

Так как в модели такой экономики все уровни капиталовооруженности оказываются устойчивыми, то в долгосрочном динамическом равновесии функции требуемых i r и фактических инвестиций sf(k) всегда будут совпадать. Иначе говоря, при любом уровне дохода в условиях динамического равновесия и, соответственно, при всех значениях k* будет сохраняться равенство (n + δ + g)k* = sf(k*).

Итак, модель Солоу показывает, что в долгосрочном периоде рост производства зависит от темпа технического прогресса. Именно этот экзогенный фактор может поддержать непрерывный рост производства, а значит, и рост благосостояния населения, выражающийся в росте выпуска и потребления на душу населения.

[3] Неокейнсианские модели (например, модель Домара) рассматривает прирост инвестиций в качестве единственного фактора роста совокупного спроса и совокупного предложения; см., например, Неокейнсианские модели экономического роста

Источник