Sx vx2 v0x2 2ax что за формула

Sx vx2 v0x2 2ax что за формула

Перемещение

Перемещение тела (материальной точки) – это вектор, соединяющий начальное положение тела с его последующим положением.

Существует большая разница между путем и перемещением. Путь может быть и по прямой, и по извилистой линии, может быть и круговым. Допустим, во всех этих случаях длина пути одинаковая. Очевидно, что расстояние между началом и концом пути будет разным. То есть тело может преодолеть путь длиной в 20 км и при этом переместиться от начальной точки всего на 2 км, на 20 метров или вообще не переместиться (если тело двигалось по кругу, то оно, пройдя круг, вернулось к исходной точке).

Путь – скалярная величина, то есть величина, не имеющая направления.

Перемещение – векторная величина, то есть величина, имеющая направление.

Как и путь, перемещение измеряется в метрах, километрах, сантиметрах и т.д.

Перемещение при прямолинейном равномерном движении.

Формула перемещения для прямолинейного равномерного движения:

→ →
s = v · t

где v – проекция скорости, t – время.

Но для расчета перемещения применяют формулу, в которую входят проекции векторов на ось:

s_x = v_xt

где v_x – проекция скорости, t – время.

Перемещение тела при прямолинейном равноускоренном движении.

Формула 1:

v_0x + v_x
S = ———— · t
2

где t – время, v_0x – проекция начальной скорости, v_x – проекция скорости в конце промежутка времени t.

Формула 2:

Поскольку v_x = v_0x + a_xt, а S = s_x, то формула 1 может иметь и такой вид:

a_xt 2
s_x = v_0xt + ——
2

Перемещение тела при прямолинейном равноускоренном движении без начальной скорости.

Если начальная скорость v₀ равна нулю, то предыдущая формула закономерно обретает следующий вид:

at 2
s = ——
2

Источник

Sx vx2 v0x2 2ax что за формула

Равноускоренным называют движение с постоянным ускорением. Простейшим примером такого движения является свободное падение тел, изучением которых занимался ещё Галилео Галилей. Скорость движения при этом не остаётся постоянной: в общем случае она меняется и по модулю, и по направлению. Описание данного движения значительно сложнее по сравнению с равномерным прямолинейном. Действия с числами здесь заменяют на действия с векторами, так как векторы содержат в себе информацию о направлений величин, характеризующих движение (о скорости, ускорений, перемещений).
Ускорение при равноускоренном движений показывает, на сколько изменяется скорость тела за каждую секунду движения:

(1)

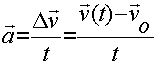
Где V₀ – начальная скорость тела, а V скорость того же тела спустя некоторое время t.
Ускорение показывает изменение скорости за единицу времени.
Из определения ускорения следует, что мгновенная скорость тела при равноускоренном движении изменяется с течением времени по линейному закону:

(2)

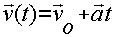
Эта формула позволяет по начальной скорости и ускорению тела вычислить его скорость в любой момент времени t. Между тем основная задача механики заключается в определении того, где будет находиться тело спустя заданное время. Для её решения необходимо знать перемещение, совершённое телом за это время. Перемещение можно найти, умножив среднюю скорость на время движения:

При равноускоренном движении средняя скорость равна полусумме начальной и конечной скоростей движения:

Подставляя сюда выражения (2), получаем:

Именно это уравнение является обобщением формулы:s=vt на случай движения с постоянным ускорением.
Уравнения (1),(2),(3) – векторные. Действия с векторами отличаются от действий с числами, поэтому никакие числовые значения перемещения, скорости и ускорения в такие уравнения подставлять нельзя. Между тем любые расчёты требуют проведений операций именно с числами. Чтобы это стало возможным, необходимо от векторного способа описания движения перейти к координатному. При координатном описаний движения вместо векторов используют проекций на оси координат. Поскольку любой вектор характеризуется тремя проекциями на оси X,Y и Z, следовательно каждому вектору уравнению в общем случае будут соответствовать три уравнения в координатной форме. Для плоского (двухмерного) движения таких уравнений только два. Если же движение является прямолинейным, то для его описания достаточно одного уравнения в проекций на ось X(при условии, что эта ось направлена параллельно вектору скорости частицы). Тогда уравнения (2) и (3).например, можно записать следующим образом:

При координатном описаний движения, координота тела будет равна:

Шелкни мышкой по машине и управлять машиной стрелочками

Источник

Механическое движение

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

Векторные величины (определяются значением и направлением)

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

→ →
V = S/t

→
V — скорость [м/с]
→
S — перемещение [м]
t — время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уравнение движения

Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) = x0 + vxt

x(t) — искомая координата [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

x(t) — искомая координата [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Графики

Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.

В видео ниже разбираемся, как строить графики кинематических величин и зачем они нужны.

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) = x0 + v0xt + axt^2/2

x(t) — искомая координата [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в данный момент времени [м/с]
t — время [с]
ax — ускорение [м/с^2]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

→ →
v = v0 + at

→
v — конечная скорость тела [м/с]
v0 — начальная скорость тела [м/с]
t — время [с]
→
a — ускорение [м/с^2]

Задача

Найдите местоположение автобуса через 0,5 часа после начала движения, разогнавшегося до скорости 60 км/ч за 3 минуты.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, v0 = 0. Значит
a = v/t

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч^2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt^2/2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
x = 1200*0,5^2/2 = 1200*0,522= 150 км

Ответ: через полчаса координата автобуса будет равна 150 км.

Графики

Мы уже знаем, что такое графики функций и зачем они нужны. Для прямолинейного равноускоренного движения графики будут отличаться. Об этом — в видео ниже

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с^2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Источник

Конспект урока «Перемещение при равноускоренном движении.»10 класс

Цель урока: познакомить с графическим способом вывода формулы для перемещения при прямолинейном равноускоренном движении, формировать умение определять перемещение тела с помощью формул.

сформировать понятие перемещения при прямолинейном равноускоренном движении с учётом существования причинно-следственных связей;

рассмотреть графическое представление равноускоренного движения и отработать решение задач на нахождение параметров равноускоренного движения с применением формул;

сформировать практические умения применять знания в конкретных ситуациях.

развивать умение читать и строить графики зависимости перемещения, скорости и ускорения от времени при равноускоренном движении;

развивать речь учащихся через организацию диалогического общения на уроке;

развивать и поддерживать внимание учащихся через смену учебной деятельности.

воспитывать познавательный интерес, любознательность, активность, аккуратность при выполнении заданий, интерес к изучаемому предмету.

Приветствие учащихся. Знакомство с ними. Запись в классный журнал отсутствующих учеников. Сообщение темы урока. Запись ее на доске и в тетрадях учащихся.

Перед тем как мы продолжим изучение данного материала, давайте вспомним и повторим ранее изученное.

Какое движение называют равномерным, прямолинейным?

Что называют скоростью равномерного движения?

В каких единицах измеряют скорость?

Как перевести скорость из км/ч в м/с.

В каких случаях проекция скорости равномерного движения на ось положительна, в каких отрицательна?

Анализ самостоятельной работы.

Проверка домашнего задания

Перемещение при равноускоренном движении

Вспомним основные определения прошлого урока:

— равноускоренным называют такое движение, при котором тело за любые равные промежутки времени изменяет свою скорость на одинаковую величину;

— ускорением называют отношение изменения скорости тела ко времени, за которое это изменение произошло;

— закон изменения скорости от времени и проекции скорости от времени для равноускоренного движения:

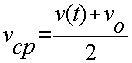
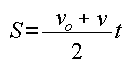
(t) = + t

(t) = V _0x + a _x t

Если мы знаем закон, по которому меняется скорость со временем либо проекция скорости со временем при равноускоренном движении, как же нам получить закон, по которому меняется проекция перемещения со временем? Для этого вспомним, какой вид имеет график зависимости проекции скорости от времени при равноускоренном и равномерном движении (Рис. 1):

Рис. 1. Графики зависимости скорости от времени при равноускоренном и равномерном прямолинейном движениях

При равноускоренном движении график имеет вид прямой линии, уходящей вверх, так как его проекция ускорения больше нуля.

При равномерном прямолинейном движении площадь численно будет равна модулю проекции перемещения тела. Оказывается, этот факт можно обобщить для случая не только равномерного движения, но и для любого движения, то есть показать, что площадь под графиком численно равна модулю проекции перемещения. Это делается строго математически, но мы воспользуемся графическим способом.

Рис. 2. График зависимости скорости от времени при равноускоренном движении

Разобьем график проекции скорости от времени для равноускоренного движения на небольшие промежутки времени Δt. Предположим, что они так малы, что на их протяжении скорость практически не менялась, то есть график линейной зависимости на рисунке мы условно превратим в лесенку. На каждой ее ступеньке мы считаем, что скорость практически не поменялась. Представим, что промежутки времени Δt мы сделаем бесконечно малыми. В математике говорят: совершаем предельный переход. В этом случае площадь такой лесенки будет неограниченно близко совпадать с площадью трапеции, которую ограничивает график V _x (t). А это значит, что и для случая равноускоренного движения можно сказать, что модуль проекции перемещения численно равен площади, ограниченной графиком V _x (t): осями абсцисс и ординат и перпендикуляром, опущенным на ось абсцисс, то есть площади трапеции ОАВС, которую мы видим на рисунке 2.

Задача из физической превращается в математическую задачу – поиск площади трапеции. Это стандартная ситуация, когда ученые физики составляют модель, которая описывает то или иное явление, а затем в дело вступает математика, которая обогащает эту модель уравнениями, законами – тем, что превращает модель в теорию.

Рис. 3. Определение площади трапеции

Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, получим:

Мы с вами получили закон зависимости проекции перемещения от времени при равноускоренном движении в скалярной форме, в векторной форме он будет выглядеть так:

(t) = t + t 2 / 2

Уравнение координаты. Примеры

Выведем еще одну формулу для проекции перемещения, в которую не будет входить в качестве переменной время. Решим систему уравнений, исключив из нее время:

Представим, что время нам неизвестно, тогда выразим время из второго уравнения:

Подставим полученное значение в первое уравнение:

Получим такое громоздкое выражение, возведем в квадрат и приведем подобные:

Мы получили очень удобное выражение проекции перемещения для случая, когда нам неизвестно время движения.

Проанализируем следующую формулу:

Проекция перемещения– это полусумма проекций начальной и конечной скоростей, умноженная на время движения. Вспомним формулу перемещения для средней скорости

В случае равноускоренного движения средняя скорость будет:

Мы вплотную подошли к решению главной задачи механики равноускоренного движения, то есть получению закона, по которому меняется координата со временем:

Для того чтобы научиться пользоваться этим законом, разберем типичную задачу.

Лыжник съезжает со склона горы из состояния покоя с ускорением 0,5 м/с 2 за 20 с и дальше движется по горизонтальному участку, проехав до остановки 40 м. С каким ускорением двигался лыжник по горизонтальной поверхности? Какова длина склона горы?

Движение лыжника состоит из двух этапов: на первом этапе, спускаясь со склона горы, лыжник движется с возрастающей по модулю скоростью; на втором этапе при движении по горизонтальной поверхности его скорость уменьшается. Величины, относящиеся к первому этапу движения, запишем с индексом 1, а ко второму этапу с индексом 2.

Систему отсчета свяжем с Землей, ось X направим по направлению скорости лыжника на каждом этапе его движения Запишем уравнение для скорости лыжника в конце спуска с горы:

Запишем уравнение, связывающее проекции скорости, ускорения и перемещения лыжника на втором этапе движения:

Учитывая, что начальная скорость лыжника на этом этапе движения равна его конечной скорости на первом этапе

Модуль перемещения лыжника на первом этапе движения равен длине склона горы. Запишем уравнение для перемещения:

Отсюда длина склона горы равна s ₁ = ;

Источник

• ← Sx vx 2 v0x 2 2ax что за формула
• Sx4 или vitara что лучше →