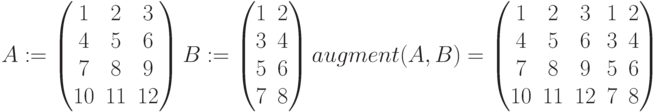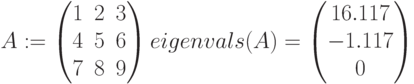Submatrix mathcad что это
Submatrix mathcad что это
Найдем определитель, используя кнопку Determinant в панели Matrix or Vector Toolbar:
Для нахождения определителя матриц M11, M12, M13, M14 воспользуйтесь нопкой Determinant в панели Matrix or Vector Toolbar.
Формула вычисления определителя разложением по 1-ой строке:
Функция submatrix(A, 2, 4, 2, 4) формирует матрицу третьего порядка M11, содержащую элементы 2-4-ой строк 2-4-го столбцов матрицы А, т.е. матрицу, полученную вычеркиванием 1-ой строки и 1-го столбца;
функция augment(submatrix(A, 2, 4, 1, 1), submatrix(A,m 2, 4, 3, 4)) формирует матрицу третьего порядка M12, полученную вычеркиванием 1-ой строки и 2-го столбца: к блоку, содержащему элементы 2-4-ой строк 1-го столбца матрицы A, дописываем справа элементы 2-4-ой строк 3-го и 4-го столбцов матрицы A.
Аналогично формируются матрицы M13 и M14.
Сформируем матрицы M11, M12, M13, M14 третьего порядка (полученные вычеркиванием 1-ой строки и соответственно 1-, 2-, 3-, 4-го столбцов матрицы А ) с использованием функций submatrix и augment Mathcad:
Определим матрицу A:
Чтобы столбцы и строки матрицы нумеровались, начиная с единицы, присвойте переменной ORIGIN значение, равное единице.
Знак присваивания можно ввести щелчком по соответствующей позиции в панели Evaluation Toolbar панели математических инструментов.
Вычислим определитель матрицы четвертого порядка разложением по 1-ой строке
Submatrix mathcad что это
Mathcad для студентов
Mathcad для начинающих
Скачать программы бесплатно
Матричные функции в Mathcad
Mathсad имеет более 50 функций, предназначенных для работы с векторами и матрицами. Все функции можно разбить на группы по их функциональному назначению. Например, функции, предназначенные для создания матриц общего и специального вида, редактирования и преобразования матриц, функции, определяющие параметры матриц и т. д. Рассмотрим часть этих функций, которые имеют наибольшее прикладное значение.
Для определения размерности матрицы в Mathcad предназначены функция rows(M), определяющая число строк матрицы M, и функция cols(M), определяющая число колонок матрицы M.
Сортировку элементов матрицы осуществляют две функции csort(M,i), rsort(M,j). Функция csort(M,i) обеспечивает сортировку по возрастанию элементов i – го столбца путем перестановки строк, а функция rsort(M,j) – сортировку по возрастанию элементов j –ой строки путем перестановки столбцов.
Для определения минимального и максимального элемента матрицы используются функции min(M) и max(M).
Выделить произвольную подматрицу из матрицы М в Mathcad можно посредством функции submatrix (M, r1, r2, c1, c2), где М – исходная матрица, r1 и r2 –нижний и верхний номер строки матрицы М, включаемых в результирующую подматрицу, а с1 и с2 – нижней и верхний номер столбца матрицы М, включаемых в результирующую подматрицу. Слияние матриц можно осуществить, используя функции augment(A,B,…) и stack(A,B,…). Функция augment(A,B,…) предназначена для слияния матриц А, В и т.д. слева направо. Причем количество строк в матрицах должно быть одинаково. Вторая функция stack(A,B,…) выполняет слияние матриц сверху вниз. Количество столбцов в матрицах должно быть также одинаково. Данные функции могут быть применены и к векторам. На листинге приведен пример использования рассмотренных матричных функций.
Submatrix mathcad что это
Mathcad для студентов
Mathcad для начинающих
Скачать программы бесплатно
Матричные функции в Mathcad
Mathсad имеет более 50 функций, предназначенных для работы с векторами и матрицами. Все функции можно разбить на группы по их функциональному назначению. Например, функции, предназначенные для создания матриц общего и специального вида, редактирования и преобразования матриц, функции, определяющие параметры матриц и т. д. Рассмотрим часть этих функций, которые имеют наибольшее прикладное значение.
Для определения размерности матрицы в Mathcad предназначены функция rows(M), определяющая число строк матрицы M, и функция cols(M), определяющая число колонок матрицы M.
Сортировку элементов матрицы осуществляют две функции csort(M,i), rsort(M,j). Функция csort(M,i) обеспечивает сортировку по возрастанию элементов i – го столбца путем перестановки строк, а функция rsort(M,j) – сортировку по возрастанию элементов j –ой строки путем перестановки столбцов.
Для определения минимального и максимального элемента матрицы используются функции min(M) и max(M).
Выделить произвольную подматрицу из матрицы М в Mathcad можно посредством функции submatrix (M, r1, r2, c1, c2), где М – исходная матрица, r1 и r2 –нижний и верхний номер строки матрицы М, включаемых в результирующую подматрицу, а с1 и с2 – нижней и верхний номер столбца матрицы М, включаемых в результирующую подматрицу. Слияние матриц можно осуществить, используя функции augment(A,B,…) и stack(A,B,…). Функция augment(A,B,…) предназначена для слияния матриц А, В и т.д. слева направо. Причем количество строк в матрицах должно быть одинаково. Вторая функция stack(A,B,…) выполняет слияние матриц сверху вниз. Количество столбцов в матрицах должно быть также одинаково. Данные функции могут быть применены и к векторам. На листинге приведен пример использования рассмотренных матричных функций.
Встроенные функции MathCAD
Часто используемые функции
ceil(y) – возвращает наименьшее целое, большее или равное y. Значение y должно быть вещественным числом:
cols(A) – число столбцов матрицы А.
csort(B,n) – сортирует строки матрицы В таким образом, чтобы расположить элементы столбца n в порядке возрастания. Нумерация столбцов по умолчанию начинается с нуля:
eigenvals(A) – определяет вектор собственных значений для квадратной матрицы А:
find(x,y,…) – возвращает значения x,y,…, удовлетворяющие ограничениям: равенствам или неравенствам, заданным в блоке given решения уравнений. Число уравнений должно равняться числу неизвестных.
floor(y) – возвращает наибольшее целое, меньшее или равное y. Значение y должно быть вещественным числом:
identity(n) – создает единичную матрицу размером
length(v) – длина вектора v.
max(v) – максимальный по значению элемент вектора v.
min(v) – минимальный по значению элемент вектора v.
mean(M) – среднее арифметическое элементов вектора или матрицы.
median(v) – медиана вектора. Элементы вектора должны быть заданы в порядке возрастания:
rbeta (m, s 1, s2)Возвращает вектор m случайных чисел, имеющих бэта-распределение. 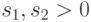
rgamma (m, s) Возвращает вектор m случайных чисел, имеющих гамма- распределение, 
rgeom (m, p) Возвращает вектор m случайных чисел, имеющих геометрическое распределение. 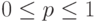
rlogis (m, l, s) Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а 
rpois (m,d) Возвращает вектор m случайных чисел, имеющих распределение Пуассона. 
rt (m, d) Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента. 
runif (m, a, b) Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. 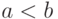
rnd (x) Возвращает равномерно распределенное случайное число между 0 и x. Эквивалент runif (1, 0, x).
round(y,n) – округляет вещественное число y до n знаков справа от десятичной точки. Если n отсутствует, то y округляется до ближайшего целого числа. Если n Нумерация строк по умолчанию начинается с нуля.
submatrix(M,ir,jr,ic,jc) – подматрица, состоящая из элементов матрицы М, содержащихся в строках от ir до jr и столбцах от ic до jc:
Submatrix mathcad что это
Mathcad для студентов
Mathcad для начинающих
Скачать программы бесплатно
Решение системы линейных алгебраических уравнений матричным способом в Mathcad
Решение системы линейных алгебраических уравнений методом Крамера в Mathcad
В Mathcad метод Крамера также предназначен для решения системы n линейных уравнений с n неизвестными вида A*x =b на основе предварительного вычисления определителей системы, при условии, что определитель 


Матрицы и векторы в Mathcad
Наиболее удобно выполнять матричные вычисления с использованием кнопок панели инструментов “Матрица”. По умолчанию индексация строк и столбцов элементов матрицы начинается с 0. Для того чтобы индексация начиналась с 1, необходимо системной переменной ORIGIN присвоить значение 1. На листинге приведен пример матричных вычислений в Mathсad.
Матричные функции в Mathcad
Mathсad имеет более 50 функций, предназначенных для работы с векторами и матрицами. Все функции можно разбить на группы по их функциональному назначению. Например, функции, предназначенные для создания матриц общего и специального вида, редактирования и преобразования матриц, функции, определяющие параметры матриц и т. д. Рассмотрим часть этих функций, которые имеют наибольшее прикладное значение.
Для определения размерности матрицы в Mathcad предназначены функция rows(M), определяющая число строк матрицы M, и функция cols(M), определяющая число колонок матрицы M.
Сортировку элементов матрицы осуществляют две функции csort(M,i), rsort(M,j). Функция csort(M,i) обеспечивает сортировку по возрастанию элементов i – го столбца путем перестановки строк, а функция rsort(M,j) – сортировку по возрастанию элементов j –ой строки путем перестановки столбцов.
Для определения минимального и максимального элемента матрицы используются функции min(M) и max(M).
Выделить произвольную подматрицу из матрицы М в Mathcad можно посредством функции submatrix (M, r1, r2, c1, c2), где М – исходная матрица, r1 и r2 –нижний и верхний номер строки матрицы М, включаемых в результирующую подматрицу, а с1 и с2 – нижней и верхний номер столбца матрицы М, включаемых в результирующую подматрицу. Слияние матриц можно осуществить, используя функции augment(A,B,…) и stack(A,B,…). Функция augment(A,B,…) предназначена для слияния матриц А, В и т.д. слева направо. Причем количество строк в матрицах должно быть одинаково. Вторая функция stack(A,B,…) выполняет слияние матриц сверху вниз. Количество столбцов в матрицах должно быть также одинаково. Данные функции могут быть применены и к векторам. На листинге приведен пример использования рассмотренных матричных функций.
Матричные вычисления в Mathcad
Создание векторов и матриц реализовано в Mathсad различными способами. В данном разделе рассматриваются только функции и операции с векторами и матрицами, а так же прикладное использование векторов и матриц для решения некоторых задач.
Матричные функции
В Mathсad очень много функций, предназначенных для работы с матрицами и векторами.
Основные операции с матрицами и векторами
Операции, выполняемые над векторами и матрицами, можно разбить на разные большие группы.
Решение системы линейных алгебраических уравнений матричным способом
В Mathcad можно решать системы линейных алгебраических уравнений матричным способом.
Решение системы линейных алгебраических уравнений методом Крамера
Также предназначен метод Крамера для решения системы n линейных уравнений с n неизвестными.