способы обучения нейронных сетей

Обучение нейронной сети

Обучение нейронной сети— это процесс, в котором параметры нейронной сети настраиваются посредством моделирования среды, в которую эта сеть встроена. Тип обучения определяется способом подстройки параметров. Различают алгоритмы обучения с учителем и без учителя.
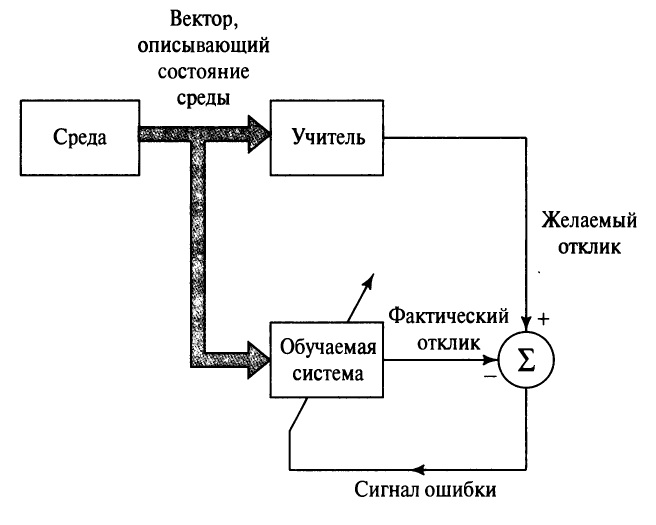
Процесс обучения с учителем представляет собой предъявление сети выборки обучающих примеров. Каждый образец подается на входы сети, затем проходит обработку внутри структуры НС, вычисляется выходной сигнал сети, который сравнивается с соответствующим значением целевого вектора, представляющего собой требуемый выход сети.

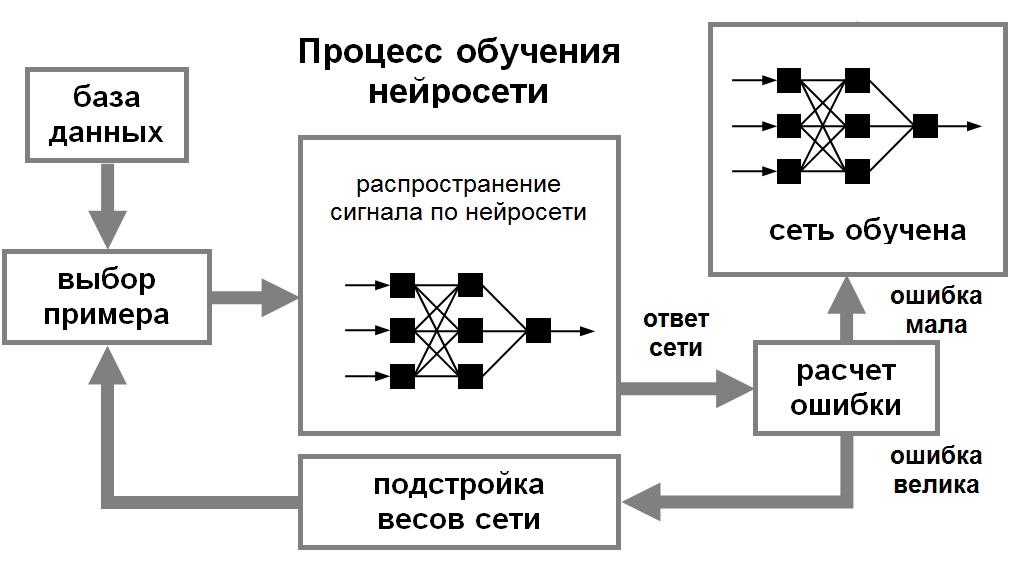
Для того, чтобы нейронная сети была способна выполнить поставленную задачу, ее необходимо обучить (см. рис. 1). Различают алгоритмы обучения с учителем и без учителя.
Процесс обучения с учителем представляет собой предъявление сети выборки обучающих примеров. Каждый образец подается на входы сети, затем проходит обработку внутри структуры НС, вычисляется выходной сигнал сети, который сравнивается с соответствующим значением целевого вектора, представляющего собой требуемый выход сети. Затем по определенному правилу вычисляется ошибка, и происходит изменение весовых коэффициентов связей внутри сети в зависимости от выбранного алгоритма. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.

Рис. 1. Иллюстрация процесса обучения НС

При обучении без учителя обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т.е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью.
Для обучения нейронных сетей без учителя применяются сигнальные метод обучения Хебба и Ойа.

Математически процесс обучения можно описать следующим образом. В процессе функционирования нейронная сеть формирует выходной сигнал Y, реализуя некоторую функцию Y = G(X). Если архитектура сети задана, то вид функции G определяется значениями синаптических весов и смещенной сети.

Обучение состоит в поиске (синтезе) функции G, близкой к F в смысле некторой функции ошибки E. (см. рис. 1.8).

Для решения этой задачи могут использоваться следующие (итерационные) алгоритмы:

алгоритмы локальной оптимизации с вычислением частных производных первого порядка:

градиентный алгоритм (метод наискорейшего спуска),

методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента,

метод сопряженных градиентов,

методы, учитывающие направление антиградиента на нескольких шагах алгоритма;

алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядка:

методы оптимизации с разреженными матрицами Гессе,

метод Левенберга-Марквардта и др.;

стохастические алгоритмы оптимизации:

поиск в случайном направлении,

метод Монте-Карло (численный метод статистических испытаний);

алгоритмы глобальной оптимизации (задачи глобальной оптимизации решаются с помощью перебора значений переменных, от которых зависит целевая функция).

Источник

Методы обучения нейронных сетей

Содержание

Каждая созданная нейронная сеть требует обучения, в противном случае правильный результат вряд ли будет получен. Методов обучения нейросети существует несколько.

Тем не менее среди них выделяют три наиболее интересных способов, это методы обратного и упругого распространения, а также генетический анализ. О них и поговорим более подробно.

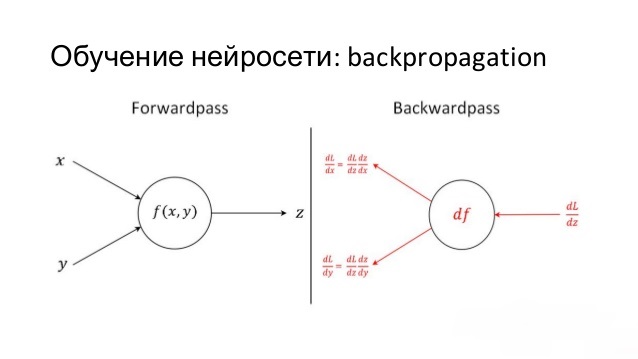
Метод обратного распространения

Этот метод является основным и имеет ещё одно название — Backpropagation, так как использует алгоритм градиентного спуска. То есть при помощи движения вдоль градиента рассчитывается локальный минимум и максимум функции. Понимание этого метода приведёт к тому, что следующий не вызовет затруднений.

Если представить функцию в виде графика, определяющего зависимость ошибки от веса синапса, то на этом графике необходимо найти точку с минимальным значением ошибки и с максимальным. При этом каждый вес должен иметь своё графическое представление и к каждому из них необходимо вычислить глобальный минимум.

Сам градиент представляет собой векторное значение определяющее направление и крутизну склона. Градиент находится с помощью производной от функции в нужной точке. Оказавшись в определённой точке со значением веса, который распределяется в случайном порядке, вычисляется градиент и определяется направление движения спуска, и так в каждой следующей точке, пока не достигается локальный минимум, не позволяющий дальнейшего спуска.

Чтобы справиться с этой неприятностью необходимо установить нужное значение момента, которое позволит преодолеть часть графика и достигнуть нужной точки. Если это значение будет недостаточным, то преодолеть выпуклость не получится, в случае с установкой более высокого значения, чем нужно есть шансы проскочить глобальный минимум.

Кроме момента ускорения, есть ещё понятие, определяющее общую скорость обучения сети. Это значение, как и предыдущее представляет собой гиперпараметр и подбирается методом проб и ошибок. Оптимальный вариант заранее никогда не известен, узнать его можно только проведя несколько обучений и корректируя каждый раз значение в нужном направлении.

Теперь можно перейти непосредственно к методу обучения и определить, что он из себя представляет. В процессе поступления информации нейронная сеть последовательно передаёт её от одного нейрона к другому посредством синапсов, до того момента, пока информация не окажется на выходном слое и не будет выдана как результат. Такой способ называется передачей вперёд.

После того как результат получен вычисляется ошибка и на её сновании выполняем обратную передачу. Суть которой — последовательно изменить вес синапсов начиная с выходного и продвигаясь к входному слою. При этом значение веса меняется в сторону лучшего результата.

Для использования такого метода обучения подойдут только те функции активации, которые можно дифференцировать. Так как обратное распространение вычисляется с помощью высчитывания разницы результатов и умножения его на производную функции от входного значения.

Для того чтобы успешно провести обучение, необходимо распространить полученную ошибку на весь вес сети. Высчитав ошибку на выходном уровне, а также там можно вычислить дельту, которая будет последовательно передаваться между нейронами.

Затем необходимо произвести расчёт градиента для каждой исходящей связи. Затем имея все необходимые данные необходимо выполнить обновление весов и рассчитать благодаря функции МОР значение, которое станет величиной изменения.

При этом не стоит забывать про момент и скорость обучения.

Одна итерация МОР даёт небольшой процент уменьшения ошибки, поэтому повторять их необходимо снова и снова пока показатель ошибки не будет приближен к 0.

Метод упругого распространения

Следующий метод обучения сети Resilient propagation или Rprop. Предыдущий способ обучения, представленный выше имеет недостаток в виде больших временных затрат на процесс обучения неуместных в случае необходимости получить быстрый результат.

Для ускорения процесса было предложено немало дополнительных алгоритмов, ускоряющих процесс. Одним из которых и является текущий метод.

Настоящий алгоритм использует в качестве основы обучение по эпохам и применяет только знаки производных частного случая для корректировки весовых коэффициентов. Используется определённое правило, по которому производится расчёт величины коррекции весового коэффициента.

Если на этом этапе расчётов производная меняет свой знак, значит, изменение было слишком большим и локальный минимум был упущен и нужно произвести откат, то есть вес вернуть в обратную позицию, а величину изменения уменьшить.

Если знак производной не изменился, то величина изменения веса, наоборот, увеличивается для большей сходимости.

Если основные параметры коррекции веса зафиксировать, то настройки глобальных параметров можно избежать. И это станет ещё одним преимуществом текущего метода над предыдущим. Для этих параметров есть рекомендуемые значения, однако, никаких ограничений на их выбор не накладывается.

Чтобы вес не принимал слишком большие или малые значения используются установленные ограничения величины коррекции. Значение коррекции также вычисляется по определённому правилу.

Уважаемые посетители, сохраните эту статью в социальных сетях. Мы публикуем очень полезные статьи, которые помогут Вам в вашем деле. Поделитесь! Жмите!

То есть если производная функции в конкретной точке меняет знак с плюса на минус, означает, что ошибка возрастает и вес требует коррекции и происходит его уменьшение, в противном случае — увеличение.

Последовательность действий в этом случае следующая: инициализируется величина коррекции, вычисляются частные производные, подсчитывается новое значение коррекции значений весов, корректируются веса, если условие остановки алгоритма не выполняются процесс переходит к вычислению производных и заново повторяет цикл. Такой подход позволяет добиться сходимости нейросети быстрее в несколько раз в отличие от предыдущего варианта обучения.

Генетический Алгоритм

Третий наиболее интересный алгоритм обучения искусственных нейронных сетей — Genetic Algorithm. Он представляет собой упрощённую интерпретацию природного алгоритма, основанного на скрещивании результатов. То есть, по сути, происходит скрещивание результатов, выбор наилучших и формирование на их основе нового поколения.

В случае если результат не устраивает алгоритм повторяется пока поколение не становиться идеальным. Алгоритм может завершиться без достижения нужного результата если количество попыток будет исчерпано или же будет исчерпан время на мутацию. Этот алгоритм применим к процессу оптимизации веса нейронной сети, при заданной по умолчанию топологии.

При этом вес кодируется двоичным кодом и каждый результат определяется полным набором веса. Оценка качества происходит методом вычисления ошибки на выходе.

Видеомаркетинг поможет привлечь клиентов и продвинуть ваш товар.

Как правильно заполнить сниппет, читай в нашей статье.

Рекомендации по написанию хорошей статьи ты найдешь здесь.

Другие вариации обучения

Кроме вышеперечисленных методов, есть ещё разновидности обучения нейросетей с учителем и без него. Обучение с учителем чаще всего применимо к регрессиям и классификациям.

В этом случае тренер выступает в роли учителя, а созданная сеть — ученика. Тренер задаёт входные данные и требующийся результат, соответственно сеть понимает к какому именно результату необходимо стремиться при заданных параметрах.

Обучение без учителя носит несколько иной характер и встречается реже. При таком раскладе нейронная сеть не получает желаемого результата. Такая тренировка подходит сетям, задача которых кластеризация данных по заданным параметрам. То есть, проанализировав большой объем входных данных, сеть разделяет их на категории по определённым признакам.

Обучение с подкреплением применяется тогда, когда есть возможность оценить итоговый результат, выданный сетью.

То есть путём определённого поощрения нейронной сети каждый раз, когда полученный результат максимально приближен к желаемому мы дадим ей возможность искать любые пути решения проблемы, пока она будет давать нужные результаты.

Благодаря этому сеть будет искать наилучшие способы достижения цели без данных от тренера.

Есть ещё несколько методов обучения:

В процессе любого обучения приходится применять гиперпараметры, подбор которых выполняется вручную, при этом они не являются переменными в определённом уравнении. Это уже упомянутые выше момент и скорость обучения.

Также к этим параметрам можно отнести количество скрытых слоёв, число нейронов в слое, присутствие нейронов смещения или, наоборот, их отсутствие. Наличие гиперпараметров в первую очередь определяется типом искусственной нейронной сети. Правильный подбор их значений напрямую влияет на сходимость сети.

В случае когда процесс обучения затягивается есть риск возникновения ситуации, в которой потребуется переобучение сети. Как правило, это происходит в момент, когда сеть перенасыщена данными и начинает не обучаться, а просто запоминать результаты для определённого набора входных параметров. И при подаче новых параметров возникают шумы, влияющие на результат.

Чтобы избежать такой необходимости, обучение необходимо проводить на разных входных данных имеющих значительные различия между собой.

Нейронные сети — очень перспективное направление разработки. Создав нейронную сеть можно обучить её многому, в частности тому, что человек привык делать бессознательно, а соответственно алгоритм чего ему неизвестен.

Считается, что нейросети являются аналогом человеческого мозга, возможно, это и так, но стоит помнить — это всего лишь копия, отдалённо напоминающая свой прототип.

Источник

Обучение нейросети с учителем, без учителя, с подкреплением — в чем отличие? Какой алгоритм лучше?

Обучить нейронную сеть можно разными способами: с учителем, без учителя, с подкреплением. Но как выбрать оптимальный алгоритм и чем они отличаются? Есть несколько способов собрать мебель из IKEA. Каждый из них приводит к собранному дивану или стулу. Но в зависимости от предмета мебели и его составляющих один способ будет более разумным, чем другие.

Есть руководство по эксплуатации и все нужные детали? Просто следуйте инструкции. Ну как, получается? Можно выбросить руководство и работать самостоятельно. Но стоит перепутать порядок действий, и уже вам решать, что делать с этой кучей деревянных болтов и досок.

Все то же самое с глубоким обучением (deep learning). Разработчик предпочтет алгоритм с конкретным способом обучения, учитывая вид данных и стоящую перед ним задачу.

Результат обучения нейронной сети — кластеризация изображений

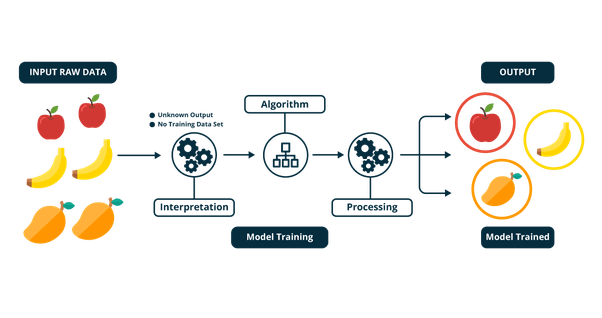
При обучении с учителем нейронная сеть обучается на размеченном наборе данных и предсказывает ответы, которые используются для оценки точности алгоритма на обучающих данных. При обучении без учителя модель использует неразмеченные данные, из которых алгоритм самостоятельно пытается извлечь признаки и зависимости.

Обучение с частичным привлечением учителя представляет собой нечто среднее. Оно использует небольшое количество размеченных данных и большой набор неразмеченных. А обучение с подкреплением тренирует алгоритм при помощи системы поощрений. Агент получает обратную связь в виде вознаграждений за правильные действия. Похожим образом дрeссируют животных.

Для каждого способа обучения рассмотрим примеры подходящих для него данных и задач.

Обучение с учителем

Обучение с учителем (supervised learning) предполагает наличие полного набора размеченных данных для тренировки модели на всех этапах ее построения.

Наличие полностью размеченного датасета означает, что каждому примеру в обучающем наборе соответствует ответ, который алгоритм и должен получить. Таким образом, размеченный датасет из фотографий цветов обучит нейронную сеть, где изображены розы, ромашки или нарциссы. Когда сеть получит новое фото, она сравнит его с примерами из обучающего датасета, чтобы предсказать ответ.

Пример обучения с учителем — классификация (слева), и дальнейшее ее использование для сегментации и распознавания объектов

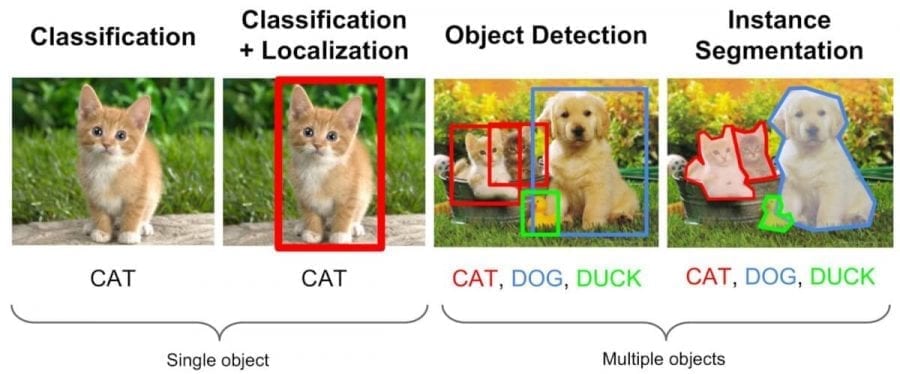
В основном обучение с учителем применяется для решения двух типов задач: классификации и регрессии.

В задачах классификации алгоритм предсказывает дискретные значения, соответствующие номерам классов, к которым принадлежат объекты. В обучающем датасете с фотографиями животных каждое изображение будет иметь соответствующую метку — «кошка», «коала» или «черепаха». Качество алгоритма оценивается тем, насколько точно он может правильно классифицировать новые фото с коалами и черепахами.

А вот задачи регрессии связаны с непрерывными данными. Один из примеров, линейная регрессия, вычисляет ожидаемое значение переменной y, учитывая конкретные значения x.

Более утилитарные задачи машинного обучения задействуют большое число переменных. Как пример, нейронная сеть, предсказывающая цену квартиры в Сан-Франциско на основе ее площади, местоположения и доступности общественного транспорта. Алгоритм выполняет работу эксперта, который рассчитывает цену квартиры исходя из тех же данных.

Таким образом, обучение с учителем больше всего подходит для задач, когда имеется внушительный набор достоверных данных для обучения алгоритма. Но так бывает далеко не всегда. Недостаток данных — наиболее часто встречающаяся проблема в машинном обучении на 2018 год.

Обучение без учителя

Идеально размеченные и чистые данные достать нелегко. Поэтому иногда перед алгоритмом стоит задача найти заранее не известные ответы. Вот где нужно обучение без учителя.

В обучении без учителя (unsupervised learning) у модели есть набор данных, и нет явных указаний, что с ним делать. Нейронная сеть пытается самостоятельно найти корелляции в данных, извлекая полезные признаки и анализируя их.

Кластеризация данных на основе общих признаков

В зависимости от задачи модель систематизирует данные по-разному.

В обучении без учителя сложно вычислить точность алгоритма, так как в данных отсутствуют «правильные ответы» или метки. Но размеченные данные часто ненадежные или их слишком дорого получить. В таких случаях, предоставляя модели свободу действий для поиска зависимостей, можно получить хорошие результаты.

Обучение с частичным привлечением учителя

Это золотая середина.

Обучение с частичным привлечением учителя (semi-supervised learning) характеризуется своим названием: обучающий датасет содержит как размеченные, так и неразмеченные данные. Этот метод особенно полезен, когда трудно извлечь из данных важные признаки или разметить все объекты – трудоемкая задача.

Обучение с частичным привлечением учителя часто используют для решения медицинских задач, где небольшое количество размеченных данных может привести к значительному повышению точности

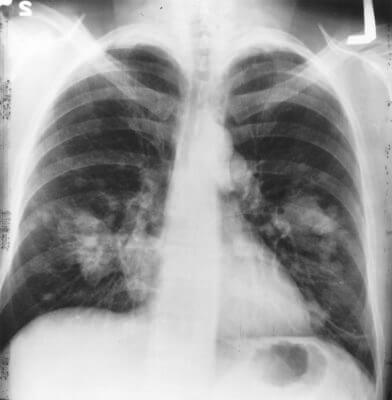
Этот метод машинного обучения распространен для анализа медицинских изображений, таких как сканы компьютерной томографии или МРТ. Опытный рентгенолог может разметить небольшое подмножество сканов, на которых выявлены опухоли и заболевания. Но вручную размечать все сканы — слишком трудоемкая и дорогостоящая задача. Тем не менее нейронная сеть может извлечь информацию из небольшой доли размеченных данных и улучшить точность предсказаний по сравнению с моделью, обучающейся исключительно на неразмеченных данных.

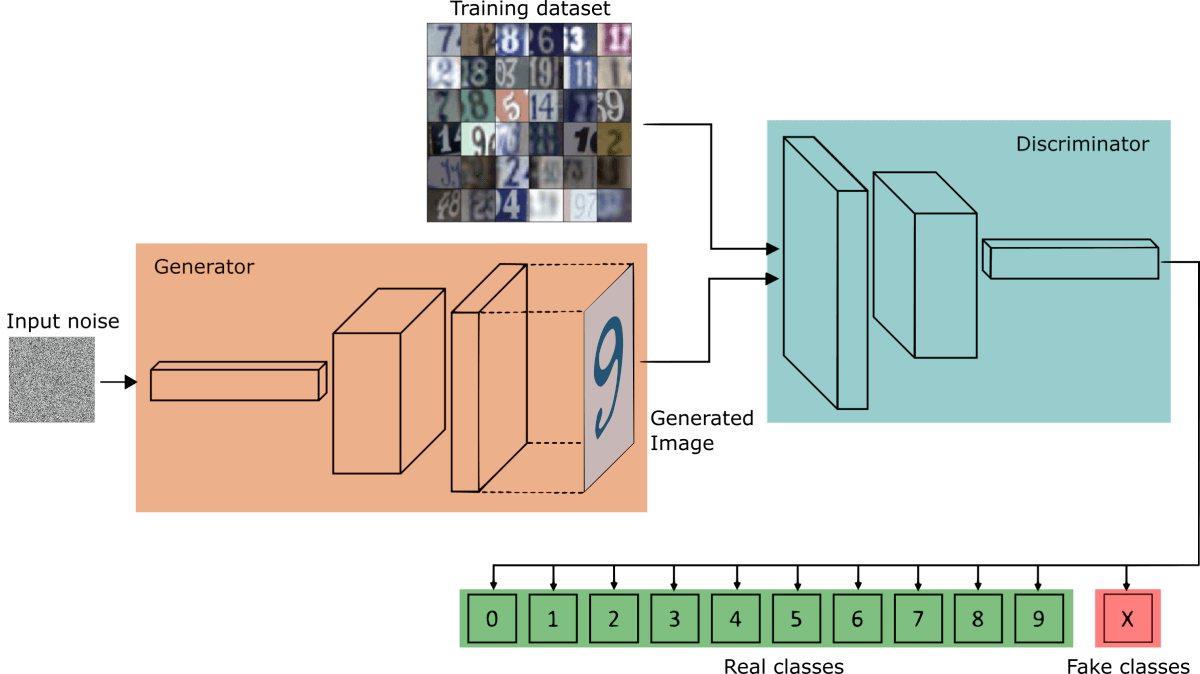
Популярный метод обучения, для которого требуется небольшой набор размеченных данных, заключается в использовании генеративно-состязательной сети или GAN.

Представьте себе соревнование двух нейронных сетей, где каждая пытается перехитрить другую. Это GAN. Одна из сетей, генератор, пытается создать новые объекты данных, которые имитируют обучающую выборку. Другая сеть, дискриминатор, оценивает, являются ли эти сгенерированные данные реальными или поддельными. Сети взаимодействуют и циклично совершенствуются, поскольку дискриминатор старается лучше отделять подделки от оригиналов, а генератор пытается создавать убедительные подделки.

Как работает GAN: дискриминатору «D» показывают исходные изображения и данные, созданные генератором «G». Дискриминатор должен определить, какие изображения являются реальными, а какие поддельными.

Обучение с подкреплением

Видеоигры основаны на системе стимулов. Завершите уровень и получите награду. Победите всех монстров и заработаете бонус. Попали в ловушку – конец игры, не попадайте. Эти стимулы помогают игрокам понять, как лучше действовать в следующем раунде игры. Без обратной связи люди бы просто принимали случайные решения и надеялись перейти на следующий игровой уровень.

Обучение с подкреплением (reinforcement learning) действует по тому же принципу. Видеоигры — популярная тестовая среда для исследований.

Результат обучения с подкреплением — «агент» проходит трассу, не выезжая за ее пределы. Далее можно добивиться повышения скорости прохождения трассы.

Агенты ИИ пытаются найти оптимальный способ достижения цели или улучшения производительности для конкретной среды. Когда агент предпринимает действия, способствующие достижению цели, он получает награду. Глобальная цель — предсказывать следующие шаги, чтобы заработать максимальную награду в конечном итоге.

При принятии решения агент изучает обратную связь, новые тактики и решения способные привести к большему выигрышу. Этот подход использует долгосрочную стратегию — так же как в шахматах: следующий наилучший ход может не помочь выиграть в конечном счете. Поэтому агент пытается максимизировать суммарную награду.

Это итеративный процесс. Чем больше уровней с обратной связи, тем лучше становится стратегия агента. Такой подход особенно полезен для обучения роботов, которые управляют автономными транспортными средствами или инвентарем на складе.

Так же, как и ученики в школе, каждый алгоритм учится по-разному. Но благодаря разнообразию доступных методов, вопрос в том, чтобы выбрать подходящий и научить вашу нейронную сеть разбираться в среде.

Источник

Нейронные сети для начинающих. Часть 2

Добро пожаловать во вторую часть руководства по нейронным сетям. Сразу хочу принести извинения всем кто ждал вторую часть намного раньше. По определенным причинам мне пришлось отложить ее написание. На самом деле я не ожидал, что у первой статьи будет такой спрос и что так много людей заинтересует данная тема. Взяв во внимание ваши комментарии, я постараюсь предоставить вам как можно больше информации и в то же время сохранить максимально понятный способ ее изложения. В данной статье, я буду рассказывать о способах обучения/тренировки нейросетей (в частности метод обратного распространения) и если вы, по каким-либо причинам, еще не прочитали первую часть, настоятельно рекомендую начать с нее. В процессе написания этой статьи, я хотел также рассказать о других видах нейросетей и методах тренировки, однако, начав писать про них, я понял что это пойдет вразрез с моим методом изложения. Я понимаю, что вам не терпится получить как можно больше информации, однако эти темы очень обширны и требуют детального анализа, а моей основной задачей является не написать очередную статью с поверхностным объяснением, а донести до вас каждый аспект затронутой темы и сделать статью максимально легкой в освоении. Спешу расстроить любителей “покодить”, так как я все еще не буду прибегать к использованию языка программирования и буду объяснять все “на пальцах”. Достаточно вступления, давайте теперь продолжим изучение нейросетей.

Что такое нейрон смещения?

Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь.

Для чего нужен нейрон смещения?

Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу H1, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.

Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес H1, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.

Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.

ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:

input = H1*w1+H2*w2+b3
b3 = bias*w3

Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.

Как сделать чтобы НС давала правильные ответы?

Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:

Что такое градиентный спуск?

Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e).

Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.

Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:

Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:

Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?

Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже).

Что такое Метод Обратного Распространения (МОР)?

А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).

Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.

H1input = 1*0.45+0*-0.12=0.45
H1output = sigmoid(0.45)=0.61

H2input = 1*0.78+0*0.13=0.78
H2output = sigmoid(0.78)=0.69

O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33

Результат — 0.33, ошибка — 45%.

Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение δ (дельта) по формуле 1.
Так как у выходного нейрона нет исходящих синапсов, то мы будем пользоваться первой формулой (δ output), следственно для скрытых нейронов мы уже будем брать вторую формулу (δ hidden). Тут все достаточно просто: считаем разницу между желаемым и полученным результатом и умножаем на производную функции активации от входного значения данного нейрона. Прежде чем приступить к вычислениям я хочу обратить ваше внимание на производную. Во первых как это уже наверное стало понятно, с МОР нужно использовать только те функции активации, которые могут быть дифференцированы. Во вторых чтобы не делать лишних вычислений, формулу производной можно заменить на более дружелюбную и простую формула вида:

Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.

O1output = 0.33
O1ideal = 1
Error = 0.45

δO1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148

На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для H1:

H1output = 0.61
w5 = 1.5
δO1 = 0.148

δH1 = ( (1 — 0.61) * 0.61 ) * ( 1.5 * 0.148 ) = 0.053

Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так:

Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:

H1output = 0.61
δO1 = 0.148

GRADw5 = 0.61 * 0.148 = 0.09

Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом:

Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.

Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, α (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему Δw5.

E = 0.7
Α = 0.3
w5 = 1.5
GRADw5 = 0.09
Δw5(i-1) = 0

Δw5 = 0.7 * 0.09 + 0 * 0.3 = 0.063
w5 = w5 + Δw5 = 1.563

Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для H2.

GRADw6 = 0.69 * 0.148 = 0.1

Δw6 = 0.7 * 0.1 + 0 * 0.3 = 0.07

И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.

Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.

H2input = 1 * 0.73 + 0 * 0.124 = 0.73
H2output = sigmoid(0.73) = 0.675

Результат — 0.37, ошибка — 39%.

Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала.

Что еще нужно знать о процессе обучения?

Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).

Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.

Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.

Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.

Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.

Вкратце о каждом методе:

Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел Δw, сразу обнови соответствующий вес.

Пакетный метод же работает по другому. Мы суммируем Δw всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.

Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму Δw всех весов в той или иной группе.

Что такое гиперпараметры?

Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:

Что такое сходимость?

Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС.

Что такое переобучение?

Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом.

Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться.

Источник