найти точку максимума функции что значит

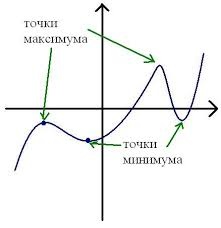
Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.

\(- 9\): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является \(-2\).

Источник

Найдите точку максимума функции

77419.Найдите точку максимума функции у=х 3 –48х+17

Найдём производную заданной функции:

Найдем нули производной:

Определим знаки производной функции подставляя значения из интервалов в полученную производную, и изобразим на рисунке поведение функции:

Получили, что в точке –4 производная меняет свой знак в положительного на отрицательный. Таким образом, точка х=–4 это искомая точка максимума.

77423. Найдите точку максимума функции у=х 3 –3х 2 +2

Найдём производную заданной функции:

Приравняем производную к нулю и решим уравнение:

Определим знаки производной функции и изобразим на рисунке интервалы возрастания и убывания функции подставляя значения из каждого интервала в выражение производной:

В точке х=0 производная меняет знак с положительного на отрицательный, значит это есть точка максимума.

77427. Найдите точку максимума функции у=х 3 +2х 2 +х+3

Найдём производную заданной функции:

При равняем производную к нулю и решим уравнение:

Определим знаки производной функции и изобразим на рисунке интервалы возрастания и убывания функции подставляя значения из каждого интервала в выражение производной:

В точке х=–1 производная меняет знак с положительного на отрицательный, значит это есть искомая точка максимума.

77431. Найдите точку максимума функции у=х 3 –5х 2 +7х–5

Найдём производную функции:

Найдем нули производной:

Решая квадратное уравнение получим:

*Это точки возможного максимума (минимума) функции.

Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:

3∙0 2 – 10∙0 + 7 = 7 > 0

3∙2 2 – 10∙2 + 7 = – 1 2 – 10∙3 + 7 = 4 > 0

В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

77435. Найдите точку максимума функции у=7+12х–х 3

Найдём производную функции:

Найдем нули производной:

Решая квадратное уравнение получим:

*Это точки возможного максимума (минимума) функции.

Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:

12 – 3∙(–3) 2 = –15 2 = 12 > 0

12 – 3∙3 2 = –15

В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

*Для этой же функции точкой минимума является точка х = – 2.

77439. Найдите точку максимума функции у=9х 2 –х 3

Найдём производную функции:

Найдем нули производной:

Решая уравнение получим:

*Это точки возможного максимума (минимума) функции.

Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:

18 (–1) –3 (–1) 2 = –21 2 = 15 > 0

18∙7 –3∙7 2 = –1

В точке х=6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

*Для этой же функции точкой минимума является точка х = 0.

Источник

Как найти точки минимума и максимума функции

Минимум и максимум функции

Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:

Точка минимума, минимум функции

Минимум функции — значение функции в точке минимума \(x_0\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.

Точка максимума, максимум функции

Максимум функции — значение функции в точке максимума \(x_0\)

Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.

Точки максимума и минимума на графике:

Исследование функций на экстремумы

Теорема. Если функция f(x) имеет экстремум в точке \(x=x_0,\) то в ней производная либо равна 0, либо не существует.

Алгоритм нахождения экстремумов с помощью производной:

Найти область определения функции — D(y).

Определить производную — f ‘(x).

Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).

Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).

Вычислить значения функции в точках экстремума.

Примеры задач

Задача 1

Исследовать на экстремумы функцию \(f(x)=x^3-3x^2.\)

Решение задачи по алгоритму:

3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:

5) Найдем значение экстремумов функции.

Задача 2

Задача 3

Докажите, что функция \(f(x)=x^5+2x^3-4\) возрастает на всех числовой прямой.

Источник

Этот раздел содержит задачи ЕГЭ по математике на темы, связанные с исследованием функций и их производных. В частности, речь идёт о поиске максимальных и минимальных значений функций, заданных аналитически, то есть формулой.

Точкой максимума ( минимума ) функции y = f(x) называется значение аргумента x = a такое, что существует окрестность точки a, в которой f(x) ( f(x) > f(a) ) для x ≠ a.

Максимумом ( минимумом ) функции называется её значение в точке экстремума, т.е. величина f(a).

Что касается наибольших и наименьших значений функции на заданном отрезке, то для непрерывной функции они могут достигаться как внутри отрезка, так и на его концах. Графические иллюстрации к этой теме можно посмотреть здесь.
Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка совпадает с точкой соответствующего экстремума. Для ответа на такой вопрос задания следует сравнить значения функции в точках экстремума с её значениями на концах отрезка. (На практике для решения этой задачи не обязательно определять вид экстремума, достаточно вычислить значения функции в критических точках и на концах отрезка и сравнить их между собой.)

В 2022 году это задание имеет номер 11.

Задачи на нахождение точек экстремума функции.

Алгоритм нахождения точек экстремума.

1) Найти область определения функции.
2) Найти её производную f ‘(x).
3) Найти точки, в которых f ‘(x) не существует.
4) Найти точки в которых f ‘(x) = 0.
5) Отметить на числовой прямой область определения функции и все точки, выявленные в п.3 и п.4. Получатся промежутки области определения, на которых производная сохраняет постоянный знак.
6) Определить знак f ‘(x) для каждого промежутка. (Чаще всего это делается подстановкой «удобного» значения x из этого промежутка в полученную в п.2 формулу для производной.)
7) Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере в каждой из критических точек.

Найдите точку максимума функции y = (x + 7)·e 7 − x .

1) Функция представляет собой произведение линейной и показательной функций, которые определены на всей действительной оси.
D(f) = (−∞;∞).

3) Выражение −e 7 − x ·(x + 6) определено во всех точках действительной оси.
Точек, где y’ не существует, нет.

5) Изображаем «бесконечную» числовую ось, совпадающую в нашем случае с областью определения функции. Отмечаем на ней единственную найденную критическую точку x = −6.

6) Определяем знаки производной на получившихся двух участках оси.
При x 7 − x ·(x + 6) = −e 7 + 10 ·(−10 + 6) = −e 17 ·(−4) = 4e 17 ≈ 4·2,7 17 > 0.
При x > −6, например при x = 7, имеем
y’ = −e 7 − x ·(x + 6) = −e 7 − 7 ·(7 + 6) = −e 0 ·13 = −1·13 = −13 0 и знаком «−», где y’ Внимание: Для усиления обучающего эффекта ответы и решения загружаются отдельно для каждой задачи последовательным нажатием кнопок на желтом фоне. (Когда задач много, кнопки могут появиться с задержкой. Если кнопок не видно совсем, проверьте, разрешен ли в вашем браузере JavaScript.)

Найдите точку минимума функции y = 4x − ln(x + 11) + 12.

По определению логарифма x + 11 > 0, следовательно D(f) = (−11;+∞).

В производной x ≠ −11, но это значение не входит в область определения функции, поэтому критической точкой не является.

Следовательно, x = −10,75 точка минимума функции.

По определению арифметического корня 16 − 4x − x 2 ≥ 0. Полностью решать это неравенство пока не будем. Заметим только, что это квадратное неравенство и ветви соответствующей параболы направлены вниз. Можно сделать вывод, что неотрицательные значения квадратный трёхчлен будет иметь на участке между его корнями. D(f) = [x₁ ; x₂].

y’ не существует в точках, где знаменатель дроби равен нулю, т.е.
при 16 − 4x − x 2 = 0. Эти точки мы уже обозначили x₁ и x₂. Они являются краями области определения функции.

Выбираем значения x для проверки знаков производной на получившихся двух участках. Пусть это будут −3 и 0. Убедимся, что не промахнулись мимо области определения функции, т.е. в том, что для этих точек выполняется неравенство для подкоренного выражения. (Если бы мы сразу дорешали неравенство до конца, то этого делать бы не пришлось. Точки выбирались бы по рисунку.)
16 − 4x − x 2 ≥ 0.
16 − 4·(−3) − (−3) 2 = 19 ≥ 0.
16 − 4·0 − 0 2 = 16 ≥ 0.
Определяем знаки производной в этих точках

y’(−3) = − −3 + 2 _____ √19 __ = 1 ___ √19 __ > 0.

y’(0) = − 0 + 2 ____ √16 __ = − 2 _ 4 = −0,5

Следовательно, x = −2 точка максимума функции.

Замечание: Для кого-то может оказаться легче сразу решить квадратное уравнение и рисовать итоговый чертёж явно. Делайте так.
В данном случае x₁ = −2 − 2 √5 _ ≈ −6,5; x₂ = −2 + 2 √5 _ ≈ 2,5.

Найдите точку минимума функции y = (0,5 − x)cosx + sinx, принадлежащую промежутку (0, π/2).

Точек, где y’ не существует, нет.

Замечание: sin0,45 и sin0,55 положительны, т.к. исследуемый интервал соответствует первой четверти тригонометрического круга.

Задачи на нахождение экстремумов функции.

1) Находим точки экстремумов функции и определяем их характер так же, как в задачах выше.
2) Определяем значения функции в точках максимума или минимума в соответствии с вопросом задачи.
3) Если точек максимума (минимума) на области определения функции несколько, то максимумы (минимумы) называются локальными, а самый большой (самый маленький) называется глобальным максимумом (минимумом) или наибольшим (наименьшим) значением функции. Ещё раз читаем вопрос задачи и выбираем нужный.

Первая часть решения полностью совпадает с решением задачи 3.

y’ не существует в точках −5 и 1.

y’(−3) = 1 __ √8 _ > 0; y’(0) = − 2 __ √5 _ √5 − 4x − x 2 __________
y(−2) = √5 − 4·(−2) − (−2) 2 _______________ = √9 _ = 3.
По стрелкам на рисунке видно, что максимум на всей области определения функции единственный, поэтому полученное значение y(−2) = 3 и будет наибольшим значением функции.

Найдите наименьшее значение функции y = log₃(x 2 − 6x + 10) + 2.

По определению логарифма x 2 − 6x + 10 > 0. Дискриминант этого квадратного трёхчлена D = 36 − 40 коэффициент при x 2 равен 1 > 0, следовательно все его значения положительны. Область определения функции D(f) = (−∞;+∞).

Знаменатель этой дроби > 0 (ln3 > 1, т.к. 3 > e ≈ 2,7), поэтому точек, где y’ не существует, нет.

Найденная точка экстремума единственная на области определения функции, разбивает её на два участка, причем при x 3 y’ > 0, значит это точка глобального минимума.

Находим значение функции в этой точке
y(3) = log₃(x 2 − 6x + 10) + 2 = log₃(3 2 − 6·3 + 10) + 2 = log₃1 + 2 = 0 + 2 = 2.
Это наименьшее значение функции на всей области определения.

Задачи на определение наибольшего (наименьшего) значения функции на отрезке.

Непрерывная на отрезке функция достигает своего наименьшего и наибольшего значений либо во внутренних точках промежутка, либо на его концах. Поэтому для решения задач этого раздела достаточно определить значения функции в точках экстремума и сравнить их с её значениями на концах отрезка. Выявлять тип экстремума необязательно.

Находим значения функции в этих точках и на краях отрезка
y(x) = x 3 + 2x 2 + x + 3;
y(−4) = (−4) 3 + 2(−4) 2 − 4 + 3 = −64 + 2·16 − 4 + 3 = −33;
y(−1/3) = (−1/3) 3 + 2(−1/3) 2 − 1/3 + 3 = −1/27 + 2·1/9 −1/3 + 3 = 2 23 __ 27 ;
y(−1) = (−1) 3 + 2·(−1) 2 − 1 + 3 = −1 + 2 − 1 + 3 = 3.

Выбираем самое большое из получившихся значений y. Это y(−1) = 3.

Найдите наибольшее значение функции y = 36tgx − 36x + 9π + 7 на отрезке [−π/4; π/4].

На отрезке [−π/4; π/4] заданная функция определена и непрерывна (см. график tgx).

y’ = 36· _____ 1 cos 2 x − 36 + 0;

y’ не существует при cosx = 0, x_n = _ π 2 ·n, n Є Z. Ни одна из этих точек не входит в промежуток [−π/4; π/4].

y’ = 0 при cos 2 x = 1, cosx = ±1, x_k = πk, k Є Z. Отрезку [−π/4; π/4] принадлежит только точка x₀ = 0.

Определяем значения функции в этой точке и на концах отрезка.
y(x) = 36tgx − 36x + 9π + 7
y(0) = 36tg0 − 36·0 + 9π + 7 = 0 − 0 + 9π + 7 ≈ 9·3,14 + 7 = 35,26
y(−π/4) = 36tg(−π/4) − 36·(−π/4) + 9π + 7 = 36·(−1) + 9π + 9π + 7 = −29 + 18π ≈ −29 + 18·3,14 = 27,52
y(π/4) = 36tg(π/4) − 36·π/4 + 9π + 7 = 36·1 − 9π + 9π + 7 = 43.
Самым большим из этих чисел является число 43.

Функция определена и непрерывна при всех x > 0, в том числе и на отрезке [ 13 __ 14 ; 15 __ 14 ].

y’ не существует при x = 0. Эта точка не входит в заданный промежуток. Не рассматриваем.

y’ = 0 при 4x 2 − 13x + 9 = 0
Решаем это квадратное уравнение через дискриминант, находим корни x₁ = 1, x₂ = 9/4 = 2,25.

x₁ = 1 является серединой заданного отрезка, x₂ = 2,25 не принадлежит отрезку. Значит нужно определить значения функции y(13/14), y(1) и y(15/14) и сравнить их между собой. Однако в данном случае вычисление значений y(13/14) и y(15/14) может оказаться слишком громоздким и с большой вероятностью привести к ошибкам. Проще вернуться к исследованию поведения производной в окрестности найденной точки экстремума.

Определяем его
y(x) = 2x 2 − 13x + 9lnx + 8
y(1) = 2·1 2 − 13·1 + 9·ln1 + 8 = 2 − 13 + 9·0 + 8 = −3.

Найдите наименьшее значение функции y = x 2 + 25 ______ x на отрезке [1;10].

На отрезке [1;10] функция определена и непрерывна (x = 0 не принадлежит отрезку).

y’ не существует при x = 0. Эта точка не входит в заданный промежуток.

x₁ = −5 не принадлежит отрезку [1;10], x₂ = 5 внутренняя точка отрезка.
Находим значения функции

y(1) = 1 2 + 25 ______ 1 = 26;

y(5) = 5 2 + 25 ______ 5 = 10;

y(10) = 10 2 + 25 _______ 10 = 12,5.

Наименьшее значение y(5) = 10.

Вернуться к списку заданий первой части профильного уровня ЕГЭ по математке.

Нашли опечатку или ошибку? Пожалуйста, сообщите о ней.
E-mail: mathematichka@yandex.ru

Внимание, © mathematichka.
Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.

Источник