натуральный логарифм единицы равен чему
Логарифм. Натуральный логарифм.
За основание логарифмов нередко берут цифру е = 2,718281828. Логарифмы по данному основанию именуют натуральным. При проведении вычислений с натуральными логарифмами общепринято оперировать знаком ln, а не log; при этом число 2,718281828, определяющие основание, не указывают.
Само число е определяет предел монотонной ограниченной последовательности
Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!
На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.
График натурального логарифма (функции y = ln x) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:
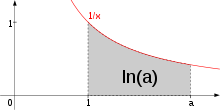
Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a.
Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».
Если анализировать натуральный логарифм, как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:
По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:
Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.
Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x. Он монотонно возрастает на своей области определения.
При x →0 пределом натурального логарифма выступает минус бесконечность ( –∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.
Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
ln 1 равен
Здравствуйте!
Помогите ответить на вопрос чему ln 1 равен. Каким образом можно его найти?
Спасибо!
Рассмотрим два варианта вычисления, чему ln 1 равен.
Первый способ аналитический. Поскольку функция ln является логарифмом с основанием е, то ее можно записать следующим образом:
Также известно, что натуральный логарифм является функцией, обратной к экспоненциальной функции. Отсюда следует, что натуральный логарифм единицы равен показателю степени, в которую нужно возвести экспоненту, чтобы получить число 1. Как известно, число е равно приблизительно 2,71. А степень любого числа, которое вознести в степень, получив при этом единицу, будет равна нулю. Следовательно, натуральный логарифм единицы равна нулю. Запишем это аналитически:




С помощью графика натурального логарифма значение его от единицы можно определить гораздо быстрее. Найдем на графике значение х=1. При этом значении аргумента график самой функции ln будет пересекать ось абсцисс, соответственно значение натурального логарифма будет равно 0.
Зная основные свойства натурального логарифма и экспоненциальной функции нужное значение можно вычислить и с помощью калькулятора.
Также довольно часто для вычисления значений натуральных логарифмов и других функций используют онлайн калькуляторы.
Натуральный логарифм
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Содержание
История
Конвенции об обозначениях
Русская (и советская в целом) система
Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Англо-американская система
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «loge(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log10(x).
В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log2(x)» (хотя часто вместо этого пишется просто lg(x)).
Техника
В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.
В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.
Происхождение термина натуральный логарифм
Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей. [5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60. [6] [7] [8]
loge является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции: [9]
Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление. [10]
Определение
Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская 
Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.
Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что 
Свойства
Производная, ряд Тейлора
Производная натурального логарифма равна
На основании этого можно выполнить разложение 

С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:
Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.
Также заметим, что 

Натуральный логарифм в интегрировании
Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:
Ниже дан пример для g(x) = tan(x):


где C — произвольная константа.
Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
 |  |
 |
при условии, что y = (x−1)/(x+1) и x > 0.
Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
 |  |
 | |
 | |
 |
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула: [12] [13]
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

,» border=»0″ />
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:

Комплексные логарифмы
Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.
Натуральный логарифм — определение, свойства и примеры решений
Из-за своего простого вида производная натурального логарифма нашла широкое применение в высшей математике, физике, экономике. Определяется она площадью, образованной гиперболой, и характеризуется рядом свойств. При этом всё, что относится к обычным логарифмам, справедливо и для неё. Для расчёта выражений такого вида используют правила и алгоритмы, делающие вычисления удобными и простыми.
Понятия и термины
Впервые упоминание о логарифмах встречается в античные времена. Толчком, послужившим для выделения понятия в отдельное выражение, стало открытие свойств степеней. Из-за стремительного развития архитектуры и строительства, астрономических исследований в средневековой Европе, Индии и Китае возник спрос на сложные расчёты. Так, вместо умножения при возведении в степень стали использовать логарифмирование — тождественную операцию.
В формуле log обозначает степенную функцию, n — основание, y — аргумент. Читается такая запись, как икс, равный логарифму игрек по основанию эн. В 1614 году шотландец Непер предложил таблицу логарифмов тригонометрических функций и описал их свойства. Несмотря на неточности в их вычислении, его расчёты вызвали восторг в математическом мире. Через пять лет английский учитель Спайделл внёс свои корректировки в таблицы и фактически предложил сборник натуральных логарифмов.
До начала XX века общепринятого обозначения выражения не существовало. Пока операция, заменяющая собой возведение в степень, не была подробно описана в книге «Введение в анализ бесконечных» Эйлера, который выделил и разделил все известные выражения логарифмов на три вида:
Использование в основании натурального логарифма математической константы e играет важную роль в математическом анализе. Иррациональное число принимается равным 2,71828. Её функция дифференцируется и интегрируется «в саму себя». Поэтому запись, в основании которой стоит такое число, и назвали натуральным.
Таким образом, логарифм, у которого по основанию находится постоянная e, называют также натуральным. Математически это определение записывают в виде выражения: ln c = loge c.
Функция выражения
График натурально-логарифмической функции сходен с обычной, но имеет меньшую крутизну. К основным свойствам функции относят:
Формула ∫ ln p dp = p ln p — p + C является интегралом функции натурального логарифма. Выводится она с помощью метода интегрирования по частям: ∫ i dk = i * k — i dk. В заданном интеграле можно выделить функции i и k и отдельно выполнить их интегрирование. Тогда исходное выражение будет разложено на две части. Первая будет иметь вид: i = ln p, di = dp / p, а вторая — dk = dp, k = p. Соответственно, выполняя подстановку, можно записать следующее равенство: p ln p — ∫ dp = p ln p — p + C.
Иными словами, простая интегральная первообразная функция g (p) = f'(p) / f (x) будет иметь вид: ln |f (p)|. Это также следует из цепного правила и факта: d / dp (ln |p|) = 1/p. Последнее выражение можно переписать как ∫ dx / x = ln |x| + C, где свободный член — произвольная константа. В соответствии: ∫ f'(x) / f (x) dx =ln |f (x)| + C.
Свойства логарифма
Натуральное логарифмическое выражение характеризуется основной формулой сложения и вычитания. Согласно ей, функцию вида ln (x * y) справедливо преобразовать в сумму ln x + ln y. Аналогично, если в основании стоит знак деления, то его можно заменить разностью: ln (x/y) = ln x — ln y. Это свойство логарифма используется довольно часто при преобразованиях сложных уравнений.
Кроме этого, можно выделить следующие основные формулы, использующиеся при решениях заданий различной сложности:
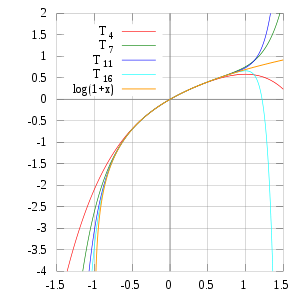
Рассматриваемый логарифм можно разложить в степенной ряд. В нём слагаемыми служат действительная функция p © и её производные, делённые на факториал. Это преобразование называют разложение Маклорена. Для натурального выражения оно будет иметь вид: ln (1+c) = c — c 2 /2 + c 3 /3 — …+ (-1) n+1 * c n / n +…, при условии, что значение икса по модулю меньше единицы.
Примеры типовых заданий
Знание теоретических основ позволяет довольно легко вычислять натуральные выражения практически любой сложности. Самые простые задания даются для закрепления основных формул. Поэтому они обычно состоят из нескольких шагов. Например, нужно вычислить выражение: ln 2 * e 2 + ln 1/ (2* e). Применяя свойство степеней, заданное выражение можно привести к виду: ln (2 * e 2 * 1 / (2 * e). После сокращения числителя и знаменателя на 2 * e, исходное выражение станет равным ln e. Таким образом, ln 2 * e 2 + ln 1/ (2* e) = ln e = 1.
Следовательно, область решений неравенства будет принадлежать p Є (1/ e; e 2 ). Следует обратить внимание, что использование замены для упрощения является одним из ключевых моментов в решении логарифмов.
Использование онлайн-калькулятора
При нахождении логарифмов в реальных условиях довольно часто приходится сталкиваться с громоздкими вычислениями. Такие расчёты требуют внимания и скрупулёзности. Ведь даже небольшая ошибка в итоге может привести к неправильному результату. При этом расчёт часто занимает продолжительное время.
В интернете существует несколько десятков сайтов, предоставляющих услуги по расчёту логарифмов онлайн. Это так называемые онлайн-калькуляторы. Доступ к ним может получить любой заинтересованный пользователь. Для этого ему просто понадобиться интернет и браузер с поддержкой Flesh технологи.
На страницах таких сервисов встроена специальная программа на языке Java. Фактически это аналог ранее популярных отдельных приложений, написанных на двоичном коде в Паскале. От пользователя требуется лишь вести в предложенную форму уравнение и нажать кнопку «Рассчитать». Приложение самостоятельно выберет нужные формулы и по ним рассчитает ответ.
Кроме конечного ответа, онлайн-сервисы предлагают подробный пошаговый расчёт. Это очень полезно для учащихся, которые пробуют разобраться в премудростях вычисления логарифма. А также для них на страницах предоставляется теоретический материал с примерами различной сложности. Примечательно и то, что доступ к сайтам обычно не только бесплатный, но и не требует какой-либо регистрации или указания личных данных.
По мнению пользователей рунета, из нескольких десятков существующих сайтов на русском языке можно выделить пятёрку лидеров:
Эти онлайн-калькуляторы имеют интуитивно понятный интерфейс и всю необходимую теорию для понятия принципа нахождения логарифма. Решив несколько заданий с их помощью, пользователь сможет самостоятельно вычислять любые логарифмические выражения. Таким образом, расчётчики смогут как подтянуть знания, так и проверить полученный ответ. Ведь появление ошибки при использовании программы практически невозможно.