направляющий вектор прямой что такое
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
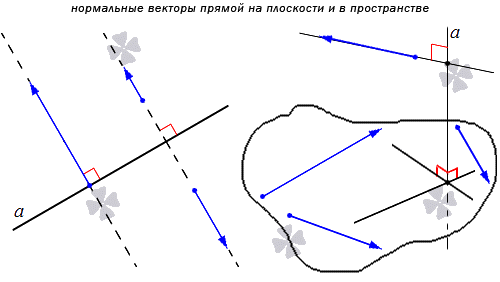
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
Для решения можно выбирать любой удобный способ.
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
Большая Энциклопедия Нефти и Газа
Направляющий вектор прямой определен неоднозначно. Как сказывается эта неоднозначность на определении угла между прямыми. [1]
Направляющим вектором прямой называется всякий вектор s, параллельный этой прямой. [2]
Направляющим вектором прямой называется любой ненулевой вектор, который лежит на этой прямой. [3]
Что называется направляющим вектором прямой в пространстве. [6]
В качестве f возьмем направляющий вектор прямой /, имеющий ( как следует из канонических уравнений прямой /) координаты 1 1 1 в базисе ei, e2, ез. [9]
Отметим, что начальная точка и направляющий вектор прямой образуют на этой прямой ее внутреннюю де-картову систему координат. Значение параметра t, соответствующее какой-либо точке, является координатой этой точки по отношению к внутренней системе координат. [10]
Отметим, что начальная точка и направляющий вектор прямой образуют на этой прямой ее внутреннюю де-картову систему координат. Значение параметра t, соответствующее какой-либо точке, является координатой этой точки по отношению к внутренней системе координат. [11]
Вектор с компонентами ( 22) есть направляющий вектор прямой ( 20), какова бы ни была декартова система координат. [12]
Вектор с компонентами ( 19) будет направляющим вектором прямой ( 17), какова бы ни была декартова система координат. [13]
В частности, прямая параллельна плоскости, если направляющие векторы прямой и плоскости взаимно перпендикулярны, и, наоборот, прямая перпендикулярна плоскости, если она параллельна направляющему вектору плоскости. [15]
2.2.3. Как найти направляющий вектор
по общему уравнению прямой?
Если прямая задана общим уравнением 
, то вектор 
является направляющим вектором данной прямой.
Примеры нахождения направляющих векторов прямых: 
Утверждение позволяет найти лишь один направляющий вектор из бесчисленного множества, но нам больше и не нужно. Хотя в ряде случаев координаты направляющих векторов целесообразно сократить: так, уравнение 
задаёт прямую, которая параллельна оси 
и координаты полученного направляющего вектора 
удобно разделить на –2, получая в точности базисный вектор 
в качестве направляющего вектора. Аналогично, уравнение 
задаёт прямую, параллельную оси 
, и, разделив координаты вектора 
на 5, получаем направляющий вектор 
.
Читателям с низким уровнем подготовки рекомендую постоянно выполнять чертежи, чтобы лучше понимать мои объяснения!
Теперь выполним проверку Задачи 61. Решение уехало вверх, поэтому напоминаю, что в ней мы составили уравнение прямой 
по точке 
и направляющему вектору 
. Проверка состоит в двух действиях:
Во-первых, по уравнению прямой 
восстанавливаем её направляющий вектор: 
– всё нормально, получили исходный вектор (в ряде случаев может получиться коллинеарный исходному вектор, и это несложно заметить по пропорциональности соответствующих координат).
Во-вторых, координаты точки 
должны удовлетворять уравнению 
. Подставляем их в уравнение: 
– получено верное равенство, чему мы очень рады.
Вывод: задание выполнено правильно.
Задача 62
Составить уравнение прямой по точке 
и направляющему вектору 
Это задача для самостоятельного решения. И проверка, проверка, проверка!
Старайтесь всегда (если это возможно) выполнять проверку на черновике.
Глупо допускать ошибки там, где их 100%-но можно избежать!
В том случае, если одна из координат направляющего вектора равна нулю, поступают очень просто:
Задача 63
Составить уравнение прямой по точке 
и направляющему вектору 
.
Решение: формула 
не годится, так как знаменатель правой части равен нулю. Но выход прост! Используя свойства пропорции, перепишем уравнение в виде 
, и дальнейшее покатилось по глубокой колее: 
переставим части местами: 
Ответ: 
Проверка:
1) Восстановим направляющий вектор найденной прямой 
:
– полученный вектор коллинеарен исходному направляющему вектору 
.
2) Подставим координаты точки 
в уравнение 
: 
– получено верное равенство, значит, точка 
удовлетворяет уравнению.
Вывод: задание выполнено правильно
Возникает вопрос: зачем маяться с формулой 
, если существует универсальная версия 
, которая сработает в любом случае?
Причин две. Во-первых, формула в виде дроби 
гораздо лучше запоминается. А во-вторых, недостаток универсальной формулы 
состоит в том, что здесь повышается риск запутаться при подстановке координат.
Задача 64
Составить уравнение прямой по точке 
и направляющему вектору 
, выполнить проверку.
Это задача для самостоятельного решения. Кстати, проверку можно выполнять и графически – решили задачу и изобразили всё на чертеже. Правда, такой способ бывает неудобен или трудновыполнИм, и поэтому всё-таки «рулит» аналитика.
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением 
в декартовой системе координат, то вектор 
является вектором нормали данной прямой.
Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения: 
И тут всё ещё проще: если координаты направляющего вектора 
приходилось аккуратно «вытаскивать» из уравнения, то координаты вектора нормали 
достаточно просто «снять».
Приведу примеры с теми же уравнениями, что и для направляющего вектора: 
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».