Что такое зона френеля

Зоны Френеля

Полезное

Смотреть что такое «Зоны Френеля» в других словарях:

ЗОНЫ ФРЕНЕЛЯ — участки, на к рые разбивают поверхность фронта световой волны для упрощения вычислений при определении амплитуды волны в заданной точке пр ва. Метод З. Ф. используется при рассмотрении задач о дифракции волн в соответствии с Гюйгенса Френеля… … Физическая энциклопедия

ФРЕНЕЛЯ — (1) дифракция (см.) сферической световой волны, при рассмотрении которой нельзя пренебречь кривизной поверхности падающей и дифрагировавшей (либо только дифрагировавшей) волн. В центре дифракционной картины от круглого непрозрачного диска всегда… … Большая политехническая энциклопедия

ФРЕНЕЛЯ ЗОНЫ — участки, на которые разбивается волновая поверхность при рассмотрении дифракционных волн (Гюйгенса Френеля принцип). Зоны Френеля выбираются так, чтобы удаление каждой следующей зоны от точки наблюдения было на половину длины волны больше, чем… … Большой Энциклопедический словарь

Френеля зоны — участки, на которые разбивают волновую поверхность при рассмотрении дифракции волн (Гюйгенса Френеля принцип). Зоны Френеля выбираются так, чтобы удаление каждой следующей зоны от точки наблюдения было на половину длины волны больше, чем удаление … Энциклопедический словарь

Френеля дифракция — дифракция сферической световой волны на неоднородности (например, отверстии), размер которой сравним с диаметром одной из зон Френеля (См. Зоны Френеля). Название дано в честь изучившего этот вид дифракции О. Ж. Френеля (См. Френель).… … Большая советская энциклопедия

ФРЕНЕЛЯ ЗОНЫ — участки, на к рые разбивают поверхность фронта световой волны для упрощения вычислений при определении амплитуды волны в заданной точке про странства. Метод Ф. з. используется при рассмотрении задач о дифракции волн в соответствии с Гюйгенса… … Физическая энциклопедия

ФРЕНЕЛЯ ЗОНЫ — участки, на к рые разбивают волновую поверхность при рассмотрении дифракции волн (Гюйгенса Френеля принцип). Ф. з. выбираются так, чтобы удаление каждой след. зоны от точки наблюдения было на половину длины волны больше, чем удаление предыдущей… … Естествознание. Энциклопедический словарь

Источник

Зоны Френеля

Другими словами, радиоволна в процессе распространения движется не только по прямой траектории и не в виде «луча» (хотя лучевые модели распространения радиоволн и применяются в расчете различных задач технической электродинамики). Когда волна перемещается на значительные расстояния, измеряемые сотнями длин волн, она, в результате распространения, занимает некий объем в форме эллипса:

Понятно, что при отсутствии прямой видимости качественная связь на больших расстояниях затруднительна. Но с требованиями к отсутствию препятствий в зоне Френеля все не так однозначно. Наличие препятствий внутри эллипсоида распространения радиоволн может приводить к наводкам, помехам или просто вносить дополнительное затухание (как, например, в случае с лесным массивом).

Если устанавливать радиомост только из условия наличия прямой видимости, то, вероятнее всего, на детекторе качества сигнала вы увидите значение 95-98%. Но при этом скорость передачи данных может оказаться минимальной (из-за потерь и повтора пакетов) по причине наличия препятствий внутри зоны Френеля.

Для расчета радиуса зоны Френеля можно воспользоваться упрощенной, но подтвержденной на практике формулой:

где R – радиус зоны Френеля (м);
S,D – расстояние от антенн до самой высокой точки предполагаемого препятствия (км);
f – частота (ГГц).

Когда радиус зоны Френеля над предполагаемым препятствием рассчитан, нужно понять не занимает ли препятствие больше 40% рассчитанного радиуса:

Что же делать в том случае, если препятствие закрывает большую часть радиуса этого эллипса и свободным от препятствий остается менее 60% зоны Френеля? В этом случае задача организации стабильного радиосигнала решается только путем поднятия антенн на соответствующую высоту, чтобы в месте наличия препятствия зона Френеля была достаточно свободна. После подъема антенн на необходимую высоту на обеих сторонах, линк будет работать на максимальной скорости и с максимальной для данного расстояния отдачей.

Еще следует отметить, что мы живем в трехмерном пространстве (amazing!). Поэтому следует учитывать и препятствия, которые находятся сбоку. Например, в случае построения линка, луч которого проходит между двух зданий, должно соблюдаться то же самое условие:

Таким образом, зона Френеля и, как следствие, размер эллипса определяется частотой работы и расстоянием между двумя конечными точками радиомоста (передатчиком и приемником). При этом отметим, что зона Френеля состоит из нескольких зон, причем зона 1 имеет самый сильный сигнал, а следующие зоны (зона 2 и зона 3) имеют более слабые сигналы:

Исходя из рисунка выше, зона Френеля рассчитывается с использованием следующего уравнения:

Вот еще упрощенная формула для определения радиуса самой широкой точки зоны Френеля (в метрах):

При расчета высоты установки антенн рекомендуем пользоваться следующим онлайн-расчетчиком: Ubiquiti Outdoor Wireless Link Calculator.

Источник

Что такое зона Френеля и CCQ (Client Connection Quality) или фундаментальные факторы качественного беспроводного моста

Содержание

В данной статье хочу поговорить о фундаментальных факторах построения качественного беспроводного моста, так как многие «сете-строители» считают, что вполне достаточно будет купить качественное сетевое оборудование, установить и получить 100% отдачу от них — что в итоге не у всех получается.

CCQ — что это?

CCQ (Client Connection Quality) с английского переводиться как «качество клиентского соединения» — что в принципе показывает процентное соотношение теоретически возможной к реально текущей пропускной способности канала, иными словами процент достигнутой пропускной способности с максимально возможной на конкретном оборудовании.

К примеру, вы используете оборудование с максимально возможно пропускной способностью в 200 мбит/с, а по факту на текущем канале 100 мбит/с — в таком случае CCQ равен 50%

В сетевом оборудовании Mikrotik и Ubiquiti присутствуют два отдельных индикатора
Tx. CCQ (Transmit CCQ) — скорость передачи данных.
Rx. CCQ (Receive CCQ) — скорость приема данных.

Три основных фактора влияющие на качество CCQ

1. Юстировка двух антенн. Если говорить о беспроводном мосте «точка-точка» то понятно что антенны должны смотреть друг на друга максимально точно, «глаза в глаза».

Если нужен wi-fi мост «точка-многоточка» — то изначально нужно продумать всю архитектуру от секторной антенны провайдера до клиентских, так что бы они пересекались максимально точно.

2. Наличие шума в канале. Перед тем как определиться с частотой wi-fi моста, обязательно проверить каждую частоту на наличие шума, исходя из данной проверки остановиться на менее загруженной частоте.

3. Зона Френеля.

Зона Френеля — что это?

Зона Френеля это объем радио-волнового канала между двумя антеннами.

Максимальный объем канала находиться в центральной точке между двумя антеннами.

Для максимально качественного сигнала нужно подобрать наиболее чистую зону, как от физических препятствий, так и от радио-волновых (о чем говорили во втором пункте).

Как рассчитать зону Френеля?

Формула расчета зоны Френеля в центральной ее точке:

D — расстояние (km)
f — частота (GHz)

Формула расчета зоны Френеля в любой ее точке, например в месте препятствия:

f — частота (GHz)
D1 — расстояние до нужной вам точки расчета, от первой антенны (km)
D2 — расстояние до нужной вам точки расчета, от второй антенны (km)

Хорошенько проработав данные три фактора, вы в итоге получите стабильный беспроводной мост, с максимально возможной скоростью передачи данных.

Источник

Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля

Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.

Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.

Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.

Принцип Гюйгенса-Френеля

Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.

Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.

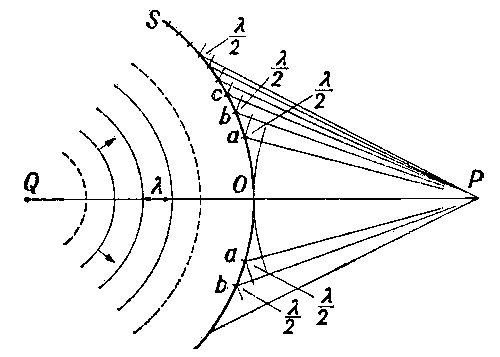
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.

Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.

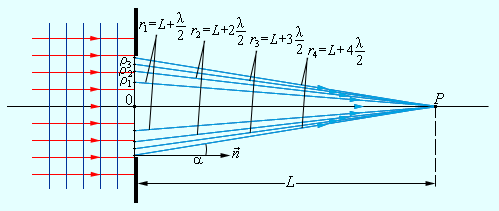
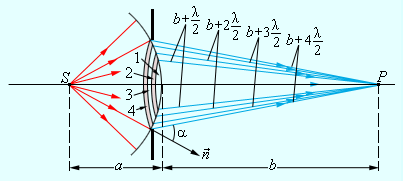
Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.

Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.

Зоны Френеля. Интерференционный максимум

Отличие от двух соседних точек расстоянием λ 2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:

Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.

Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.

Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:

Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.

Получим формулы вида:

Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:

Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.

Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.

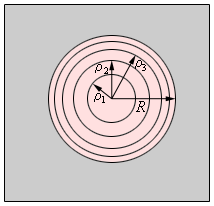
При расчете видно, что радиусы ρ m зон Френеля на волне сферического фронта запишется, как

Выводы по теории Френеля справедливы.

Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.

Источник

Зоны Френеля. Просто о сложном.

Научиться настройке MikroTik можно на онлайн курсе по оборудованию этого производителя. Автор курса является сертифицированным тренером MikroTik. Подробней Вы можете прочитать в конце статьи.

Зоны Френеля используются теорией распространения для расчета отражений и дифракционных потерь между передатчиком и приемником. Зоны Френеля нумеруются и называются «F1», «F2», «F3» и т. д.

Существует бесконечное количество зон Френеля, однако только первые 3 имеют реальное влияние на распространение радиоволн.

Что такое зона Френеля и почему это важно?

Зона Френеля — это цилиндрический эллипс, проведенный между передатчиком и приемником. Размер эллипса определяется частотой работы и расстоянием между двумя участками.

Определяем размер зоны

Когда радиосигнал проходит между передатчиком и приемником, он может распространяться несколькими путями. Он может идти напрямую между передатчиком и приемником (основной сигнал). Сигнал может отражаться от земли и затем переноситься на удаленный приемник (отраженный сигнал). Он может идти влево или вправо и отражаться от «холма» (еще один отраженный сигнал).

Радиус зоны Френеля описывает это отражение относительно общей длины радиотрассы. Рисунок выше показывает основные и отраженные сигналы и F1 (первая зона Френеля) и F2 (вторая зона Френеля). Отражение может происходить в любом месте между передатчиком и приемником. На рисунке показано отражение, происходящее в случайном месте, а не в центре пути.

Когда сигнал отражается, происходят две вещи:

ВАЖНО! На длинном пути сдвиг может составить 180º или больше.

Почему это важно? Приемная антенна не может различить основной и отраженный сигналы. Они оба на одной частоте. Он принимает как основной, так и отраженный сигналы. Он также получает любые другие сигналы в пределах своего заданного диапазона частот.

Когда антенна получает основной сигнал и отраженный сигнал, эти два сигнала будут объединяться и суммироваться на антенне. Если они сдвинуты на 360º (по фазе), это не проблема. Однако, если сигналы разнесены на 180º (противоположная фаза), они будут взаимно поглощаться, и приемник ничего не получит.

Метод зон Френеля

Для нахождения результата интерференции вторичных волн Френель предложил метод разбиения волнового фронта на зоны, называемые зонами Френеля.

Зона Френеля 1 (F1)

Радиус первой зоны Френеля рассчитывается так, чтобы разница в длине пути между основным сигналом и отраженным сигналом от расстояния радиуса F1 составляла 180º. Отраженный сигнал, смещенный на 180º расстояния пути плюс 180º от фактической точки отражения, составляет 360º фазового сдвига. Два сигнала, основной и отраженный, поступают на антенну на 360º друг от друга или в фазе. Они будут складываться и не влияют на производительность приемника.

Этот сдвиг фазы отражения может происходить в любом месте от вычисленной «трубки» зоны Френеля, известной как эллипс.

Зона Френеля 2 (F2)

Радиус второй зоны Френеля рассчитывается так, чтобы разница в длине пути между основным и отраженным сигналами от второй трубки зоны Френеля составляла 360º.

Это очень важно, так как отраженный сигнал имеет автоматический фазовый сдвиг на 180º плюс разница в длине пути 360º равна сдвигу фазы 540º. 540º и 180º имеют одинаковый фазовый сдвиг в математической модели, и два сигнала будут отменены, не оставляя сигнала на приемнике.

Вторая зона Френеля, F2, является зоной отражения, которая не учитывается при проектировании радиотрассы.

Зона Френеля 3 (F3)

Третья зона Френеля имеет разницу в длине пути 540º. Добавьте это к сдвигу отражения 180º; общее количество составляет 720º, и 2 сигнала находятся в фазе.

Эффект зоны Френеля

Конечным результатом является то, что четные зоны Френеля отражают сигнал 180 градусов. Это вредно для распространения по радио. Зоны Френеля с нечетным номером имеют фазовый сдвиг на 360º и не имеют никакого эффекта. Нечетные зоны Френеля — это «хорошие парни».

Эффект этих отражений в мобильной работе может ощущаться, например, вблизи крайнего конца ретранслятора.

В приемнике слышно быстрое увеличение / уменьшение сигнала, которое часто называют «пикетным ограждением».Быстрое увеличение и уменьшение сигнала от движущегося радио или транспортного средства называется замиранием Рэлея. Это является прямым результатом появления и исчезновения отражений в зоне Френеля, когда транспортное средство движется по шоссе.

Радиотерминалы «точка-точка»

Радиосвязи точка-точка обсуждаются далее в этой статье, однако стоит отметить одну хитрость при проектировании линий связи точка-точка.

Поскольку зона F2 вредна для уровня принимаемого сигнала, высоту антенны часто выбирают таким образом, чтобы F1 была беспрепятственной траекторией, а F2 препятствовала возвышению или утолщению земли вдоль трассы.

Любые 180º отраженные сигналы вдоль зоны F2 ослабляются холмом или землей и не достигают приемной антенны, чтобы создавать помехи и подавлять основной приемный сигнал.

Радиус зоны Френеля и расстояние до Земли

Диаметр зоны Френеля (половина диаметра — это радиус) эллиптического цилиндра можно рассчитать. Важным компонентом радиуса зоны Френеля является зазор между цилиндром зоны Френеля и поверхностью земли. Как показано на рисунке 2, показаны радиус зоны Френеля и расстояние от нижней части зоны Френеля до Земли.

При превышении 60% радиоканал считается «чистым, прямой видимости» и не несет дифракционных потерь.

Это понимание зон Френеля и их влияния помогает понять, как и почему радиопокрытие может быть предсказано с использованием математики, а теперь и компьютеров.

Дифракция Френеля на круглом отверстии

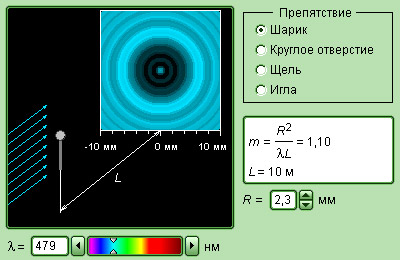
Предположим, что монохроматический луч света падает на экран с круглым отверстием в нем. На определенном расстоянии от отверстия на втором экране можно наблюдать дифракционную картину. Структура рисунка зависит от длины волны, и распределение фаз входящего волнового фронта, а также по диаметру, отверстия и расстояния, от дыры до экрана.

В этом так называемом дифракционном режиме ближнего поля или Френеля монохроматическая плоская или сферическая волна, которая освещает отверстие, будет создавать дифракционную картину в виде набора концентрических колец. Излучение на оптической оси будет минимальным или максимальным, когда при постоянной длине волны и диаметре отверстия расстояние от отверстия до экрана наблюдения уменьшается от бесконечности до нуля.

Кольца появляются после прохождения критического расстояния (также называемого длиной Рэлея):

\( z_p = A \lambda Z_p = A \lambda \)

Если ​ \( r > 3pZ>Z_p \) ​ z > z R «>— колец нет, но наблюдается плавное распределение освещенности в виде квадрата функции Бесселя, форма которого (но не диаметр пучка) остается постоянной при увеличении z. Это дальнее поле также называется дифракцией Фраунгофера.

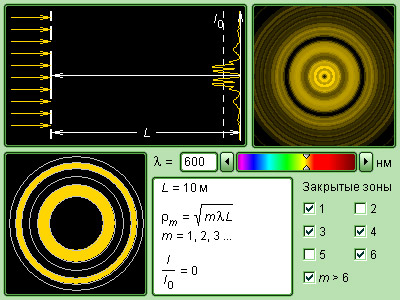
То, появляется ли максимум или минимум на оптической оси, можно понять с помощью теории зон Френеля. Если число полу-лямбда-зон, «видимых» наблюдателем, нечетно, наблюдается максимум, четное количество зон создает минимальное излучение. Количество зон Френеля указывается номером Френеля:

В этих экспериментах измеряются расстояния, на которых появляются максимальная или минимальная интенсивность на оптической оси. Из этих измерений можно определить длину волны света, если известен диаметр отверстия.

В этом упражнении рассматриваются два входящих волновых фронта: плоская волна и сферическая волна.

Дифракция Френеля на маленьком круглом экране

Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути экран с круглым отверстием

Каковы условия для дифракции Френеля?

Дифракция Френеля возникает, когда либо расстояние от источника до препятствия, либо расстояние от препятствия до экрана сравнимо с размером препятствия. Эти сопоставимые расстояния и размеры приводят к уникальному дифракционному поведению.

Почему дифракция Френеля отличается от других видов дифракции?

Как дифракция Френеля решается математически?

Принцип Гюйгенса — Френеля

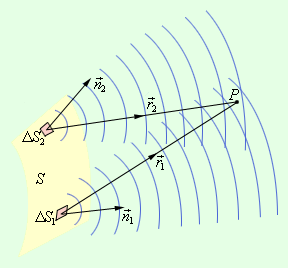
Принцип Гюйгенса-Френеля гласит, что каждая точка на волновом фронте является источником вейвлетов. Эти вейвлеты распространяются в прямом направлении с той же скоростью, что и исходная волна. Новый волновой фронт — это линия, касающаяся всех вейвлетов.

Рис 3. Форма волны

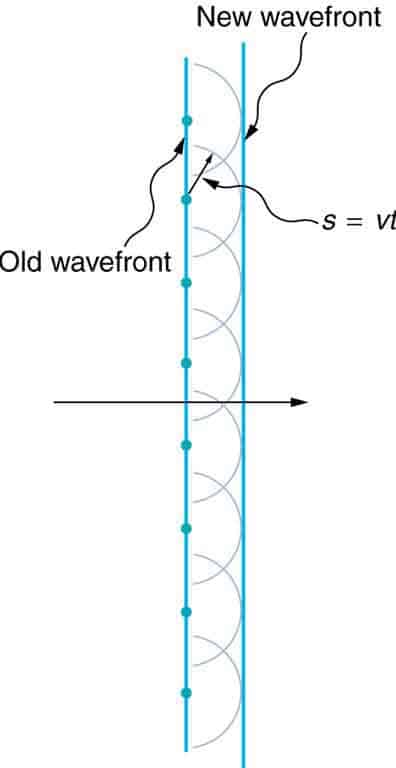
Кристиан Гюйгенс был голландским ученым, который разработал полезную технику для определения того, как и где распространяются волны. В 1678 году он предположил, что каждая точка, к которой относится световое возмущение, сама становится источником сферической волны. Сумма вторичных волн (волн, являющихся результатом возмущения) определяет форму новой волны, показывает вторичные волны, идущие вперед от их источника. Он смог придумать объяснение линейного и сферического распространения волн и вывести законы отражения и преломления (описанные в предыдущих атомах), используя этот принцип. Однако он не мог объяснить то, что обычно называют дифракционными эффектами. Эффекты дифракции — это отклонения от прямолинейного распространения, которое возникает, когда свет сталкивается с краями, экранами и отверстиями.

Прямой волновой фронт: принцип Гюйгенса, применяемый к прямому волновому фронту. Каждая точка на фронте волны излучает полукруглый вейвлет, который перемещается на расстояние:

Новый волновой фронт представляет собой линию, касательную к вейвлетам.

Принцип Гюйгенса

На рисунке показан простой пример дифракционного принципа Гюйгенса. Принцип может быть показан с помощью уравнения ниже:

где s — расстояние, V — скорость распространения, а t — время.

Каждая точка на волновом фронте испускает волну со скоростью V. Испускаемые волны полукруглые и появляются в момент времени t. Новый волновой фронт касается вейвлетов. Этот принцип работает для всех типов волн, а не только для световых волн. Принцип полезен при описании отражения, преломления и интерференции. наглядно показывает, как принцип Гюйгенса может быть использован для объяснения отражения, и показывает, как его можно применять к преломлению.

Рефракция Гюйгенса: принцип Гюйгенса применяется к прямому волновому фронту, перемещающемуся из одной среды в другую, где его скорость меньше. Луч изгибается в направлении перпендикуляра, поскольку вейвлеты имеют меньшую скорость во второй среде.

Отражение : принцип Гюйгенса применяется к прямому волновому фронту, ударяющемуся о зеркало. Показанные вейвлеты испускались, когда каждая точка на фронте волны ударялась о зеркало. Касательная к этим вейвлетам показывает, что новый волновой фронт был отражен под углом, равным углу падения. Направление распространения перпендикулярно фронту волны, как показано стрелками, направленными вниз.

Пятно Пуассона

Пятно Пуассона является доказательством того, что даже если вы правы, вы можете быть не правы. Узнайте, почему эта концепция физики привела к тому, что имя Симеона Пуассона прожило в позоре почти 200 лет.

В начале восемнадцатого столетия Французская академия решила провести товарищеский конкурс. Члены Академии, как и ученые всего мира, заметили, что когда свет перемещался из одной среды в другую, он изгибался. Стекло, вода, гель, все, что позволяет свету проходить через него, даст ему проход, только если он изменит свой ход. Люди могли измерить изгиб света, но были озадачены тем, что заставило это произойти. Французская академия пыталась решить эту проблему, противопоставляя умы разных ученых.

Помните Августина Френеля? Он был инженером и изучал эффекты света. Работая оттуда, он придумал новую идею; свет излучался волнами, перпендикулярными направлению, в котором он проходил. Его идея вызвала волнение, особенно у пуассоновских пэров. Они полагали, что свет путешествовал как ряд частиц, все из которых имели сложные взаимодействия друг с другом. Пуассон, Френель и другие ученые собрались вместе и провели волнующую серию дискуссий о природе света и наблюдаемых эффектах его путешествия через различные среды.

К концу дебатов Пуассон выдвинул аргумент, который, казалось, сжег теорию Френеля до основания и «засолил землю под ней». Если кого-то забрасывают предметами, его лучший шанс избежать травмы — спрятаться за более крупным предметом (по крайней мере, пока ракеты, ищущие тепло, не разрушат его для всех). Спрячьтесь за скалой, и поток гальки отскочит от скалы и пролетит мимо, не задев вас. Если, с другой стороны, человек по пояс в воде и хочет спрятаться от волны, он не будет в безопасности, приседая за скалой. Волны огибают твердые предметы.

Пуассон рассуждал, что если свет действительно был волной, то когда свет включался на совершенно сферическом объекте, световые волны могли бы огибать этот объект. Идеальная симметрия сферы означала, что все световые волны встретятся в точном центре тени позади нее, ведь там люди смогут увидеть яркое пятно света.

Это было нелепо. После выступления, как все закончили смеяться, успешные французские ученые пошли развлечься или выпить что-нибудь в близлежащем заведении. По крайней мере, один человек не присоединился к ним. Доминик Араго, один из судей, понял, что Пуассон описал идеальный эксперимент. Он нашел круглый предмет, он нашел свет, и довольно скоро он нашел это пятно. Что явилось подтверждением словам Пуассона.

Ничего не оставалось, кроме как вручить приз Френелю. Пуассон выдвинул следствие света как волны, которая была настолько нелепой, настолько маловероятной, что это не могло быть объяснено ничем другим. Френель был достаточно умен, чтобы выдвинуть теорию. Пуассон был достаточно умен, чтобы доказать, что Френель прав, и доказать, что он не прав. Несмотря на то, что Доминик Араго действительно прошел тест, крошечная точка света в центре тени сферического объекта всегда называлась Пятном Пуассона. В физике нет вечного движения, но есть постоянные насмешки.

MikroTik: куда нажать, чтобы заработало?
При всех своих достоинствах, есть у продукции компании MikroTik один минус – много разобщенной и далеко не всегда достоверной информации о ее настройке. Рекомендуем проверенный источник на русском языке, где все собрано, логично и структурировано – видеокурс «Настройка оборудования MikroTik». В курс входит 162 видеоурока, 45 лабораторных работ, вопросы для самопроверки и конспект. Все материалы остаются у вас бессрочно. Начало курса можно посмотреть бесплатно, оставив заявку на странице курса. Автор курса является сертифицированным тренером MikroTik.

Источник