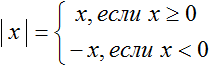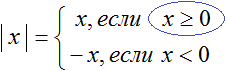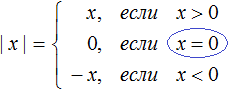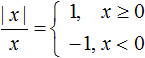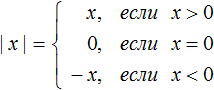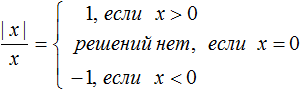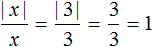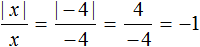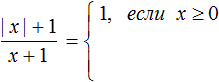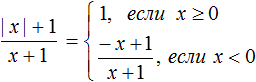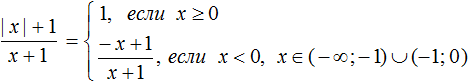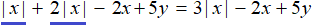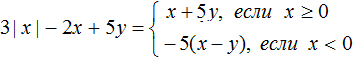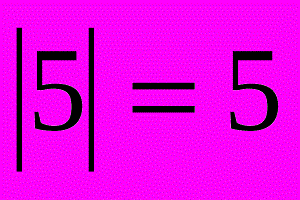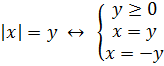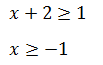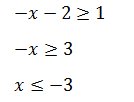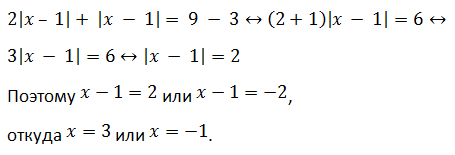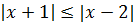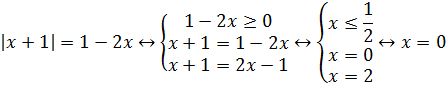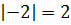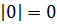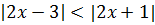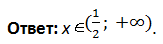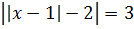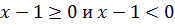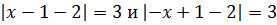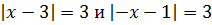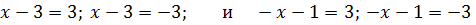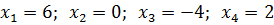Что такое знаки модуля

Обобщённое понятие модуля числа

В данном уроке мы рассмотрим понятие модуля числа более подробно.

Что такое модуль?

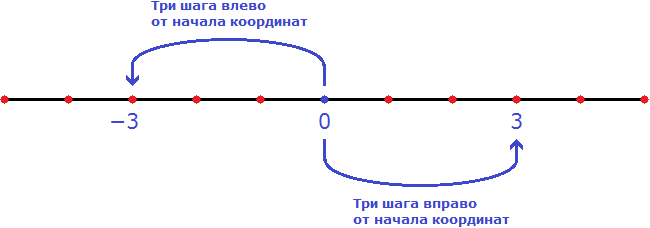
Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3

Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:

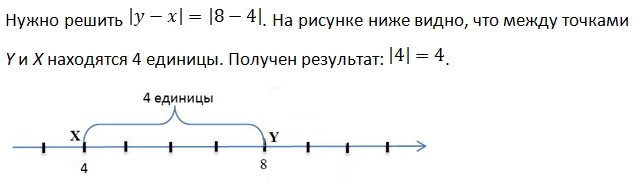
Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:

Где x₁ и x₂ — числа на координатной прямой.

Например, отметим на координатной прямой числа 2 и 5.

Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:

Видим, что расстояние от числа 2 до числа 5 равно трём шагам:

Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3

То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:

Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:

Это равенство можно прочитать так: Расстояние от x₁ до x₂ равно расстоянию от x₂ до x₁.

Раскрытие модуля

Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.

Правило раскрытия модуля выглядит так:

В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.

Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x

Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5

В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0

Поэтому используем первую формулу. А именно | x | = x. Получаем | 5 | = 5.

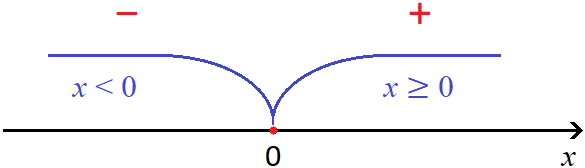
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:

А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:

Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,

Корень из числа 4 равен 2. Тогда модуль примет вид

x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x |√4 − 6| = |2 − 6| = |−4| = −(−4) = 4

На практике обычно рассуждают так:

«Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля».

Примеры:

|2| = 2 — модуль раскрылся со знаком плюс, поскольку 2 ≥ 0

Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:

В данном случае выполняется условие x=0, ведь 0 = 0

Пример 5. Раскрыть модуль в выражении |x|+ 3

Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.

Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:

Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 |x| + 3 = 3 − x = 3 − (−6) = 9

Пример 6. Раскрыть модуль в выражении x +|x + 3|

Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11

Найдём значение выражения x +|x + 3| при x=−3.

Пример 3. Раскрыть модуль в выражении

Как и прежде используем правило раскрытия модуля:

В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0

Перепишем решение так:

Пример 4. Раскрыть модуль в выражении

Но надо учитывать, что при x = − 1 знаменатель выражения 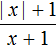обращается в ноль. Поэтому второе условие x следует дополнить записью о том, какие значения может принимать x

Преобразование выражений с модулями

Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.

Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.

Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.

Решение

Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:

В итоге имеем следующее решение:

Пример 2. Раскрыть модуль в выражении: −|x|

Решение

Источник

Модуль числа

Модуль числа и уравнения с модулем — тема особенная, прямо-таки заколдованная 🙂 Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем. И эту картину мы наблюдаем на протяжении многих лет.

Поэтому осваивайте тему «Уравнения и неравенства с модулем» по нашим статьям и на наших занятиях! Вы сумеете обойти множество конкурентов на ЕГЭ, олимпиадах и вступительных экзаменах.

Модуль числа называют ещё абсолютной величиной этого числа. Попросту говоря, при взятии модуля нужно отбросить от числа его знак. В записи положительного числа и так нет. никакого знака, поэтому модуль положительного числа равен ему самому. Например, Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному
(без знака!). Например,

Обратите внимание: модуль числа всегда неотрицателен:

От большинства известных из школы определений оно отличается лишь одним: в нём есть выбор. Есть условие. И в зависимости от этого условия мы раскрываем модуль либо так, либо иначе.

Так же, как в информатике — в разветвляющихся алгоритмах с применением условных операторов. Как, вообще-то, и в жизни: сдал ЕГЭ на минимальный балл — можешь подавать документы в ВУЗ. Не сдал на минимальный балл — можешь идти в армию 🙂

Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению. Например,

В некоторых случаях модуль раскрывается однозначно. Например, так как выражение под знаком модуля неотрицательно при любых x и y. Или: так так как выражение под модулем неположительно при любых z.

Геометрическая интерпретация модуля

Нарисуем числовую прямую. Модуль числа — это расстояние от нуля до данного числа. Например, То есть расстояние от точки −5 до нуля равно 5.
Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем.

Рассмотрим простейшее уравнение . Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения есть два решения: x = 3 и x = −3.

Вообще, если имеются два числа a и b, то равно расстоянию между ними на числовой прямой.
(В связи с этим нередко встречается обозначение длины отрезка AB, то есть расстояния от точки A до точки B.)

Ясно, что (расстояние от точки a до точки b равно расстоянию от точки b до точки a).

Решим уравнение . Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля.

Перейдём к неравенствам. Решим неравенство .

Эту запись можно прочитать так: «расстояние от точки x до точки −7 меньше четырёх». Отмечаем на числовой прямой точки, удовлетворяющие этому условию.

Другой пример. Решим неравенство |10 − x| ≥ 7.

Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
Ответ:

График функции

Этот график надо знать обязательно. Для имеем y = x. Для имеем y = −x. В результате получаем:
С помощью этого графика также можно решать уравнения и неравенства.

Корень из квадрата

Нередко в задачах ЕГЭ требуется вычислить , где – некоторое число или выражение. Не забывайте, что

Действительно, по определению арифметического квадратного корня — это такое неотрицательное число, квадрат которого равен . Оно равно при и при , т. е. как раз .

Примеры заданий ЕГЭ

1. Найдите значение выражения при .
Заметим, что при . Следовательно, значение нашего выражения равно: .

2. Найдите значение выражения при .

В следующей статье мы рассмотрим более сложные уравнения и неравенства с модулем.

Источник

Что такое модуль действительного числа

В данной публикации мы рассмотрим определение, геометрическую интерпретацию, график функции и примеры модуля положительного/отрицательного числа и нуля.

Определение модуля числа

Модуль действительного числа (иногда называется абсолютной величиной) – это величина, равная ему же, если число положительное или равная противоположному, если оно отрицательное.

Модуль числа a обозначается вертикальными черточками с обеих сторон от него – |a|.

Противоположное число отличается от исходного знаком. Например, для числа 5 противоположным является -5. При этом ноль является противоположным самому себе, т.е.

Геометрическая интерпретация модуля

Модуль числа a – это расстояние от начала координат (O) до точки A на координатной оси, которая соответствует числу a, т.е.

График функции с модулем

График четной функции y = |х| выглядит следующим образом:

Чему равняются следующие модули |3|, |-7|, |12,4| и |-0,87|.

Решение:
Согласно приведенному выше определению:

Источник

Модуль числа знак, свойства, действия, как найти, примеры графиков

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

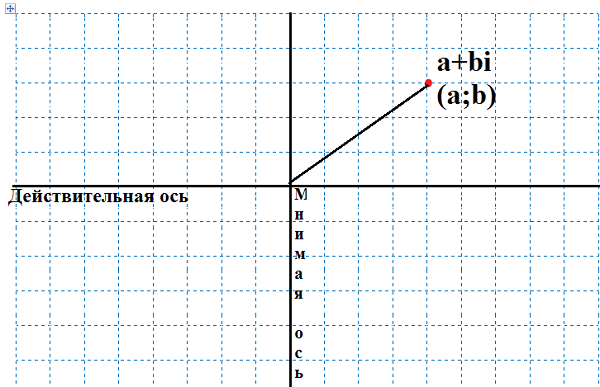
Модуль комплексного числа

Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.

Разделим интервал на 2 части:

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Ответ: x = 0.

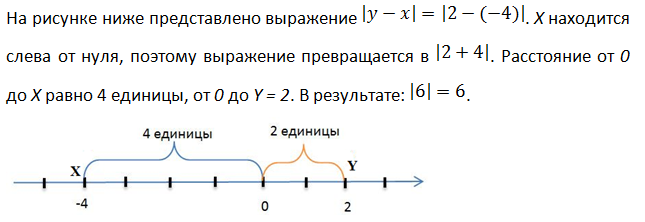
Модуль суммы

Модуль разности

Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

Пример 2.

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

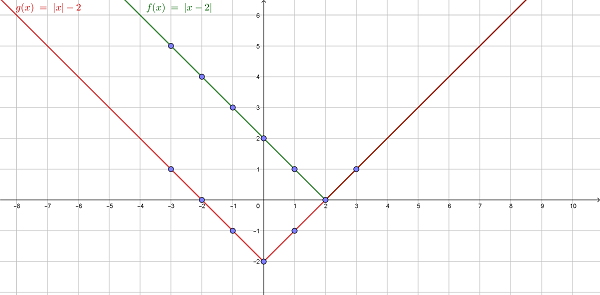
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

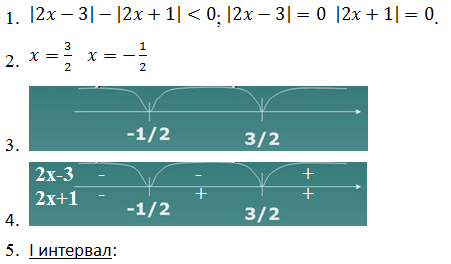
Пример 1. Решить методом интервалов.

Решение:

Результатом будет сумма всех подходящих интервалов.

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:

Далее каждое из равенств разделяется еще на два:

Получено четыре результата:

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

Источник