Что такое обратное отношение
Лекция № 2.. Основные вопросы, рассматриваемые на лекции:



Тема: БИНАРНЫЕ ОТНОШЕНИЯ
Основные вопросы, рассматриваемые на лекции:
1. Декартово произведение множеств.
2. Бинарные отношения.
3. Обратное отношение. Композиция отношений.
4. Отношение эквивалентности и фактор-множество.
5. Отношения порядка.
Краткое содержание лекционного материала
1. Декартово произведение множеств. Упорядоченная пара 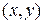
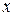
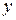
Декартовым произведением 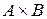
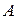
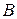
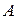
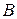
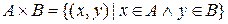
Если 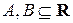
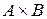
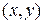
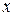
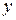
2. Бинарные отношения. Любое подмножество 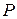
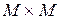
Пусть 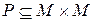
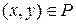
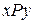
Приведем основные свойства отношения P, заданного на множестве M:
рефлексивность: для всех xÎM выполняется xPx;
антирефлексивность: для всех xÎM неверно, что xPx;
симметричность: для всех x,yÎM из xPy следует, что yPx;
асимметричность: для всех x,yÎM из xPy следует неверно, что yPx;
антисимметричность: для всех x,yÎM из xPy и yPx следует, что x=y;
транзитивность: для всех x,y,zÎM из xPy и yPz следует, что xPz;
3. Обратное отношение. Композиция отношений. Над отношениями, заданными на множестве M, можно производить те же операции, что над множествами: объединение 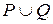
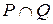
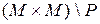
Отношение 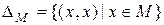
Отношение 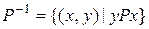
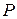
Отношение 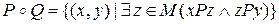
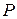
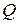
С помощью операций над отношениями можно охарактеризовать свойства отношений: отношение P на множестве M
рефлексивно тогда и только тогда, когда 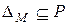
антирефлексивно тогда и только тогда, когда 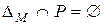
симметрично тогда и только тогда, когда 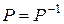
асимметрично тогда и только тогда, когда 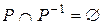
антисимметрично тогда и только тогда, когда 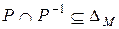
транзитивно тогда и только тогда, когда 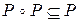
связно тогда и только тогда, когда 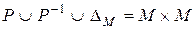
3. Отношение эквивалентности и фактор-множество. Рефлексивное, симметричное и транзитивное отношение называется эквивалентностью.
есть эквивалентность на множестве M, а xÎM. Тогда множество [x]=<y|y
x> называется классом эквивалентности, порожденным элементом x.
Фактор-множество множества 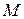
– это семейство всех классов эквивалентности: M/
Семейство множеств Mi, iÎI, называется разбиением M на классы, если:
3) объединение всех Mi, iÎI, совпадает с множеством M.
Теорема 1. Пусть на множестве M задана эквивалентность
. Тогда семейство всех классов эквивалентности [x], xÎM, есть разбиение M на классы.
Теорема 2. Пусть дано разбиение M на классы. Тогда отношение P на M, такое, что xPyÛ»x и y принадлежат одному классу» есть эквивалентность.
Пример. Разбиение множества всех учеников школы на классы определяет эквивалентность «ученики x и y учатся в одном классе».
Функции: обратные отношения и композиции отношений
Функции и бинарные отношения. Рефлексивные, транзитивные и симметричные отношения. Диалектическое и историческое развитие фундаментальных понятий математики. Идея функциональной зависимости в первых математически выраженных соотношениях между величинами.
| Рубрика | Математика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 24.12.2016 |
| Размер файла | 30,5 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
В данной работе мы еще ознакомимся с такими понятиями как обратные отношения и композиции отношений.
Не существует формального определения функции. Понятие функция относится к базовым понятиям математики, и его можно лишь попробовать назвать другим синонимом, например отражение, соответствие, закон или подмножество декартового произведения.
Функцией (отражением, трансформацией) f множества X во множество Y (обозначается f : X >Y) называется такое соответствие между множествами X и Y, которая удовлетворяет следующим условиям:
1. Соответствие f везде определено, то есть, для любого x из X существует такой y из Y, что x f y (y является образом x для функции f), то есть, для любого x из X существует хотя бы один образ y из Y.
2. Соответствие f является соответствием или функциональностью, то есть, если x f y и x f z, то y = z, то есть, y может быть образом сразу нескольких элементов из X, но один элемент x не может порождать больше одного образа из Y.
Элемент y из Y, который отвечает элементу x из X, обозначается как f (x).
Соответствие между X и Y, которая удовлетворяет только условию (1) называется многозначной функцией. Любая функция является многозначной функцией, но не каждая многозначная функция является функцией. Соответствие, которое удовлетворяет только условию (2) есть частичная функция. Любая функция является частичной, но не каждая частичная функция является функцией. Здесь функцией является такое соответствие между множествами, которое удовлетворяет одновременно условиям (1) и (2), если другое не указывается дополнительно.
Для задания отношений можно пользоваться теми же способами, что и при задание множеств. Например, если множество M конечно, то произвольное отношение R на M можно задать списком пар элементов, которые находятся в отношении R.
Удобным способом задання бинарного отношения R на конечном множестве M=
1) рефлексивным, если для всех aєM имеет место aRa.
2) антирефлексивным (иррефлексивным), если ни для одного aєM не выполняется aRa.
3) симметричным, если для всех a, bєM таких, что aRb имеем bRa.
4) асимметричным, если для всех a, bєM таких, что aRb не выполняется bRa.
5) антисимметричным, если для всех a, bєM таких, что aRb и bRa имеем a = b.
6) транзитивным, если из соотношений aRb и bRc выплывает aRc.
7) полным, если для любых a, bєM выплывает, что aRb или bRa.
Обратное отношение и композиция отношений
Обратное отношение имеет такие свойства:
1) Отношение равно своему обратному являются симметричными.
2) Если отношение R имеет такие свойства: рефлексивность, антирефлексивность, симметричность, антисимметричность и транзитивность, то и обратное отношение имеет такие же свойства.
Пример. Пусть А = <1,2,3>, В = <х, у>, а C=
В процессе работы мы узнали, что такое функция, некоторые свойства функций. Так же ознакомились с понятиями: бинарное отношение, обратное отношение, композиция отношений. Наглядные примеры помогли нам лучше усвоить эти понятия.
И напоследок, понятие функции является одним из основных понятий математики вообще. Оно не воз никло сразу в таком виде, как мы им пользуемся сейчас, а как и другие фундаментальные понятия прошло длинный путь диалектического и исторического развития.
Список используемой литературы
1. Евстафьева В.Ю. Математика. Алгебра. Функции. Анализ данных. Москва: «Дрофа», 2000 года.
2. Ильин В.А., Куркина А.В. Высшая математика. Москва: «Проспект», 2003 года.
3.Колмогоров А. Н. Алгебра и начала анализа. Москва: «Просвещение», 1990 года.
4. Максименко В.Н. Математический анализ в примерах и задачах: Часть. 2. Москва: «НГТУ», 2002 года.
5. Никольский С.Н. Курс математического анализа, учебник. Москва: «Физматлит», 2002 года.
Размещено на Allbest.ru
Подобные документы
Отношения зависимости. Произвольные пространства зависимости. Транзитивные и конечномерные пространства зависимости. Существование базиса в транзитивном пространстве зависимости. Связь транзитивных отношений зависимости с операторами замыкания. Матроиды.
дипломная работа [263,2 K], добавлен 27.05.2008
Проведение исследования на уроках обобщающего повторения курса математики в контексте ведущего понятия «порядковая структура». Примеры алгебраических и геометрических бинарных отношений. Включение учащихся в исследовательскую и проектную деятельность.
курсовая работа [1,6 M], добавлен 01.12.2014
Типичные примеры рефлексивных бинарных отношений. Понятие множества и его элементов. Операции над множествами: объединение, пересечение и разность. Декартово произведение множеств. Отношения функциональные, эквивалентности, порядка. Отношения степени n.
контрольная работа [163,2 K], добавлен 08.11.2009
Определение корня первого и второго многочлена, вычисление предела функции. Применение правила Лопиталя (предел отношения функций равен пределу отношения их производных). Пример использования замечательного предела, который применяется в виде равенства.
контрольная работа [95,5 K], добавлен 19.03.2015
Определение, типы и примеры отношений, способы их задания; алгебраическая и геометрическая интерпретации. Разбиение на классы и фактор-множество. Смысл отношения эквивалентности. Теорема о равносильности определений. Отношения в школьной математике.
курсовая работа [1,0 M], добавлен 01.10.2011
Различные трактовки понятия функции в школьном курсе математики. Функция и задание ее аналитическим выражением. Область определения функции и область значений функции. Тесты по теме «Числовые функции. Четные и нечетные функции. Периодические функции».
дипломная работа [213,1 K], добавлен 07.09.2009
Число как одно из основных понятий математики. Виды чисел, абсолютная и переменная величины. Область определения функции, четные и нечетные функции. Построение графиков функций. Пределы последовательности и пределы функции. Непрерывность функции.
учебное пособие [895,7 K], добавлен 09.03.2009
Отношения. Часть I
Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические и информационные объекты, процессы их функционирования. К числу последних я отношу, например, базы данных (реляционные базы данных (РеБД)). Не менее важной считаю область принятия решений, которая состоит из двух основных статистической и алгебраической, основанной целиком на теории отношений. Образовательный уровень специалистов в этой теории близок к нулю.
Откройте учебник по специализации и там увидите в лучшем случае об эквивалентностях, которые авторами трактуются весьма своеобразно. Одного защитившегося уже ДТН спрашиваю: Вы рассматриваете отношение эквивалентности на указывая ни носителя отношения, ни конкретного отношения, как оно у Вас выглядит в записи? Ответ: как выглядит — обыкновенно. Выясняется, что он обо всем этом имеет весьма смутное представление.
Публикаций по проектированию РеБД, кроме иностранных статей назвать затрудняюсь. В 90-х годах был оппонентом, писал отзыв на диссертацию, где рассматривались и иерархические, и сетевые, и реляционные БД. Но как-то год, полтора назад опять на отзыв пришла работа, автор пишет уже только о РеБД, о нормализации отношений БД, но теоретической новизны не показал. Во многих ВУЗах читается курс о базах данных, но не о том, как их создать, создать СУБД, а как правило, о том как эксплуатировать готовую (зарубежную) БД.
Преп. состав не готов научить специалистов IТ-шников создавать отечественные СУБД, ОS, языки программирования, я уж не говорю о БИС, СБИС, заказных БИС. Здесь, по-видимому, поезд ушел давно и надолго. Так что напрасно надуваются у некоторых щеки от гордости (читай снобизма) это видно по комментариям к чужим публикациям, покажите сами, что можете, а не балуйтесь никчемными переводами и перепевками чужого ради предмета гордости — «рейтинга» и «кармы». Сказывается не только отсутствие креатива, но простой образованности и воспитания.
Вторая предметная область неразрывно, связанная с отношениями, — принятие решений. Каждый из нас постоянно занят этим. Мы без решения осознанного или неосознанного пальцем не пошевелим. Мало кто понимает, а еще меньше пишет о решениях. В основе решения любого ЛПР (лица, принимающего решение) лежит предпочтение альтернатив. А моделью предпочтения как раз и является такой тип отношений, который назван «пространством отношений предпочтения». Но кто их изучает. Когда я пришел к «специалисту» по отношениям с вопросом о количестве отношений каждого типа, он не зная ответа, «убил» встречным вопросом, а зачем это Вам?
Понятие отношения
Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров, по-видимому, не приводили.
В моей памяти есть несколько на всю жизнь запомнившихся примеров. Об отображениях и об отношениях. Расскажу вначале об отображениях. Имеется два ведерка с краской. В одном белая в другом — черная. И есть коробка с кубиками (очень много). Грани имеют рельефные номера. Сколькими способами можно раскрасить грани кубиков в два цвета? Ответ неожиданный — столькими, сколько 6-разрядных двоичных чисел, или 2 6 = 64. Поясню подробнее ф: 2→6 отображаются 2 объекта в 6. Каждая строчка таблицы- дискретное отображение фi.
Построим таблицу с 6 колонками и краскам сопоставим число белая — нуль, черная — единица, а граням кубика колонки. Начинаем с того, что все 6 граней белые — это 6-мерный нулевой вектор. Вторая строчка одна грань черная, т. е. младший разряд заполнен 1. и так до исчерпания 6-разрядных двоичных чисел. Кубики ставим в общий длинный ряд. У каждого из них как бы появился номер от 0 до 63.
Теперь отображение наоборот. Пачка листов бумаги (много) и 6 красок (фломастеры).
Фломастерами разного цвета надо пометить обе стороны бумажных листов. Сколько листов потребуется. Ответ f: 6 → 2 или 6 2 =36. Речь идет о произвольных отображениях.
Получили 9 упорядоченных пар элементов из А×А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А×А. Вначале простенький пример.
Подмножества будут содержать из А×А разное количество элементов (пар): одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество (Ø). Сколько же получилось подмножеств? Много, а именно 2 9 = 512 элементов.
Определение. Любое подмножество декартова произведения (у нас квадрата) множества называется отношением. Заметим, в произведении используется одно и то же множество. Если множества разные, возникает не отношение, а соответствие.
Символ отношения ставится слева от элементов R(x, y) или между ними x R y; х, у є А.
Определение Множество всех подмножеств множества А называется булеаном. Наш булеан состоит из 2 |А×А| элементов, здесь|А×А| — мощность множества.
Отношения можно задавать в разном представлении над А=
Рисунок 1.2. а)Матрица 4×4 бинарного отношения б) нумерация клеток Матрицы
Здесь используются номера клеток, заполненные единицами на рис. 1б)
— Векторное представление. Двоичный вектор для представления бинарного отношения формируется из элементов <0,1>следующим образом:
Рассмотренный пример задания отношения в векторной форме будет иметь следующий вид:
— Представление графом. Поставим в соответствие элементам множества
А =
Проведем в графе дугу от (xi) к (xj) тогда и только тогда, когда пара (xi,xj) є R (при i = j дуга (xi,xi) превращается в петлю при вершине (xi). Пример (рис. 1а) представления бинарного отношения A[4×4] графом изображен на рис.2.2.
Рисунок 2.2. Представление отношения ориентированным графом
Каталог бинарных отношений (n = 3)
Большое видится на расстоянии. Чтобы почувствовать отношения их разнообразие, мощность мне пришлось вручную создать каталог бинарных отношений над множеством из 3-х элементов, который включил все (боле 500 отношений) отношения. После этого «дошло» или «зашло»об отношениях.
Очевидно, что в каталог войдут 2 3×3 = 2 9 отношений, и каждое из них снабдим набором присущих им свойств. Ниже (табл. 3) приводится полный список всех 512 отношений над множеством А, |A| = 3, из трех элементов. Приводятся также результаты подсчета количества отношений (табл. 2), представленных сочетаниями номеров клеток декартова квадрата 3×3, различных подклассов для различных значений мощности множества-носителя (n = 3). Для каждого отношения указаны его основные свойства и принадлежность типу (табл. 3). Сокращения, используемые в каталоге раскрываются таблицей 2
Таблица 2. Количественные характеристики каталога при разных n
Сущность производимых операций с отношениями и их технику удобно пояснять на примерах, которые особенно просты и понятны для бинарных отношений. В операциях могут участвовать, два и/или более отношений. Операции, выполняемые над отдельными отношениями – унарные операции. Например, операции обращения (получение обратного) отношения, взятие дополнения, сужение (ограничение) отношения. Как пользоваться каталогом поясним примером примером.
Пример 2. Рассмотрим строку Nпр =14 таблицы каталога. Она имеет вид
Первые 9 символов строки (справа от равенства) — это двоичный вектор, соответствующий сочетанию из 9 по 2, а именно, номер первой клетки (отсчет слева направо) номер 5-й клетки матрицы бинарного отношения, т.е. элементы а1а1= а2а2 =1. Это сочетание имеет порядковый номер Ncч = 4 и сквозной номер Nпр = 14 в списке всех отношений. В остальных позициях этой строки стоят либо нули, либо единицы. Нули свидетельствуют об отсутствии свойства, соответствующего названию колонки нуля, а единицы – наличие такого свойства у рассматриваемого отношения.
Свойства и количественные характеристики отношений
Рассмотрим наиболее важные свойства отношений, которые позволят в дальнейшем выделить типы (классы) отношений, применяющиеся в реляционных базах данных в теории выбора и принятия решений и других приложениях. Далее будем обозначать отношение символом [R,Ω]. R- имя отношения, Ω — множество-носитель отношения.
1. Рефлексивность. Отношение [R,Ω] называется рефлексивным, если каждый элемент множества находится в отношении R сам с собой (рис. 2.3). Граф рефлексивного БО имеет во всех вершинах петли (дуги), а матрица отношения содержит (Е) единичную главную диагональ.
Рисунок 2.3. Рефлексивное отношение
2. Антирефлексивность. Отношение [R,Ω] называется антирефлексивным, если ни один элемент из множества не находится в отношении R сам с собой (рис. 2.4). Антирефлексивные отношения называют строгими.
Рисунок 2.4. Антирефлексивное отношение
3. Частичная рефлексивность. Отношение [R,Ω] называется частично
рефлексивным, если один или более элементов из множества не находится в отношении R сам с собой (рис. 2.5).
4. Симметричность. Отношение [R,Ω] называется симметричным, если вместе с упорядоченной парой (х, у) отношение содержит и упорядоченную пару (у, х) (рис. 2.6).
7. Транзитивность. Отношение [R,Ω] называется транзитивным, если для всяких упорядоченных пар (х, у),(у, z) є R, в отношении R найдется упорядоченная пара (х, z) є R или если R×R⊆R (рис. 2.9).
8. Цикличность. Отношение [R,Ω] называется циклическим, если для его элементов
9. Ацикличность. Отношения, в которых отсутствуют контуры называются, ациклическими. Для ациклических отношений выполняется соотношение R k ∩R = Ø для любого k > 1 (рис. 2.11).
10. Полнота (связность). Отношение [R,Ω] называется полным (связным), если для любых двух элементов (у, z) є Ω один из них находится в отношении с другим (рис 2.12). Линейность. Линейные отношения – это минимально полные отношения.
Рисунок 2.12. Линейное отношение
Итак, нами установлено, что отношения, как математические объекты, обладают определенными свойствами, определение которых приведены ранее. В следующем пункте рассмотрим существо и проявление некоторых свойств:
Количественные соотношения таких дискретных пространств представляют большой как
теоретический, так и практический интерес. Ниже рассматриваются некоторые аспекты количественных характеристик, связанных со свойствами отношений разных типов.
Операции над отношениями
Как и большинстве систем счисления с отношениями выполняются операции:
Выше было введено понятие бинарного отношения, как подмножества упорядоченных пар декартова произведения множеств, а также были рассмотрены свойства отношений. Кроме того, были упомянуты бинарные отношения и матричное представление отношений. Рассмотрим теперь понятие отношения более подробно, кроме того, рассмотрим основные операции бинарных отношений, наиболее важные из всего их множества для отношений.
Для них должны выполняться следующие условия:
Унарные операции над отношениями
9. Двойственное отношение (P d ) к отношению Р – отношение, образованное всеми теми парами, которые принадлежат универсальному отношению и не принадлежат обратному отношению (дополнение к обратному):
Двойственное и обратное отношения в совокупности содержат все пары декартова произведения A×A и не имеют общих пар, они также как и отношения Р и P образуют разбиение A×A
Сужение (РА1). Отношение [R1, A1] называется сужением отношения [R, A] на множество Ω1, если Ω1⊆ Ω и R1=R∩Ω1×Ω1. Отношение РА1 на множестве А1 ⊆ А – отношение РА1 на множестве А1, образованное всеми теми парами, которые принадлежат отношению Р и одновременно входят в состав декартова произведения А1 × А1. Другими словами, РА1 – пересечение отношений Р и А1×А1. Пусть А1 =
Операции, требующие не менее двух отношений – n-арные (n-местные). В таких операциях могут участвовать отношения только одинаковой арности. Примеры таких операций: пересечение, объединение, разность, симметрическая разность отношений и некоторые другие. Если в операции используется более чем два отношения, то она выполняется последовательно для двух первых, а затем для итогового отношения и третьего и т.д.
Иначе говоря, эти операции определены для двух отношений. При операциях над отношениями предполагается, что области задания отношений (операндов и результата) совпадают, арности отношений совпадают, и результатом операции снова является отношение той же арности. В качестве примеров будем рассматривать операции над бинарными отношениями P и Q, заданными на дискретном множестве
А =
1. Пересечение (P ∩ Q) – отношение, образованное всеми теми парами элементов из А, которые входят в оба отношения, т.е. общие для P и Q,
P ∩ Q = <(ai aj) | ((ai aj) є P) & ((ai aj) є Q)>.
Матрица отношения P ∩ Q получается как булево пересечение матриц P и Q:
При отсутствии таких общих пар говорят, что пересечение отношений пусто, т.е. оно является нуль-отношением. Пересечением отношений R1 и R2 (R1∩R2 ) называется отношение, определяемое пересечением соответствующих подмножеств из А×А.
2. Объединение (PUQ). Объединением отношений R1 и R2 (R1UR2 ) называется отношение, определяемое объединением соответствующих подмножеств из А×А. Отношение, образованное всеми парами, составляющими или отношение P, или отношение Q, т.е. парами, принадлежащими хотя бы одному из отношений (связка ∨ — или объединительная)
P U Q = <(ai aj) | ((ai aj) є P) ∨ ( (ai aj) є Q)>.
Если в множестве А×А нет других пар, не вошедших в отношение PUQ, а пересечение их нулевое, то говорят, что отношения P и Q при объединении образуют полное отношение А×А, а их система – разбиение этого полного отношения. Объединение матриц отношений образуется как булева сумма матриц отношений:
3.Разность (P\Q) – отношение, образованное теми парами из Р, которые не входят в отношение Q
P\Q = <(ai aj) | ((ai aj) є P)&((ai aj)∉Q)>.
Разность для отношений в матричном представлении имеет вид
4. Умножение отношений. Упорядоченные пары, образующие отношения могут содержать одинаковые элементы, а могут и не содержать. Среди пар, имеющих в своем составе одинаковые элементы, выделим такие упорядоченные пары, которые назовем смежными (примыкающими) и которые имеют во второй паре 1-й элемент, а в первой паре 2-й элемент один и тот же. Определим произведение смежных пар как упорядоченную пару:
( ai ak)∙( ak aj) => (ai aj).
В терминах теории графов сказанное означает, что смежные пары образуют маршрут из точки (ai) в точку (aj) транзитом через точку (ak), состоящий из 2-х смежных дуг. Произведение этих дуг – третья дуга из точки (ai) в точку (aj), реализующая переход между крайними точками маршрута в том же направлении, минуя промежуточную точку (ak). Говорят, что дуга (ai aj) замыкает эти точки напрямую.
5. Симметрическая разность (P∆Q) – отношение, образованное теми парами, которые входят в объединение PUQ, но не входят в пересечение P∩Q. Другая форма определения объясняет название операции: P∆Q образовано теми упорядоченными парами, которые являются объединением разностей P\Q и Q\P. Таким образом, выражение для симметрической разности записывается двумя разными способами:
P∆ Q = (PU Q)\(P ∩ Q) = (P\Q)U (Q\P).
Матрица симметрической разности имеет вид:
Из последней записи следует, что операция симметрической разности допускает перестановку операндов, т. е. коммутативна.
5. Композиция или произведение (P∙Q) – отношение, образованное всеми парами, для которых выполняется:
P∙Q = <(ai aj)|((ai ak) є P) & ((ak aj) є Q)>.
Другими словами, каждая упорядоченная пара в результирующем отношении есть результат умножения смежных пар, из которых 1-я пара принадлежит первому сомножителю-отношению, 2-я – второму сомножителю-отношению. Операция композиции не коммутативна.
Композиция (Р◦Q) на множестве М – отношение R, заданное на том же множестве М, которое содержит пару (x, y), когда существует Z є M такое, что (x, z) є P и (z, y) є Q.
При матричном представлении отношений матрица композиции отношений равна булеву произведению матриц исходных отношений:
Частный случай композиции отношений – квадрат отношения.
Можно показать, используя индукцию, что n-я степень отношения определяется рекуррентно по формуле:P n =P n-1 ◦Р, это означает, что пара (x,y) є P n в том случае, когда в матрице Р существует цепочка элементов: такая, что (xi, xi+1)є P, 1 Литература





