Что такое несовместные события
1.2.2. Совместные и несовместные события.
Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
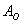
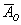
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
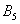
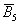
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
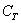
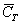
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, 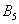
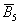
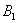
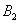
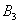
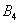
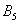
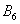
События 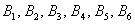
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 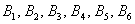
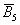
В примере с картами события 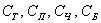
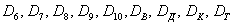
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
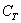
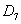
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
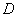
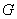
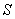
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Теория вероятности. Часть 2
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.
Подборку задач на отработку темы смотрите здесь.
Теоремы сложения и умножения вероятностей
Теорема сложения вероятностей. Теорема умножения вероятностей.
Составитель преподаватель кафедры высшей математики Ищанов Т.Р.
Тeория. Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте; в противном случае события называются совместными.
Пример 1. При бросании игральной кости выпадение 3 очков и 6 очков события несовместные, так как они одновременно не могут произойти в одном и том же опыте.
Пример 2. А — появление четырех очков при бросании игральной кости; В-появление четного числа очков. События А и В совместные, так появление одного из них не исключает появление другого в одном и том же испытании.
Два события называются независимыми, если вероятность появления одного из них не влияет на вероятность появления другого события, в противном случае события зависимы.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С – появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то «АВС» – выпадение «герба» во всех трех испытаниях.
Условной вероятностью 
px;»> 
» alt=»\[P_A (B)=(P(AB))/(P(A))\]» title=»Rendered by QuickLaTeX.com»/>
Пример 3. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).
Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность
px;»> 
» alt=»\[P_A(B)=\frac35.\]» title=»Rendered by QuickLaTeX.com»/>
Этот же результат можно получить по формуле
px;»> 
» alt=»\[P_A(B)=\frac
Действительно, вероятность появления белого шара при первом испытании
px;»> 
» alt=»\[P(A)=\frac36=\frac12.\]» title=»Rendered by QuickLaTeX.com»/>
Найдем вероятность Р (АВ) того, что в первом испытании появится черный шар, а во втором—белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений
Из этого числа исходов событию AВ благоприятствуют 
Искомая условная вероятность
Как видим, получен прежний результат.
Теорема умножения вероятностей (для зависимых событий). Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
px;»> 
» alt=»\[P(AB)=P(A)P_A (B)\]» title=»Rendered by QuickLaTeX.com»/>
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
В частности, для трех событий 
Пример 4. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический.
Решение. Вероятность того, что первый валик окажется конусным (событие А), 
Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик— конусный, т. е. условная вероятность 
По теореме умножения, искомая вероятность
px;»> 
» alt=»\[P(AB)=P(A)P_A(B)=\frac<3><10>\cdot \frac79=\frac<7><30>.\]» title=»Rendered by QuickLaTeX.com»/>
Пример 5. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором — черный (событие В) и при третьем—синий (событие С).
Решение. Вероятность появления белого шара в первом испытании
Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность
Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что в первом испытании появился белый шар, а во втором — черный, т. е. условная вероятность
px;»> 
» alt=»\[P(ABC)=P(A)P_A(B)P_
Теорема умножения вероятностей (для независимых событий). Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то А+В – попадание при первом выстреле, или при втором, или в обоих выстрелах. В частности, если два события А и В – несовместные, то А+В – событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Теорема сложения вероятностей (для несовместных событий). Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Пример 6. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Решение Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие A) P (A) = 10/30 = 1/3. Вероятность появления синего шара (событие B) P (B) = 5/30 = 1/6. События A и B несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 1/3 + 1/6 = 0,5.
Пример 7. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35.Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.
Решение. Событие A – «стрелок попал в первую область» и B – «стрелок попал во вторую область» — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 0,45 + 0,35 = 0,80.
Теорема сложения вероятностей (для совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Для трех событий A, B, C имеем:
Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий:
Пример 8. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: p1 = 0,7; p2 = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события АВ (оба орудия дали попадание) Р (АВ)=Р (А)*Р(В) = 0,7*0,8 = 0,56. Искомая вероятность Р(А+В)=Р(А) + Р(В)—Р(АВ) = 0,7 + 0,8 — 0,56=0,94.
Замечание. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой 
Искомая вероятность того, что при одном залпе хотя бы одно орудие даст попадание, равна 
Для зависимых событий:
Вероятность появления хотя бы одного события.
Частный случай. Если события 
Практический материал.
1.(6.4.12) В урне 4 белых и 3 черных шара. Из нее вынимают 2 шара. Найти вероятность того, что оба шара белые. Рассмотреть выборки: а) без возвращения; б) с возвращением.
2. Вероятность наступления некоторого случайного события в каждом опыте одинакова и равна 0,2. Опыты проводятся последовательно до наступления этого события. Определить вероятность того, что: а) придется проводить четвертый опыт; б) будет проведено четыре опыта. Ответ: а) P (A)=0,8 3 ; б) P (B)=0,8 3 ·0,2
3. Три стрелка одновременно стреляют по одной мишени. Вероятности попадания при одном выстреле соответственно равны 0,7; 0,8 и 0,9. Найти вероятности того, что при одновременном залпе этих стрелков в мишени будет: а) только одно попадание; б) хотя бы одно попадание. Ответ: а) 0,092; б) 0,994
4. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8. (Указание: Задача обратная примеру 8). Ответ: 0,7
5. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное. Ответ: 0,18
6. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность. Ответ: 0,432


















