Что такое неравномерный код

Что такое неравномерный код

При работе с информацией, очень важно передать её в форме, понятной получателю.

Для представления информации в различных формах применяют коды.

| Код – это система условных знаков для представления информации.
qr-коды – удобный способ представлять информацию, которую можно декодировать с помощью смартфона.
| Кодирование – процесс представления информации в форме кода.

Закодированная информация может быть открытой и доступной для всех, в отличии от шифра.

| Шифрование – это процесс, при котором открытый код становится сокрытым.

Для того, чтобы лучше понять разницу между кодом и шифром, рассмотрим несколько примеров.

Шифр «Пляшущие человечки»

Для людей с ограниченными возможностями зрения был разработан специальный способ кодировки – шрифт Брайля. Здесь, каждому символу русского алфавита в соответствие ставится шеститочечный рельефный шрифт. Но при желании, прочитать данную информацию может лю-бой. Такая информация является кодом, но не является шифром.

Шрифт Брайля

Равномерный и неравномерный код

Пример: Дано слово ДАМА. Каждой букве этого слова соответствует уникальный двоичный код:

А	Д	М
000	010	100

Двоичный код этого слова: 010000100000.

Такой код называется равномерным, потому что каждый символ этого слова имеет разный двоичный код одинаковой длины.

| Неравномерный код – это код, в котором каждый символ имеет двоичный код различной длины.

Пример.

А	Д	М
0	1	10

Двоичный код слова ДАМА: 10100.

Очевидно, что при таком способе кодирования сообщение получается короче. Однако, однозначно декодировать такое сообщение будет затруднительно.

| Декодирование – это процесс восстановления исходного сообщения из кода.

Условие Фано

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом другого, более длинного кода.

К уроку:

Источник

Что такое неравномерный код

При работе с информацией, очень важно передать её в форме, понятной получателю.

Для представления информации в различных формах применяют коды.

| Код – это система условных знаков для представления информации.
qr-коды – удобный способ представлять информацию, которую можно декодировать с помощью смартфона.
| Кодирование – процесс представления информации в форме кода.

Закодированная информация может быть открытой и доступной для всех, в отличии от шифра.

| Шифрование – это процесс, при котором открытый код становится сокрытым.

Для того, чтобы лучше понять разницу между кодом и шифром, рассмотрим несколько примеров.

Шифр «Пляшущие человечки»

Для людей с ограниченными возможностями зрения был разработан специальный способ кодировки – шрифт Брайля. Здесь, каждому символу русского алфавита в соответствие ставится шеститочечный рельефный шрифт. Но при желании, прочитать данную информацию может лю-бой. Такая информация является кодом, но не является шифром.

Шрифт Брайля

Равномерный и неравномерный код

Пример: Дано слово ДАМА. Каждой букве этого слова соответствует уникальный двоичный код:

А	Д	М
000	010	100

Двоичный код этого слова: 010000100000.

Такой код называется равномерным, потому что каждый символ этого слова имеет разный двоичный код одинаковой длины.

| Неравномерный код – это код, в котором каждый символ имеет двоичный код различной длины.

Пример.

А	Д	М
0	1	10

Двоичный код слова ДАМА: 10100.

Очевидно, что при таком способе кодирования сообщение получается короче. Однако, однозначно декодировать такое сообщение будет затруднительно.

| Декодирование – это процесс восстановления исходного сообщения из кода.

Условие Фано

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом другого, более длинного кода.

К уроку:

Источник

Что такое неравномерный код

Здравствуйте! Меня зовут Александр Георгиевич. Я являюсь профессиональным репетитором в области информационных технологий, математике, баз данных и программирования.

Если у вас возникли затруднения с обработкой равномерного или неравномерного кода, то срочно записывайтесь ко мне на первый пробный урок, на которых мы с вами очень детально разберем все ваши вопросы и прорешаем большое количество различных тематических упражнений.

Чтобы гарантированно набрать на официальном экзамене ОГЭ или ЕГЭ по информатике высоченный балл берите сотовый телефон, дозванивайтесь до меня и задавайте любые интересующие вопросы.

Рекомендую использовать формат дистанционного обучения! Это выгодно, удобно и эффективно!

Что такое равномерный код и в каких случаях его применяют?

Допустим, вам требуется написать секретное письмо и отправить его своему другу. Вы – человек, проживающий на территории России, следовательно, использующий для написания слов буквы русского алфавита. И, вот, вы решаете закодировать ваше послание двоичным кодом, то есть вместо русских слов ваш друг получит набор цепочек, состоящий из нулей и единиц.

Но ваш соратник без особых проблем сможет провести дешифрацию вашего информационного сообщения, так как вы ему расскажете об алгоритме шифрации/дешифрации.

Символ

Равномерный код

Десятичное представление

Равномерный код – такой код, когда все символы какого-либо алфавита кодируются кодами одинаковой длины.

Что такое неравномерный код и в каких случаях его применяют?

Чтобы глубоко понять смысл неравномерного кодирования давайте представим, что вы работаете на продуктовом складе. Вы хотите оптимизировать свою работу и закодировать название каждого товара минимально возможным количеством бит.

На ум приходит вариант с равномерным кодом, то есть закодировать название каждого продукта информационным кодом одинаковой длины. Но в данном случае это не самый оптимальный вариант кодирования. Почему? Потому что один товар является наиболее популярным и востребованным, и вам, как кладовщику, приходится чаще с ним взаимодействовать.

Следует понять общий принцип неравномерного кода: суть его в том, чтобы кодировать наиболее часто используемые элементы как можно меньшим количеством бит, так как ими вы оперируете очень часто.

Неравномерный код – такой код, когда все элементы какого-либо множества кодируются кодом различной длины.

Данные четыре товара покупают огромными партиями и вы уже устали вести записи в базе данных постоянно вбивая названиях этих продуктов. Давайте применим следующее кодирование:

Итого, нам потребовалось два бита информации, чтобы закодировать в бинарном виде наиболее ходовых четыре товара.

А как поступить с наименее популярными товарами, например, муку и перец также достаточно часто покупают. В этом случае данные товары можно запрограммировать так:

Вы должны уловить общий принцип: чем наименее популярный товар, тем большим количеством бит он будет закодирован.

И все бы хорошо, но есть одна существенная проблема, возникающая при создании неравномерного кода, – проблема с однозначной дешифрацией. Для полного понимания данной проблемы вам следует познакомиться с условием Фано.

Равномерный код vs неравномерный код

Чтобы хорошо понимать в каких ситуациях стоит применять то или иное кодирование, вам нужно очень хорошо разобраться с частотой использования элементов, которые вы планируете закодировать. Если частота применения приблизительно равна у всех элементов, то смело применяйте равномерный код, в других случаях – неравномерный код.

А сейчас я вам предлагаю ознакомиться с мультимедийным решением, в котором я показываю, как правильно оперировать равномерным и неравномерным кодом.

Я хочу записаться к вам на индивидуальный урок по информатике и ИКТ

Если у вас остались какие-либо вопросы по рассматриваемой теме, то записывайтесь ко мне на первый пробный урок. Я репетитор-практик, следовательно, на своих уроках я уделяю максимум внимания решению заданий. Из теории лишь записываются самые базовые сведения: определения, тезисы, формулировки теорем и аксиом.

Специально для своих потенциальных клиентов я разработал стабильную многопараметрическую систему, состоящую из 144 вариантов нашего будущего взаимовыгодного сотрудничества. Даже самый взыскательный клиент сумеет выбрать вариант, полностью покрывающий его запросы.

Не откладывайте свое решение в долгий ящик. Я все-таки достаточно востребованный и квалифицированный репетитор, поэтому звоните прямо сейчас – количество ученических мест ограниченно!

Источник

MT1402: Теоретические основы информатики. Имитационное моделирование

Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды

Как следует из названия, в способах кодировании, относящихся к этой группе, знаки первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Длительности элементарных сигналов при этом одинаковы %%(τ_0 = τ_1 = τ)%%. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время %%K(A,2) \cdot τ%%.

Таким образом, задачу оптимизации неравномерного кодирования можно сформулировать следующим образом: построить такую схему кодирования, в которой суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.

Параллельно должна решаться проблема различимости кодов. Представим, что на выходе кодера получена следующая последовательность элементарных сигналов:

Неравномерный код с разделителем

В соответствии с перечисленными правилами построим кодовую табл. 3.1 для букв русского алфавита, основываясь на приведенных ранее (табл. 2.1.) вероятностях появления отдельных букв.

Теперь можно найти среднюю длину кода К(r,2) для данного способа кодирования:

Поскольку для русского языка, %%I_1(r) = 4,356 бит%%, избыточность данного кода, согласно (3.5), составляет:

это означает, что при данном способе кодирования будет передаваться приблизительно на 14% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение %%К(e,2) = 4,716%%, что при %%I_1(e) = 4,036%% бит приводят к избыточности кода %%Q(e,2) = 0,168%%.

Буква	Код	%%p_j\cdot 10^3%%	%%k_j%%	Буква	Код	%%p_j\cdot 10^3%%	%%k_j%%
пробел	000	174	3	я	1011000	18	7
о	100	90	3	ы	1011100	16	7
е	1000	72	4	з	1101000	16	7
а	1100	62	4	ь,ъ	1101100	14	7
и	10000	62	5	б	1110000	14	7
т	10100	53	5	г	1110100	13	7
н	11000	53	5	ч	1111000	12	7
с	11100	45	5	й	1111100	10	7
р	101000	40	6	х	10101000	9	8
в	101100	38	6	ж	10101100	7	8
л	110000	35	6	ю	10110000	6	8
к	110100	28	6	ш	10110100	6	8
м	111000	26	6	ц	10111000	4	8
д	111100	25	6	щ	10111100	3	8
п	1010000	23	7	э	11010000	3	8
у	1010100	21	7	ф	11010100	2	8

Рассмотрев один из вариантов двоичного неравномерного кодирования, попробуем найти ответы на следующие вопросы: возможно ли такое кодирование без использования разделителя знаков? Существует ли наиболее эффективный (оптимальный) способ неравномерного двоичного кодирования?

Суть первой проблемы состоит в нахождении такого варианта кодирования сообщения, при котором последующее выделение из него каждого отдельного знака (т.е. декодирование) оказывается однозначным без специальных указателей разделения знаков. Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом*) какого-либо иного более длинного кода.

Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой.

Пример.Пусть имеется следующая таблица префиксных кодов:

а	л	м	р	у	ы
10	010	00	11	0110	0111

Требуется декодировать сообщение:

Декодирование производится циклическим повторением следующих действий:

Применение данного алгоритма дает:

шаг	рабочее слово	текущее сообщение	распознанный знак	декодированное сообщение
0	Пусто	0010001000011101010101110000110	—	—
1	0	0100010000111010101110000110	нет	—
2	00	1000100001110101011110000110	м	м
3	1	0001000011101010101110000110	нет	м
4	10	0010000111010101110000110	а	ма
5	0	010000111010101110000110	нет	ма
6	00	10000111010101110000110	м	мам
.

Доведя процедуру до конца, получим сообщение: «мама мыла раму».

Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных. Мы рассмотрим две схемы построения префиксных кодов.

Источник

Мысли вслух

вторник, 23 октября 2012 г.

Ещё раз про однозначное декодирование

Введение

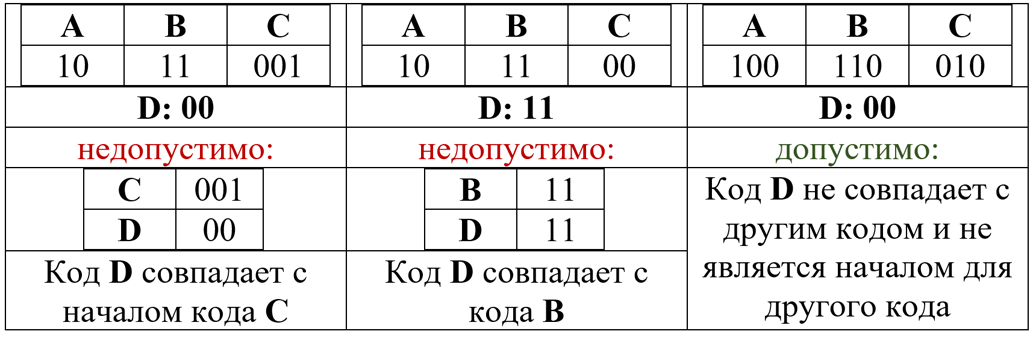
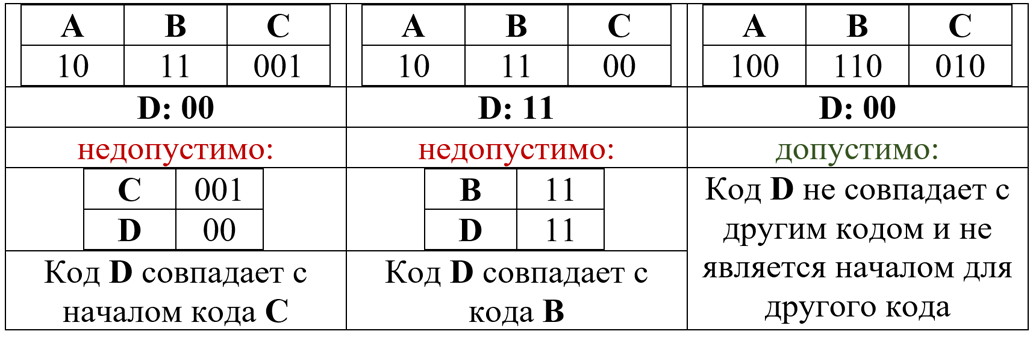
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А — 00, Б — 01, В — 100, Г — 101, Д — 110. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1) для буквы Д — 11; 2) это невозможно; 3) для буквы Г — 10; 4) для буквы Д — 10

Как показывает практика, эта задача вызывает серьезные трудности не только у многих учеников, но даже у учителей информатики.

Нужно сказать, что этот материал практически не рассматривается в существующих школьных учебниках информатики, поэтому все (как ученики, так и учителя) вынуждены разбираться самостоятельно. В то же время вузовские учебники 2, где соответствующая теория изложена строго и научно, достаточно сложны для понимания. Попробуем разобраться в сути кодирования и декодирования на школьном уровне, то есть так, как можно объяснить ученикам 8-11 классов.

В чём проблема?

Предположим, нам нужно передать сообщение по цифровым каналам связи. Для этого его необходимо закодировать, то есть сопоставить каждому символу исходного сообщения некоторый код (кодовое слово). Для определенности будем использовать двоичные коды, то есть последовательности нулей и единиц.

Пример 1. Пусть для кодирования фразы «МАМА МЫЛА ЛАМУ» выбран такой код:

М	А	Ы	Л	У	пробел	(1)
00	1	01	0	10	11

Коды букв «сцепляются» в одну битовую строку и передаются, например, по сети:
Эта цепочка битов приходит в пункт назначения, и тут возникает проблема — как восстановить исходное сообщение (конечно, при условии, что мы знаем код, то есть знаем все пары «символ–кодовое слово», которые использовались при кодировании).

Итак, мы получили 0010011100010111010010. Легко понять, что при использовании кода (1) раскодировать такое сообщение можно самыми разными способами. Например, можно предположить, что оно составлено только из букв А (код 1) и Л (код 0). Тогда получаем
В общем, ни мамы, ни ламы.

Определение. Код называется однозначно декодируемым, если любое кодовое сообщение можно расшифровать единственным способом (однозначно).

Сказанное выше означает, что код (1) НЕ является однозначно декодируемым. Как же определить, является ли заданный код однозначно декодируемым? Этим вопросом мы и займемся.

Равномерные коды

Проблема состоит в том, чтобы правильно разбить полученную битовую цепочку на отдельные кодовые слова. Для того, чтобы её решить, можно, например, использовать равномерный код, то есть код, в котором все кодовые слова имеют одинаковую длину. Например, в нашей фразе 6 символов, поэтому можно использовать 3-битный код (который позволяет закодировать 8 = 2 3 различных символов).

Пример 2. Закодируем фразу из примера 1, используя код:

М	А	Ы	Л	У	пробел	(2)
000	001	010	011	100	101

Получаем закодированное сообщение
Длина этого сообщения — 42 бита вместо 22 в предыдущем варианте, зато его легко разбить на отдельные кодовые слова и раскодировать («_» обозначает пробел):
Видим, что равномерные коды неэкономичны (закодированное сообщение в примере 2 почти в два раза длиннее, чем в примере 1), но зато декодируются однозначно.

Неравномерные коды

Для того, чтобы сократить длину сообщения, можно попробовать применить неравномерный код, то есть код, в котором кодовые слова, соответствующие разным символам исходного алфавита, могут иметь разную длину.

Пример 3. Используем для кодирования фразы из примера 1 следующий код:

М	А	Ы	Л	У	пробел	(3)
01	00	1011	100	1010	11

Получаем
Здесь 34 бита. Это, конечно, не 22, но и не 42.

Несложно показать, что эта битовая цепочка декодируется однозначно. Действительно, первая буква — М (код 01), потому что ни одно другое кодовое слово не начинается с 01. Аналогично определяем, что вторая буква — А. Действительно, за 01 следует 00 (код буквы А) и никакое другое кодовое слово не начинается с 00. Это же свойство, которое называется условием Фано, выполняется не только для кодовых слов 01 и 00, но и кодовых слов всех других букв (проверьте это самостоятельно).

Условие Фано. Никакое кодовое слово не совпадает с началом другого кодового слова.

Коды, для которых выполняется условие Фано, называют префиксными (префикс слова — это его начальный фрагмент). Все сообщения, закодированные с помощью префиксных кодов, декодируются однозначно.
Префиксные коды имеют важное практическое значение — они позволяют декодировать символы полученного сообщение по мере его получения, не дожидаясь, пока всё сообщение будет доставлено получателю.

Упражнение. Расшифруйте сообщение, закодированное кодом (3). При расшифровке кода очередной буквы не заглядывайте вперёд!
Термины «условие Фано» и «префиксный код» не используются в заданиях ЕГЭ и ГИА, однако для решения этих задача важно, чтобы ученики понимали содержание условия Фано.

Пример 4. Рассмотрим ещё один код

М	А	Ы	Л	У	пробел	(4)
10	00	1101	001	0101	11

Ясно, что он не является префиксным: код буквы А (00) совпадает с началом кода буквы Л (001) и код пробела (11) совпадает с началом кода буквы Ы (11). Закодированное сообщение
также имеет длину 34 бита, как и при использовании кода (3). Начнем раскодировать с начала. Ясно, что первой стоит буква М, потому что ни один другой код не начинается с 10. Затем — комбинация 001, которая может быть кодом буквы Л или кодом буквы А (00), за которым следует код буквы Ы или пробела. Получается, что для декодирования сообщения нам нужно «заглядывать вперёд», что очень неудобно.

Попробуем декодировать с конца битовой строки. Последние биты 0101 могут представлять только букву У, следующие 10 — только букву М и т.д. Можно проверить, что теперь сообщение однозначно декодируется с конца! Это происходит потому, что выполняется условие, которое можно назвать «обратным» условием Фано: никакое кодовое слово не совпадает с окончанием другого кодового слова. Коды, для которых выполняется обратное условие Фано, называют постфиксными (постфикс или суффикс слова — это его конечный фрагмент). В этом случае тоже обеспечивается однозначное декодирование. Таким образом,

Сообщение декодируется однозначно, если для используемого кода выполняется прямое или обратное условие Фано.

Однозначно декодируемые коды

Пример 5. Рассмотрим код, предназначенный для кодирования сообщений, состоящих только из букв А, Б и В:

А	Б	В	(5)
0	11	010

Так как код буквы А (0) совпадает как с началом, так и с концом кода буквы В (010), для этого кода не выполняются ни прямое, ни обратное условие Фано. Поэтому пока мы не можем с уверенностью сказать, декодируется ли он однозначно.

Закодируем сообщение
и попытаемся раскодировать эту строку, используя код (5). В первую очередь, замечаем, что две соседние единицы могут появиться только при использовании буквы Б (код 11), поэтому сразу выделяем две таких группы:
Здесь жёлтым фоном выделена уже декодированная часть сообщения. В оставшейся части единица может появиться только в коде буквы В (010), в битовой строке находим две такие группы:
Оставшиеся нули — это коды букв А. Анализ алгоритма показывает, что такой код всегда однозначно декодируется.

Полный ответ на вопрос об однозначной декодируемости получил в начале 1960-х годов советский математик Ал.А. Марков, предложивший решение с помощью графов [2]. Продемонстрируем его метод на примере.

Пример 6. Рассмотрим код

А	Б	В	Г	Д	(6)
01	010	011	11	101

Здесь не выполняется ни «прямое», ни «обратное» условие Фано, поэтому возможно, что декодировать сообщение однозначно не удастся. Но утверждать это заранее нельзя.

Код является однозначно декодируемым тогда и только тогда, когда в построенном таким образом графе нет ориентированных циклов, включающих вершину Λ.

Таким образом, код (6) не обладает свойством однозначной декодируемости.

Проверим таким же способом код (5), который, как мы уже выяснили, не является ни префиксным, ни постфиксным. Множество последовательностей, которые совпадают с началом и концом кодовых слов, состоит из пустой строки и единицы: <Λ, 1>. Граф, построенный с помощью приведённого выше алгоритма, содержит два узла и одну петлю:

В этом графе нет цикла, содержащего вершину Λ, поэтому любое сообщение, записанное с помощью такого кода, декодируется однозначно. Выше мы показали это с помощью простых рассуждений.

Нужно отметить, что на практике применяются, главным образом, префиксные коды, поскольку они позволяют декодировать сообщение по мере его получения, не дожидаясь окончания приёма данных.

Ещё примеры

Пример 7. Рассмотрим задачу А9 из демо-варианта КИМ ЕГЭ-2013 [1], которая сформулирована в начале статьи. Нужно оптимизировать код
выбрав один из вариантов
Решение. Сначала давайте посмотрим на исходный код, приведённый в условии. Можно заметить, что он префиксный — для него выполняется условие Фано: ни один из трехбитных кодов не начинается ни с 00 (код А), ни с 01 (код Б). Поэтому сообщения, закодированные с помощью такого кода, декодируются однозначно.

Заметим, что «обратное» условие Фано не выполняется: код буквы А (00) совпадает с окончанием кода буквы В (100), а код буквы Б (01) совпадает с окончанием кода буквы Г (101).

Теперь проверим, что получится, если сократить код буквы Д до 11 (вариант 1). Свойство однозначной декодируемости может быть потеряно только тогда, когда в результате такого сокращения нарушится условие Фано, то есть код буквы Д совпадёт с началом какого-то другого кодового слова. Видим, что этого не произошло — нет других кодовых слов, которые начинаются с 11, поэтому вариант 1 — это и есть верное решение.

Остается убедиться, что варианты 3 и 4 не подходят. Если мы сократим код буквы Г до 10 (вариант 3), условие Фано оказывается нарушенным, так как теперь код буквы Г (10) совпал с началом кода буквы В (100). Одновременно нарушено и «обратное» условие Фано: код буквы А (00) совпадает с окончанием кода буквы В (100). Но, как мы знаем, при этом код может всё-таки быть однозначно декодируемым.

Конечно, можно построить граф, как было сделано выше, и проверить, есть ли в нём циклы, включающие вершину Λ. В данном случае граф выглядит так:

Построение и анализ графа — дело достаточно трудоемкое и требующее аккуратности. Обычно в таких случаях значительно легче просто подобрать последовательность, которая может быть декодирована двумя разными способами.

Наконец, нужно убедиться, что вариант 4 не удовлетворяет условию. Если мы сократим код буквы Д до 10, условие Фано оказывается нарушенным, так как теперь код буквы Д (10) совпал с началом кода буквы В (100). Как и раньше, нарушено «обратное» условие Фано: код буквы А (00) совпадает с окончанием кода буквы В (100) и код буквы Б (01) совпадает с окончанием кода буквы Г (101).

Построим граф по методу Ал.А. Маркова:

Пример 8. Оптимизируйте код
сохранив свойство однозначной декодируемости сообщений. Выберите один из вариантов:
Решение. Определим, за счёт чего обеспечивается однозначная декодируемость исходного кода. Легко видеть, что код префиксный — для него выполняется условие Фано: ни одно из трёхбитовых кодовых слов не начинается ни с 11 (код А), ни с 10 (код Б). В то же время, обратное условие Фано не выполняется, потому что код буквы А (11) совпадает с окончанием кода буквы В (011).

Проверим вариант 1 — сократим код буквы Г до 00. При этом нарушилось условие Фано, которое обеспечивало однозначную декодируемость исходного варианта: теперь код буквы Г (00) совпадает с началом кода буквы Д (001). Но и обратное условие Фано тоже не выполняется для пары букв А-В. Поэтому можно предположить, что такой код не обладает свойством однозначной декодируемости. И действительно, легко находится цепочка 001011, которую можно раскодировать как ГБА (00 10 11) или ДВ (001 011).

Рассмотрим вариант 3 — сократим код буквы В до 01. При этом условие Фано выполняется, поскольку ни одно из кодовых слов не начинается с 01, то есть код является префиксным и однозначно раскодируется. Это и есть правильный ответ.

На всякий случай проверяем вариант 4 — сокращает код буквы Б до 1. При этом код перестает быть префиксным, и обратное условие Фано также не выполнено (код буквы Б совпадает с началом и концом кода буквы А). Сразу понятно, что последовательность 11 можно раскодировать как А или как ББ, поэтому этот вариант неверный.

Выводы

В заметке выполнен подробный анализ задачи на кодирование, которая предлагается на ЕГЭ в последние несколько лет. Нужно заметить, что в нём затрагивается вузовский курс дискретной математики. Понятно, что нельзя требовать от школьников знания теорем Ал.А. Маркова об однозначном декодировании, но учителю полезно более глубоко представлять себе эти вопросы, которые можно разбирать на факультативах. В качестве дополнительной литературы по этой теме можно рекомендовать 4.

С точки зрения практического подхода, для решения всех известных автору реальных задач подобного типа достаточно найти вариант, при котором выполняется условие Фано или обратное условие Фано (одно из двух!).

Литература

Комментарии: 16:

Спасибо, что «на пальцах» объяснили еще раз!

Действительно, спасибо. Очень понятно.

Просто великолепная статья!
Спасибо!

Уважаемый Константин! Бесконечно благодарна Вам за неоценимую помощь в подготовке детей к ЕГЭ по информатике.

Спасибо), всё понятно)))

Отличная статья! Спасибо!

Спасибо за статью. В учебнике информатики 10 класса Полякова содержится опечатка в последовательности построения графа Маркова, которая, при всей схожести текста, исправлена у вас. Порадовало также более ясное объяснение примеров.

> В учебнике информатики 10 класса Полякова содержится опечатка
Да, действительно была в первом издании. Сейчас исправлена.

Программа, скачанная отсюда, на codeTable = выдала следующий список вершин графа: [‘Lambda’, ‘0’, ‘1’].
Но разве ‘2’ не должна входит в список вершни, так как является началом ‘E’ и концом ‘C’ и не является кодовым словом?

> Но разве ‘2’ не должна входит в список вершин, так как является началом
> ‘E’ и концом ‘C’ и не является кодовым словом?
Программа предназначена только для обработки двоичных кодов.

А как можно доказать на пальцах, что из отсутствия данного граф-цикла следует однозначность декодируемости? А то зашел в учебник Маркова, а там просто жесть какая-то. Развитие моего ума не позволяет мне это изучить в разумные сроки.

Последний граф для кода А — 00, Б — 01, В — 100, Г — 101, Д — 10 составлен не совсем точно.
Нужно еще из вершины Λ в вершину 1 провести дугу Д → Г.

Подпишитесь на каналы Комментарии к сообщению [Atom]

Константин Поляков Санкт-Петербург

Источник