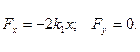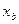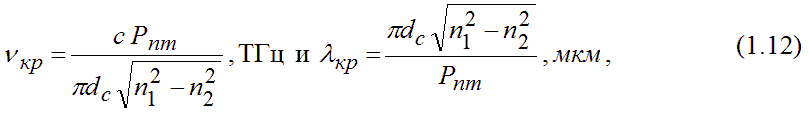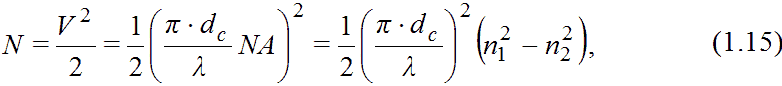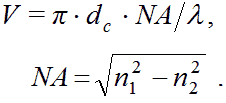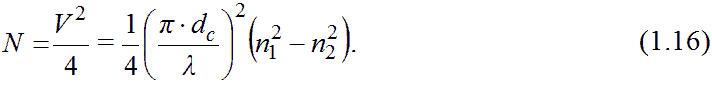Что такое мода колебаний

Нормальные моды колебаний

Системы с двумя степенями свободы

Особый интерес представляет случай, когда одна колеблющаяся система связана с другой системой, которая тоже может колебаться. В этом случае для каждого из осцилляторов можно записать свое уравнение динамики, эти уравнения в общем случае не являются независимыми. Каждый осциллятор имеет свою частоту, амплитуду и фазу, т.е. система обладает двумя степенями свободы.

Такие системы называются связанными. Простой пример связи – два маятника, соединённые нитью, к середине которой подвешен груз Р (рис.1.1.14). При помощи силы, действующей на нить, маятник А связан с маятником В. Если маятник В во время колебания удалится от А, то сила связи между этими маятниками становится больше, а при сближении – меньше. Маятник А получает в такт с колебаниями маятника В импульс периодически действующей силы, частота которой согласуется с частотой собственных колебаний А, но может отличаться от частоты колебаний В.

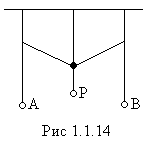
Под влиянием силы связи между маятниками разной длины маятник А приходит в колебательное движение. Когда маятник В колеблется, его амплитуда возрастает с каждым новым импульсом, в то время, как амплитуда В убывает. Спустя известное время, амплитуды маятника А убывают, а маятника В возрастают до тех пор, пока не наступит обратное явление. Таком образом, энергия колебаний передаётся через связь от одной колеблющейся системы другой и обратно.

Если периоды собственных колебаний обоих маятников равны, то обмен энергией осуществляется нацело.

Из эксперимента известно, что процесс передачи энергии между маятниками идёт тем быстрее, чем больше масса груза Р. Если два маятника колеблются с одинаковыми периодами, амплитудами и фазами колебаний, то никакого обмена энергией между ними не происходит. Должна быть разница в амплитудах или фазах колебаний, чтобы энергия была получена или отдана.

В общем случае движение системы с двумя степенями свободы может иметь очень сложный вид, не похожий на простое гармоническое движение.

Можно показать, что для двух степеней свободы и при линейных уравнениях движения наиболее общее движение является суперпозицией двух независимых простых гармонических движений, происходящих одновременно. Эти два простых гармонических движения называются нормальными или собственными колебаниями или гармониками, а так же нормальными модами колебаний или просто модами. Создавая определённые начальные условия (определённые начальные значения xa, xbи dxa/dt, dxb/dt) можно создать систему, колебания которой соответствуют только одной из мод.

Нормальные колебания (нормальные моды) – это собственные (свободные) гармонические колебания линейных динамических систем с постоянными параметрами, в которых отсутствуют как потери, так и приток извне колебательной энергии. Каждое нормальное колебание характеризуется определенным значением частоты, с которой осциллируют все элементы системы, и формой — распределением амплитуд и фаз по элементам системы. Линейно независимые нормальные колебания, отличающиеся формой, но имеющие одну и ту же частоту, называются вырожденными. Частоты нормальных колебаний называются собственными частотами системы.

В дискретных системах, состоящих из N связанных гармонических осцилляторов (например, механических маятников, колебательных контуров), число нормальных колебаний равно N. В распределённых системах (струна, мембрана, резонатор) существует бесконечное, но счётное множество нормальных колебаний. Произвольное свободное движение колебательной системы может быть представлено в виде суперпозиции нормальных колебаний. При этом полная энергия движения распадается на сумму парциальных энергий, отдельных нормальных колебаний. Таким образом, линейная система ведёт себя, как набор независимых гармонических осцилляторов, которые могут быть выбраны в качестве обобщённых нормальных координат, описывающих движение в целом. Однако в динамических системах могут существовать и собственные движения, не сводящиеся к нормальным колебаниям (равномерные вращения, постоянные токи и др.).

При внешнем возбуждении системы нормальные колебания в значительной мере определяют её резонансные свойства. Резонанс может возникнуть лишь в том случае, когда частота гармонического внешнего воздействия близка к одной из собственных частот системы либо к их линейной комбинации, если внешнее воздействие меняет параметры системы (параметрический резонанс). При этом важным оказывается также и пространственное распределение воздействия — максимальный эффект достигается при соблюдении не только временного, но и «пространственного синхронизма».

В линейных системах с переменными параметрами при выполнении определенных условий также возможно представление движений в виде суперпозиции нормальных колебаний, отличающихся, однако, от гармонических. Понятие нормальных колебаний может быть приближённо распространено на системы, содержащие неконсервативные и нелинейные элементы, если их воздействие приводит к медленным изменениям амплитуд и фаз квазигармонических нормальных колебаний (в масштабе периода самих нормальных колебаний или периода биений между ними).

Свойства мод. Если существует лишь одна мода колебаний, то в системе совершается простое гармоническое движение. Все части системы колеблются с одной частотой, одновременно проходя через положение равновесия (для которого х=0). Например, движения или не могут соответствовать одной моде, так как в первом случае различны фазовые постоянные, во втором – частоты.

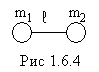
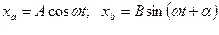
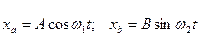
Рассмотрим моду, движение которой описывается уравнением

. (1.6.1)

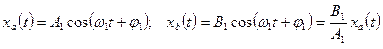
назовем ее мода 1. Из уравнения движения видно, что у обеих степеней свободы одна и та же частота и фаза. Для моды 2 получаем

. (1.6.2)

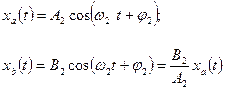
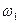
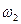
Каждая мода имеет свою собственную частоту: для моды 1 и для моды 2.

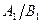
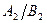
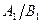
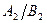
Для каждой моды система имеет характерную “конфигурацию” или “форму”, определяемую отношением амплитуд движений по двум направлениям: для моды 1 и для моды 2. Для данной моды отношение xa/xbпостоянно и не зависит от времени, оно определяется в нашем случае отношением или , которые могут быть либо положительными, либо отрицательными.

Наиболее общим движением является суперпозиция, при которой движение содержит обе моды колебаний одновременно:

. (1.6.3)

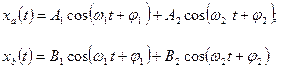
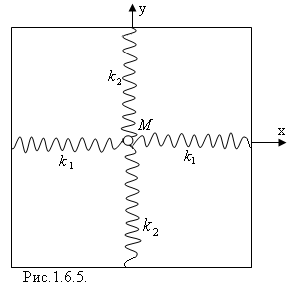
В качестве примера рассмотрим двумерный гармонический осциллятор (рис.1.6.5). Масса М, укреплённая на двух парах взаимно перпендикулярных пружин, может свободно двигаться в плоскости ХУ. В направлении оси Х она соединена со стенками двумя невесомыми пружинами с коэффициентами жёсткости , а в направлении У – двумя другими невесомыми пружинами с коэффициентом жёсткости . В случае малых колебаний x-компонента возвращающей силы полностью обусловлена пружинами , а у-составляющая возвращающей силы зависит только от пружин . В положении равновесия система имеет вид, представленный на рис.1.6.5. Сообщим массе М небольшое смещение х в направлении +х, тогда возвращающая сила станет равна

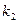
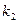
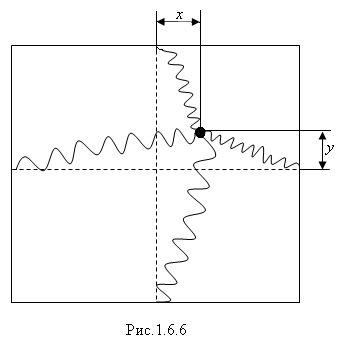
Теперь из этого положения дадим массе небольшое смещение у в направлении +у. Нужно выяснить, изменилось ли значение .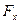

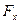
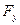
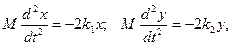
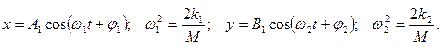
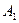
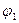
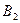
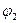
Тогда можно считать, что величина не изменилась, то же можно сказать и о . Мы получили два линейных уравнения: решения которых

(1.6.4)

Из этих уравнений следует, что движения в направлениях Х и У не связаны между собой, и каждое движение представляет собой гармоническое колебание с собственной частотой. Движение вдоль оси Х соответствует одной нормальной моде колебаний, а вдоль оси У – другой моде. Колебания вдоль оси Х (1 мода) имеют амплитуду и фазу , которая зависит только от начальных условий х(0) и х‘(0), то есть от смещения и скорости в момент времени t=0. Аналогично, для колебаний вдоль оси У (2 мода) амплитуда и фаза зависят только от начальных значений у(0) и у‘(0).

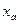
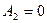
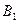
Нормальные координаты. Естественный выбор координат х и у вдоль осей пружин дал нам независимые уравнения (1.6.4), каждое из которых соответствует одной моде. С точки зрения общих решений (1.6.3) это эквивалентно тому, что в выражении для амплитуда , а для =0. Столь удачно выбранные нами координаты х и у называются нормальными координатами. Рассмотрим систему координат х‘у’, которая связана с ху поворотом на угол α.

В большинстве задач, содержащих системы с двумя степенями свободы, не так легко «на глаз» найти нормальные координаты. Как правило, уравнения движения для систем с двумя степенями свободы – это два связанных уравнения. Один из методов решения таких связанных дифференциальных уравнений – это поиск новых переменных, которые являлись бы линейной комбинацией первоначальных, неудачно выбранных координат и которые давали бы не связанные, а разделённые уравнения движения. Такие новые координаты называются нормальными.

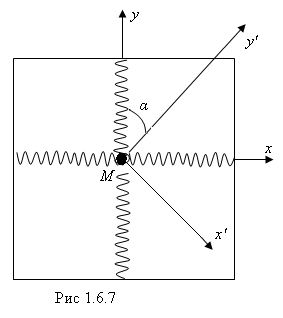
В нашем примере для получения нормальных координат нам нужно повернуть оси х’ и у’ на угол α до совпадения их с осями х и у.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

МОДА (тип колебаний)

Смотреть что такое «МОДА (тип колебаний)» в других словарях:

тип колебаний — virpesių moda statusas T sritis radioelektronika atitikmenys: angl. oscillation mode vok. Schwingungsart, f; Schwingungsmode, f rus. вид колебаний, m; мода колебаний, f; тип колебаний, m pranc. mode d oscillations, m … Radioelektronikos terminų žodynas

тип колебаний — svyravimų tipas statusas T sritis fizika atitikmenys: angl. mode of oscillation; mode of vibration vok. Schwingungsart, f; Schwingungstyp, m rus. мода колебаний, f; тип колебаний, m pranc. mode d’oscillations, m; type d’oscillations, m … Fizikos terminų žodynas

независимый тип колебаний — nesusietoji moda statusas T sritis radioelektronika atitikmenys: angl. uncoupled mode vok. ungekoppelte Schwingungsart, f rus. независимый тип колебаний, m; несвязанная мода, f pranc. mode pur, m … Radioelektronikos terminų žodynas

вырожденный тип колебаний — išsigimusioji moda statusas T sritis fizika atitikmenys: angl. degenerate mode vok. Ausartungsmodus, m; entarteter Wellentyp, m rus. вырожденная мода, f; вырожденный тип колебаний, m pranc. mode dégénéré, m … Fizikos terminų žodynas

МОДА — тип колебаний (нормальные колебания) в распределенных колебательных системах или тип волн (нормальные волны) в волноводных системах и волновых пучках (см. Волновод, Квазиоптика). Термин мода стал употребляться также для любого волнового поля (вне … Большой Энциклопедический словарь

МОДА — тип колебаний (нормальные колебания) в распределённых колебат. системах или тип волн (нормальные волны) в волноводных системах и волновых пучках. Термин М. стал употребляться также для любого волнового поля (вне его источников), обладающего оп… … Естествознание. Энциклопедический словарь

мода — ы; ж. [франц. mode мода; манера, образ действий] 1. Совокупность вкусов и взглядов, господствующих в обществе в определённое (обычно недолгое) время и проявляющихся в увлечениях чем л., формах быта, одежде и т.п. М. на высокие каблуки. Выйти из… … Энциклопедический словарь

мода колебаний — virpesių moda statusas T sritis radioelektronika atitikmenys: angl. oscillation mode vok. Schwingungsart, f; Schwingungsmode, f rus. вид колебаний, m; мода колебаний, f; тип колебаний, m pranc. mode d oscillations, m … Radioelektronikos terminų žodynas

мода колебаний — svyravimų tipas statusas T sritis fizika atitikmenys: angl. mode of oscillation; mode of vibration vok. Schwingungsart, f; Schwingungstyp, m rus. мода колебаний, f; тип колебаний, m pranc. mode d’oscillations, m; type d’oscillations, m … Fizikos terminų žodynas

МОДА — (фр.). Временный условный обычай в обществе, выражающийся в покрое одежды, в нарядах, в нравах. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. МОДА господство в данное время каких либо вкусов, направлений и т. п … Словарь иностранных слов русского языка

Источник

Собственная мода

Собственные частоты системы зависят от ее геометрии, структуры и свойств материала. Собственные частоты струны музыкального инструмента определяются, например, ее длиной, материалом и натяжением. То же касается всех вибрационных систем.

Оглавление

теория

Уравнения движения системы получаются из уравнений Лагранжа

Подход к решению уравнения:

(Положительные) корни корней многочлена

Таким образом, общее решение системы уравнений колебаний системы является суперпозицией ее собственных колебаний и, возможно, равномерного движения.

Нормальные координаты

а знак равно ( А. я ( k ) ) <\ displaystyle a = \ left (> ^ <(k)>\ right)>

так что для всех собственных значений, которые не являются вырожденными, все недиагональные элементы должны равняться нулю. Соответствующая нормировка собственных векторов приводит к соотношению ортонормированности а Т Т а <\ displaystyle a ^ <\ mathrm> Ta>

а Т Т а знак равно 1 <\ displaystyle a ^ <\ mathrm> Ta = 1>

написано так, что утверждение следует непосредственно умножением на слева. а Т <\ Displaystyle а ^ <\ mathrm>>

Примеры

Пружинный маятник

с полиномом первой степени от ω 2 <\ displaystyle \ omega ^ <2>>

и собственный вектор

Молекула CO ₂

для определителя системы

Включены три его нуля

а собственные векторы равны

Это тоже дает общее решение

Вибрирующая струна

Вибрирующая струна имеет бесконечное количество степеней свободы и, соответственно, бесконечное количество собственных частот. Однако они должны соответствовать граничным условиям задачи. Волновое уравнение является

должен быть. Это приводит к граничному условию

а общее решение волнового уравнения представляет собой суперпозицию по всем собственным колебаниям:

Нормальные колебания молекул

Квантовая механика

является. Если оператор Гамильтона не зависит от времени, то существует формальное решение уравнения Шредингера

Источник

Большая Энциклопедия Нефти и Газа

Каждая мода колебания на грани z 0 представляется членом вида amw cos kmx-cos knv, причем частота о одинакова для всех мод колебания в данной задаче. [4]

Эти моды колебаний ( фононы) обладают свойствами, аналогичными фотонному газу. Напротив, при больших температурах возбуждаются все возможные моды колебаний. [5]

Каждая мода колебаний распространяется в данной пластине с определенной фазовой скоростью. Необходимым условием распространения волн Лэмба является параллельность акустических границ контролируемого изделия. [6]

Рассмотрим поперечную электромагнитную моду колебания в изотропной плазме. [8]

Для случая трехкратно вырожденной моды колебаний ( волновые функции задаются выражением (7.10.207)) можно дать явное вычисление амплитуды перехода. Хотя это вычисление является частным случаем соотношения (7.10.345), мы повторяем его с целью непосредственной иллюстрации привлекаемых понятий теории углового момента. [10]

Энергию на моду колебаний можно получить, разделив (4.67) на число стоячих волн ( см. § 1 гл. [11]

Возникновение той или иной моды колебаний зависит от материала пластины, ее толщины и частоты возбуждающих колебаний. [13]

В табл. IL2 приведены моды колебаний для некоторых молекул. [14]

В многоатомных молекулах число возможных мод колебаний тем выше, чем больше число атомов в молекуле, причем кроме колебаний, обусловленных деформацией и изгибом, становятся возможными крутильные колебания вокруг некоторых связей. [15]

Источник

1.3. СВОЙСТВА СВЕТОВОДА, ОСНОВАННЫЕ НА ЗАКОНАХ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

1.3.1 Волновая трактовка световых процессов. Классы волн

Волны подразделяются на классы и типы.
На уровне электромагнитного взаимодействия с молекулами учитывается явление электрической поляризации, пространственные электрические E и магнитные H поля. Они допускают колебания соответствующих векторов (E, H) только в определённых плоскостях.
Волноведущую систему можно представить идеальным цилиндром с продольной осью z, а оси x и y образуют поперечную (xy), горизонтальную (xz) и вертикальную (yz) плоскости. В этой системе выделяют 4 класса волн по признаку отсутствия либо наличия продольных составляющих E_z и H_z (рисунок 1.7).

Следует обратить внимание на то, что термин «электрическая волна» не означает, что существует лишь электрическое поле и лишь вектор напряжённости электрического поля. В этой волне, как и во всех направляемых волнах, существует электромагнитное поле, т.е. обязательно электрический и магнитный векторы.

1.3.2 Типы волн (моды)

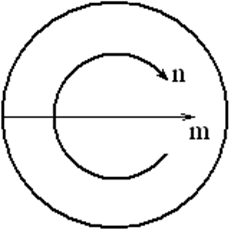
Рисунок 1.8 – Пояснение к понятию «тип волны»

Оказывается, что в ВС существуют только два типа волн HE_nm и EH_nm.
При n=0 имеем симметричные моды E_0m и H_0m.
При n≥1 имеем несимметричные (гибридные) моды HE_nm и EH_nm.
Часть внеапертурных лучей распространяется в оболочке, соответствующие им моды называют оболочечными. Они играют определённую роль в улучшении характеристик световодов. Чем меньше диаметр сердцевины d_c, тем меньше сечение светового потока, поступающего в оптическое волокно, тем меньше различных типов колебаний (обусловленных множеством решений уравнений Максвелла), или мод, возникает в нём.
В ОМ волоконом световоде поддерживается только одна гибридная мода HE₁₁, называемая основной модой. В ММ волоконном световоде поддерживаются различные, как гибридные моды так и Е- и Н- моды.
Не все моды указанных наборов можно реализовать. Чтобы понять, какие моды могут возникнуть, нужно провести достаточно сложный и кропотливый анализ. Сопоставляя волновую теорию с геометрической оптикой, следует отметить, что симметричные моды E_0m и H_0m соответствуют меридиональным лучам, несимметричные (смешанные) моды HE_nm и EH_nm – косым лучам.

1.3.3 Структура поля

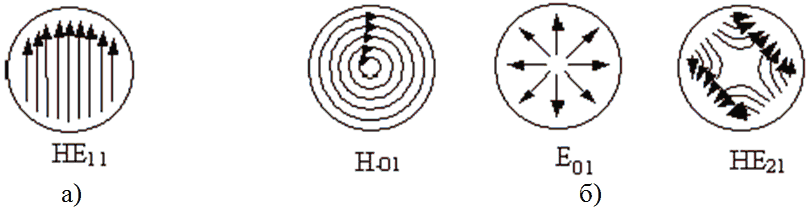
Как мы убедились, вдоль круглого неоднородного диэлектрического световода с осесимметричным распределением &#949 в сердцевине возможно распространение дискретного числа различных по структуре поля типов колебаний (мод) (рисунок 1.9).

а – мода самого низкого порядка; б – первый ряд мод более высоких порядков
Рисунок 1.9 – Картины векторов поперечного электрического поля в поперечном сечении сердцевины ступенчатого волоконного световода для четырёх мод самых низких порядков

Они отличаются кроме числа вариаций поля по азимуту и радиусу ещё и соотношением между продольными компонентами E_z и H_z.

1.3.4 Оптические параметры световода

Основными электродинамическими характеристиками регулярного световода при небольшом числе распространяющихся мод являются:

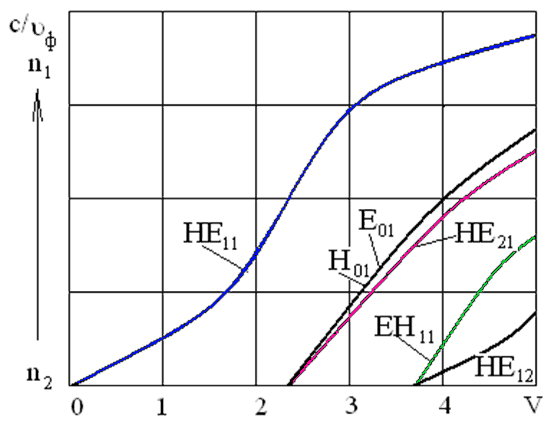
Рисунок 1.10 – Дисперсионные характеристики ступенчатого волоконного световода для нескольких первых мод

Эти дисперсионные характеристики начинаются при с/υ_ф=n₂.
С увеличением V; фазовые скорости уменьшаются, но всегда находятся в пределах:

Равенство с/υ_ф=n₂ представляет собой условие частоты отсечки V_отс.
Частота отсечки – предельная частота, ниже которой невозможно возникновение моды с определёнными индексами. Точки на оси абсцисс, в которых начинаются дисперсионные кривые, соответствуют критическим значениям нормированной частоты V.
Нормированную частоту отсечки V_отс также называют нормированной критической частотой V_kp. На частоте отсечки поле выходит из сердцевины в оболочку и мода исчезает.
Направляемую волну, имеющую наименьшую критическую частоту в данной среде распространения, называют основной волной.
В волоконном световоде для основной волны НЕ₁₁ V_kp=0.
Для основной волны может быть реализован одноволновый или одномодовый режим в пределах от критической частоты основного типа до критической частоты волны ближайшего типа.
Если на заданной рабочей частоте параметры световода выбрать так, чтобы следующие высшие моды Е₀₁, H₀₁, HЕ₂₁ с более высокими частотами отсечки не могли распространяться, то получим одномодовый световод, т.е. световод с одной только распространяющейся модой HЕ₁₁. В этом случае должно выполняться условие одномодовости для двухслойного световода. Расчёт на основе уравнений Максвелла и рисунок 1.10 позволяют найти простой критерий распространения одной наинизшей моды: