Что такое минуты в геометрии
Что значит минуты в геометрии?
Минута в геометрии,что это?
в геометрии минутами и секундами измеряется угол,это дробная часть 60 секунд это минута, 60 минут это один градус. а отмечаются они апострофами, один апостроф- минута, два- секунда
Это деления градусов, например как во времени есть час минута секунда, там есть угол градус минута, это используется и в определении координат местонахождения на земле
Вообразите циферблат часов. Полный круг образует 360 градусов. Это если брать часовую стрелку. А можно взять еще минутную, которая образует 60 минут. А еще есть секундная, делящая минуты.
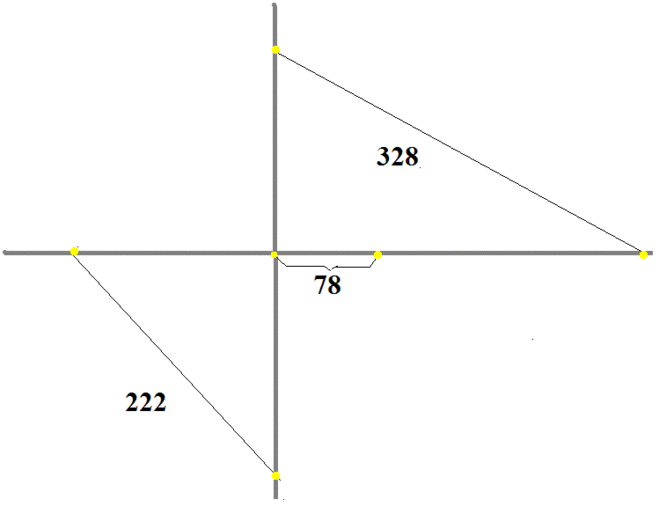
Параметров свободных очень много. Можно выбирать любые. Выберем банальное перпендикулярное пересечение.
Второе и третье подставляем в первое
(78+145V)^2 + (145U)^2 = 328^2
отсюда выражаем U через V
подставляем в четвёртое
V =46,153845 км/час = 0,76923075 км/мин (приблизительно)
Соответственно U =1,84615386 км/мин = 110,7692315862 км/час
Осталась мелочь: догадаться, что нужно поменять, чтобы автомобили достигли перекрёстка одновременно?
Проще всего поменять скорость самих автомобилей и время, через которое состоится встреча, оставив неизменным угол между дорогами и начальные координаты автомобилей.
Попросим автомобили встретиться через час.
За этот час они сблизятся на 328 км. Надо полагать, что скорость сближения 328 км/час
А если попросим встретиться через два часа?
Тогда скорость сближения будет ровно в два раза меньше.
Можно оставить в покое скорости автомобилей, но дать им другие точки старта,
время встречи возьмём из условия через 2 ч 25 мин
Для автомобиля, который и так через это время будет на перекрёстке, ничего менять не будем.
Ну, а второй передвинем влево на 78 км. x = 111,53845875 км
Расстояние между автомобилями s = sqrt(x^2+y^2)=290 км
скорость сближения 290/145 = 2 км/мин = 120 км/час
Но нарушено условие про начальное расстояние между автомобилями.
Сохраним начальное расстояние между автомобилями, но не будем обращать внимания на промежуточное время.
(Ut)^2 + (Vt)^2 = 328^2 => t = 328/sqrt(U^2 + V^2) =164 минуты.
скорость сближения 290/145 = 2 км/мин = 120 км/час
Общее время автопробега 265 мин, после встречи 101 мин. Конечное расстояние
(101/60) * sqrt( U^2 + V^2 )=222 км
С некоторой попытки угадалось, какое число из условия можно выбросить, а какие нельзя.
Какому-то древнему греку взбрело в голову померять землю, а так как землю древние греки обзывали «гео», то измерение земли назвали геометрией. Сначала меряли плоские структуры, выводили законы и зависимости геометрии, потом распространили в третье измерение. Евклид собрал все эти достижения в своей книге «Начала», котрая стала учебником «евклидовой геометрии». В 17 веке Декарт придумал координаты и заложил основы аналитической геометрии. Уже не надо было чертить, стало можно считать пользуясь отношением координат точек примитивов.
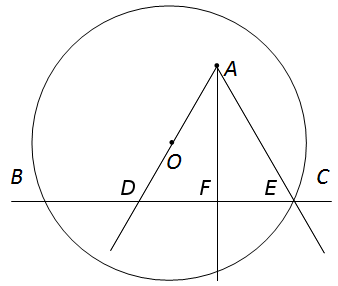
Если линейка градуированная, то окружность не нужна для ответа на вопрос.
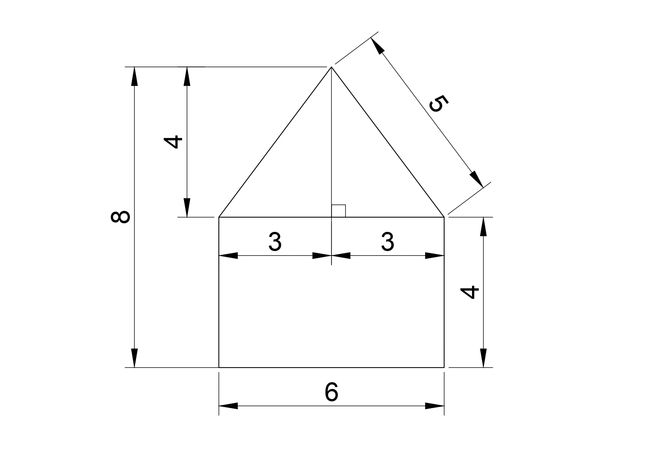
Бытует мнение, что ход решение может быть следующим: «Крыша дома» является равнобедренным треугольником, разделив его высотой получим два прямоугольных треугольника с гипотенузой раной «5» и одним из катетов равным «3» (половина от «6»).
По теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы. Исходя из этого получаем 52=32+х2. Далее следует х2=25-9=16. Второй катет равен «4». Высота стены равна «4» к которой прибавляем «катет». ИТОГО: «8»
Пусть дан произвольный треугольник АВС. Теорема косинусов устанавливает связь между длинами сторон и углами треугольника. Сформулируем:
Квадрат любой стороны в треугольнике равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Сформулируем в частном виде для одной из сторон:
Очень удобная вещь, когда требуется найти угол, зная стороны, или наоборот.
Градусы и минуты в геометрии – Сколько минут в градусе?
Градус (геометрия) — это… Что такое Градус (геометрия)?
Градус, минута, секунда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности.
Градус
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Деление окружности на 360° придумали аккадцы (вавилоняне).
Минуты и секунды
По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается знаком ′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается знаком ″). Корни такого деления лежат в Древнем Вавилоне, где использовалась шестидесятеричная система счисления.
Угловая секунда
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с ). Соотношение между этими величинами определяется формулой 1 c = 15″. [3]
Дольные единицы
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ.
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.
Примечания
Литература
См. также
Измерение градуса угла
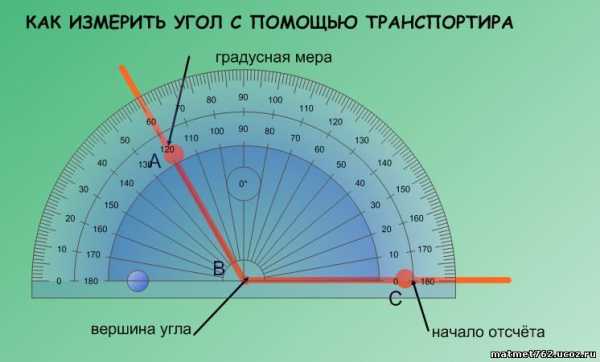
Один градус равен 1/180 от развернутого угла (прямой линии) (что прекрасно видно на транспортире).
Чем меньше угол, тем меньше в нем градусов, соответственно, чем больше угол, тем в нем градусов больше.
Значения углов можно складывать.
Градус можно разделить еще на 60, тогда получаются минуты, которые обозначаются так: «′».
Если разделить и минуты на 60, то получаются секунды, которые обозначают так: «″»
Например, 35 градусов, 27 минут и 14 секунд будут обозначены так: 35°27′14″
Есть несколько удобных и всеми понятных обозначений углов:
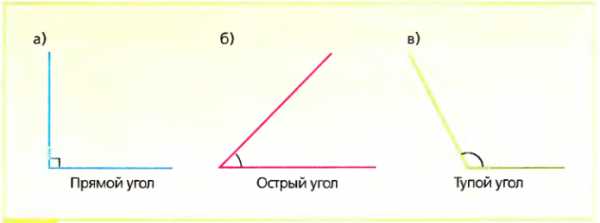
Угол равный 180° называется развернутый;
Угол равный 90°
Угол меньше 90° называется острый;
Угол больше 90° называется тупой.
Кстати, обратите внимание, как много прямых углов вокруг вас.
Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно
Добавить новость и получить деньги
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
Градус (геометрия) — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Градус.
Градус, минута, секунда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, в том числе для определения азимута.
Градус
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.
Градус в альтернативных единицах измерения:
1^\circ = \frac<2 \pi><\displaystyle<360^\circ>> = \frac<\pi><\displaystyle<180^\circ>> радиан = \frac<1^\circ><\displaystyle
Минуты и секунды
По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается знаком x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается знаком y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением в три штриха — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей [5] ; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).
Минуты и секунды в других системах измерения:
rad (1 минута в радианах) 1 = \frac<2\pi> <\displaystyle<360^\circ>\times 60′ \times 60> = \frac<1>
rad (1 секунда в радианах).
Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.
Угловая секунда
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается s ). Соотношение между этими величинами определяется формулой 1 s = 15″. [8]
Дольные единицы
| единица | величина | обозначение | аббревиатура | радиан (прибл.) |
|---|---|---|---|---|
| градус | 1/360 окружности | ° | deg | 17,4532925 mrad |
| минута | 1/60 градуса | ′ | arcmin, amin, \hat <‘>, MOA | 290,8882087 µrad |
| секунда | 1/60 минуты | ″ | arcsec | 4,8481368 µrad |
| миллисекунда | 1/1000 секунды | mas | 4,8481368 nrad | |
| микросекунда | 1 × 10 −6 секунды | μas | 4,8481368 prad |
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.К:Википедия:Статьи без источников (тип: не указан) [источник не указан 2537 дней]
Напишите отзыв о статье «Градус (геометрия)»
Примечания
Литература
См. также
Отрывок, характеризующий Градус (геометрия)
Х
Вернувшись к караулке, Петя застал Денисова в сенях. Денисов в волнении, беспокойстве и досаде на себя, что отпустил Петю, ожидал его.
Что такое минута?
Когда человечество поняло, что можно создать устройства, способные измерять время более точно, чем могли это сделать, например, солнечные часы, то возник простой термин «минута» как мера отрезка времени. Однако используется это слово и в математике, где минутой измеряют углы. Также термин применяется и в других областях.
Разберемся в том, что такое минута и где этот термин применяется сегодня.
Минута как мера времени
Самое популярное и известное повсеместно значение термина «минута» связано с измерением времени. В часе шестьдесят минут, а минута состоит из шестидесяти секунд. Так намного проще измерять время. Минута не является единицей общепринятой системы СИ, однако используется совместно с ней.
Само слово «минута» латинского происхождения и означает «малость, наименьшее, минимум». Раньше считали, что час разделен на «шестьдесят малостей». Поэтому фразу «подожди минуту» можно перевести как «подожди еще малость».
Минута всегда используется для определения хода времени. Также ее можно часто найти в измерениях скорости, где она обозначает время, за которое объект проходит определенное расстояние.
Минута как единица измерения угла
В геометрии углы измеряют градусами, минутами и секундами. По аналогии с минутой, которая делит час, минута в геометрии также делит градус на шестьдесят частей. А сама минута также делится на шестьдесят секунд.
В геометрии минуты и секунды имеют очень малое применение. В основном они используются для перевода градуса в меньшее число для решения уравнений.
Минута также является мерой измерения телесных углов. Тогда ее называют квадратной минутой.
В плоских же углах метрической минутой называют часть измерительной единицы «град». В одном граде 100 метрических минут, а в одной метрической минуте 100 метрических секунд. Метрическую минуту иногда еще называют «сантиград». В настоящее время метрические минуты, секунды и град используются редко. Иногда их закладывают в математическое программное обеспечение и калькуляторы.
Минута в географии
В географии и навигации используется понятие минуты для нахождения точных координат места на карте планеты или местности. Таким образом на море и суше можно найти нахождение необходимого места или узнать, где вы сами находитесь. Сегодня используется в навигаторах и имеет огромное значение для точности.
Географические координаты строятся по принципу сферических. Для определения широты и долготы используются минуты, секунды и градусы. Однако в современном мире чаще используют запись градусов в виде десятичной дроби и иногда в градусах с минутами с десятичной дробью. Полную запись в градусах, минутах и секундах использовали в древности.
Минута как расстояние
Чтобы определять расстояние между звездами и планетами, была придумана новая единица – световой год. Световой год обозначает расстояние, которое свет преодолел за год в полном вакууме, не испытывая влияние гравитации. Данная единица не ис
Градус (геометрия) Википедия
Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
Градус[ | ]
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.
Градус в альтернативных единицах измерения:
У меня есть вопрос по предмету геометрия…
1 градус это 1\180 часть развернутого угла развернутый угол ———А———стороны противонаправлены градус делится на 60 минут, минута обозначается одной черточкой справа наверху минута делится на 60 секунд и обозначается двумя черточками там же.
это минуты. единица измерения углов, меньшая чем градусы. в одном градусе вроде бы 60 минут) на уроках учителя внимательно слушать надо)))))
1° = 60′ — один градус равен шестидесяти минутам 1′ = 60» одна минута равно шестидесяти секундам То, что было написано выше — 135 градусов и 47 минут.
Разворот в один градус можно обозначить как: 1° или 0° 60′ или 0° 0′ 3600». Разворот в половину градуса можно обозначить как: 0,5° или 0° 30′ или 0° 0′ 1800». Расшифровка: Градус, Минута, Секунда. В градусе 60 минут, в минуте 60 секунд.
Градусы и минуты в геометрии — Минуты и секунды в геометрии — 22 ответа
Градусы и секунды
Ответ от 22 ответа[гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Минуты и секунды в геометрии
Ответ от Naumenko[гуру]
градус делится на более мелкие части: 60 минут и каждая минута на 60 секунд по аналогии с временными мерами.
Ответ от Аэростатика[мастер]
Ну…. я точно не помню, но вроде в 1 градусе 60 минут, а в 1 минуте 60 секунд. Вроде бы. Просто это более точное деление градуса. Например, это надо для географии, чтобы более точно отметить точку на карте
Ответ от Вровень[гуру]
Измерение углов.
Ответ от ☺Сашко Чорний☺[гуру]
А еще расстояние может измеряться световыми годами. Кашмарррр!
Ответ от Павел Воронин[гуру]
или это можно записать как 60,53805(5)
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Градус геометрия на Википедии
Посмотрите статью на википедии про Градус геометрия
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Градус – угол, равный одной сто восьмидесятой части развернутого угла.
Градусная мера угла – положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Стороны угла – лучи, из которых состоит угол.
Вершина угла – общее начало сторон угла.
Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
Теоретический материал для самостоятельного изучения.
Ранее вы уже познакомились с геометрической фигурой – уголи его составными элементами.
Сегодня мы продолжим изучать углы, познакомимся с их классификацией и будем измерять углы с помощью транспортира.
Измерение углов аналогично измерению отрезков – оно основано на сравнении, только отрезки сравнивались с отрезком, принятым за единицу измерения, а углы с углом, тоже принятым за единицу измерения.
Обычно за единицу измерения углов принимают градус.
Градус – угол, равный 1/180 части развёрнутого угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу, называется градусной мерой угла.
Для измерения углов используют транспортир. Вспомним, как проводить измерение углов с помощью транспортира.
Транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах на той же шкале.
Но обычно говорят кратко – угол О равен 50 градусам.
Если масштабныйугол не укладываетсяцелое число раз в измеряемом угле, тоединицу измерения делят ещё на части.
Определённые части градуса носят специальные названия.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Далее, аналогично понятию равные отрезки, ведём понятие равные углы.
Дваугла считаются равными, если градус и его части укладываются в этих углах одинаковое число раз, т.е. равные углы имеют равные градусные меры.
Если один угол меньше другого, то градус в нём (или его часть) укладываются в этом углу меньшее число раз, чем в другом, т.е. меньший угол имеет меньшую градусную меру.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Далее рассмотрим классификацию углов.
Мы уже знаем, что есть развёрнутый угол, его градусная мера сто восемьдесят градусов.
Но есть и другие углы.
Например, прямой угол, его градусная мера девяносто градусов;
острый угол, его градусная мера меньше девяноста градусов;
тупой угол, его градусная мера больше девяноста градусов, но меньше ста восьмидесяти.
Выполним практическое задание – построим биссектрису угла с помощью транспортира.
Мы знаем, что биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
OL – биссектриса ∠АОС.
Поэтому для начала определим градусную меру ∠АОС, она составляет 128°, тогда биссектриса этого угла, исходя из определения, составит 64 °.
Итак, сегодня получили представление о том, как измерять и изображать угол с помощью транспортира. Перейдем к практическим заданиям.
Способы измерения на местности.
Измерение углов на местности проводят с помощью различных приборов. Один из таких – астролябия, она состоит из диска (лимб), разбитого на градусы и вращающейся вокруг центра диска линейки (алидады). На концах алидады есть окошечки, которые нужны, чтобы устанавливать её в определённом направлении.
Опишем, как происходит измерение углов с помощью этого прибора. При измерении углов астролябию устанавливают в его вершине, например, точке О, при этом лимб должен находится горизонтально плоскости угла, а отвес, в центе диска, совпадать с вершиной угла.
Затем устанавливаем алидаду вдоль одной из сторон угла, например, АО, отмечаем деление, напротив которого находится указатель алидады.
Далее поворачиваем алидаду по часовой стрелке, пока она не совпадёт со второй стороной угла, у нас это сторона ОВ, отмечаем деление, напротив которого оказался указатель алидады. Теперь можно найти градусную меру измеряемого угла, как разность второго и первого измерения.
1. Луч ВК делит развернутый ∠ОВС на два угла, разность которых равна 56°. Найдите образовавшиеся углы.
Решение: нарисуем рисунок, исходя из условия задачи.
Обозначим ∠СВК за х, тогда ∠ОВК= х + 56°, исходя из условия задачи (разность углов равна 56°). Развёрнутый угол равен 180°. Составим уравнение и решим его.
Тогда ∠ОВК= х + 56°= 62° +56° = 118°.
Ответ: ∠СВК = 62°; ∠ОВК = 118°.
2. Чему равен ∠ЕОА, если ∠ВОА = 130° 54´, а ∠ВОЕ = 105° 76´?
Решение: Найдём ∠ЕОА = ∠ВОА – ∠ВОЕ, т.к. ОЕ – луч, проведённый из вершины ∠ВОА и делящий этот угол на 2 части. Подставим в выражение градусные меры углов и найдём градусную меру ∠ЕОА. Так как в градусе 60 минут, то 105° 76´ = 106° 16´.