Что такое методическая погрешность

Методические погрешности измерений примеры

Возникновение методических погрешностей связано с несовершенством выбранного метода измерений, неточностью эмпирических формул, которые применяются для описания конкретного явления, лежащего в основе измерений и ограниченной точности констант, используемых в уравнениях.

Содержание:

Что относится к погрешности измерений

К методическим также относятся погрешности, которые обусловлены принятыми упрощениями и допущениями при измерении некой модели, в сравнении с реальным объектом.

В одних случаях принятые допущения не оказывают значительного влияния на измерения, в других же влияние может быть существенным.

Погрешность при взвешивание

Примером такой погрешности, которая обусловлена методом измерения, является взвешивание, точнее пренебрежение массой воздуха при взвешивании, который вытесняется гирей, согласно закону Архимеда. Пренебрежение массой воздуха при проведении рабочих взвешиваний вполне допустимо. При точных измерениях, ее необходимо учитывать, внося поправки в конечный результат.

Погрешность при измерение объема тела

Еще один пример: при измерении объема тел, их форму считают геометрически правильной. Но при точных измерениях пренебрегать отклонениями размеров от геометрически правильных нельзя, поэтому недостаточно измерений длины, ширины и высоты для определения объема куба. Необходимо их измерить по всем граням.

Всем методам измерений, которые основаны на данных опытов, присущи погрешности подобного рода. К примеру, методы, используемые для определения твердости металлов.

Погрешности при определение твердости тела

Измерение погрешностей приемом рандомазации

Чаще всего, оценки погрешностей физических констант и формул известны. В противном случае, они переводятся в разряд случайных, и вычисляются с использованием приема рандомизации, т.е. измерение различными методами одной величины и нахождении ее средневзвешенного значения.

Отличие от аналитических измерений от методических

Отличие аналитических измерений в том, что они сопровождаются отбором проб анализируемого образца, ее отправкой в лабораторию для проведения измерений, хранением последующим, подготовкой взятой пробы к инструментальным операциям: очистке, сушке, переводу в иное фазовое состояние и пр., приготовлением растворов калибровочных.

И все это множество операций не учитывается при проведении измерений, что не дает действительного результата проведенных измерений.

Источник

Погрешность измерений

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

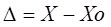
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

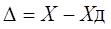
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

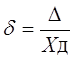
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

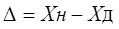
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

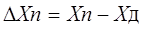
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

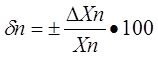
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

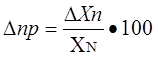
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Источник

Классификация. Погрешность измерений

Эффективность использования измерительной информации зависит от точности измерений — свойства, отражающего близость результатов измерений к истинным значениям измеренных величин. Точность измерений может быть большей или меньшей, в зависимости от выделенных ресурсов (затрат на средства измерений, проведение измерений, стабилизацию внешних условий и т. д.). Очевидно, что она должна быть оптимальной: достаточной для выполнения поставленной задачи, но не более, ибо дальнейшее повышение точности приведет к неоправданным финансовым затратам. Поэтому наряду с точностью часто употребляют понятие достоверность результатов измерений, под которой понимают то, что результаты измерений имеют точность, достаточную для решения поставленной задачи (погрешность измерений).

Классический подход к оцениванию точности измерений, впервые примененный великим математиком Карлом Гауссом и затем развитый многими поколениями математиков и метрологов, может быть представлен в виде следующей последовательности утверждений.

1. Целью измерения является нахождение истинного значения величины — значения, которое идеальным образом характеризовало бы в качественном и количественном отношении измеряемую величину. Однако истинное значение величины найти в принципе невозможно. Но не потому, что оно не существует — любая физическая величина, присущая конкретному объекту материального мира, имеет вполне определенный размер, отношение которого к единице является истинным значением этой величины. Это означает всего лишь непознаваемость истинного значения величины, в гносеологическом смысле являющегося аналогом абсолютной истины. Хорошим примером, подтверждающим это положение, являются фундаментальные физические константы (ФФК).

Они измеряются наиболее авторитетными научными лабораториями мира с наивысшей точностью, и затем результаты, полученные разными лабораториями, согласуются между собой. При этом согласованные значения ФФК устанавливают с таким количеством значащих цифр, чтобы при следующем уточнении изменение произошло в последней значащей цифре. Таким образом, истинные значения ФФК неизвестны, но каждое следующее уточнение приближает значение этой константы, принятое мировым сообществом, к ее истинному значению.

I la практике вместо истинного значения используют действительное значение величины — значение величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.

2. Отклонение результата измерения X от истинного значения Хи (действительного значения Хд) величины называется погрешностью измерений

(2.1)

Вследствие несовершенства применяемых методов и средств измерений, нестабильности условий измерений и других причин результат каждого измерения отягощен погрешностью. Но, так как Хи и Хд неизвестны, погрешность ΔX также остается неизвестной. Она является случайной величиной и поэтому в лучшем случае может быть только оценена по правилам математической статистики. Это должно быть сделано обязательно, поскольку результат измерения без указания оценки его погрешности не имеет практической ценности.

3. Используя различные процедуры оценивания, находят интервальную оценку погрешности ΔX, в виде которой чаще всего выступают доверительные границы — ,+ погрешности измерений при заданной вероятности Р. Под ними понимают верхнюю и нижнюю границы интервала, в котором с заданной вероятностью Р находится погрешность измерений ΔX.

4. Из предыдущего факта следует, что

истинное значение измеряемой величины находится с вероятностью Р в интервале [X— ; Х + ]. Границы этого интервала называются доверительными границами результата измерений.

Таким образом, в результате измерения находят не истинное (или действительное) значение измеряемой величины, а оценку этого значения в виде границ интервала, в котором оно находится с заданной вероятностью.

Погрешности измерений могут быть классифицированы по различным признакам.

1. По способу выражения их делят на абсолютные и относительные погрешности измерений.

Таким образом, относительная погрешность измерения— отношение абсолютной погрешности измерения к истинному значению измеряемой величины или результату измерений.

Для характеристики точности СИ часто применяют понятие «приведенная погрешность», определяемое формулой

Таким образом, приведенная погрешность средства измерения — отношение абсолютной погрешности средства измерения в данной точке диапазона СИ к нормирующему значению этого диапазона.

2. По источнику возникновения погрешности измерений делят на инструментальные, методические и субъективные.

Инструментальная погрешность измерения — составляющая погрешности измерения, обусловленная несовершенством применяемого СИ: отличием реальной функции преобразования прибора от его калибровочной зависимости, неустранимыми шумами в измерительной цепи, запаздыванием измерительного сигнала при его прохождении в СИ, внутренним сопротивлением СИ и др. Инструментальная погрешность измерений разделяется на основную (погрешность измерений при применении СИ в нормальных условиях) и дополнительную (составляющая погрешности измерений, возникающая вследствие отклонения какой-либо из влияющих величин от ее номинального значения или ее выхода за пределы нормальной области значений). Метод их оценивания будет рассмотрен ниже.

Методическая погрешность измерений — составляющая погрещности измерений, обусловленная несовершенством метода измерений. К ней относят погрешности, обусловленные отличием принятой модели объекта измерения от реального объекта, несовершенством способа воплощения принципа измерений, неточностью формул, применяемых при нахождении результата измерений, и другими факторами, не связанными со свойствами СИ. Примерами методических погрешностей измерений являются:

• погрешности изготовления цилиндрического тела (отличие от идеального круга) при измерении его диаметра;

• несовершенство определения диаметра круглого тела как среднего из значений диаметра в двух его заранее выбранных перпендикулярных плоскостях;

• погрешность измерений вследствие кусочно-линейной аппроксимации нелинейной калибровочной зависимости СИ при вычислении результата измерений;

• погрешность статического косвенного метода измерений массы нефтепродукта в резервуаре вследствие неравномерности плотности нефтепродукта по высоте резервуара.

Субъективная (личная) погрешность измерения — составляющим погрешности измерения, обусловленная индивидуальными особенностями оператора, т. е. погрешность отсчета оператором показаний по шкалам СИ. Они вызываются состоянием оператора, несовершенством органов чувств, эргономическими свойствами СИ. Характеристики субъективной погрешности измерений определяют с учетом способности «среднего оператора» к интерполяции в пределах цены деления шкалы измерительного прибора. Наиболее известная и простая оценка этой погрешности — ее максимальное возможное значение в виде половины цены деления шкалы.

3. По характеру проявления разделяют систематические, случайные и грубые погрешности.

Грубой погрешностью измерений (промахом) называют погрешность измерения, существенно превышающую ожидаему при данных условиях погрешность. Они возникают, как правило из-за ошибок или неправильных действий оператора (неверный отсчет, ошибка в записях или вычислениях, неправильное включение СИ и др.). Возможной причиной промаха могут быть сбои работе технических средств, а также кратковременные резкие из менения условий измерений. Естественно, что грубые погрешности должны быть обнаружены и исключены из ряда измерений.

Более содержательно деление на систематические и случайные погрешности.

Систематическая погрешность измерения — составляющая погрешности измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной и той же величины. Систематические погрешности подлежат исключению насколько возможно, тем или иным способом. Наиболее известный из них — введение поправок на известные систематически погрешности. Однако полностью исключить систематическую погрешность практически невозможно, и какая-то ее небольшая часть остается и в исправленном (введением поправок) результате измерений. Эти остатки называются неисключенной систематической погрешностью (НСП). НСП — погрешность измерений, обусловленная погрешностями вычисления и введения поправок или же систематической погрешностью, на действие которой по правка не введена.

Например, с целью исключения систематической погрешности, измерения, обусловленной нестабильностью функции npeoбpaзования аналитического прибора, периодически проводят его калибровку по эталонным мерам (поверочным газовым смесям или стандартным образцам). Однако, несмотря на это, в момент измерения все равно будет некоторое отклонение действительной функции преобразования прибора от калибровочной зависимости, обусловленное погрешностью калибровки и дрейфом функции преобразования прибора за время, прошедшее после калибровки. Погрешность измерения, обусловленная этим отклонением, является НСП.

Случайной погрешностью измерения называется составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же шпчины. Причины случайных погрешностей многообразны: шумы измерительного прибора, вариация его показаний, случайные колебания параметров электрической сети и условий измерений, погрешности округления отсчетов и многие другие. В появлении таких погрешностей не наблюдается какой-либо закономерности, они проявляются при повторных измерениях одной и той же величины в виде разброса результатов измерений. Поэтому оценивание случайных погрешностей измерений возможно только на основе математической статистики (эта математическая дисциплина родилась как наука о методах обработки рядов измерений, отягощенных случайными погрешностями).

В отличие от систематических, случайные погрешности нельзя исключить из результатов измерений путем введения поправок, однако их влияние можно существенно уменьшить проведением многократных измерений.

Источник

Погрешность измерений. Классификация

Погрешность средств измерения и результатов измерения.

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Инструментальные и методические погрешности.

Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Систематическая и случайная погрешности.

Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Причинами возникновения систематических составляющих погрешности измерения являются:

Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.

Погрешности адекватности и градуировки.

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

Абсолютная, относительная и приведенная погрешности.

Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.

Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.

Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

Аддитивные и мультипликативные погрешности.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).

Источник