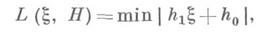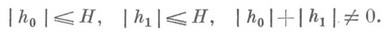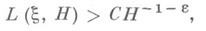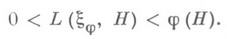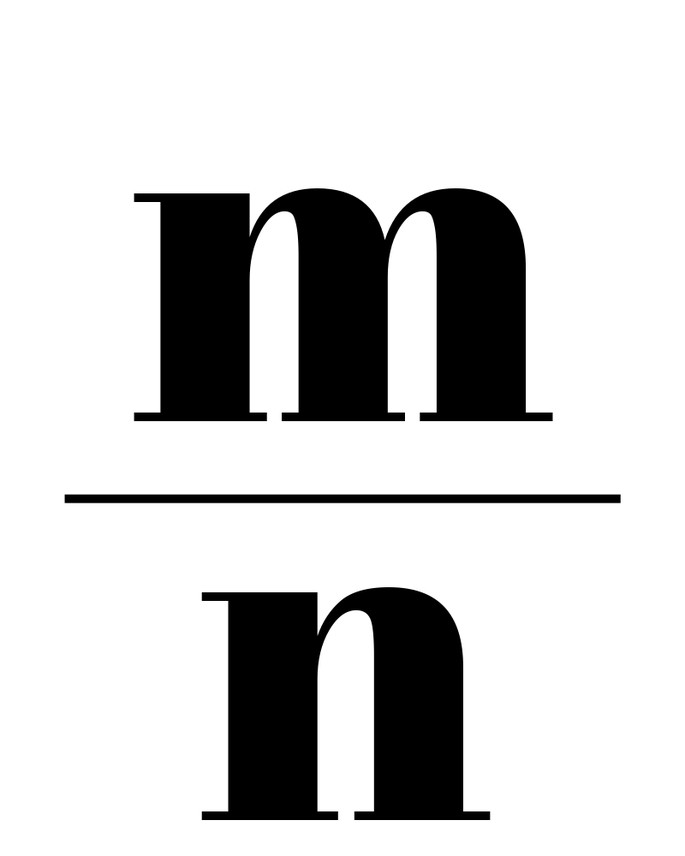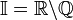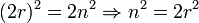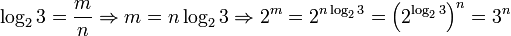Что такое мера иррациональности

ИРРАЦИОНАЛЬНОСТИ МЕРА

где минимум берется по всевозможным парам h₀, h₁ целых рациональных чисел таких, что

Понятие И. м. является частным случаем понятий линейной независимости меры и трансцендентности меры. И. м. показывает, насколько «хорошо» может число x быть приближено рациональными дробями. Для всех действительных иррациональных чисел x выполняется неравенство

но при любом e>0 для почти всех (в смысле меры Лебега) действительных x

где С=С(e, x)>0. Однако для любой функции j(H)->0 при и j(H)>0 существует число такое, что при всех

Лит.:[1] Xинчин А. Я., Цепные дроби, 3 изд., М. 1978.

Смотреть что такое «ИРРАЦИОНАЛЬНОСТИ МЕРА» в других словарях:

Открытые математические проблемы — Открытые (нерешённые) математические проблемы проблемы, которые рассматривались математиками, но до сих пор не решены. Часто имеют форму гипотез, которые предположительно верны, но нуждаются в доказательстве. В научном мире популярна… … Википедия

Пи (число) — У этого термина существуют и другие значения, см. Пи (значения). Иррациональные числа γ ζ(3) √2 √3 √5 φ α e π δ Система счисления Оценка числа … Википедия

e (число) — У этого термина существуют и другие значения, см. E. Не следует путать с Числами Эйлера I рода. Не следует путать с постоянной Эйлера. Иррациональные числа γ ζ(3) √2 √3 √5 φ α e π δ … Википедия

Трансцендентное число — (от лат. transcendere переходить, превосходить) это вещественное или комплексное число, не являющееся алгебраическим иными словами, число, которое не может быть корнем многочлена с целыми коэффициентами. Содержание 1 Свойства 2… … Википедия

ДИАЛЕКТИКА — (от греч. dialektike (techne) искусство вести беседу, спор) филос. теория, утверждающая внутреннюю противоречивость всего существующего и мыслимого и считающая эту противоречивость основным или даже единственным источником всякого движения и… … Философская энциклопедия

Непрерывная дробь — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия

Функция Минковского — Функция Минковского. Функция «вопросительный знак» Минковского построенная Германом Минковским монотонная с … Википедия

Подходящая дробь — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (то есть положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия

Подходящие дроби — Цепная дробь (или непрерывная дробь) это математическое выражение вида где a0 есть целое число и все остальные an натуральные числа (то есть положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или… … Википедия

Источник

Иррациональные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение иррациональных чисел

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:

Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

Примеры иррациональных чисел:

Множество иррациональных чисел договорились обозначать латинской буквой I.

Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Свойства иррациональных чисел

Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.

Свойства иррациональных чисел:

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Определение рациональных чисел

А теперь наоборот: рассмотрим противоположное заданной теме определение.

Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.

Рациональные числа — это те, которые можно представить в виде:

где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Основные свойства действий с рациональными числами

Источник

Число Лиувилля

Числа Лиувилля «почти рациональны» и поэтому могут быть «довольно точно» аппроксимированы последовательностями рациональных чисел. Это в точности те трансцендентные числа, которые можно более точно аппроксимировать рациональными числами, чем любое алгебраическое иррациональное число. В 1844 году Джозеф Лиувилль показал, что все числа Лиувилля трансцендентны, тем самым впервые установив существование трансцендентных чисел. [ необходима цитата ]

π и e не являются числами Лиувилля. [1]

Здесь мы показываем, что числа Лиувилля существуют, демонстрируя конструкцию, которая производит такие числа.

Из определения x следует, что его базовым b- представлением является

Теперь для любого целого n ≥ 1 определим q _n и p _n следующим образом:

Следовательно, мы заключаем, что любой такой x является числом Лиувилля.

Примечания к доказательству

Из этого следует заявленный вывод.

Теперь для любого целого n > 1 + log ₂ ( d ) последнее неравенство выше влечет

Следовательно, число Лиувилля, если оно существует, не может быть рациональным.

Рассмотрим, например, число

Более того, числа Лиувилля образуют плотное подмножество множества действительных чисел.

Для натуральных чисел n > 2 и q ≥ 2 установите:

Заметим, что для каждого натурального числа n ≥ 2 и m ≥ 1 мы также имеем

Напротив, мера Лебега множества всех реальных трансцендентных чисел бесконечна (так как набор алгебраических чисел является нулевым множеством ).

Для каждого положительного целого числа n установите

Таким образом, множество всех чисел Лиувилля можно записать как

Практически все числа имеют показатель иррациональности, равный 2. [3] : 246

Ниже приводится таблица известных верхних и нижних оценок мер иррациональности некоторых чисел.

Примеры включают 1, 2 и 0,5

База иррациональности

Ниже мы покажем, что никакое число Лиувилля не может быть алгебраическим.

По теореме о среднем значении существует x ₀ между p / q и α такое, что

Поскольку α является корнем f, а p / q нет, мы видим, что | f ′ ( x ₀ ) | > 0, и мы можем переставить:

что противоречит лемме. Следовательно, если число Лиувилля существует, оно не может быть алгебраическим и, следовательно, должно быть трансцендентным.

Источник

Иррациональность

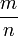
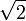
Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби , где m — целое число, n — натуральное число. О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа .

Множество иррациональных чисел обычно обозначается 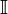. Таким образом

— множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

Содержание

Свойства

Теоремы

— иррациональное число

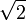
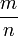
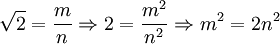
Допустим противное: рационален, то есть представляется в виде несократимой дроби , где m и n — целые числа. Возведём предполагаемое равенство в квадрат:

.

log₂3 — иррациональное число

Но 2 m чётно, а 3 n нечётно. Получаем противоречие.

e — иррациональное число

Другие иррациональные числа

Полезное

Смотреть что такое «Иррациональность» в других словарях:

иррациональность — непостижимость, трансцендентность, непознаваемость, нерациональность Словарь русских синонимов. иррациональность см. непознаваемость Словарь синонимов русского языка. Практический справочник. М.: Русский яз … Словарь синонимов

ИРРАЦИОНАЛЬНОСТЬ — ИРРАЦИОНАЛЬНОСТЬ, иррациональности, мн. нет, жен. (книжн.). отвлеч. сущ. к иррациональный. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

иррациональность — ИРРА ИОНАЛЬНЫЙ, ая, ое; лен, льна. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ИРРАЦИОНАЛЬНОСТЬ — недоступность рассудку. Иррациональное (лат. irrationalis – неразумное) – то, что не может быть постигнуто разумом, что явно не подчиняется законам логики, что оценивается как «сверхразумное», «противоразумное»; ср. Трансинтеллигибельный,… … Философская энциклопедия

иррациональность — иррациональное число иррациональное выражение иррациональный — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы иррациональное числоиррациональное… … Справочник технического переводчика

Иррациональность — I ж. отвлеч. сущ. по прил. иррациональный I II ж. отвлеч. сущ. по прил. иррациональный II Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

иррациональность — иррациональность, иррациональности, иррациональности, иррациональностей, иррациональности, иррациональностям, иррациональность, иррациональности, иррациональностью, иррациональностями, иррациональности, иррациональностях (Источник: «Полная… … Формы слов

Иррациональность — (см. Иррационализм) 1) недоступный рассудку; то, что не может быть постигнуто разумом, что явно не подчиняется законам логики, что оценивается как «сверхразумное», «противоразумное» (противоположный рациональный); 2) (в математике) несоизмеримый… … Начала современного естествознания

иррациональность — иррацион альность, и … Русский орфографический словарь

Иррациональность — математик. теория взаимно несоизмеримых величин. В значительной мере идентична совр. теории иррациональных чисел, однако в античности не было понятия иррационального числа … Словарь античности

Источник

Рациональные и иррациональные числа. Множество действительных чисел

Понятие рационального числа

Примеры рациональных чисел:

Любое рациональное число представимо в виде конечной или периодической бесконечной десятичной дроби.

Алгоритм перевода десятичной периодической дроби в обыкновенную дробь

Для смешанной периодической дроби – в знаменателе записать столько девяток, сколько цифр в периоде и справа дописать столько нулей, сколько цифр в дробной части до периода.

Шаг 3. Если необходимо, сократить полученную дробь

Чистые периодические дроби:

Смешанные периодические дроби:

Иррациональные числа

Примеры иррациональных чисел:

Множество иррациональных чисел не замкнуто относительно операции сложения.

Мера иррациональности действительного числа a – действительное число μ, которое показывает, насколько хорошо число a может быть приближено рациональными числами.

$μ(a) = 1 \iff a$ – рациональное число

Для многих трансцендентных чисел мера иррациональности неизвестна, есть только верхняя оценка.

Алгебраические и трансцендентные числа

Если действительное число является корнем уравнения вида

Алгебраические числа бывают рациональными и иррациональными.

Примеры трансцендентных чисел:$ π,2^<\sqrt2>, sin10^0, e^4$

Все трансцендентные числа иррациональны.

Т.е., трансцендентных чисел «больше», чем алгебраических. Их слишком много, чтобы можно было представить в виде последовательности.

Структура множества действительных чисел

Из-за несовпадения подмножеств, структуру множества действительных чисел можно представить двумя равносильными схемами:

Множество действительных чисел несчётно.

Множество действительных чисел замкнуто относительно операций сложения, вычитания, умножения и деления (исключая деление на 0).

В алгебре говорят, что действительные числа образуют непрерывное упорядоченное поле.

Примеры

Пример 1. Найдите рациональные дроби, равные данным бесконечным периодическим десятичным дробям:

Источник