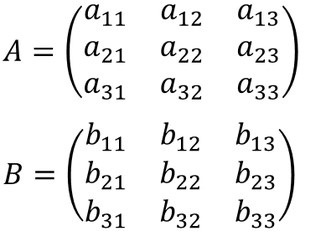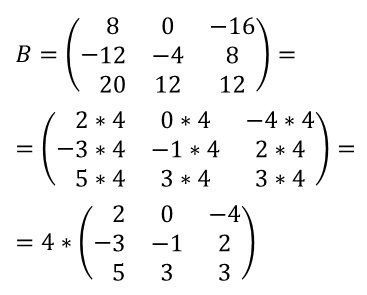Что такое матрица в математике простыми словами
Знакомство с матрицами
Понятие и базовые операции.
Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.
Что такое матрица
Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.
Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.
Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.
В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.
Общая схема матрицы 
Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три
Простые операции с матрицами
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.
И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.
Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре 
Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений
Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.
Пример умножения матрицы на число
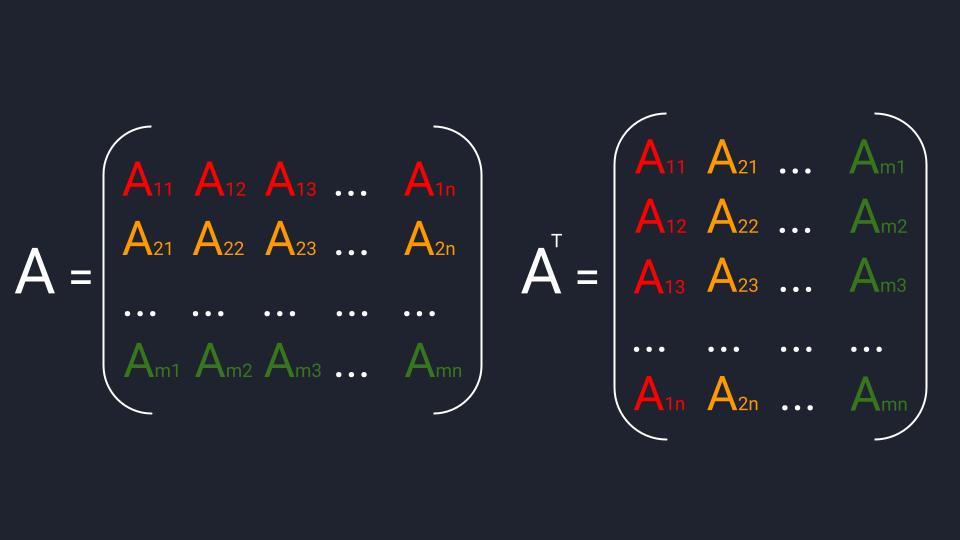
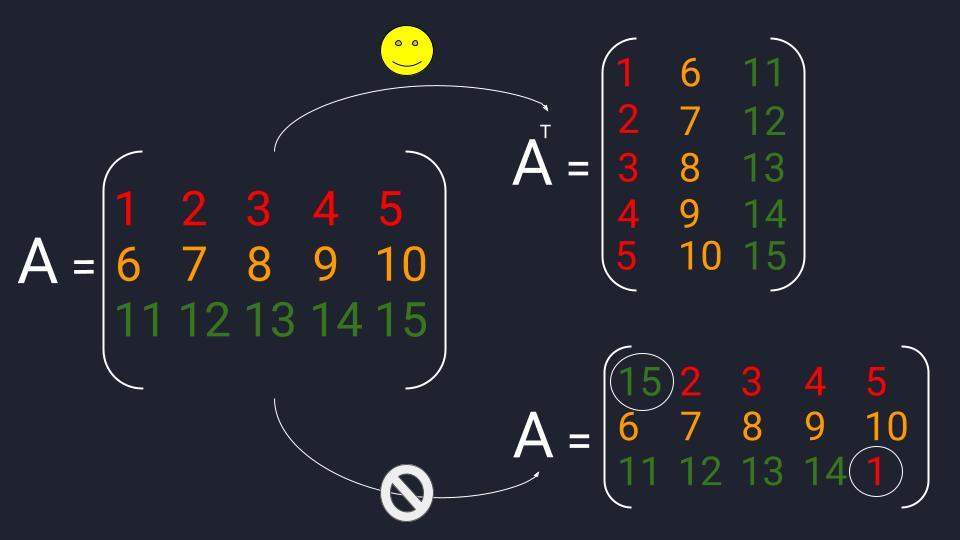
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.
⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.
Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы 
Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» 
Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил
Сложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.
Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами 
Пример вычитания двух матриц
Умножение матриц
Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.
Формула умножения матриц 
Пример умножения квадратных матриц размерностью 2×2
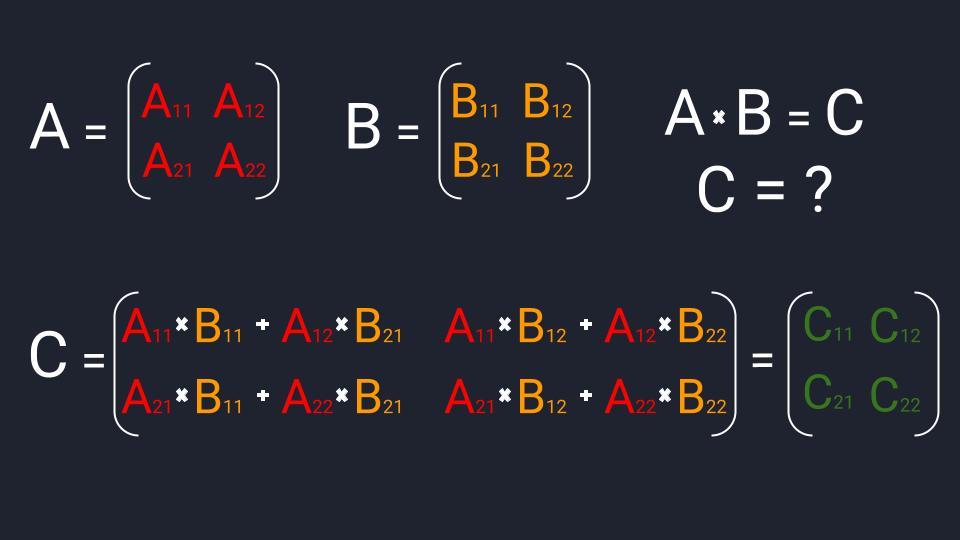
Что дальше
В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽
Что такое матрица в математике простыми словами
Обновлено: 08 Августа 2021
Матрица имеет множество значений в разных областях науки и техники. Конкретно в математике это объект, который облегчает вычисления и позволяет легко систематизировать любую информацию. Именно поэтому так необходимо знать, как ею пользоваться. Что же такое матрица?
Что такое матрицы в математике
Матрица — это таблица элементов, которая состоит из строк (m) и столбцов (n).
Может иметь разные размеры и формы в зависимости от количества находящихся в ней элементов. Элементы фиксированы: если переставить хотя бы один, то получится иная матрица с иными свойствами.
Откуда они взялись, чем полезны
Первые упоминания найдены еще в Древнем Китае, однако широкую известность матрицы приобрели только в середине XVIII, аккурат после выхода книги «Введение в анализ алгебраических кривых» Габриэля Крамера. В своей работе знаменитый математик описал совершенно новый способ решения систем линейных уравнений, который прозвали «методом волшебных квадратов». Сам термин «матрица» появился лишь в XIX веке благодаря трудам английского математика Д.Д. Сильвестра.
В современном мире матрицы используют повсюду. Телефонные справочники, табели успеваемости, отчеты и счета тоже являются матричными моделями. Они полезны, так как имеют прикладное значение.
Основные определения и обозначения матриц
В большинстве случаев матрицы обозначают прописными латинскими буквами (A, B, C), а ее элементы — строчными.
Виды матриц зависят от количества строк m и столбцов n. Основные из них:
Также существует понятие детерминант — это определитель свойств квадратной матрицы, который чаще всего используют в решении систем линейных алгебраических уравнений (СЛАУ).
Применение матриц в математико-экономическом моделировании
В математико-экономическом моделировании матрицы считаются самым удобным способом хранения различных структурированных данных и решения задач с ними. Приведем простой пример из экономической модели «затраты-выпуск».
Дана таблица распределения ресурсов по различным отраслям:
Так, элемент а23 = 5,8 обозначает то, сколько водных ресурсов потребляется в торговле, а элемент а11 = 4,8 обозначает, сколько трудовых ресурсов потребляется в промышленности.
Данная матрица может использоваться при сравнении и оценке востребованности ресурсов в различных отраслях экономики, решении экономических задач предприятий и организаций, анализе затраченных средств в ходе производства.
Решение матриц, основные операции с примерами и объяснением
Матрицы можно складывать и вычитать, умножать на определенное число, умножать между собой. Подробнее остановимся на основных операциях.
Сложение и вычитание матриц
Сложение и вычитание матриц возможно только в том случае, если они равны по размеру.
Чтобы сложить две матрицы, нужно сложить их соответствующие элементы.
С вычитанием действуем аналогичным образом.
Умножение матрицы на число
Чтобы умножить целую матрицу на число, необходимо умножить каждый элемент матрицы на это число.
Подметим, что дроби вносить в матрицу не нужно, поскольку это затрудняет дальнейшие операции.
Вынесение общего множителя за знак матрицы
Для вынесения общего множителя за знак матрицы необходимо найти общий множитель для всех элементов.
Подметим, что вынести общий множитель из строки или столбца невозможно.
Вынесение знака (минуса) за матрицу
При выполнении различных действий с матрицами большое количество минусов может привести к ошибкам и просчетам, поэтому обычно их выносят за матричную модель. Делается это при помощи замены всех знаков элементов. К примеру:
Таким образом, вероятность путаницы уменьшается за счет увеличения положительных коэффициентов.
Изучение матричных моделей не самое простое занятие. Если у вас нет времени на учебу, Феникс.Хелп может помочь в написании контрольных работ, статей и диссертаций. Переходите по ссылке и получаете квалифицированную помощь прямо сейчас!
Виды матриц и для чего они нужны простыми словами
Обновлено: 12 Августа 2021
При решении алгебраических или дифференциальных уравнений студенты сталкиваются с понятием матрицы. Этот термин используется в программировании, электронике, фотоискусстве, но основная область применения — математика. Рассмотрим, что это такое, как применяется и какие операции позволяет осуществить.
Что такое матрицы в математике
Матрица в математике — это абстрактный объект, имеющий вид таблицы чисел или других математических величин. Чаще таблица прямоугольная, но встречаются и другие виды (квадратные, треугольные).
Обычно матрица называется заглавной буквой латинского алфавита: матрица A, матрица B. В таблице есть строки (их количество называется m) и столбцы (их количество называется n). Количество строк и столбцов определяет размер матрицы и может называться порядком. Матрицы такого типа называются матрицами строения m×n, или размера m×n, или порядка m×n.
Элементы матрицы, т.е. числа или остальные величины, называются строчной буквой. Они имеют 2 нижних индекса, необходимых для определения их положения в матрице. Например, элемент a13 располагается на пересечении 2 строки и 3 столбца. Значения элемента а13 читаются по-отдельности, не как целое число: «а один-три».
Откуда они взялись и чем полезны
Первые упоминания матрицы появились в Древнем Китае. Это была квадратная таблица, получившая название магического или волшебного квадрата. Самым древним и известным считается квадрат 3×3, датируемый около 2200 г до н.э. Он был высечен на панцире черепахи. В Китае его называют квадрат Ло Шу, а в Западной Европе — «Печать Сатурна».
Таким же древним является квадрат, найденный в Кхаджурахо, столице средневекового государства Чандела (IX–XIII вв.) в Центральной Индии. Это первый из «дьявольских квадратов». Также он называется пандиагональным.
В древности матрицы были необходимы преимущественно для решения линейных уравнений. Когда матрицы появились в арабских странах, стали разрабатываться принципы работы с ними, в том числе, принцип сложения. В XVIII веке швейцарский математик, «отец линейной алгебры» Габриэль Крамер опубликовал правило Крамера. Это способ решения систем линейных уравнений с помощью матрицы.
Способ Крамера не подходит для решения тех систем линейных уравнений, в которых может быть бесконечное множество решений.
В следующем веке появляется метод немецкого математика Карла Фридриха Гаусса. Этот способ решения алгебраических уравнений не является открытием ученого. Впервые о методе Гаусса написали в китайском трактате «Математика в девяти книгах», а сам он только привел способ в удобную форму.
Для решения уравнений таким способом необходимо записать расширенную матрицу системы.
В отличие от метода Крамера, правило Гаусса можно использовать для решения любых систем линейных уравнений.
Детальная разработка теории матриц активно продолжилась с середины XIX века. Наиболее значимые ученые: Уильям Гамильтон, Артур Кэли, Карл Вейерштрасс, Мари Энмон Камиль Жордан, Фердинанд Георг Фробениус.
Сам термин «матрица» предложил английский математик Джеймс Сильвестр в 1850 г.
В наше время матрицы используются не только для записи и решения систем линейных уравнений. Списки, статистические данные, табеля с информацией — все это в какой-то степени матрица. Их применяют для упрощения подачи и работы с информацией в любой сфере. Например, таблица продаж, где указан год (первый столбец), вид продукции (первая строка), а остальные значения — количество проданных единиц.
Обозначения матриц
Помимо самого термина «матрицы», при их решении нужно знать и другие обозначения.
Элементы матрицы — любые математические объекты: числа, переменные, другие матрицы. Элемент обозначается как aab, где a — номер строки расположения элемента, b — номер столбца.
Главная диагональ матрицы — диагональ, пересекающая квадратную матрицу из верхнего левого угла в нижний правый угол (квадратные матрицы имеют одинаковое количество строк и столбцов). Прямоугольные матрицы также могут иметь диагонали: они пересекают элементы с одинаковыми индексами.
Побочная диагональ матрицы — диагональ, пересекающая верхний правый и нижний левый углы. Для прямоугольного вида матриц понятие «побочные диагонали» не используется.
Диагональные элементы — числа и другие математические величины матрицы, расположенные на главной диагонали.
Размер (порядок) матрицы — произведение количества строк на количество столбцов: m×n. Например, если матрица содержит 2 строки и 3 столбца, то ее обозначают матрицей 2×3.
След матрицы — сумма элементов матрицы, расположенных на главной диагонали. Обозначается как Sp (А) или Tr (A), где A — название матрицы.
Равные матрицы — матрицы, у которых соответствующие элементы равны.
Виды матриц, какие бывают
В математике существует несколько видов матриц в зависимости от их размера.
Также различают матрицы по значениям их элементов.
Треугольная матрица всегда квадратная: m=n.
Кососимметрическая матрица всегда квадратная.
Применение матриц в математико-экономическом моделировании
С древности и по настоящее время матрицы используются для решения и удобной записи системы линейных алгебраических или дифференциальных уравнений. Но их также применяют в математико-экономическом моделировании для структурирования данных и комфортной работы с ними.
Наиболее популярной является матричная модель экономики «затраты–выпуск». Ее внедрил Василий Леонтьев — американский экономист. За развитие этого метода он получил нобелевскую премию: матричная модель упростила решение некоторых экономических проблем. В последствии Леонтьева стали называть «апостолом планирования».
Суть модели «затраты–выпуск» в том, что экономист разделил производственный сектор экономики на отрасли, число которых обозначается n. 1 отрасль — 1 вид продукции. Значит, n количество отраслей выпускает n количество продуктов. Это приводит к появлению межотраслевых связей: одна отрасль заимствует у другой продукт и использует в процессе производства своей продукции. Данная балансовая модель представлена в виде системы линейных уравнений, решаемых с помощью матрицы.
Какие операции можно производить с матрицами
С матрицами можно проводить несколько операций.
При умножении матрицы нельзя менять местами.
Примеры решения задач на матрицы
Пример решения задачи на умножение.
Найдем значение каждого элемента:
Пример решения задачи на умножение матрицы на число 5.
Учитесь работать с матрицами и продолжайте осваивать математику, а если задач накопилось слишком много и «горят» сроки, вам поможет сервис Феникс.Хелп. Обращайтесь!
Математика для чайников. Матрицы и основные действия над ними
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
От действий над матрицами к пониманию их сути…
Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.
Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.
Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.
Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.
Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.
Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…
Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.
Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?
Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…
Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.
В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.
Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».