Что такое матрица смежности графа
Матрица смежности
Матрица смежности — один из способов представления графа в виде матрицы.
Содержание
Определение
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.
Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i-й вершины.
Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.
Примеры
Свойства
Матрица смежности неориентированного графа симметрична, а значит обладает действительными собственными значениями и ортогональным базисом из собственных векторов. Набор её собственных значений называется спектром графа, и является основным предметом изучения спектральной теории графов.
Два графа G1 и G2 с матрицами смежности A1 и A2 являются изоморфными если и только если существует перестановочная матрица P, такая что
Из этого следует, что матрицы A1 и A2 подобны, а значит имеют равные наборы собственных значений, определители и характеристические многочлены. Однако обратное утверждение не всегда верно — два графа с подобными матрицами смежности могут быть неизоморфны.
Степени матрицы
Если A — матрица смежности графа G, то матрица править] Структура данных
Матрица смежности и cписки смежности являются основными структурами данных, которые используются для представления графов в компьютерных программах
Использование матрицы смежности предпочтительно только в случае неразреженных графов, с большим числом рёбер, так как она требует хранения по одному биту данных для каждого элемента. Если граф разрежён, то большая часть памяти напрасно будет тратиться на хранение нулей, зато в случае неразреженных графов матрица смежности достаточно компактно представляет граф в памяти, используя примерно 
В алгоритмах, работающих со взвешенными графами (например в алгоритме Флойда-Уоршелла), элементы матрицы смежности вместо чисел 0 и 1, указывающих на присутствие или отсутствие ребра, часто содержат веса самих ребер. При этом на место отсутствующих ребер ставят некоторое специальное граничное значение (англ. sentinel ), зависящее от решаемой задачи, обычно 0 или 
Что такое матрица смежности графа
Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.
Классификация графов
В связном графе между любой парой вершин существует как минимум один путь.
В несвязном графе существует хотя бы одна вершина, не связанная с другими.
Графы также подразделяются на
В ориентированном графе ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.
В неориентированном графе по каждому из ребер можно осуществлять переход в обоих направлениях.
Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер.
Способы представления графа
Граф может быть представлен (сохранен) несколькими способами:
Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Размер массива зависит от количества вершин и/или ребер в конкретном графе.
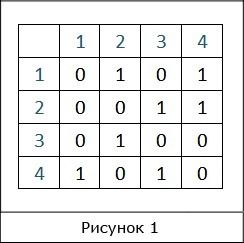
Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.
Число строк матрицы смежности равно числу столбцов и соответствует количеству вершин графа.

Когда из одной вершины в другую проход свободен (имеется ребро), в ячейку заносится 1, иначе – 0. Все элементы на главной диагонали равны 0 если граф не имеет петель.
Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).
В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.
Матрица инцидентности для своего представления требует нумерации рёбер, что не всегда удобно.
Список смежности (инцидентности)
Если количество ребер графа по сравнению с количеством вершин невелико, то значения большинства элементов матрицы смежности будут равны 0. При этом использование данного метода нецелесообразно. Для подобных графов имеются более оптимальные способы их представления.
По отношению к памяти списки смежности менее требовательны, чем матрицы смежности. Такой список можно представить в виде таблицы, столбцов в которой – 2, а строк — не больше, чем вершин в графе.
В каждой строке в первом столбце указана вершина выхода, а во втором столбце – список вершин, в которые входят ребра из текущей вершины.
Преимущества списка смежности:
Недостатки списка смежности:
Алгоритмы обхода графов
Основными алгоритмами обхода графов являются
Поиск в ширину подразумевает поуровневое исследование графа:
Вершины просматриваются в порядке возрастания их расстояния от корня.
Алгоритм прекращает свою работу после обхода всех вершин графа, либо в случае выполнения требуемого условия (например, найти кратчайший путь из вершины 1 в вершину 6).
Каждая вершина может находиться в одном из 3 состояний:
Фиолетовый – рассматриваемая вершина. 
Применения алгоритма поиска в ширину
Алгоритм поиска в ширину работает как на ориентированных, так и на неориентированных графах.
Для реализации алгоритма удобно использовать очередь.
Реализация на C++ (с использованием очереди STL)
Результат выполнения
Задача поиска кратчайшего пути
Реализация на С++
Поиск в глубину – это алгоритм обхода вершин графа.
Поиск в ширину производится симметрично (вершины графа просматривались по уровням). Поиск в глубину предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность продвижения означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина).
Отсутствие последнего свидетельствует об одной из двух возможных ситуаций:
Каждая вершина может находиться в одном из 3 состояний:
Фиолетовый – рассматриваемая вершина. 
Применения алгоритма поиска в глубину
Алгоритм поиска в глубину работает как на ориентированных, так и на неориентированных графах. Применимость алгоритма зависит от конкретной задачи.
Для реализации алгоритма удобно использовать стек или рекурсию.
Реализация на C++ (с использованием стека STL)
Результат выполнения 
Задача поиска лексикографически первого пути на графе.
Реализация на C++
Результат выполнения 
Поиск в глубину также может быть реализован с использованием рекурсивного алгоритма.
Реализация обхода графа в глубину на C++ (с использованием рекурсии)
Матрица смежности
Представление матрицы смежности
Пример матрицы смежности
Изображение ниже показывает график и его эквивалентную матрицу смежности.
В случае неориентированного графа матрица симметрична относительно диагонали, потому что у каждого ребра (i, j) также есть ребро (j, i).
Плюсы матрицы смежности
Основные операции, такие как добавление ребра, удаление ребра и проверка наличия ребра от вершины i до вершины j, являются чрезвычайно эффективными по времени операциями. Операциями с постоянным временем.
Если граф плотный и число ребер велико, матрица смежности должна стать первым выбором. Даже если граф и матрица смежности разрежены, мы можем представить ее, используя структуры данных для разреженной матрицы.
Однако самое большое преимущество исходит от использования матриц. Последние достижения в области аппаратного обеспечения позволяют нам выполнять даже дорогостоящие матричные операции на графическом процессоре (GPU).
Выполняя операции над смежной матрицей, мы можем получить важную информацию о природе графа и взаимосвязи между его вершинами.
Минусы матрицы смежности
Из-за требования к пространству матрицы смежности VxV может быть недостаточно памяти. Но обычно графы не имеют слишком много соединений, и это главная причина, почему списки смежности являются лучшим выбором для большинства задач.
Хотя базовые операции просты, такие операции, как inEdges и outEdges, дороги при использовании представления матрицы смежности.
Код матрицы смежности
Если вы знаете, как создавать двумерные массивы, значит вы также знаете, как создать матрицу смежности.
Матрица смежности в C++
Матрица смежности в Java
Матрица смежности в Python
Рекомендуем хостинг TIMEWEB
Рекомендуемые статьи по этой тематике
Инцидентность и смежность в графах, матрицы смежности, матрицы инцидентности, списки инцидентности
Инцидентность вершин и рёбер графа, смежность вершин графа
Пример 1. Задать аналитически граф, представленный на рисунке ниже. (рис. А)
Итак, задаём граф следующими множествами:
Зададимся вопросом: можно ли поместить слона в компьютер? Ответ: можно, если слона смоделировать в виде графа, в котором вершинами являются части его тела, а рёбра соединяют те части тела, которые соединены в слоне как биологическом объекте. При этом получившийся граф должен быть представлен в памяти компьютера в понятном компьютеру виде.
В связи с широким применением графов в программировании и информационных технологиях вообще возникает вопрос о представлении графа в виде структуры данных. Различные способы представления графов в памяти компьютера отличаются объёмом занимаемой памяти и скоростью выполнения операций над графами.
Матрицы смежности
Матрица смежности для неориентированного графа
Элемент матрицы смежности s ij неориентированного графа определяется следующим образом:
— равен единице, если вершины v i и v j смежны;
— равен нулю, если вершины v i и v j не смежны.
Пример 2. Составить матрицу смежности для графа, представленного на рисунке ниже.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 |
| 3 | 1 | 0 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 |
Таким образом, матрица смежности неориентированного графа симметрична относительно главной диагонали.
Матрица смежности для ориентированного графа
Элемент матрицы смежности s ij ориентированного графа определяется следующим образом:
— равен единице, если из вершины v i в вершину v j входит дуга;
— равен нулю, если из вершины v i в вершину v j дуга не входит.
Пример 3. Составить матрицу смежности для графа, представленного на рисунке ниже.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 |
Таким образом, матрица смежности ориентированного графа не симметрична.
Матрица смежности для графа с кратными рёбрами
Пример 4. Составить матрицу смежности для графа, представленного на рисунке ниже.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 2 | 0 | 0 |
| 2 | 3 | 0 | 0 | 1 | 1 |
| 3 | 2 | 0 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 |
Матрица смежности для взвешенного графа
В случае взвешенного графа элемент матрицы смежности s ij равен числу w, если существует ребро между вершинами v i и v j с весом w. Элемент s ij равен нулю, если рёбер между вершинами v i и v j не существует.
Пример 5. Составить матрицу смежности для графа, представленного на рисунке ниже.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 11 | 9 | 0 | 0 |
| 2 | 11 | 0 | 0 | 5 | 8 |
| 3 | 9 | 0 | 0 | 0 | 2 |
| 4 | 0 | 5 | 0 | 0 | 0 |
| 5 | 0 | 8 | 2 | 0 | 0 |
Матрицы инцидентности
Матрица инцидентности для неориентированного графа
Элемент матрицы инцидентности для неориентированного графа h ij определяется следующим образом:
— равен единице, если вершина v i инцидентна ребру e j ;
Пример 6. Составить матрицу инцидентности для графа, представленного на рисунке ниже.
| V | 1-2 | 1-3 | 2-4 | 2-5 | 3-5 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 1 |
Матрица инцидентности для ориентированного графа
Элемент матрицы инцидентности для ориентированного графа h ij определяется следующим образом:
— равен минус единице, если вершина v i является началом ребра e j ;
— равен единице, если вершина v i является концом ребра e j ;
Пример 7. Составить матрицу инцидентности для графа, представленного на рисунке ниже.
| V | 1-2 | 1-3 | 2-4 | 2-5 | 3-5 |
| 1 | 1 | -1 | 0 | 0 | 0 |
| 2 | -1 | 0 | -1 | -1 | 0 |
| 3 | 0 | 1 | 0 | 0 | -1 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 1 |
Списки инцидентности
Графы значительного объёма целесообразно хранить в памяти компьютера в форме списков инцидентности.
Список инцидентности одной вершины графа включает номера вершин, смежных с ней.
Ссылки на начало этих списков образуют одномерный массив, индексами которого служат номера вершин графа.
Пример 8. Составить списки инцидентности для графа, представленного на рисунке ниже.
Преимущества и недостатки каждого способа
Матрицы смежности и инцидентности целесообразнее использовать когда:
Из-за последнего обстоятельства матрицы чаще используются в теоретических исследованиях графов.
Списки инцидентности целесообразнее использовать когда:
На практике списки чаще используются в прикладных целях.
В чем особенности представления графа матрицей смежности
Матрица смежности для графов
Матрица смежности графа является квадратной матрицей с элементами, каждый из которых имеет одно из двух значений: 0 или 1.
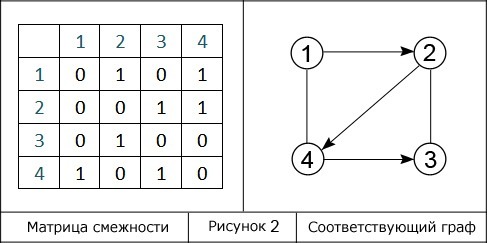
Простой пример матрицы смежности изображен на рисунке.
Данная матрица является двоичной квадратной, то есть количество строк в единичном случае соответствует количеству столбцов, а также строки и столбы имеют значения либо 1, либо 0. Первая строка и первый столбец, не состоящие в матрице, а записанные для легкости восприятия, содержат номера, на пересечении которых расположен каждый из элементов, и они определяют индексное значение последних. Достаточно просто выполнить построение матрицы данного типа, зная соответствующий ей граф.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В левой стороне на рисунке представлена аналогичная матрица смежности с размерностью 4х4. Числа, выделенные синим цветом, допустимо рассматривать в виде вершин смешанного графа, записанного в правой стороне – того, представлением которого является матрица.
Отобразить граф можно путем вычисления по матрице смежности числа его вершин и применения специального правила. В том случае, когда из одной вершины в другую проход свободен, то есть имеется ребро, в ячейку записывают 1, в противном случае – 0. Таким образом:
Заметим, что для элементов, расположенных на главной диагонали, характерно нулевое значение. Это является следствием отсутствия у графа петель. Однако, в информатике нет ограничений для записи некоторых или всех элементов на главной диагонали в виде единиц.
В чем особенности представления
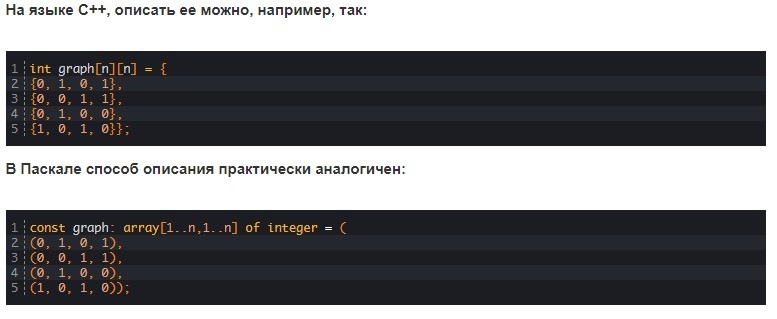
В программе матрицу смежности задают с помощью обычного двумерного массива. Его размерность соответствует n x n, где n является числом вершин графа.
В том случае, когда граф неизвестен заранее, а определен пользователем, необходимо вводить двумерный массив вручную. Это объясняется условиями работы конкретного языка программирования. При необходимости предоставления графа в виде матрицы смежности требуется \(O(|V|^<2>)\) памяти, так как ее размер соответствует квадрату числа всех вершин.
Если количество ребер графа в сравнении с числом вершин является небольшим, значения многих элементов матрицы смежности будут соответствовать нулю. Таким образом, применение рассматриваемой методики нецелесообразно, в связи с наличием для подобных графов наиболее эффективных способов представления.
Списки смежности и списки ребер, плюсы и минусы
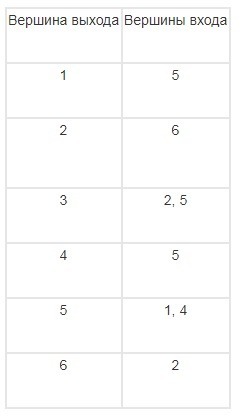
В данном случае, граф состоит из 6 вершин (|V|) и 5 ребер (|E|). Из последних 2 ребра являются направленными и 3 ненаправленными. При этом из каждой вершины выходит, как минимум одно ребро в другую вершину. Таким образом, список смежности рассматриваемого графа содержит |V| строк.
В i строке и 1 столбце указана вершина выхода, а в i строке и 2 столбце – вершина входа. Например, из вершины 5 выходят два ребра, входящие в вершины 1 и 4.
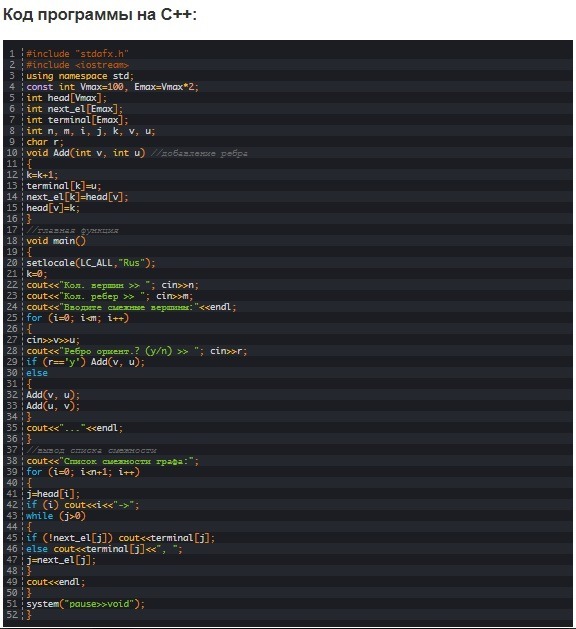
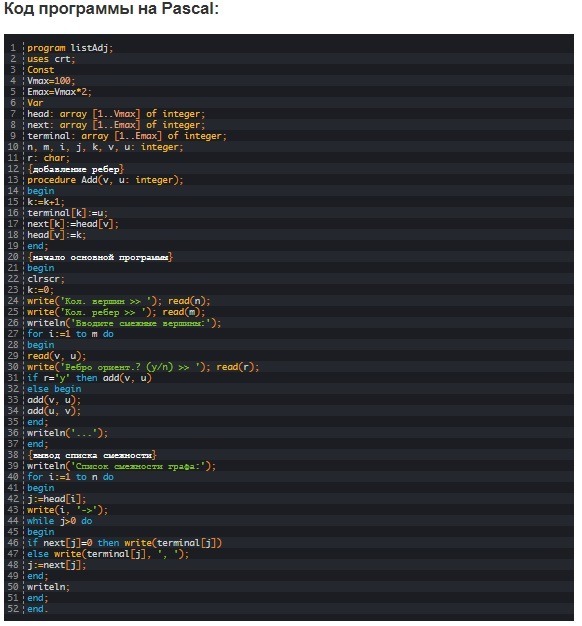
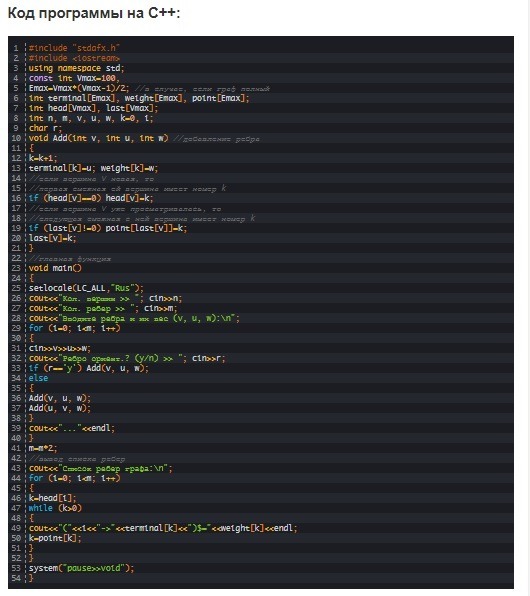
В процессе программной реализации списка смежности число вершин и ребер задают с помощью клавиатуры. Можно установить лимиты, то есть задать пару констант, одна из которых определяет максимально допустимое число вершин (Vmax), другая – ребер (Emax). Затем следует использовать три одномерных целочисленных массива:
Допустимым действием является выделение в программе двух ключевых частей. К ним относят ввод ребер для дальнейшего добавления их в список смежности и вывод полученного списка смежности на экран.
В первую очередь выполняют запрос на ввод суммы вершин (n) и ребер (m) графа (данная информация должна быть у пользователя). Следующим шагом является запуск цикла ввода ребер, то есть смежных вершин. Условие в этом цикле нужно для того, чтобы узнать, какое введено ребро.
Если введено направленное ребро, то функция add вызывается 1 раз, иначе – 2, тем самым внося сведения, что есть ребро как из вершины v в вершину u, так и из u в v. По окончанию формирования списка смежности происходит его отображение программой на экране.
Вывод на экран осуществляется:
Функция add производит добавление ребер в изначально пустой список смежности:
Действия реализуются, согласно алгоритму с формальными параметрами, вспомогательной переменной k и тремя одномерными целочисленными массивами:
В ячейке, где пересекаются i-ая строка и 2-ой столбец, могут быть записи нескольких элементов в соответствии с несколькими смежными вершинами. Можно обозначить каждую строку из списка смежности его подсписком. В результате выведенный список смежности будет включать элементы подсписков, отсортированные в обратном порядке. Обычно порядок вывода смежных вершин (в подсписках) не имеет принципиального значения.
Список со строками, содержащими запись двух смежных вершин и вес ребра, которое их соединяет, называют списком ребер графа. В качестве примера можно рассмотреть связный граф G=(V, E). Множество ребер E следует сгруппировать следующим образом:
Допустим, какая-либо величина p равна количеству всех ребер, которые включены в подмножество d, а s – то же самое относительно k. Тогда для графа G высотой списка ребер будет являться величина:
Таким образом, число строк из списка ребер в любом случае должно соответствовать величине, определенной по итогам сложения ориентированных ребер с неориентированными, умноженными на 2. Рассматриваемый способ представления графа предполагает хранение в каждой строке пары смежных вершин, а неориентированное ребро, которое соединяет вершины v и u, идет как из v в u, так и из u в v.
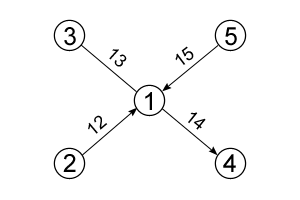
Например, имеется некий граф смешанного типа с 5 вершинами и 4 ребрами, каждому из которых соответствует определенное целое значение (для наглядности оно составлено из номеров вершин):
Граф содержит 3 направленных ребра и 1 ненаправленное. Путем подстановки значений в формулу можно определить высоту списка ребер: 3+1*2=5
На рисунке изображен список ребер для рассматриваемого графа. Таблица в размерах составляет n×3, где n= s+p*2=3+1*2=5. Элементы в первом столбце расположены по возрастанию, во втором – порядок расположения элементов определен первым, а в третьем – зависит от двух предыдущих.
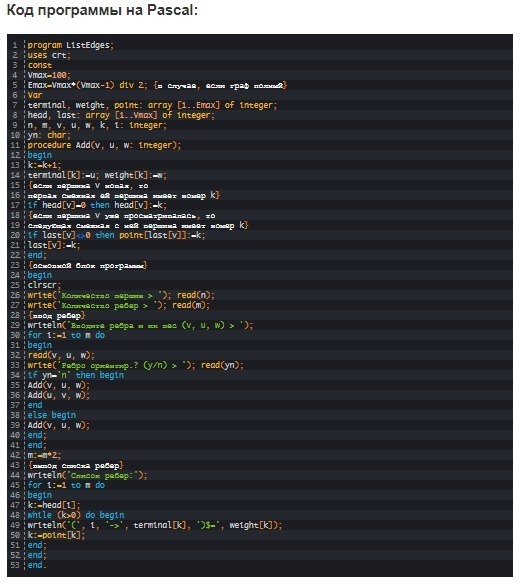
Список ребер реализуется программой. Процесс схож с операциями при реализации списка смежностей. В первую очередь организуют ввод данных, которые с помощью особой функции распределяются среди массивов. Затем происходит вывод полученного списка смежности на экран. В связи с необходимостью в использовании дополнительного массива, функция добавления ребер организована по-другому.
Максимально допустимое число вершин в графе определено с помощью константы Vmax, а количество ребер – Emax. Вторая константа инициализируется формулой Vmax*(Vmax-1)/2, вычисляющей количество ребер в полном графе при известном числе вершин.
Далее, в программах описываются 5 массивов:
По результатам ввода числа вершин (n) и ребер (m) графа будет запущен цикл, каждый этап которого сопровождается вводом пользователем с клавиатуры пары смежных вершин и веса ребра, расположенного между ними. Если ребро ориентированное, функция записи в список ребер (Add) вызывается единожды, при неориентированном ребре – дважды. Суммарное количество вызовов функции определяется по формуле:
где s – является ориентированными ребрами графа
p – неориентированные ребра
По итогам формирования списка ребер следует умножить на 2 переменную m. Это связано с тем, что при чисто неориентированном графе высота списка составляет:
Завершающим этапом является отображение на экране результирующей конструкции. В связи с тем, что на номер первой вершины, смежной с i-ой вершиной, указывает элемент head[i], каждая новая итерация внешнего цикла начинается с взятия этого номера (k=head[i]). Внутренний цикл прекращает реализацию в том случае, когда отсутствует смежная с i-ой вершины (k станет равной нулю), а внешний – по окончанию вывода списка ребер.
Ключевые действия, включая добавление ребра, удаление ребра, проверку наличия ребра от вершины i до вершины j, отличаются высокой эффективностью и являются операциями с постоянным временем. В том случае, когда граф плотный, а количество ребер большое, матрица смежности представляет собой наиболее целесообразное решение. Даже когда граф и матрица смежности разрежены, можно представить ее с помощью структур данных для разреженной матрицы.
Главное достоинство методики заключается в применении матриц. Благодаря передовым разработкам в сфере аппаратного обеспечения, представляется возможным реализовывать даже дорогостоящие матричные операции на графическом процессоре (GPU). В процессе выполнения операций со смежной матрицей можно получить ценные данные о природе графа и том, как связаны его вершины.
К минусам матрицы смежности можно отнести риски возникновения недостатка объема памяти по причине наличия требований к пространству матрицы смежности VxV. Однако, зачастую графы не обладают чрезмерно большим числом соединений, что является основным поводом выбрать списки смежности для решения распространенных задач.
С другой стороны, несмотря на простоту базовых операций, существуют такие операции, как inEdges и outEdges, которые отличаются дороговизной при использовании для представления матрицы смежности.
Классификация графов
Ярким примером графа является схема метро или некий другой маршрут. Программисты знакомы с компьютерной сетью, которая также представляет собой граф. Общим в этих примерах является наличие точек, соединенных линиями.
В случае компьютерной сети точками являются отдельные серверы, а линиями – разные типы электрических сигналов. В метрополитене точки можно принять за станции, а линии – за туннели, проложенные между станциями. Согласно теории графов, точки представляют собой вершины или узлы, а линии – ребра или дуги.
Граф является совокупностью вершин, которые соединены ребрами.
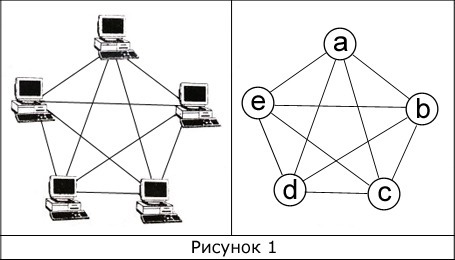
В математике преимущественно рассматривают не содержание, а структуру вещей, отделяя ее от всего остального. Данный прием позволяет определять какие-либо объекты, как графы. В случае компьютерной сети можно отметить наличие определенной топологии и возможности условного представления в виде некоторого количества компьютеров и соединительных путей. На рисунке изображена полносвязная топология:
Фактически такая топология является графом. Пять компьютеров представляют собой вершины, а соединения или пути передачи сигналов являются ребрами. Ели выполнить замену компьютеров на вершины, то в результате получится математический объект или граф с 10 ребрами и 5 вершинами. Нумерацию вершин допустимо выполнять произвольно.
В рассматриваемом примере не используются петли, то есть такие ребра, которые выходят из вершины и сразу же водят в нее. В теории графов существует ряд обозначений:
Применительно к рисунку:
В том случае, когда из любой вершины доступна другая вершина, граф является неориентированным и связным. При невыполнении данного условия для связного графа, его называет ориентированным или орграфом.
Степень вершины определяется числом ребер, которые соединяют ее с другими вершинами.
В сумме все степени графа соответствуют удвоенному количеству всех его ребер. К примеру, на рисунке изображен граф со суммой степеней, равной 20:
Орграф отличается от неориентированного графа возможностью перемещаться из вершины h в вершину s без промежуточных вершин лишь тогда, когда ребро выходит из h и входит в s, но не наоборот. Форма записи ориентированного графа:
где V – является вершинами, A – определяет направленные ребра.
К третьему типу относят смешанные графы. Такие графы включают направленные и ненаправленные ребра. Формальная запись смешанного графа:
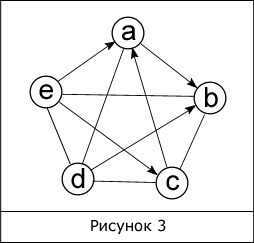
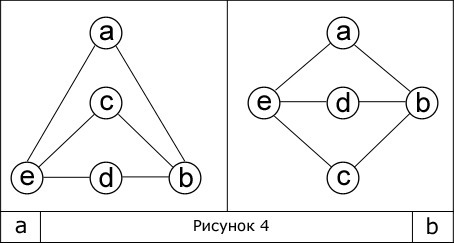
На рисунке изображен граф с направленными [(e, a), (e, c), (a, b), (c, a), (d, b)] и ненаправленными [(e, d), (e, b), (d, c)…] дугами. Предположим, что имеются два графа:
Данные графы эквиваленты друг другу, так как без изменений в структуре одного графа можно построить второй. Такие графы являются изоморфными, то есть обладают следующим свойством: какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На приведенном выше рисунке изображена пара изоморфных графов.
В случае, когда каждое ребро графа соответствует некоторому значению в виде веса ребра, граф является взвешенным. При решении задач можно встретить примеры, когда за вес принимают длину, цену маршрута и другие виды измерений. При графическом изображении графа принято указывать весовые значения около ребер.
Путь – последовательность вершин, каждая из которых связана с последующей с помощью ребра.
При совпадении первой и последней вершины путь называют циклом. Длина пути равна количеству составляющих его ребер. К примеру, на рисунке путь является последовательностью [(e), (a), (b), (c)]. Этот путь представляет собой подграф, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.
Способы представления графа, алгоритмы обхода
Граф, как и другие распространенные типы математических объектов, можно представить на компьютере, то есть сохранить в его памяти. Наиболее известные способы интерпретации графов:
Первые два метода заключаются в хранении графа в виде двумерного массива или матрицы. Размеры этих массивов определяются числом вершин и/или ребер в определенном графе. Таким образом, размер матрицы смежности – n×n (где n – число вершин), а матрицы инцидентности – n×m (n – число вершин, m – число ребер в графе).
В процессе решения многих задач с применением графов требуется обходить все вершины и ребра, то есть дуги. Обойти граф – значит, пройти все его вершины точно по одному разу. Алгоритмы обхода:
Реализация алгоритма обхода заключается в последовательном посещении вершин и исследовании ребер. Не посещенную вершину называют новой. После посещения вершину считают открытой до момента исследования всех инцидентных ей ребер. По итогу манипуляций вершина становится закрытой.
Обход в глубину выполняют, согласно следующим правилам:
Поиск в ширину отличается тем, что за активную принимается такая открытая вершина, которая была посещена последней. В том случае, когда выполняется обход в глубину, чем позднее будет посещена вершина, тем раньше она будет использована.
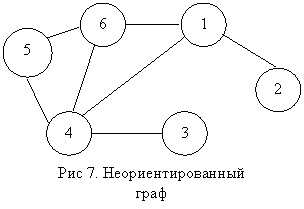
В качестве примера можно рассмотреть неориентированный граф, изображенный на рисунке:
Обход следует начинать со стартовой вершины 1. Она является активной и единственной, которая открыта. Другие вершины: 2,3,4,5,6 – новые. Вершина 1 обладает тремя инцидентными ребрами – 1–2, 1–4 и 1–6. Можно начать с ребра 1–2. В результате его прохождения открывается вершина 2. Она обладает одним инцидентным ребром 2–1, которое просмотрено. Вершина 2 была просмотрена, в результате чего она преобразуется в закрытую.
Затем по ребру 2–1 можно вернуться в вершину 1. По ребру 1– 4 легко попасть в вершину 4, которая становится открытой. Вершина 4 обладает четырьмя инцидентными ребрами: 4–1, 4–3, 4–5, 4–6. Таким образом, ребро 4–1 просмотрено.
Далее следует рассмотреть ребро 4–3. С его помощью удобно попасть в вершину 3, которая в результате становится открытой. Вершина 3 обладает одним инцидентным ребром 3–4. Данная вершина просмотрена. В результате вершина 3 закрыта, а по ребру 3–4 можно вернуться в вершину 4. Затем следует рассмотреть ребро 4 – 5.
Вершина 5 обладает двумя инцидентными ей ребрами: просмотренным (4–5) и ребром 5–6, по которому можно попасть в вершину 6. Вершина 6 обладает тремя инцидентными ей ребрами: просмотренным 6–5, 6–1 и 6–4. С помощью ребра 6–1 можно попасть в просмотренную вершину 1. По ребру 6–4 просто попасть в просмотренную вершину 4. В результате все вершины графа просмотрены. Порядок посещения вершин: 1, 2, 4, 3, 5, 6.
Основной особенностью и отличием поиска в ширину является выбор в виде активной вершины – такой, которая посещалась раньше, чем остальные. Таким образом, можно сформулировать ключевое свойство обхода в ширину: чем ближе вершина к старту, тем раньше она будет посещена.
Вершина используется путем просмотра одновременно всех вершин, которые ранее не были просмотрены и являются смежными с рассматриваемой вершиной. В результате поиск реализуют по всем вероятным направлением сразу. В первую очередь посещается вершина А, далее смежные с ней вершины, удаленные от А на 1.
Затем посещаются вершины, которые расположены на расстоянии 2 от А, и так далее. Чем ближе вершина к стартовой вершине, тем раньше она будет посещена. Поиск в ширину направлен на определение наиболее короткого из возможных путей.
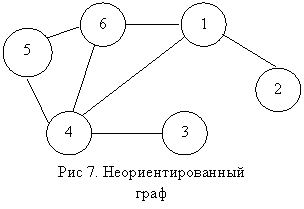
В качестве примера можно рассмотреть неориентированный граф, изображенный на рисунке:
Обход следует начать со стартовой вершины 1, которая является просмотренной. Вершины 2, 4, 6 и стартовая вершина – смежные. Данные вершины можно отметить, как просмотренные, и поместить в очередь. При рассмотрении вершины 2 можно заметить, что она не обладает смежными вершинами.
Затем нужно рассмотреть вершину 4 с двумя смежными вершинами 3 и 5. Их можно поместить в очередь и отметить, как просмотренные. В результате просмотрены все вершины графа. Порядок посещения вершин: 1, 2, 4, 6, 3, 5.
Как построить граф по матрице смежности
Данная методика отличается удобством, что позволяет представлять плотные графы с количеством ребер (|E|), которое приблизительно соответствует числу вершин в квадрате (|V|2). В процессе требуется заполнить матрицу размером |V| x |V| следующим образом:
A[i][j] = 1 (Если существует ребро из i в j)
Метод допустим к применению в случае ориентированных и неориентированных графов. Во втором варианте матрица A имеет вид симметричной, то есть A[i][j] == A[j][i]. Это объясняется тем, что при существовании ребра между i и j, оно является и ребром из i в j, и ребром из j в i. С помощью данного свойства сокращают практически вдвое объем требуемой памяти, в связи с тем, что элементы хранятся лишь в верхней части матрицы, над главной диагональю.