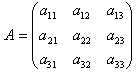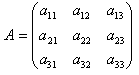Что такое матрица паскаль
Двумерные массивы
Одномерный массив можно представить как линейную структуру, в которой элементы следуют друг за другом. Однако бывают более сложные структуры данных. Например, двумерные массивы, которые можно описать как таблицу, в ячейках которой располагаются значения. Для обращения к данным массива указывается номера их строк и столбцов. Часто табличные массивы называют матрицами.
Обычно двумерные массивы на языке программирования Pascal описываются так:
Однако можно их описывать и по-другому:
При этом описание может быть в разделе type и тогда создается новый тип, который можно использовать при объявлении переменных. Или массив может быть описан непосредственно в разделе переменных. m и n – это константы, их можно опустить и вставить конкретные значения, но лучше так не делать. Обычно подразумевают, что в интервале от 1 до m определяется количество строк, а в интервале от 1 до n – количество столбцов массива.
1 вариант – описание массива через раздел type:
2 вариант – описание массива в разделе переменных:
При использовании третьего варианта описания лучше сначала определить некоторый тип одномерного массива (строка двухмерного массива), который затем используется при описании двухмерного массива:
Для обращения к элементу двухмерного массива необходимо указать имя массива и в квадратных скобках через запятую – значения двух индексов (первый указывает номер строки, а второй – номер столбца), на пересечение которых стоит элемент (например, a[i,2]:=6). В языке программирования Pascal допустимо разделение индексов с помощью квадратных скобок (например, a[i][5]:= 7).
Если описывается двумерный массив как типизированная константа, то при задании значений его элементов он рассматривается как массив массивов. При этом в общих круглых скобках через запятую перечисляются заключенные в круглые скобки значения элементов строк (каждая строка в своих скобках):
Рассмотрим простой пример работы с двумерным массивом. Сначала заполним его данными, а затем выведем их на экран в виде таблицы.
Размерность массива (т.е. количество содержащихся в нем значений) определяется произведением количества строк на количество столбцов. В примере выше в массив помещается 15 значений.
Когда пользователь вводит очередное число, то процедура read считывает его и помещает в ячейку с текущими индексами i и j. Когда i равна единице, значение j меняется пять раз, и, значит, заполняется первая строка таблицы. Когда i равна двум, значение j снова меняется пять раз и заполняется вторая строка таблицы. Аналогично заполняется третья строка таблицы. Внутренний цикл for в общей сложности совершает 15 итераций, внешний только 3.
Как пользователь вводит значения – не важно. Он может их разделять либо пробелом, либо переходом на новую строку.
Вывод значений двумерного массива организован в виде таблицы. Выводятся 3 строки по 5 чисел в каждой. Внутри строк числа разделяются пробелом.
На самом деле, это не совсем корректно написанная программа. Мы несколько раз используем цифры 3 и 5. А что если мы захотим поменять размерность массива? Придется просмотреть всю программу (представьте, что она очень большая) и исправить значения. Это неэффективно. Поэтому в программе следует использовать константы. В случае чего их значения можно поменять всего лишь в одном месте.
Вторая проблема – это «кривость» выводимой на экран таблицы значений матрицы, в случае если есть значения разной разрядности (однозначное, двузначное и т.д. числа). Неплохо бы под каждое число отводить равное количество знаков.
Вот так может выглядеть подправленный вариант программы:
Последний урок паскаль был написан аж 7 марта, тогда мы разбирали одномерные массивы. Сегодня мы узнаем, что такое двумерный массив в паскале, как он описывается и что он из себя представляет. Подробнее далее.
Итак, что же такое двумерный массив? Для лёгкого восприятия представим одномерный массив как линию, а которой все элементы идут друг за другом горизонтально, а двумерный как квадрат, в котором элементы расположены как горизонтально, так и вертикально. Двумерный массив состоит из строчек и столбцов, их также называют матрицей или матричным массивом.
Как описываются двумерные массивы? Для записи двумерных массивов есть несколько способов, я рассмотрю 2 из них.
1 способ описание массива: array [1..m, 1..n] of тип переменных в массиве (integer/real/byte);
2 способ описания массива: array [1..m] of array [1..n] of тип переменных в массиве;
Сначала описываются строки (1..m), а потом столбцы (1..n).
Во втором способе описывается как бы два одномерных массива, которые вместе образуют один двумерный.
Двумерный массив может описываться в разделе Type, для последующего обращения к нему несколько раз или же в разделе описания переменных Var, хочу обратить внимание, что вместо m и n можно подставить и числа, а можно и пользоваться константами.
Пример задания двумерного массива в разделе описания переменных:
В этом случае мы задали двумерный массив a размера 100 на 100, то есть у нас получилась квадратная матрица.
Пример задания матричного массива при помощи раздела Type:
Во втором примере мы задали два одинаковых матричных массива размерами 100 на 100, при описании массива b нам не пришлось снова описывать его размеры и тип данных.
Как обращаться к ячейке-переменной двумерного массива?
Чтобы обратиться к двумерному массиву, нужно указать сначала номер строки, а потом номер столбца следующим образом:
Причём i и j может быть как переменными, так и целыми числами.
Пример записи данных в массив:
//присваивание ячейке с номером строки i и номером столбца j случайного значения
Мы заполнили массив случайными числами от 1 до 100.
Пример программы с использованием двумерного массива, в котором мы заполняем массив случайными числами и выводим его на экран:
Pascal-Паскаль
Программирование. Двумерные массивы Pascal-Паскаль
Программирование. Двумерные массивы Pascal-Паскаль
Двумерные массивы Паскаля – матрицы
Двумерный массив в Паскале трактуется как одномерный массив, тип элементов которого также является массивом (массив массивов). Положение элементов в двумерных массивах Паскаля описывается двумя индексами. Их можно представить в виде прямоугольной таблицы или матрицы.
Рассмотрим двумерный массив Паскаля размерностью 3*3, то есть в ней будет три строки, а в каждой строке по три элемента:
Каждый элемент имеет свой номер, как у одномерных массивов, но сейчас номер уже состоит из двух чисел – номера строки, в которой находится элемент, и номера столбца. Таким образом, номер элемента определяется пересечением строки и столбца. Например, a 21 – это элемент, стоящий во второй строке и в первом столбце.
Описание двумерного массива Паскаля.
Существует несколько способов объявления двумерного массива Паскаля.
Мы уже умеем описывать одномерные массивы, элементы которых могут иметь любой тип, а, следовательно, и сами элементы могут быть массивами. Рассмотрим следующее описание типов и переменных:
Пример описания двумерного массива Паскаля
Определение типов для двумерных массивов Паскаля можно задавать и в одной строке:
Основные действия с двумерными массивами Паскаля
Все, что было сказано об основных действиях с одномерными массивами, справедливо и для матриц. Единственное действие, которое можно осуществить над однотипными матрицами целиком – это присваивание. Т.е., если в программе у нас описаны две матрицы одного типа, например,
то в ходе выполнения программы можно присвоить матрице a значение матрицы b ( a := b ). Все остальные действия выполняются поэлементно, при этом над элементами можно выполнять все допустимые операции, которые определены для типа данных элементов массива. Это означает, что если массив состоит из целых чисел, то над его элементами можно выполнять операции, определенные для целых чисел, если же массив состоит из символов, то к ним применимы операции, определенные для работы с символами.
Ввод двумерного массива Паскаля.
Рассмотрим пример ввода двумерного массива Паскаля с клавиатуры:
Пример программы ввода двумерного массива Паскаля с клавиатуры
Двумерный массив Паскаля можно заполнить случайным образом, т.е. использовать функцию random (N), а также присвоить каждому элементу матрицы значение некоторого выражения. Способ заполнения двумерного массива Паскаля выбирается в зависимости от поставленной задачи, но в любом случае должен быть определен каждый элемент в каждой строке и каждом столбце.
Вывод двумерного массива Паскаля на экран.
Вывод элементов двумерного массива Паскаля также осуществляется последовательно, необходимо напечатать элементы каждой строки и каждого столбца. При этом хотелось бы, чтобы элементы, стоящие в одной строке, печатались рядом, т.е. в строку, а элементы столбца располагались один под другим. Для этого необходимо выполнить следующую последовательность действий (рассмотрим фрагмент программы для массива, описанного в предыдущем примере):
Пример программы вывода двумерного массива Паскаля
Замечание (это важно!): очень часто в программах студентов встречается ошибка, когда ввод с клавиатуры или вывод на экран массива пытаются осуществить следующим образом: readln (a), writeln (a), где а – это переменная типа массив. При этом их удивляет сообщение компилятора, что переменную этого типа невозможно считать или напечатать. Может быть, вы поймете, почему этого сделать нельзя, если представите N кружек, стоящих в ряд, а у вас в руках, например, чайник с водой. Можете вы по команде «налей воду» наполнить сразу все кружки? Как бы вы ни старались, но в каждую кружку придется наливать отдельно. Заполнение и вывод на экран элементов массива также должно осуществляться последовательно и поэлементно, т.к. в памяти ЭВМ элементы массива располагаются в последовательных ячейках.
Представление двумерного массива Паскаля в памяти
потребуется 12 байт памяти.
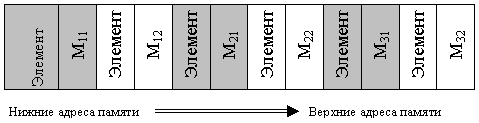
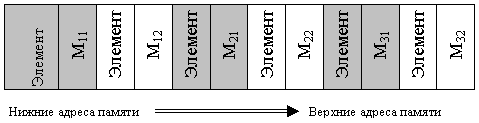
Как будут располагаться в памяти элементы этого массива? Рассмотрим схему размещения массива M типа matrix в памяти.
Под каждый элемент M [i,j] типа integer выделяется две ячейки памяти. Размещение в памяти осуществляется «снизу вверх». Элементы размещаются в порядке изменения индекса, что соответствует схеме вложенных циклов: сначала размещается первая строка, затем вторая, третья. Внутри строки по порядку идут элементы: первый, второй и т.д.
Как мы знаем, доступ к любой переменной возможен, только если известен адрес ячейки памяти, в которой хранится переменная. Конкретная память выделяется для переменной при загрузке программы, то есть устанавливается взаимное соответствие между переменной и адресом ячейки. Но если мы объявили переменную как массив, то программа «знает» адрес начала массива, то есть первого его элемента. Как же происходит доступ ко всем другим элементам массива? При реальном доступе к ячейке памяти, в которой хранится элемент двумерного массива, система вычисляет ее адрес по формуле:
Сколько памяти выделяется для массива?
Рассмотрим не столько вопрос о том, сколько памяти выделяется под массив (это мы разобрали в предыдущем разделе), а о том, каков максимально допустимый размер массива, учитывая ограниченный объем памяти.
Зачем нам это знать? Для того чтобы не удивляться, если при компиляции транслятор выдаст сообщение об ошибке объявления слишком длинного массива, когда в программе встретит описание (правильное с точки зрения синтаксиса):
Вы уже знаете, что, учитывая двухбайтовое представление целых чисел, реально можно объявить массив с количеством элементов равным 65536/2 –1=32767. И то лишь в том случае, если других переменных не будет. Двумерные массивы должны иметь еще меньшие границы индексов.
Примеры решения задач с двумерными массивами Паскаля
Задача: Найти произведение ненулевых элементов матрицы.
Решение:
обсудим сначала выполнение основной программы, реализацию процедур обговорим чуть позже:
А теперь поговорим о процедурах.
Замечание (это важно!) Параметром процедуры может быть любая переменная предопределенного типа, это означает, что для передачи в процедуру массива в качестве параметра, тип его должен быть описан заранее. Например :
Вернемся теперь к нашим процедурам.
Пример программы двумерного массива Паскаля
Программирование
Исходники Pascal (127)
Справочник
Справочник по паскалю: директивы, функции, процедуры, операторы и модули по алфавиту
Двумерные массивы паскаль
Двумерный массив в Паскале представляет собой таблицу, состоящую из нескольких одномерных массивов. Двумерные массивы Pascal называют матрицей. Положение элементов в матрице обозначается двумя индексами.
Рассмотрим матрицу 3*3, то есть она будет состоять из 3 строк и 3 столбцов:
Описание двумерного массива Паскаля.
Имеется ряд методов объявления двумерного массива.
Рассмотри способ, в котором указывается тип элемента и переменные.
Во втором и третьем способе матрицу можно задать в одну строку.
Основные действия с двумерными массивами Паскаля
Все основные действия над матрицами выполняются поэлементно, причем типы данных элементов должны быть одинаковыми. То есть, если матрица состоит из чисел, то действия можно выполнять только с числами. Однако для реализации операции присваивания массивам достаточно быть одного размера. Например, дан массив
в ходе выполнения такой программы матрице а можно присвоить значения матрицы b ( a := b ).
Ввод двумерного массива Паскаля.
Для поочередного ввода элементов в матрицу необходимо перебрать элементы с 1-го столбца 1-ой строки до последнего столбца последней строки. Для этого используется два оператора цикла for, причем один вложен в другой.
Проанализируем образец ввода двумерного массива Паскаля с клавиатуры:
Способ заполнения двумерного массива Паскаля зависит от поставленной задачи. Например, функцию random (N) позволяет заполнять матрицу случайными величинами a[i,j]:=random(25)-10. Некоторые задачи требуют содержание выражений в матрице. Не забывайте, что в любом случае должен быть определен каждый элемент в каждых строках и столбцах.
Вывод двумерного массива Паскаля на экран.
При выводе элементы должны печатать по порядку индексов, то есть в строках элементы стоят друг за другом, а в столбах один под другим. Для этого необходимо написать следующие элементы кода:
Представление двумерного массива Паскаля в памяти
В памяти ЭВМ элементы двумерного массива располагаются последовательно и занимают несколько байт. Например, элементы массива типа integer, будут занимать по 2 байта. А весь массив займет S^2 байта, где S – количество элементов в массиве.
В матрице для каждого элемента типа integer потребуется 2 байта памяти. Рассмотрим пример.
В данном случае необходимо 24 байт памяти.
Модель размещения массива M типа matrix в памяти.
Для любого элемента предоставляется две ячейки памяти, размещение осуществляется от первой строки до нижней, в порядке изменения индекса.
Между переменной и адресом ячейки устанавливается соответствие, однако, при объявлении матрицы программе известно только адрес начала массива, к остальным элементам адрес вычисляется по формуле:
Какой размер памяти выделяется для массива?
Рассмотрим пример, в котором:
С точки зрения синтаксиса запись верная, но компилятор выдаст ошибку об объявлении слишком длинного массива.
Можно без труда подсчитать количество элементов, которые допустимы по формуле: 65536/2 –1=32767. Однако, других переменных не должно быть. Матрицы обладают еще меньшими пределами индексов.
Решим задачу с двумерным массивом Паскаля.
Задача: Вычислить произведение ненулевых элементов матрицы.
Решение:
А теперь поговорим о процедурах.
Примечание! Тип массива должен быть определен заранее. Например:
Print – процедуры вывода на экран матрицы, которая передается по значению.
Итак, опишем ход выполнения программы.
Pascal: Занятие № 10. Двумерный массив в Pascal
Двумерный массив в Pascal
Матрица или двумерный массив – это прямоугольная таблица чисел (или других элементов одного типа). Каждый элемент матрицы имеет два индекса (номер строки и номер столбца).
Исходные данные для решения многих задач можно представить в табличной форме: 
Таблица результатов производственной деятельности нескольких филиалов фирмы может быть представлена так:
zavod1: array [1..4] of integer; zavod2: array [1..4] of integer; zavod3: array [1..4] of integer;
Или в виде двумерного массива так:
var A: array[1..3,1..4] of integer; begin
begin var a := new integer[3,4]; <. >end.
Описание, ввод и вывод элементов двумерного массива
Варианты описания двумерного массива (традиционный pascal)
const N = 3; M = 4; var A: array[1..N,1..M] of integer;
const M=10; N=5; type matrix=array [1..M, 1..N] of integer; var A: matrix;
for i:=1 to N do for j:=1 to M do begin write(‘A[‘,i,’,’,j,’]=’); read ( A[i,j] ); end;
for var i:=0 to a.RowCount-1 do for var j:=0 to a.ColCount-1 do a[i,j]:=readinteger;
var a := MatrRandomInteger(3,4,0,10); // целые числа в диапазоне от 0 до 10 var a1 := MatrRandomReal(3,4,1,9) // веществ. числа в диапазоне от 1 до 9
Следующий фрагмент программы выводит на экран значения элементов массива по строкам:
for i:=1 to N do begin for j:=1 to M do write ( A[i,j]:5 ); writeln; end;
begin var a := MatrRandomInteger(3,4,0,10); var a1 := MatrRandomReal(3,4,1,9); a.Println; a1.Println(6,1) // 6 позиций всего на вывод, 1 знак после десят. запятой end.
Рассмотрим следующую задачу: Получены значения температуры воздуха за 4 дня с трех метеостанций, расположенных в разных регионах страны:
| Номер станции | 1-й день | 2-й день | 3-й день | 4-й день |
|---|---|---|---|---|
| 1 | -8 | -14 | -19 | -18 |
| 2 | 25 | 28 | 26 | 20 |
| 3 | 11 | 18 | 20 | 25 |
Т.е. запись показаний в двумерном массиве выглядела бы так:
| t[1,1]:=-8; | t[1,2]:=-14; | t[1,3]:=-19; | t[1,4]:=-18; |
| t[2,1]:=25; | t[2,2]:=28; | t[2,3]:=26; | t[2,4]:=20; |
| t[3,1]:=11; | t[3,2]:=18; | t[3,3]:=20; | t[3,4]:=25; |
Или в pascalabc.NET:
var t := Matr(3,4,-8,-14,-19,-18,25,28,26,20,11,18,20,25); t.Println;
Объявление двумерного массива:
var t: array [1..3, 1..4] of integer;
Самостоятельно подумайте, как находится сумма элементов массива pascal.
Методы матриц для работы со строками и столбцами:
begin var a := MatrRandomInteger(3,4); a.Println; a.Row(0).Sum.Println(); a.Row(1).Average.Println; a.Row(2).Product.Println; a.Col(0).Min.Println; a.Col(1).Max.Println; end.
Главная и побочная диагональ при работе с двумерными матрицами в Pascal
Главная диагональ квадратной матрицы n x n (т.е. той, у которой количество строк равно количеству столбцов) проходит с верхнего левого угла матрицы (элемент 1,1) до правого нижнего угла матрицы (элемент n,n).
Побочная диагональ квадратной матрицы n x n проходит с нижнего левого угла матрицы (элемент n,1) до правого верхнего угла матрицы (элемент 1,n).
Формулу поиска элементов диагоналей проще всего искать, нарисовав элементы матрицы:
Если индексы начинаются с единицы (традиционный Паскаль):
| 1,1 | 1,2 | 1,3 | 1,4 |
| 2,1 | 2,2 | 2,3 | 2,4 |
| 3,1 | 3,2 | 3,3 | 3,4 |
| 4,1 | 4,2 | 4,3 | 4,4 |
Если индексы начинаются с нуля (pascalAbc.NET):
| 0,0 | 0,1 | 0,2 | 0,3 |
| 1,0 | 1,1 | 1,2 | 1,3 |
| 2,0 | 2,1 | 2,2 | 2,3 |
| 3,0 | 3,1 | 3,2 | 3,3 |
где n — размерность квадратной матрицы
Побочная диагональ матрицы в pascalAbc.Net имеет формулу:
n=i+j+1
где n — размерность квадратной матрицы
var i,j,n:integer; a: array[1..100,1..100]of integer; begin randomize; writeln (‘введите размерность матрицы:’); readln(n); for i:=1 to n do begin for j:=1 to n do begin a[i,j]:=random(10); write(a[i,j]:3); end; writeln; end; writeln; for i:=1 to n do begin for j:=1 to n do begin if (i=j) or (n=i+j-1) then a[i,j]:=0; write(a[i,j]:3) end; writeln; end; end.
var A:array[1..5,1..5] of integer; i,j:integer; sum,sum1,sum2:integer; begin randomize; for i:=1 to 5 do for j:=1 to 5 do A[i,j]:=random(10); write (‘Исходный массив A: ‘); for i:=1 to 5 do begin writeln; for j:=1 to 5 do write (A[i,j]:2,’ ‘); end; sum1:=0; for i:=1 to 5 do for j:=1 to 5 do if (i-j=1) then sum1:=sum1+A[i,j]; sum2:=0; for i:=1 to 5 do for j:=1 to 5 do if (j-i=1) then sum2:=sum2+A[i,j]; sum:=sum1+sum2; writeln; writeln(‘Сумма = ‘,sum); end.
Рассмотрим еще один пример работы с двумерным массивом.
var index1,index2,i,j,N,M:integer; s,min,f:real; a:array[1..300,1..300] of real; begin N:=10; M:=5; for i:=1 to N do begin for j:=1 to M do begin a[i,j]:=random(20); s:=s+a[i,j]; write(a[i,j]:3); end; writeln; end; f:=s/(N*M); writeln(‘srednee znachenie ‘,f); min:=abs(a[1,1]-f); for i:=1 to N do begin for j:=1 to M do begin if abs(a[i,j]-f)