Что такое материальная точка в технической механике

Материальная точка

Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.

Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи. [1]

При прямолинейном движении тела достаточно одной координатной оси для определения его положения.

Содержание

Особенности

Следствия

Ограничения

Ограниченность применения понятия о материальной точке видна из такого примера: в разреженном газе при высокой температуре размер каждой молекулы очень мал по сравнению с типичным расстоянием между молекулами. Казалось бы, им можно пренебречь и считать молекулу материальной точкой. Однако это не всегда так: колебания и вращения молекулы — важный резервуар «внутренней энергии» молекулы, «ёмкость» которого определяется размерами молекулы, её структурой и химическими свойствами. В хорошем приближении как материальную точку можно иногда рассматривать одноатомную молекулу (инертные газы, пары металлов, и др.), но даже у таких молекул при достаточно высокой температуре наблюдается возбуждение электронных оболочек за счёт соударений молекул, с последующим высвечиванием.

Примечания

Полезное

Смотреть что такое «Материальная точка» в других словарях:

МАТЕРИАЛЬНАЯ ТОЧКА — точка, имеющая массу. В механике понятием материальная точка пользуются в случаях, когда размеры и форма тела при изучении его движения не играют роли, а важна только масса. Практически любое тело можно рассматривать как материальную точку, если… … Большой Энциклопедический словарь

МАТЕРИАЛЬНАЯ ТОЧКА — понятие, вводимое в механике для обозначения объекта, к рый рассматривается как точка, имеющая массу. Положение М. т. в пр ве определяется как положение геом. точки, что существенно упрощает решение задач механики. Практически тело можно считать… … Физическая энциклопедия

материальная точка — Точка, обладающая массой. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика EN particle DE materialle Punkt FR point matériel … Справочник технического переводчика

МАТЕРИАЛЬНАЯ ТОЧКА — МАТЕРИАЛЬНАЯ ТОЧКА, понятие, вводимое в механике для обозначения тела, размерами и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Тело можно считать материальной… … Современная энциклопедия

МАТЕРИАЛЬНАЯ ТОЧКА — В механике: бесконечно малое тело. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910 … Словарь иностранных слов русского языка

Материальная точка — МАТЕРИАЛЬНАЯ ТОЧКА, понятие, вводимое в механике для обозначения тела, размерами и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Тело можно считать материальной… … Иллюстрированный энциклопедический словарь

материальная точка — понятие, вводимое в механике для объекта бесконечно малых размеров, имеющего массу. Положение материальной точки в пространстве определяется как положение геометрической точки, что упрощает решение задач механики. Практически любое тело можно… … Энциклопедический словарь

Материальная точка — геометрическая точка, обладающая массой; материальная точка абстрактный образ материального тела, обладающего массой и не имеющего размеров … Начала современного естествознания

материальная точка — materialusis taškas statusas T sritis fizika atitikmenys: angl. mass point; material point vok. Massenpunkt, m; materieller Punkt, m rus. материальная точка, f; точечная масса, f pranc. point masse, m; point matériel, m … Fizikos terminų žodynas

материальная точка — Точка, имеющая массу … Политехнический терминологический толковый словарь

Источник

Тема 1.1. Основные понятия и аксиомы статики

§1. Элементы векторной алгебры

В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.

1. Понятие вектора.

Операции над векторами. Вектора можно складывать и умножать на число.

— сумма двух векторов есть вектор

— существует нулевой вектор

Рис.1. Сложение векторов

В математике все вектора являются свободными, их можно переносить параллельно самим себе.

В сумме двух векторов (рис.1,а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис.1,б) получаем, что суммой нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.

Операции над векторами подчиняются следующим законам (см. рис.2):

Рис.2. Операции над векторами

2. Проекцией вектора на ось

Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону (см. рис.3).

Рис.3. Проекция вектора на ось

§2. Основные понятия статики

Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.

Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не де­формируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.

Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.

1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.

В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН). Сила является величиной векторной.

Ее действие на тело опре­деляется:

1) численной величиной или модулем силы

2) направле­нием силы

3) точкой приложения силы (рис.4).

Рис.4. Сила, приложенная к телу

Силу, как и другие векторные величины, изображают в виде направленного отрезка со стрелкой на конце, указывающей его направление.

Прямая DE, вдоль которой направлена сила, называется линией действия силы.

Понятия «линия действия» и «направление» близки, но не тождественны. Очевидно, что по линии действия можно определить направление с точностью до противоположного. Аналогично связаны понятия «модуль» и «величина» для вектора.

2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил. Предполагается, что действие силы на тело не изменится, если ее перене­сти по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.

3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, на­зывается свободным.

4. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состоя­ния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.

Например, если системы сил, изображенных на рис. 5, а и рис. 5, б, уравновешены, то эти две системы сил будут эквивалентны друг другу.

Рис 5. Система сил:

а – заданная система сил; б – эквивалентная система сил

5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или экви­валентной нулю.

7. Сила, равная равнодействующей по модулю, прямо противополож­ная ей по направлению и действующая вдоль той же прямой, назы­вается уравновешивающей силой.

8. Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.

9. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной.

Силы, действующие на все точки дан­ного объема или данной части поверхности тела, называются распре­деленными.

Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, пред­ставляют собою по существу равнодействующие некоторых систем распределенных сил.

В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равно­действующую сил тяжести его частиц. Линия действия этой равно­действующей проходит через точку, называемую центром тяжести тела.

§3. Аксиомы статики

Все теоремы и уравнения статики выво­дятся из нескольких исходных положений, принимаемых без матема­тических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁ = F₂) и направлены вдоль одной прямой в противоположные стороны (рис. 6).

Рис.6. Система сил, находящаяся в равновесии

Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равнове­сии не может.

Аксиома 2. Действие данной си­стемы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравнове­шенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсо­лютно твердое тело не изменится, если перенести точку при­ложения силы вдоль ее линии действия в любую другую точку тела.

Рис.7. Система сил

В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис.7). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю па­раллелограмма, построенного на этих силах, как на сторонах.

Рис.8. Равнодействующая двух сил

Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействую­щую, равную геометрической (векторной) сумме этих сил и прило­женную в той же точке.

Аксиома 4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но проти­воположное по направлению противодействие.

(рис. 9). Однако силы и не образуют урав­новешенной системы сил, так как они приложены к разным телам. Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме 4 рассматривается случай, когда силы приложены к разным телам и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме 2.

Рис.9. Противодействие

Рис. 10. Опирание балки на опоры:

а – схема загружения балки; б – силы действия балки на

опоры и противодействия со стороны опор на балку

Аксиома 5 (принцип отвердевания). Равновесие изме­няемого (деформируемого) тела, находящегося под действием дан­ной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сва­ренными друг с другом и т. д.

Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).

Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.

Видео-урок «Аксиомы статики»

§4. Связи и их реакции

По определению, тело, которое не скреплено с другими телами и может совершать из данного положе­ния любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.

Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.

Очень важен так называемый принцип освобождаемости, которым будем пользоваться в дальнейшем. Записывается он так:

Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.

Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.

Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равнове­сии, заменим стол силой, направленной вверх и равной, конечно, весу тела.

Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.

Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.

Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.

Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.

Рассмотрим, как направлены реакции некоторых основных видов связей:

1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпен­дикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.11, а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям сопри­касающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 11, б), то реакция направлена по нормали к другой поверх­ности.

Источник

Тема 1.6. Основные понятия кинематики

§1. Кинематика точки. Введение в кинематику.

Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Рис.1. Система отчета

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Основная задача кинематики точки твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих дан­ное движение.

Положение тела можно определить с помощью радиус-вектора или с помощью координат.

Рис.2. Радиус-вектор

Рис.3. Координаты точки М

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движе­нии все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом «тело» будем понимать «материальная точка».

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. Вид траектории зависит от выбора системы отсчета.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

где и — радиус-векторы тела в эти моменты времени.Единицы измерения в системе СИ: м (метр).

Модуль перемещения не может быть больше пути: ≤s.

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

Видео-урок «Механическое движение»

§2. Способы задания движения точки

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Рис.4. Движение точки М

При движении точки М вектор будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргу­мента t:

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.4), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

3. Естественный способ задания движе­ния точки.

Рис.5. Движение точки М

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О’, которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t).

§3. Вектор скорости точки

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения ∆r=v∆t, где v – постоянный вектор скорости.

Из соотношения видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени.

Источник

Теоретическая механика. В помощь студенту

Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.

Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.

Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.

Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.

Статика твердого тела

Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.

Основные понятия и законы статики

Кинематика

Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.

Основные понятия кинематики

Динамика

Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.

Основные понятия динамики

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

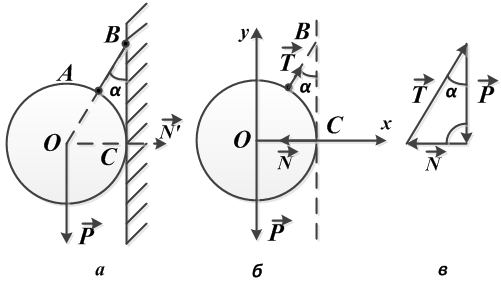
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.

Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).

Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:

После подстановки в формулы числовых значений, получим:
.

Ответ: .

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение траектории точки

Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.

Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
.

Опуская промежуточные выражения, получаем уравнение траектории:
.

Ответ: .

Решение примеров по теме: «Динамика»

Пример 3. Основной закон динамики точки

Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.

Решение.
Согласно основному закону динамики: .

Подставив значения в формулу, получим:

В помощь студенту

Формулы, правила, законы, теоремы, уравнения, примеры решения задач

Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.

Источник