Что такое материальная точка в физике кратко
Материальная точка
Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.
Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи. [1]
При прямолинейном движении тела достаточно одной координатной оси для определения его положения.
Содержание
Особенности
Следствия
Ограничения
Ограниченность применения понятия о материальной точке видна из такого примера: в разреженном газе при высокой температуре размер каждой молекулы очень мал по сравнению с типичным расстоянием между молекулами. Казалось бы, им можно пренебречь и считать молекулу материальной точкой. Однако это не всегда так: колебания и вращения молекулы — важный резервуар «внутренней энергии» молекулы, «ёмкость» которого определяется размерами молекулы, её структурой и химическими свойствами. В хорошем приближении как материальную точку можно иногда рассматривать одноатомную молекулу (инертные газы, пары металлов, и др.), но даже у таких молекул при достаточно высокой температуре наблюдается возбуждение электронных оболочек за счёт соударений молекул, с последующим высвечиванием.
Примечания
Полезное
Смотреть что такое «Материальная точка» в других словарях:
МАТЕРИАЛЬНАЯ ТОЧКА — точка, имеющая массу. В механике понятием материальная точка пользуются в случаях, когда размеры и форма тела при изучении его движения не играют роли, а важна только масса. Практически любое тело можно рассматривать как материальную точку, если… … Большой Энциклопедический словарь
МАТЕРИАЛЬНАЯ ТОЧКА — понятие, вводимое в механике для обозначения объекта, к рый рассматривается как точка, имеющая массу. Положение М. т. в пр ве определяется как положение геом. точки, что существенно упрощает решение задач механики. Практически тело можно считать… … Физическая энциклопедия
материальная точка — Точка, обладающая массой. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика EN particle DE materialle Punkt FR point matériel … Справочник технического переводчика
МАТЕРИАЛЬНАЯ ТОЧКА — МАТЕРИАЛЬНАЯ ТОЧКА, понятие, вводимое в механике для обозначения тела, размерами и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Тело можно считать материальной… … Современная энциклопедия
МАТЕРИАЛЬНАЯ ТОЧКА — В механике: бесконечно малое тело. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910 … Словарь иностранных слов русского языка
Материальная точка — МАТЕРИАЛЬНАЯ ТОЧКА, понятие, вводимое в механике для обозначения тела, размерами и формой которого можно пренебречь. Положение материальной точки в пространстве определяется как положение геометрической точки. Тело можно считать материальной… … Иллюстрированный энциклопедический словарь
материальная точка — понятие, вводимое в механике для объекта бесконечно малых размеров, имеющего массу. Положение материальной точки в пространстве определяется как положение геометрической точки, что упрощает решение задач механики. Практически любое тело можно… … Энциклопедический словарь
Материальная точка — геометрическая точка, обладающая массой; материальная точка абстрактный образ материального тела, обладающего массой и не имеющего размеров … Начала современного естествознания
материальная точка — materialusis taškas statusas T sritis fizika atitikmenys: angl. mass point; material point vok. Massenpunkt, m; materieller Punkt, m rus. материальная точка, f; точечная масса, f pranc. point masse, m; point matériel, m … Fizikos terminų žodynas
материальная точка — Точка, имеющая массу … Политехнический терминологический толковый словарь
Кинематика. Материальная точка.
Понятие «материальная точка» вводится для описания с помощью математических формул механического движения тел, поскольку описывать движение точки проще, чем реального тела, частицы которого, к тому же могут двигаться с разными скоростями.
Реальные движения тел довольно сложны, и изучая их возникает необходимость отвлечься от несущественных для данного движения деталей. С этой целью используют некоторые понятия, применимость которых определяется изучаемым движением.
Заменив тело материальной точкой, ей приписывают массу этого тела, пренебрегая его размерами, а вместе с этим и различием характеристик движения его точек.
Любое тело можно представить в виде материальной точки, если расстояния, проходимые телом, очень велики по сравнению с его размерами.
Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой. Слова «в данных условиях» означают, что при одних движениях тело можно считать материальной точкой, а при других – нет. Например, планеты при изучении их движения вокруг Солнца считаются материальными точками. Однако, решая задачи, связанные с суточным вращением планет, считать планеты материальными точками уже нельзя.
При поступательном движении тела, даже если его размеры сопоставимы с расстоянием, которое оно проходит, тело можно рассматривать в качестве материальной точки, поскольку все его точки движутся одинаково.
Материальная точка. Система отсчета
Урок 1. Физика 9 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Материальная точка. Система отсчета»
Неотъемлемой частью нашей жизни является движение. Движутся люди, автомобили, самолёты, космические корабли и планеты. Движутся молекулы, атомы, ионы и электроны. В окружающем нас мире все непрерывно изменяется. Как говорил древнегреческий философ Гераклит: «Все течёт, все изменяется. И невозможно дважды войти в одну и ту же реку».
Наиболее простой формой всех изменений является механическое движение. Механическое движение — это изменение положения одних тел относительно других в пространстве с течением времени.
А наука о закономерностях механического движения и причинах, вызвавших это движение, называется механикой.
Механику обычно разделяют на два раздела: кинематику, которая отвечает на вопрос, как движутся тела; и динамику, которая выясняет причины и проясняет, почему тела движутся именно так, а не иначе.
Изучение механики начинается с кинематики, так как понятия кинематики лежат в основе всей физики.
Кинематика — это раздел механики, который изучает движение тел без учёта причин, вызвавших это движение.
Основная задача кинематики заключается в нахождении положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.
В седьмом классе вы изучали самый простой вид движения —прямолинейное. В действительности движение тел может быть очень сложным: понаблюдайте за самолётом, который выполняет фигуры высшего пилотажа…
Каким образом кинематика может описать такие сложные движения?
Дело в том, что кинематика позволяет представить любое сложное движение, как состоящее из трёх основных.
Все вы знаете, что любое тело в каждый момент времени обладает некоторой геометрической формой, определённым образом ориентировано в пространстве и занимает в нем некоторое место. Проведём простой опыт с обыкновенным ластиком. Его можно изогнуть, то есть изменить его форму. Его можно повернуть, то есть по-другому сориентировать относительно стола. И, наконец, ластик можно перенести в другое место без изменения формы и ориентации в пространстве.
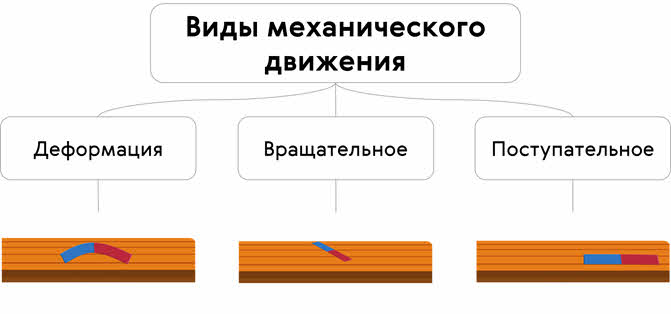
Значит, и форма, и ориентация в пространстве, и местоположение тела с течением времени могут изменяться. И каждому из этих изменений соответствует один из трёх основных видов механического движения — деформация…, вращательное движение… и поступательное движение…
С деформацией тела вы знакомы. Напомним, что это процесс изменения формы и (или) объёма тела. В результате этого процесса изменяется расстояние между точками тела.
Вращательное движение тела — это движение, при котором происходит изменение ориентации тела в пространстве (проще говоря, поворот тела).
Ну а перемещение тела без деформирования и поворота называется поступательным движением. При таком движении любая прямая, мысленно проведённая через любые две точки тела, остаётся параллельной самой себе.
Во многих задачах деформированием тела можно пренебречь. В таких случаях пользуются моделью абсолютно твёрдого тела — это тело, у которого расстояние между любыми его точками не меняется.
Если же в задаче, помимо деформации, можно пренебречь и вращением тела, то остаётся рассмотреть лишь его поступательное движение. А для таких задач достаточно изучить движение только одной точки тела, то есть использовать модель материальной точки.
Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.
Слова «в данных условиях» означают, что одно и то же тело при одних его движениях можно считать материальной точкой, при других — нет. Например, при изучении движения планет нашей Солнечной системы вокруг Солнца, их можно считать материальными точками, так как их размеры очень малы, по сравнению с расстояниями, которые они проходят.
Однако при рассмотрении задач, связанных с суточным вращением планеты, считать её материальной точкой нельзя, так как результат будет зависеть от размеров планеты, скорости движения её различных точек и так далее. Например, в Москве солнце встаёт на 7 часов раньше, чем в Нью-Йорке.
Поэтому, чтобы тело можно было принять за материальную точку, должно выполняться одно из трёх условий:
· тело движется поступательно;
· размеры тела много меньше расстояния, которое оно проходит;
· размеры тела много меньше расстояния до тела отсчёта.
Напомним, что тело отсчёта — это тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.
Вам известно, что одно и то же тело может двигаться относительно одних тел и одновременно оставаться неподвижным для других. Так пилот самолёта неподвижен относительно самолёта, но движется вместе с ним относительно земли. Таким образом, когда говорят о движении какого-либо тела, необходимо указывать тело, относительно которого это движение рассматривается.
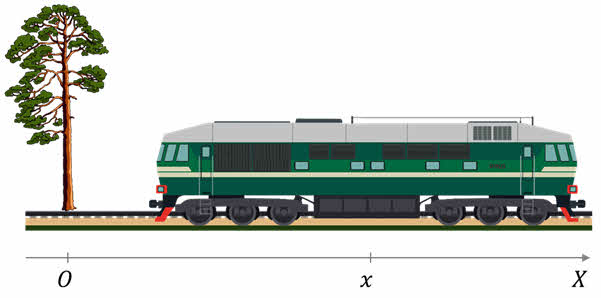
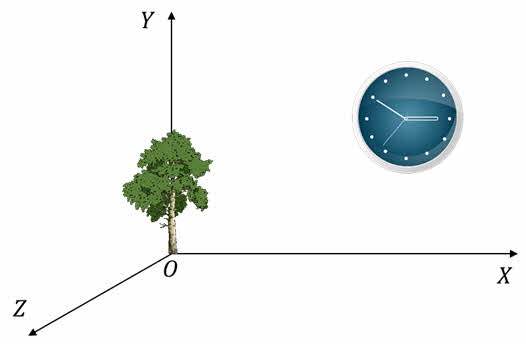
Положение тела в пространстве определяется с помощью координат. Например, рассмотрим движения локомотива по железной дороге. Его положение в любой момент времени можно задать одной координатой, например, Х. Для этого с телом отсчёта (например, это может быть дерево) связывается система координат, состоящая из одной координатной оси.
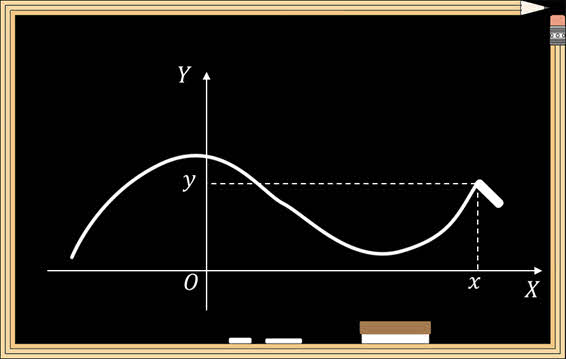
При изучении движения тела по плоскости, например, мела по школьной доске, одной координаты уже недостаточно. Поэтому, для описания такого движения следует использовать две взаимно перпендикулярные координатные оси и в каждый момент времени знать две координаты движущегося тела.
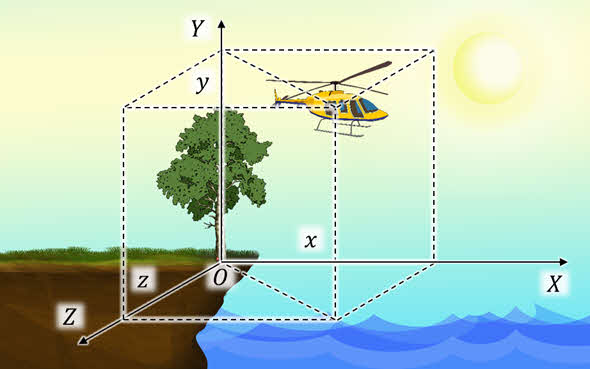
Когда же рассматривается движение тела в пространстве, например, движение вертолёта, то система координат, связанная с телом отсчёта, будет состоять из трёх взаимно перпендикулярных координатных осей: OX, OY, OZ.
А так, как при движении тела его координаты с течением времени изменяются, то необходимо иметь прибор для измерения времени.
Тело отсчёта, снабжённое устройствами для определения положения других тел и для измерения времени, называется системой отсчёта.
Мы будем использовать систему отсчёта, которая состоит из тела отсчёта, жёстко связанной с ним системы координат и часов.
Конечно, во многих случаях мы не можем непосредственно измерить координаты движущегося тела в любой момент времени. Например, мы не можем расположить линейку и расставить людей с часами вдоль многокилометрового пути движущегося мотоцикла, плывущего по морю корабля, летящего самолёта или космической ракеты, движение которых мы наблюдаем. Тем не менее знание законов физики позволяет нам определить координаты тел, движущихся в различных системах отсчёта.
А теперь давайте решим с вами одну небольшую задачку. Можно ли принять Землю за материальную точку при расчёте: расстояния от Земли до Солнца; пути, пройденного Землёй по орбите вокруг Солнца за месяц; длины экватора и скорости движения Земли по орбите вокруг Солнца?
Решение этой задачи не сложное. Здесь главное вспомнить, в каких случаях тело можно принимать за материальную точку, а в каких нет. И так, тело можно принять за материальную точку, если тело движется поступательно; если размеры тела много меньше расстояния, которое оно проходит; и, если размеры тела много меньше расстояния до тела отсчёта.
Рассмотрим случай а) более подробно. Для это проверим выполнение выше названных условий. Согласно первому условию, тело должно двигаться поступательно. Для нашего случая он не выполняется, так как о движении Земли в условии задачи ничего не говорится.
Второе условие материальной точки также не выполняется, так как мы не знаем расстояние, пройденное Землёй.
По третьему условию размеры тела должны быть намного меньше расстояния до тела отсчёта. В нашем случае, тело отсчёта — это Солнце. Среднее расстояние от Земли до Солнца составляет 149,6 миллионов километров, а средний радиус нашей планеты всего 6371 километр, что, конечно же, намного меньше среднего расстояния до Солнца.
Значит, в примере а) Землю можно принять за материальную точку, так как выполняется третье условие.
Далее рассуждая аналогично получим, что в примере б) Землю можно принять за материальную точку, так как её размеры много меньше расстояния, которое она проходит по орбите за месяц.
В примере в) Землю нельзя считать материальной точкой, так как при расчёте длины экватора Земли нельзя пренебречь её размерами.
И наконец в примере г) Землю можно считать материальной точкой, так как размеры Земли во много раз меньше среднего расстояния до Солнца.
Материальная точка
Для описания движения тела нужно знать, как движутся различные его точки. Однако в случае поступательного движения все точки тела движутся одинаково. Поэтому для описания поступательного движения тела достаточно описать движение одной его точки.
Также во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно описывать как точку.
Слово «материальная» подчеркивает здесь отличие этой точки от геометрической. Геометрическая точка не обладает никакими физическими свойствами. Материальная точка может обладать массой, электрическим зарядом и другими физическими характеристиками.
Одно и то же тело в одних условиях можно считать материальной точкой, а в других – нет. Так, например, рассматривая движение корабля из одного морского порта в другой, корабль можно считать материальной точкой. Однако, при исследовании движения шарика, который катится по палубе корабля, корабль считать материальной точкой нельзя. Движение зайца, убегающего по лесу от волка, можно описывать, приняв зайца за материальную точку. Но нельзя считать зайца материальной точкой, описывая его попытки спрятаться в нору. При изучении движения планет вокруг Солнца их можно описывать материальными точками, а при суточном вращении планет вокруг своей оси такая модель неприменима.
Важно понимать, что в природе материальных точек не существует. Материальная точка – это абстракция, модель для описания движения.
Примеры решения задач по теме «Материальная точка»
| Задание | Можно ли принять за материальную точку: а) автомобиль, въезжающий в гараж; б) автомобиль на трассе Москва-Ярославль? |
| Ответ | а) автомобиль, въезжающий в гараж нельзя принять за материальную точку, так как в данных условиях существенны размеры автомобиля; |
б) автомобиль на трассе Москва-Ярославль можно принять за материальную точку, так как размеры автомобиля намного меньше расстояния между городами.
| Задание | Указать, в каких из приведенных ниже случаях изучаемое тело можно принять за материальную точку: а) рассчитывают давление трактора на грунт; б) вычисляют высоту, на которую поднялась ракета; в) рассчитывают работу при поднятии в горизонтальном положении плиты перекрытия известной массы на заданную высоту; г) определяют объем стального шарика при помощи измерительного цилиндра (мензурки). |
| Ответ | а) при расчете давления трактора на грунт трактор нельзя принять за материальную точку, так как в данном случае важно знать площадь поверхности гусениц; |
б) при расчете высоты подъема ракеты, ракету можно считать материальной точкой, так как ракета движется поступательно и расстояние, пройденное ракетой. намного больше ее размеров;
в) в данном случае плиту перекрытия можно считать материальной точкой. так как она совершает поступательное движение и для решения задачи достаточно знать перемещение ее центра масс;
г) при определении объема шарика. шарик считать материальной точкой нельзя, потому что в данной задаче существенны размеры шарика.
| Задание | Можно ли принять Землю за материальную точку при расчете: а) расстояния от Земли до Солнца; б) пути, пройденного Землей по орбите вокруг Солнца; в) длины экватора Земли; г) скорости движения точки экватора при суточном вращении Земли вокруг оси; д) скорости движения Земли по орбите вокруг Солнца? |
| Ответ | а) в данных условиях Землю можно принять за материальную точку, так как ее размеры намного меньше расстояния от нее до Солнца; |
б) в данных условиях Землю можно считать материальной точкой, так как путь, который она проходит по орбите намного превышает ее размеры;
в) при измерении длины экватора Землю считать материальной точкой нельзя, потому что в данном случае имеют значения размеры Земли;
г) в данном случае Землю нельзя считать материальной точкой, так при измерении скорости движения точки экватора при суточном вращении планеты, важны размеры планеты и ее форма;
д) в данном случае Землю можно принять за материальную точку, так как размеры орбиты намного превосходят размеры Земли.
Эта абстрактная модель представляет собой идеальное тело, имеющее определённую массу, размеры которого не имеют значения и не принимаются во внимание.
Такое упрощение необходимо для более простого решения различных задач, связанных с механическим движением.
Физические основы механики
Физика — это наука о природе, изучающая наиболее простые и общие свойства, присущие материальному миру. Благодаря этому, она является универсальной базой для естествознания и техники, а также состоит из большого количества отдельных дисциплин — классической и квантовой механики, теории относительности, а также электродинамики, оптики и прочих.
Изучение физики начинается с механики — раздела, который рассматривает движение как изменение положения тела в пространстве с течением времени. Поэтому законы механики наиболее ясно выражают пространственно-временные отношения между объектами и событиями.
Основополагающие законы физики были в своё время установленны именно на основе наблюдения соответствующих явлений и экспериментов, из-за этого, за небольшим исключением, сфера их применения довольно ограничена. В частности, классическая механика распространяется лишь на медленное движение частиц и тел в макроскопических областях пространства. Перемещение на околосветовых скоростях подчиняется законам теории относительности, а свойствами микроскопических частиц занимается квантовая механика.
Классическая механика решает две основные задачи:
Решение первой задачи в своё время привело Исаака Ньютона к открытию общих принципов движения материальной точки — динамики. Вторая послужила установлению законов о сохранении импульса и энергии.
Модели и относительность
Физика относится к точным наукам — свои результаты она выражает не только на словах, но и с помощью математических соотношений и формул. Однако свойства физических тел и явлений настолько многогранны, что даже самая совершенная теория не в состоянии отобразить их во всей своей полноте. Поэтому вместо реальных объектов, наука предпочитает оперировать физическими моделями — идеализированными телами, которые отображают лишь существенные для рассмотрения явлений свойства и факторы.
В механике существует две основные модели:
Положение объекта в пространстве и его перемещение можно определить лишь относительно другого материального тела отсчёта и связанной с ним системой координат. Помимо этого, для описания движения необходимо пользоваться общепринятым и согласованным принципом фиксации моментов, а также иметь возможность проведения измерений временных промежутков во всех точках пространства.
Совокупность тела отсчёта, системы координат и неподвижного относительно неё хронометра называют системой отсчёта.
Таким образом, местоположение и перемещение любого объекта во вселенной может быть определено лишь относительно конкретной точки, от которой ведётся отсчёт. В то же время выбор системы отсчёта является произвольным и определяется лишь удобством для описания движения в заданных условиях. Отсюда следует, что положение объекта и его перемещение в пространстве является относительным по определению.
Понятие материальной точки
В отличие от геометрической точки, не имеющей никаких материальных свойств и обладающей лишь одной пространственной координатой, материальная может иметь массу, электрический заряд и прочие характеристики, необходимые для решения конкретной задачи.
Определение материальной точки в физике необходимо ввести для упрощения расчётов. Очевидно, что для описания движения такой абстрактной модели требуется минимальное количество вычислительных ресурсов.
Как правило, точке приписывается масса реального объекта, а остальные характеристики опускаются. Это можно делать лишь в том случае, когда перемещение, совершаемое наблюдаемым телом, несоизмеримо больше его размера. К примеру, для описания движения Земли по солнечной орбите совсем необязательно учитывать её вращение вокруг собственной оси.
Если возникла необходимость рассчитать среднюю скорость авиалайнера, следующего по определённому пути, форма его корпуса не имеет никакого значения. В таком случае самолёт являет собой пример материальной точки, которая должна пройти определённое расстояние за промежуток времени. Однако при нахождении показателя сопротивления воздуха летательный аппарат необходимо рассматривать как сложную систему.
При поступательном движении все элементы тела движутся в одном направлении, его можно принимать за точку
Несмотря на универсальность и удобство точечной модели, её применение имеет существенные ограничения. Это хорошо видно на примере разреженного газа при высокой температуре. Каждая молекула имеет очень маленький размер, несоизмеримый с путём, который она проходит в пространстве. Однако в этом случае молекулу далеко не всегда можно принять за точку. Дело в том, что колебание и вращение частиц перегретого газа создают своеобразный энергетический резервуар, и пренебрегать этими характеристиками в большинстве случаев нельзя.
Описание движения в кинематике
Кинематика — это начальный раздел механики, в котором устанавливаются понятия и величины, определяющие движение, общие соотношения между его характеристиками и способы описания. В разделе не рассматриваются условия и причины, определяющие характер движения тел. Поскольку любой предмет можно считать как систему идеальных моделей, прежде всего рассматривается кинематика одной точки.
Существует три способа описания движения и положения точки в выбранной системе отсчёта:
В классической механике для удобства используются инерциальные системы отсчёта. Их особенность заключается в том, что движение всех тел происходит равномерно и прямолинейно или же полностью отсутствует. Пространство и время в такой системе обладают изотропным и равномерным строением.
Динамика и законы Ньютона
Динамика — это раздел механики, в котором законы движения тел устанавливаются через причины, обусловливающие его характер. Основу раздела составляют 3 закона Ньютона, являющиеся обобщением результатов наблюдений и специально поставленных экспериментов. Их не получится вывести из каких-либо более простых принципов.
Законы динамики имеют важное практическое значение. На них основаны расчёты, по которым сооружаются всевозможных машины и механизмы, инженерные конструкции, космические аппараты и прочая техника.
Однако стоит заметить, что утверждения Ньютона не являются универсальными даже в рамках классической механики и выполняются лишь в инерциальных системах отсчёта.
Три закона Ньютона:
Законы Ньютона нельзя изолировать друг от друга, так как они — система органичных и взаимосвязанных утверждений. Они применяются для решения любой задачи динамики, но второй закон принято считать основным, поскольку он непосредственно оперирует основными характеристиками движения.
Для определения законов движения точки необходимо иметь достоверную и полную информацию о силах, действующих на неё.
В макроскопическом мире можно наблюдать большое количество всевозможных сил, которые являются проявлениями двух самых фундаментальных взаимодействий во вселенной — электромагнитного и гравитационного. Притяжение обусловлено гравитацией, а все остальные известные науке силы имеют электромагнитную природу.
Кратко ознакомившись с особенностями классической механики, можно понять, с какой целью используется понятие материальной точки. Нужно понимать, что физика не работают с реальными объектами, а лишь с абстрактными моделями. Это помогает облегчить теоретические построения и расчёты.