Что такое математический объект
Что такое математический объект
Беседа 4. Математические объекты
Математика, как и другие науки, изучает окружающий нас мир, природные и общественные явления, но изучает лишь особые стороны этих явлений.
В других случаях, кроме формы и размера, учитывают еще взаимное расположение частей фигуры.
Такие математические объекты, как числа, образуются путем выделения при рассмотрении различных совокупностей (множеств) однородных предметов таких общих свойств, как количество предметов в совокупности или их порядок следования, абстрагируясь от всех других свойств этих предметов (их неодинаковости, материала, цвета, величины и т. д.).
Итак, математика изучает особые идеальные математические объекты, которые образуются путем сложной мыслительной деятельности людей в процессе познания количественных свойств и отношений, а также пространственных свойств и форм предметов и явлений окружающего мира.
Поэтому первое, чему надо учиться в математике,- это умению в процессе изучения каких-то предметов или явлений для решения задач по определению количественной стороны или пространственных соотношений этих предметов или явлений образовывать, создавать математические объекты. Рассмотрим в качестве примера такую задачу.
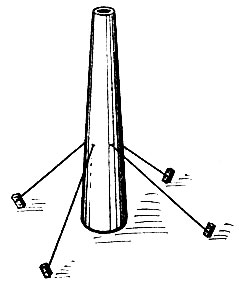
Задача.Для того чтобы укрепить железную дымовую трубу, было решено на высоте 20 м от ее основания прикрепить растяжки из стального каната, которые закрепить к четырем бетонным тумбам, находящимся на расстоянии 15 м от основания трубы. Сколько каната для этого потребуется? (Рис. 2.)
Рис. 2
Вообще надо помнить, что математическое решение любой практической задачи всегда является приближенным.
Для того чтобы закрепить полученные знания и проверить себя, как вы их усвоили, выполните следующее задание.
2.1. Какие геометрические фигуры выступают в качестве идеальных образов (моделей) реальных предметов в следующих практических задачах:
а)Найти площадь пятикопеечной монеты.
б) Найти длину обруча.
в) Найти площадь комнаты.
От каких свойств реальных предметов мы при этом абстрагируемся, а какие учитываем?
2.2. За билетами в театр стоит очередь. Какие математические объекты характеризуют положение (место) каждого человека в этой очереди? Какие практические задачи можно решить с помощью этих математических объектов?
2.3. Велосипедист выехал из города А в 9 ч утра и прибыл в город В, отстоящий от А на расстоянии 60 км, в 12 ч дня. Отдохнув в В 2 ч, он поехал дальше в город С, отстоящий от В на 72 км, и прибыл туда в 6 ч вечера.
Как можно наиболее просто и наглядно математически описать событие поездки велосипедиста из А в С? Какие практические задачи можно решить, имея это математическое описание? Какие математические объекты при этом использованы?
Единая природа математических объектов
В природе существует четыре основные первичные элементы структур, как составляющие десятирицы: монады, диады, триады и тетрады. В математике одни считают, что имеются скаляры, векторы и билинейные формы и тензоры, частными случаями последних являются все предыдущие. Другие представляют, что тензор обобщает понятия скаляра, вектора и матрицы и что привычные математические объекты лишь частные примеры более общего понятия, коим является тензор.
Кто прав? Чтобы разобраться в этом, необходимо выяснить физическую сущность математических объектов.
Математика вместе с языком, искусством и изобретательством образовывают систему мыслительной деятельности человека. Вместе с тем она сама является системой, так как содержит все присущие системам атрибуты.
Она существует в среде, которая является источником своего существования. Это можно представить, как множества с математическими объектами. В математике осуществляются какие-то операции, как аналог функционирования системы.
Она имеет свои фазовые состояния. У нее есть неопределенности, взаимодействия и преобразования. С ее помощью формулируются задачи, которые имеют решения, что аналогично органу саморегуляции в естественных системах или органу управления в искусственных системах.
Математика должна быть построена по образу и подобию естественных систем, тогда она будет способна предсказать то, что существует, но пока недоступно человеческому сознанию. Так оно, в принципе и есть, но не всегда и не везде.
Даже если математика построена на ложных физических принципах, то ее формулы работают, а теория создает некие фантастические конструкции. Так случилось и с теорией относительности, и с квантовой механикой.
Это свидетельствует о том, что законы в математике и в реальной действительности одни и те же, только сформулированы по-другому. Однако математика может «оторваться» от реальной действительности и изобрести такие конструкции, которые не существуют в реальности. В связи с этим возникает вопрос: а нужна ли человеку такая математика, которая ничего не отображает в настоящем и не может ничего отобразить в будущем?
Для того, чтобы такого не случалось, надо математику строить по законам естественного развития Природы. Прежде всего, необходимо рассмотреть единичные объекты Природы и их аналоги в математике, т.е. естественные количественные объекты и их меру.
Особенностью этих элементов является то, что каждый последующий содержит все предыдущие. Комплекс содержит два скаляра, вектор – три комплекса, в которых по два скаляра, тензор – четыре вектора, в которых по три комплекса, содержащих по два скаляра. Получается цепочка скаляров: 1-2-6-10 (рисунок). Это напоминает расположение электронов и орбит атома. Видимо не случайно.
Вообще говоря, в математике считается, что «те;нзор (от лат. tensus, «напряженный») — объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого». Или «тензор – это математический объект, который как объект не зависит от смены системы координат, но его компоненты при смене системы координат преобразуются по определенному математическому закону»
Здесь, очевидно, следует уточнить природу математических объектов. С одной стороны, меньшие образовывают большие, а большие распадаются на меньшие. Видимо, это не одно и то же. Два скаляра образуют комплекс, три комплекса – вектор, четыре вектора – тензор. А распадаются они в обратной последовательности. Поэтому, говорить о том, что меньшие являются частным случаем больших, вряд ли обоснованно.
Все структурные элементы могут существовать не только как самостоятельные целостные объекты, являясь элементами множеств, но и как среды (источники) существования систем.
Например, у естественных и технических систем таким источником является энергия, у производственных систем источником существования служат сырьевые ресурсы. Есть сырье – производство работает, нет сырья – производство стоит. Таких примеров много, где в качестве источника существования выступают, либо монады (скаляры), либо диады (комплексы), либо триады, (векторы) либо тетрады (тензоры).
Что такое математический объект
1. нБФЕНБФЙЮЕУЛЙК ПВЯЕЛФ ЛБЛ БВУФТБЛГЙС ПФ БВУФТБЛГЙЙ
чУЕ ЬФП, ВЕЪХУМПЧОП, УРТБЧЕДМЙЧП: Й ЧЩУПЛБС БВУФТБЛФОПУФШ, Й «ЦЕУФЛПУФШ», Й ПРПУТЕДПЧБООПУФШ. оП ЬФП ЕЭЕ ОЕ ЧУС РТБЧДБ П НБФЕНБФЙЛЕ.
дПУФБФПЮОП ПФЧМЕЮЕООПК УФЕРЕОЙ ПВЭОПУФЙ Й ДБЦЕ ЧУЕПВЭОПУФЙ ЧМБДЕАФ Й ОЕЛПФПТЩЕ ДТХЗЙЕ ОБХЛЙ. оЕ ФПМШЛП ЖЙМПУПЖЙС, Б ФБЛЦЕ ЖЙЪЙЛБ, МПЗЙЛБ. тБЧОП Й ИБТБЛФЕТЙУФЙЛБ «ЦЕУФЛПУФЙ». чППВЭЕ, ДЕМБС ЪБСЧМЕОЙС ПФОПУЙФЕМШОП ЖЙЪЙЮЕУЛЙИ ПВЯЕЛФПЧ, ОЕ РТЙИПДЙФУС ЗПЧПТЙФШ П РПУФПСОУФЧЕ УФТХЛФХТ Й ТБЪНЕТОПУФЕК, РПУЛПМШЛХ ОБ ЗТБОЙГБИ ФЕМ ОЕРТЕТЩЧОП УПЧЕТЫБАФУС РЕТЕНЕОЩ, РПДФБЮЙЧБАЭЙЕ ЙОЧБТЙБОФОХА УФТПЗПУФШ. фЕН ОЕ НЕОЕЕ Ч ПРТЕДЕМЕООЩИ ТБНЛБИ ЬФЙ ПВЯЕЛФЩ РТЙОЙНБАФУС УЕВЕФПЦДЕУФЧЕООЩНЙ. уЮЙФБЕФУС, ЮФП НБФЕНБФЙЮЕУЛЙЕ ПВЯЕЛФЩ Ч ОБЙВПМШЫЕК УФЕРЕОЙ ХДПЧМЕФЧПТСАФ ЪБЛПОХ ФПЦДЕУФЧБ, ЙВП ПОЙ ОБУФПМШЛП ПВТБВПФБОЩ НЩУМША, ЮФП ЙН ОЕ ПУФБЧМЕОП ЧПЪНПЦОПУФЙ ДМС ЛБЛЙИ ВЩ ФП ОЙ ВЩМП ЙЪНЕОЕОЙК. оП ЧПФ, ЮФП ПФНЕЮБЕФ м.чЙФЗЕОЫФЕКО.
чПЪШНЕН УФТПЛХ, УПУФБЧМЕООХА ЙЪ УФБ НЙММЙПОПЧ НБФЕНБФЙЮЕУЛЙИ ЪОБЛПЧ. б ЪБФЕН ЧЕТОЕНУС Л ОЕК, УЛБЦЕН, ЮЕТЕЪ ПДЙО ЮБУ. тБЪЧЕ ПОБ ЪБ ЬФП ЧТЕНС ОЕ НПЦЕФ ЙЪНЕОЙФШУС? чЕДШ УФТПЛБ У РПДПВОЩН ЛПМЙЮЕУФЧПН ЪОБЛПЧ ОЕПВПЪТЙНБ ЪБ ХЛБЪБООЩК УТПЛ ЧТЕНЕОЙ. йОБЮЕ УЛБЪБФШ, УЧЕТИДМЙООЩЕ УФТПЛЙ ЪОБЛПЧ ПЛБЪЩЧБАФУС ОЕЦЕУФЛЙНЙ Й РПФПНХ Л ОЙН ОЕ ДПМЦОП ВЩФШ ДПЧЕТЙС. уМЕДПЧБФЕМШОП, Й РП РБТБНЕФТХ «ЦЕУФЛПУФЙ» НБФЕНБФЙЮЕУЛЙЕ ПВЯЕЛФЩ ПФМЙЮБАФУС ПФ ПВЯЕЛФПЧ, У ЛПФПТЩНЙ ПРЕТЙТХАФ ДТХЗЙЕ ОБХЛЙ, Ч МХЮЫЕН УМХЮБЕ МЙЫШ ЛПМЙЮЕУФЧЕООПК НЕТПК.
оБЛПОЕГ, УЧПКУФЧП НБФЕНБФЙЛЙ РТЕДУФБЧМСФШ ПРПУТЕДПЧБООПЕ ПФОПЫЕОЙЕ Л НЙТХ. ч ЬФПН ПУПВПК РТЙЧЙМЕЗЙЙ Х ОЕЕ ОЕФ. мАВБС ОБХЛБ, ЕУМЙ ПОБ ЦЕМБЕФ ВЩФШ ФЕПТЕФЙЮЕУЛПК, БДТЕУХЕФ УЧПЙ ЧЩУЛБЪЩЧБОЙС ТЕБМШОПУФЙ ОЕ РТСНП, Б ЮЕТЕЪ ЛПОГЕРФХБМШОЩЕ УЙУФЕНЩ, ДПВЩФЩЕ МПЗЙЛП-ЗОПУЕПМПЗЙЮЕУЛПК ТЕЛПОУФТХЛГЙЕК ЮХЧУФЧЕООП ДБООПЗП. фБЛ, Ч ЛМБУУЙЮЕУЛПК НЕИБОЙЛЕ НБФЕТЙБМШОЩЕ ФЕМБ РТЕДУФБЧМЕОЩ ЙДЕБМЙЪЙТПЧБООЩНЙ ПВТБЪБНЙ НБФЕТЙБМШОЩИ ФПЮЕЛ Й БВУПМАФОП ФЧЕТДЩИ ФЕМ. ч ЕЭЕ ВПМШЫЕК УФЕРЕОЙ ФЕПТЕФЙЮОЩ Й ПРПУТЕДПЧБОЩ РПОСФЙС ОЕЛМБУУЙЮЕУЛПК ЖЙЪЙЛЙ.
фЕРЕТШ ЧПЪШНЕН НБФЕНБФЙЮЕУЛПЕ РПОСФЙЕ. оБРТЙНЕТ, ЮЙУМП, РТЙФПН, ЧОБЮБМЕ ОЕ БВУФТБЛФОПЕ ЮЙУМП ЧППВЭЕ, Б ЛПОЛТЕФОПЕ: 5, 7, 8 12 Й Ф.Д.
лПОЕЮОП, БВУФТБЛГЙЙ, (ЛБЛ Й БВУФТБЛГЙЙ ВПМЕЕ ЧЩУПЛЙИ РПТСДЛПЧ) ЙНЕАФ НЕУФП Й Ч ДТХЗЙИ ОБХЛБИ. лТПНЕ ФПЗП, РПУМЕДОЙЕ ПРЕТЙТХАФ Й НБФЕНБФЙЮЕУЛЙНЙ ПВЯЕЛФБНЙ (ПУПВЕООП ЖЙЪЙЛБ). оЕ ЪОБЮЙФ МЙ ЬФП, ЮФП Х НБФЕНБФЙЛЙ ОЙЛБЛПК УРЕГЙЖЙЛЙ ОЕФ?
дЕМП Ч ФПН, ЮФП УПВУФЧЕООП НБФЕНБФЙЮЕУЛЙК РПДИПД ПФМЙЮБЕФУС ПФ ПУФБМШОЩИ ОБХЛ. фБЛ Ч УМХЮБЕ У ЮЙУМБНЙ. пРЕТЙТХС У УПЧПЛХРОПУФСНЙ ЛПОЛТЕФОЩИ ПВЯЕЛФПЧ Й УФБЧС ЙИ Ч ПДОП-ПДОПЪОБЮОПЕ УППФЧЕФУФЧЙЕ (ФП ЕУФШ ПВТБЪХС НБФЕНБФЙЮЕУЛХА БВУФТБЛГЙА ЮЙУМБ), НБФЕНБФЙЛ ОЕ БОБМЙЪЙТХЕФ УЧПКУФЧБ ЧИПДСЭЙИ Ч УПЧПЛХРОПУФЙ ПВЯЕЛФПЧ. пО ВЕТЕФ Ч ЛБЮЕУФЧЕ ЙУИПДОПК БВУФТБЛГЙЙ УБНЙ УПЧПЛХРОПУФЙ, ЪДЕУШ ЧБЦОП ОЕ «ЮФП», Б «УЛПМШЛП». фП ЕУФШ Ч БМЖБЧЙФ НБФЕНБФЙЮЕУЛПЗП СЪЩЛБ ЧЛМАЮБАФУС ПВЯЕЛФЩ ОЕ ОЙЦЕ РЕТЧПЗП ФЙРБ (ЛМБУУЩ, ЛМБУУЩ ЛМБУУПЧ Й Ф.Д.). ч ДТХЗЙИ ЦЕ ОБХЛБИ БМЖБЧЙФ УПУФБЧМЕО ЙЪ ПВЯЕЛФПЧ ОХМЕЧПЗП ФЙРБ (ЧЕЭЙ). рПДТПВОЕЕ ПВ ЬФПН Ч УЧСЪЙ У ФЕПТЙЕК ФЙРПЧ в. тБУУЕМБ (ЗМ. V, 4). бОБМПЗЙЮОП ФПЮЛБ Ч ЖЙЪЙЛЕ ИПФС Й ОЕ ЙНЕЕФ ЙЪНЕТЕОЙК, ОП ПВМБДБЕФ НБУУПК, НБФЕНБФЙЮЕУЛБС ЦЕ ФПЮЛБ ОЕ ОБДЕМЕОБ ОЙЛБЛЙНЙ ЖЙЪЙЮЕУЛЙНЙ УЧПКУФЧБНЙ. уЧПКУФЧП ЦЕ ТБЪНЕТОПУФЙ РХФЕН РТЕДЕМШОПЗП РЕТЕИПДБ УЧЕДЕОП Л ОХМА.
Как описать весь мир с помощью математики?
Древнегреческие философы Пифагор и Платон считали, что математика отражает глубинную структуру бытия, и с ее помощью можно описать то, как мир устроен на самом деле. Однако со времен Канта и до недавнего времени господствовал иной взгляд на науку и познание: считалось, что наш разум меняет изучаемый объект, подстраивая его под себя, и тем самым конструирует его. Неожиданным образом в наши дни философия вернулась к давней идее математической структуры мира, не зависящей от нашего сознания и познания. О том, как это вышло и что из этого следует, рассказывает философ Елена Косилова.
В последнее время философы много говорят о новом онтологическом повороте: это не могло не коснуться и философии математики. В ней всегда в том или ином виде спорят реализм и конструктивизм. Реализм древнее, он идет от Пифагора и Платона. Согласно реалистам, математические объекты существуют независимо от математика. Это согласуется со здравым смыслом, когда мы думаем о простых математических объектах, таких как прямая, треугольник или натуральный ряд. Скорее всего, есть основания говорить, что независимо от нас существует число π. Но существуют ли «сами по себе» интегралы или функция y = x2?
Конструктивизм, в отличие от платонизма, постулирует, что любые математические понятия рождаются только в умах людей и в их культуре. Имеет смысл (как в средневековье) выделять крайний реализм, умеренный реализм и крайний конструктивизм, который, соответственно, можно возвести к средневековому номинализму. Тогда крайний реализм будет выглядеть так:
Любые математические объекты существуют в независимом от человека математическом мире.
Мы открываем, а не изобретаем их.
Любые математические объекты сконструированы людьми. Если бы человеческие обстоятельства сложились по-другому, были бы придуманы другие объекты, и даже известные нам объекты обладали бы другими свойствами.
В Средние века об общих понятиях номиналисты говорили flatus vocis — колебания воздуха, «всего лишь слова».
Умеренный реализм — и он же умеренный конструктивизм:
Мы конструируем математические объекты, но в согласии с независимыми от нас логическими правилами.
Свойства сконструированного объекта не придумываются, а открываются.
Возможно, близким к умеренному конструктивизму счел бы себя Аристотель (хотя это, конечно, не факт).
Скептицизм в философии науки ХХ века
В философии со времени Канта господствовала теория познания. Из теории познания вычленилась философия науки, а в философии науки к концу XX века стали преобладать скептические направления — радикальный конструктивизм, социальный конструктивизм, учение о науке как практике и т.п. Радикальный конструктивизм начался с Канта, потому что его учение утверждало не только ограниченность наших познавательных способностей, но и активность познающего субъекта. С тех пор повелось считать, что субъект конструирует большую часть того, что познает. Учения о том, как именно субъект конституирует познаваемое и что в него привносит, становились все изощреннее.
Однако наука тем временем шла вперед широким шагом.
В современном мире мы не просто видим успехи науки — мы живем на ее иждивении и шагу не можем сделать без смартфона, компьютера и интернета.
Философы, относящиеся к науке свысока, настолько неадекватны с ее точки зрения, что развод философии с современной наукой уже приобрел черты скандала. Очень многие ученые презирают философию, потому что она не сообщает им ничего полезного. Философия конца XX века полностью промахивается мимо науки.
Но вот появляется новый реализм, новый материализм, происходит онтологический поворот. Из новых реалистов наиболее влиятелен Квентин Мейясу: в 2006 году вышла его книга «После конечности», которая уже успела стать знаменитой. В ней выдвигается два ошеломительных для философии тезиса: во-первых, вещь в себе познаваема, во-вторых, законы реальности совершенно случайны — такую случайность Мейясу называет контингентностью.
Учение о не познаваемости вещи в себе Мейясу называет корреляционизмом. Он имеет в виду, что, согласно современной философии, всякий объект, с которым мы имеем дело, всегда находится «в корреляции» с нами самими, с нашими познавательными способностями, с нашей мыслью об этом объекте, то есть речь идет все о том же конструировании. Корреляционизм начался с Канта, это он сопоставил каждую вещь с тем, как она нам является. Мейясу обвиняет корреляционизм в том, что он ставит себя в такое положение, что ему нельзя ничего возразить: ведь каждая мысль, которая может быть выдвинута против него, уже коррелирует с субъектом, находится внутри его познавательных способностей. Философ называет это кругом корреляционизма.
Спасение от торжества субъективности Мейясу видит в математике. С его точки зрения, на математику не распространяются трансцендентальные (корреляционистские) ограничения. Это у него постулат, обосновать его невозможно.
Кант считал, что математика априорна, она основана на общих познавательных способностях всех людей, фактически она является как раз изучением этих самых способностей.
Правда, Кант отводил основополагающую роль созерцанию, от которого современная математика ушла очень далеко. Но нельзя же всерьез доказывать, что человек способен познать нечто, выходящее за пределы его познавательных возможностей. Впрочем, это тавтология. Мейясу ничего не говорит об устройстве реальности, но мы поговорим позже о том, какая именно реальность имеется здесь в виду и как она соотносится с мышлением.
Вот что пишет Мейясу (выделение его):
«Вместо того, чтобы утверждать, что математика и физика имеют отношение только к априорным формам нашего опыта, я убежден … что нужно утверждать, подобно Декарту, что математика и математизированная физика дают нам средства для идентификации свойств мира, который радикально независим от мысли».
Это очень важная идея для Мейясу. Напрямую она не связана с его философией математики, она касается физики. Речь идет о том, что все природные законы могут изменяться. Все, кроме математики, совершенно ненадежно. Мы не только не знаем заранее, какой закон будет вскоре открыт, но и открытые законы могут завтра измениться. Мейясу не случайно осуждает Канта за антропоцентризм и одобряет Юма: таким образом он превозносит эмпиризм (хотя и не использует этого слова), причем эмпиризм скептический и как бы возведенный в квадрат: невозможно точно предсказать не только то или иное явление, но невозможно даже предсказать, сохранится тот или иной закон или нет.
У Мейясу очень сложные отношения с логикой. В одном месте он прямо говорит, что любые логические законы могут в любой момент поменяться, то есть они контингентны.
«Все что угодно может вполне реально обрушиться — и деревья, и звезды, и физические, и логические законы. Но не в силу некоторого вышестоящего закона, обрекающего любую вещь на исчезновение, но наоборот — в силу отсутствия такого вышестоящего закона, который способен был бы предотвратить исчезновение чего бы то ни было». Таким образом, можно подумать, что Мейясу считает логику такой же контингентной наукой, как физика.
Критика идей Мейясу
Это критика той части его философии, которая непосредственно связана с наукой.
Прежде всего, на мой взгляд, Мейясу не вполне понимает соотношение математики и логики, да и саму природу логики. Каким образом законы логики могут быть контингентными, если математика надежна? Математика основывается на логике. Даже согласно самой идее контингентности она должна, конечно, касаться эмпирических вещей, а не нормативной науки. Но если Мейясу хочет добиться непредсказуемости вообще всего, то можно и логику объявить контингентной — только тогда не надо объявлять надежной математику. Если изменятся, например, принципы следования, закон модус поненс, определения связок — то и равенства в математике, а также правила математического вывода станут совершенно другими. Скорее всего такое просто невозможно представить, это будет уже какая-то совершенно нечеловеческая логика и нечеловеческая математика.
Я понимаю задачу Мейясу по-другому: он хочет оправдать торжество современной науки, а не провозгласить новую нечеловеческую науку. Контингентность логики — это упущение Мейясу.
Теперь сосредоточимся на том, насколько представима контингентность физики. Мыслить ее можно широко, если не знать о ее очень тесной связи с математикой. Например, есть закон гравитационного притяжения двух тел: F = γm1m2 / R2. В нем сказано, что сила притяжения прямо пропорциональна массе каждого из этих тел и обратно пропорциональна квадрату расстояния. Что она возрастает с возрастанием массы, нам интуитивно кажется достаточно естественным. А что она убывает в зависимости от квадрата расстояния, казалось бы, установлено чисто эмпирически. Почему не в зависимости от первой степени расстояния или от его куба? Я была очень удивлена, когда мне объяснили, что на самом деле никакой другой степени тут не может быть — квадрат здесь потому, что пространство трехмерно. Другими словами, этот закон можно было не открывать эмпирически (хотя он открыт эмпирически). Его можно было буквально вывести из головы.
И в физике едва ли не все так. Только константы устанавливаются чисто эмпирически и могли бы быть совершенно другими.
Иногда физики пишут, что значения констант не случайно стали такими, чтобы появилась именно наша вселенная и в ней появились мы.
Что это так называемая тонкая настройка (fine tuning), которую разумный Творец вселенной подобрал специально. Однако понятно, что доказать это нельзя, можно только размышлять об этом.
Сама же структура физических законов чисто математическая. Многие знаменитые физики не уставали удивляться этому. Широко известна статья великого физика Юджина Вигнера «Непостижимая эффективность математики в естественных науках». В ней он пишет о том, что многие математические теории были разработаны неэмпирически, в виде, так сказать, чисто математической игры ума, а потом оказались на удивление пригодными для описания природных явлений. Например, тригонометрические функции были введены для описания треугольников. Но потом оказалось, что с помощью них можно описывать, например, законы протекания тока в цепи с емкостью и индуктивностью. В этой цепи нет никаких треугольников! Но ток течет почему-то согласно отвлеченным математическим принципам. Или то, что небесные тела движутся по орбитам, которые могут быть представлены как конические сечения — это опять-таки связано со структурой пространства.
В солнечной системе нет никаких конусов, но мы снова видим, что математические представления работают в физике, и работают достаточно неожиданным, неочевидным образом.
Вигнер приводит другие, не менее впечатляющие примеры. Не случайно сегодня едва ли не большинство законов физики рождаются на кончике пера, и перо это математическое.
Отсюда следует, что при постулировании надежности математики не следует говорить об абсолютной контингентности физики.
Такая центральная роль математики в науке о мироздании определенно взывает к появлению новой онтологии. Мы уже выяснили, что новая гносеология — это реализм, эмпиризм. Это то, что касается вопроса о познании человеком законов вселенной. Законы, конечно, устанавливаются эмпирически, но записываться они должны на математическом языке.
О каком же устройстве вселенной идет речь?
Предустановленная гармония
Но сначала два слова о том, что говорили о взаимодействии математики и физики до реалистических онтологий. Историк физики Владимир Визгин написал статью «Догмат веры физика-теоретика». Вообще там в основном идет речь о религиозном чувстве у физиков, но он много пишет о предустановленной гармонии между математикой и физикой. Автор «необъяснимой эффективности» Вигнер тоже намекал на предустановленную гармонию. Более того, этими же словами говорил Давид Гильберт («Естествознание и логика»). Наконец, очень похожие мысли высказывал Поль Дирак. Предустановленная гармония — не онтологическое учение, хотя само это понятие ввел Лейбниц в контексте онтологии своих монад. Но у вышеупомянутых физиков речь шла о ситуации в их науке. Они не говорили об устройстве вселенной.
Неопифагореизм
Что же получится, если сейчас начать говорить так о вселенной? Это будет учение о том, что вселенная устроена согласно математическим законам, то есть, иными словами, новый пифагореизм. Здесь некоторые из авторов, пишущие о новом реализме, вспоминают кроме Мейясу физика Макса Тегмарка. Мейясу чувствовал, к чему идет дело, и специально сообщил, что он не пифагореец. А Тегмарк уже открытым текстом описывает математическую вселенную и вспоминает Пифагора. Его статья, посвященная этому, так и называется, «Математическая вселенная». В ней он пишет: «После того, как Вигнер написал свое эссе 1967 года, стандартная модель физики частиц обнаружила новый „непонятный “ математический порядок в микрокосме элементарных частиц и в макрокосме ранней Вселенной. Я не знаю другого убедительного объяснения этой тенденции, кроме того, что физический мир действительно полностью математичен».
«Если моя жизнь в физике чему и научила меня, так это тому, что Платон был прав: благодаря современной физике стало очевидным, что конечная природа реальности не такова, какой кажется», — пишет Тегмарк в книге «Наша математическая вселенная», которая получила широкую известность среди физиков.
Тегмарк проводит капитальное математическое изучение условий, при которых вселенную можно считать математической структурой. Физические интерпретации он называет багажом и не вводит их в рассмотрение. Но никакой контингентности у него нет, потому что есть мультиверс. Условие множественности вселенных таково: если наблюдатель внутри вселенной (лягушка) описывает ее более сложным образом, чем наблюдатель извне, видящий четыре измерения (птица), то вселенные множественны. Поскольку фундаментальные законы извне вроде бы проще тех, что внутри, то он уверен, что вселенных много. И все математически допустимые физические варианты где-то, вероятно, реализуются.
Так выглядит онтология с точки зрения современных философствующих физиков. Думаю, французские новые реалисты должны встроиться в это русло и принять пифагореизм и теорию математической вселенной. Это не отменяет того, что конкретно в нашей вселенной законы могут оказаться любыми, хотя у физиков пока, конечно, не идет речь о контингентности внутри одной вселенной. Здесь мысль Мейясу носит более прорывной характер, чем у физиков, но, как уже говорилось, ему надо скорректировать учение о том, что контингентно абсолютно все, описываемое физически. Ему следует привести это в соответствии с необходимой стабильностью математики.
Тождество бытия и мышления
Что можно сказать о том, какое гносеологическое учение должно прийти на смену корреляционизму в этой новой для нас ситуации возрождения Пифагора (и Галилея)?
Поскольку математика теперь становится одновременно и наукой, и принципом устройства вселенной, то это с необходимостью требует только одного: тождества бытия и мышления.
Мы встречали такое положение у Парменида, у Спинозы («порядок идей соответствует порядку вещей»), у Гегеля. Оно всегда казалось нам экстравагантным. Теперь мы замечаем, что приходится его вводить уже в связи с деятельностью ученых. Конечно, полного тождества любого бытия с любым мышлением нет, «лягушачье» бытие случайно, человеческое мышление приводит к ошибкам. Однако мы видим вот что: по большому счету, в высших своих проявлениях мышление человека — это его работа в математике и логике. Речь идет не о построении гипотез и моделей, а о мышлении, в котором человек соприкасается со структурой самого мироздания.
Вопрос о материи и о точности
В богословских терминах (что чрезвычайно далеко от Мейясу, позиционирующего себя как антифидеиста) пифагорейскую теорию можно сформулировать так: Бог сотворил математику и некоторое количество материи. Поэтому материя подчиняется математическим законам. Что-то им должно подчиняться, в чем-то они должны воплощаться. Таким образом, мы выходим из пифагореизма в теорию Аристотеля о формах и материи.
Существенным у Аристотеля было то, что материя вообще не имела свойств, она не вносила ничего своего и ничего не искажала, поэтому формы можно было выделить вполне точно.
Остается вопрос, можно ли назвать теорию Аристотеля дуализмом формы и материи, если материя только «есть», и ничего больше о ней сказать нельзя. На мой взгляд, это дуализм, но тут можно рассуждать по-разному.
В истории философии было много дуалистических учений, где материи явным образом приписываются те или иные свойства. В учении Декарта материя уже обладает полным набором свойств. Не факт, что такой тип дуализма будет востребован в онтологии будущего. А вот аристотелевский дуализм, как мне кажется, очень подходит для современных учений, которые выделяют структуру отдельно от ее воплощения. И именно материя ответственна за воплощение структуры и представление ее в реальности.
Тегмарк формулирует эту идею следующим образом: чтобы описать математическую структуру вселенной, нам надо мысленно избавиться от так называемого багажа. Под багажом понимается конкретное воплощение структуры. В некотором смысле у Тегмарка получается, что багажом является материя. Однако он имеет в виду не это, а то, что багаж мешает выделять структуры. Он отвлекает внимание на себя. А это значит, что у него есть собственное бытие, то есть, скорее всего, какая-то своя структура.
Теперь мы можем сказать, почему математические структуры часто реализуются на практике с приблизительностью: это дает о себе знать материя.
Материя как идеальное мыслимое начало свойств не имеет. Но на практике она вносит шум. «Математическую точность не во всем нужно одобрять, но только в том, что не имеет материи» (Аристотель, Метафизика, 2, 3). А раз она что-то делает, значит, хоть какие-то свойства у нее есть. Также, скорее всего, следует сказать, что в ней воплощается одновременно много структур разного масштаба. Это делает общее описание процессов в материи сложным. Однако нельзя сказать, что оно перестает от этого быть математическим. Тегмарк увязывает свою картину математической вселенной с положением, согласно которому математическое описание должно быть общим и простым. Скорее всего, с этим согласился бы и Пифагор. Интуитивно кажется, что и сама вселенная устроена в общих чертах просто, и более простые теории как бы ближе к реальности. Красота теории кажется близкой к простоте, и обе они как бы имеют больше бытия. В конце концов, «простыми» являются основные принципы симметрии и законы сохранения.
Однако не исключено, что слишком простым образом описать мироздание не получится.
Материя будет постоянно вносить помехи. Частично эти помехи тоже будут описываться математически, а именно в том случае, когда материя принимает в себя много структур разом. Но, скорее всего, мы будем сталкиваться с тем, что материя вносит просто белый шум, который отличается как раз отсутствием структуры, то есть является простым признаком бытия без всякого смысла.
Поэтому мне кажется, что помехи, вносимые материей, надо искать в каком-то другом месте. Этот вопрос пока остается открытым.