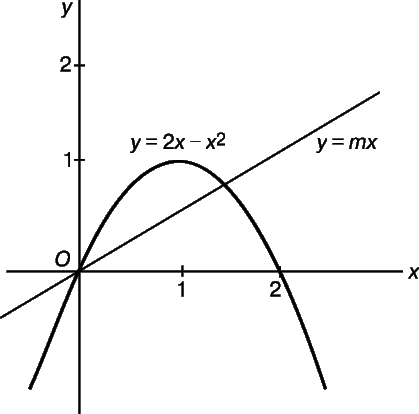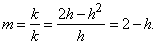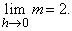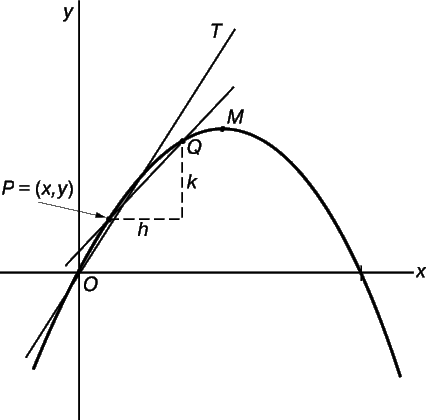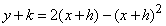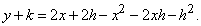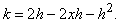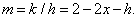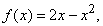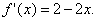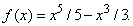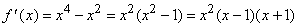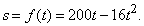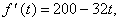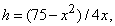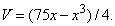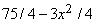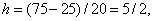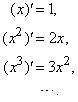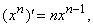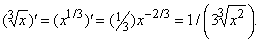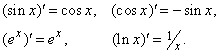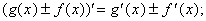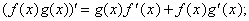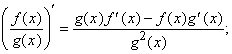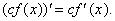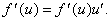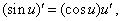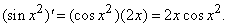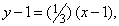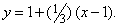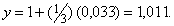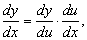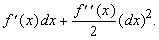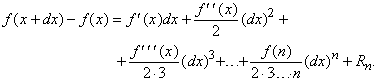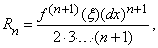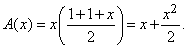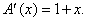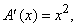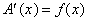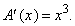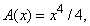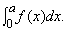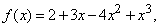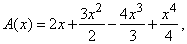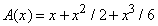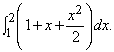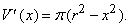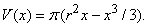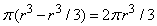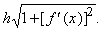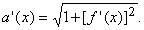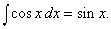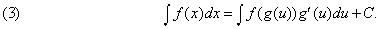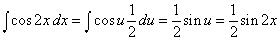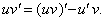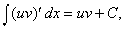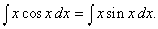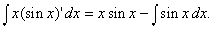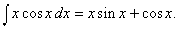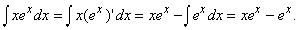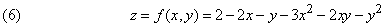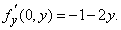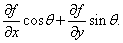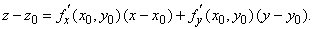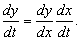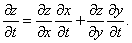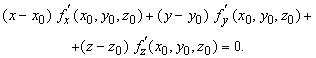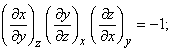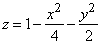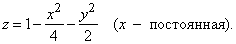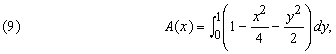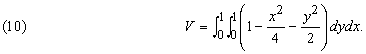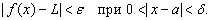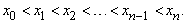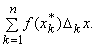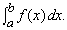Что такое матанализ в институте

Математический анализ

Математи́ческий ана́лиз — совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление.

В учебном процессе к анализу относят: [источник не указан 479 дней]

При этом элементы функционального анализа и теории интеграла Лебега даются факультативно, а ТФКП, вариационное исчисление, теория дифференциальных уравнений читаются отдельными курсами. Строгость изложения следует образцам конца XIX века и в частности использует наивную теорию множеств.

Содержание

История

Лейбниц и его ученики

Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается переменная величина, называется её дифференциалом… Для обозначения дифференциала переменной величины, которая сама выражается одной буквой, мы будем пользоваться знаком или символом . [5] … Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается дифференциал переменной величины, называется … вторым дифференциалом. [6]

Эти определения поясняются геометрически, при этом на рис. бесконечно малые приращения изображены конечными. Рассмотрение опирается на два требования (аксиомы). Первое:

Требуется, чтобы две величины, отличающиеся друг от друга лишь на бесконечно малую величину, можно было брать [при упрощении выражений?] безразлично одну вместо другой. [7]

Отсюда получается , далее

и проч. правила дифференцирования. Второе требование гласит:

Требуется, чтобы можно было рассматривать кривую линию как совокупность бесконечного множества бесконечно малых прямых линий. [8]

Продолжение каждой такой линии называется касательной к кривой. [9] Исследуя касательную, проходящую через точку , Лопиталь придаёт большое значение величине

,

достигающее экстремальных значений в точках перегиба кривой, отношению же к не придаётся никакого особого значения.

Примечательно нахождение точек экстремума. Если при непрерывном увеличении диаметра ордината сначала возрастает, а затем убывает, то дифференциал сначала положителен по сравнению с , а потом отрицателен.

Но всякая непрерывно возрастающая или убывающая величина не может превратиться из положительной в отрицательную, не проходя через бесконечность или нуль… Отсюда следует, что дифференциал наибольшей и наименьшей величины должен равняться нулю или бесконечности. [10]

Вероятно, эта формулировка не безупречна, если вспомнить о первом требовании: пусть, скажем, , тогда в силу первого требования

;

Далее, при помощи одних дифференциалов формулируются условия экстремума и рассмотрено большое число сложных задач, относящихся в основном к дифференциальной геометрии на плоскости. В конце книги, в гл. 10, изложено то, что теперь называют правилом Лопиталя, хотя и в не совсем обычной форме. Пусть величина ординаты кривой выражена дробью, числитель и знаменатель которой обращаются в нуль при . Тогда точка кривой с имеет ординату , равную отношению дифференциала числителя к дифференциалу знаменателя, взятому при .

Указывая на практическую полезность и простоту нового метода Лейбниц писал:

То, что человек, сведущий в этом исчислении, может получить прямо в трёх строках, другие учёнейшие мужи принуждены были искать, следуя сложными обходными путями.

Эйлер

Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этой переменного количества и чисел или постоянных количеств. [15]

Подчёркивая, что «основное различие функций лежит в способе составления их из переменного и постоянных», Эйлер перечисляет действия, «посредством которых количества могут друг с другом сочетаться и перемешиваться; действиями этими являются: сложение и вычитание, умножение и деление, возведение в степень и извлечение корней; сюда же следует отнести также решение [алгебраических] уравнений. Кроме этих действий, называемых алгебраическими, существует много других, трансцендентных, как-то: показательные, логарифмические и бесчисленные другие, доставляемые интегральным исчислением». [16] Такая трактовка позволяла без труда обращаться с многозначными функциями и не требовала пояснения, над каким полем рассматривается функция: выражение для счёта определено для комплексных значений переменных даже тогда, когда для рассматриваемой задачи это не нужно.

,

в котором лишь поздние авторы видели предельный переход. С аналитическими выражениями производились разнообразные преобразования, позволившие Эйлеру найти представления для элементарных функций в виде рядов, бесконечных произведений и т. д. Эйлер преобразует выражения для счёта так, как это делают в алгебре, не обращая внимания на возможность вычислить значение функции в точке по каждой из написанных формул.

Сам ход доказательства прекрасно демонстрирует технику использования бесконечно большого. Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее:

Полагая и , он получает

,

отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

.

Указав различные выражения для функций, которые теперь называют элементарными, Эйлер переходит к рассмотрению кривых на плоскости, начертанным свободным движением руки. По его мнению, не для всякой такой кривой можно отыскать единое аналитическое выражение (см. также Спор о струне). [19] В XIX веке с подачи Казорати [20] это утверждение считалось ошибочным: по теореме Вейерштрасса всякая непрерывная в современном смысле кривая может быть приближенно описана полиномами. На самом деле Эйлера это едва ли убедило, ведь нужно ещё переписать предельный переход при помощи символа .

Изложение дифференциального исчисления Эйлер начинает с теории конечных разностей, за ним в третьей главе следует философское разъяснение о том, что «бесконечно малое количество есть точно нуль», более всего не устроившее современников Эйлера. Затем из конечных разностей при бесконечно малом приращении образуются дифференциалы, а из интерполяционной формулу Ньютона — формула Тейлора. Этот метод в существенном восходит к работам Тейлора (1715 г.). При этом у Эйлера появляется устойчивое отношение , которое, однако, рассматривается как отношение двух бесконечно малых. Последние главы посвящены приближенному вычислению при помощи рядов.

В трёхтомном интегральном исчислении Эйлер трактует вводит понятие интеграла так:

Та функция, дифференциал которой , называется его интегралом и обозначается знаком , поставленным спереди. [21]

В целом же эта часть трактата Эйлера посвящена более общей с современной точки зрения задаче об интегрировании дифференциальных уравнений. При этом Эйлер находит ряд интегралов и дифференциальных уравнений, которые приводят к новым функциям, напр., -функции, эллиптические функции и т. д. Строгое доказательство их неэлементарности было дано в 1830-х годах Якоби для эллиптических функций и Лиувиллем (см. элементарные функции).

Лагранж

Следующим крупным произведением, сыгравшим значительную роль в развитии концепции анализа, явилась Теория аналитических функций [22] Лагранжа и обширный пересказ работ Лагранжа, выполненный Лакруа [23] в несколько эклектической манере.

Желая избавиться от бесконечно малого вовсе, Лагранж обратил связь между производными и рядом Тейлора. Под аналитической функцией Лагранж понимал произвольную функцию, исследуемую методами анализа. Саму функцию он обозначил как , дав графический способ записи зависимости — ранее же Эйлер обходился одними переменными. Для применения методов анализа по мнению Лагранжа необходимо, чтобы функция разлагалась в ряд

,

коэффициенты которого будут новыми функциями . Остаётся назвать производной (дифференциальным коэффициентом) и обозначить его как . Таким образом, понятие производной вводится на второй странице трактата и без помощи бесконечно малых. Остаётся заметить, что

,

поэтому коэффициент является удвоенной производной производной , то есть

и т. д. [24]

Такой подход к трактовке понятия производной используется в современной алгебре и послужил основой для создания теории аналитических функций Вейерштрасса.

Лагранж оперировал такими рядами как формальными и получил ряд замечательных теорем. В частности, впервые и вполне строго доказал разрешимость начальной задачи для обыкновенных дифференциальных уравнений в формальных степенных рядах. [25]

Вопрос об оценке точности приближений, доставляемых частными суммами ряда Тейлора, впервые был поставлен именно Лагранжем: в конце Теории аналитических функций он вывел то, что теперь называют формулой Тейлора с остаточным членом в форме Лагранжа. [26] Однако, в противоположность современным авторам, Лагранж не видел нужды в употреблении этого результата для обоснования сходимости ряда Тейлора.

Вопрос о том, действительно ли функции, употребимые в анализе, могут быть разложены в степенной ряд, впоследствии стал предметом дискуссии. Конечно, Лагранжу было известно, что в некоторых точках элементарные функции могут не разлагаться в степенной ряд, однако в этих точках они и недифференцируемы ни в каком смысле. Коши в своём Алгебраическом анализе привёл в качестве контрпримера функцию

доопределённую нулём в нуле. Эта функция всюду гладкая на вещественной оси и в нуле имеет нулевой ряд Маклорена, который, следовательно, не сходится к значению . Против этого примера Пуассон возразил, что Лагранж определял функцию как единое аналитическое выражение, в примере Коши же функция задана по разному в нуле, и при . Лишь в конце XIX века Прингсхейм [27] доказал, что существует бесконечно дифференцируемая функция, заданная единым выражением, ряд Маклорена для которой расходится. Пример такой функцией доставляет выражение

.

Дальнейшее развитие

В XVIII веке были разработаны и практически применены такие разделы анализа, как вариационное исчисление, обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных, преобразования Фурье и производящие функции. На фундаменте анализа возникла математическая физика, аналитические методы глубоко проникли в геометрию и даже в теорию чисел.

В XIX веке Коши первым дал анализу твёрдое логическое обоснование, введя понятие предела последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.

В последней трети XIX века Вейерштрасс произвёл арифметизацию анализа, полагая геометрическое обоснование недостаточным, и предложил классическое определение предела через ε-δ-язык. Он же создал первую строгую теорию множества вещественных чисел. В это же время попытки усовершенствования теоремы об интегрируемости по Риману привели к созданию классификации разрывности вещественных функций. Также были открыты «патологические» примеры (нигде не дифференцируемые непрерывные функции, заполняющие пространство кривые). В связи с этим Жордан разработал теорию меры, а Кантор — теорию множеств, и в начале XX века математический анализ был формализован с их помощью. Другим важным событием XX века стала разработка нестандартного анализа как альтернативного подхода к обоснованию анализа.

Источник

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

МАТЕМАТИЧЕСКИЙ АНАЛИЗ, раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и поверхностями (интегральное исчисление). Для задач математического анализа характерно, что их решение связано с понятием предела.

Начало математическому анализу положил в 1665 И.Ньютон и (около 1675) независимо от него Г.Лейбниц, хотя важную подготовительную работу провели И.Кеплер (1571–1630), Ф.Кавальери (1598–1647), П.Ферма (1601–1665), Дж.Валлис (1616–1703) и И.Барроу (1630–1677).

Чтобы сделать изложение более живым, мы будем прибегать к языку графиков. Поэтому читателю, возможно, будет полезно заглянуть в статью АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ, прежде чем приступать к чтению данной статьи.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Касательные.

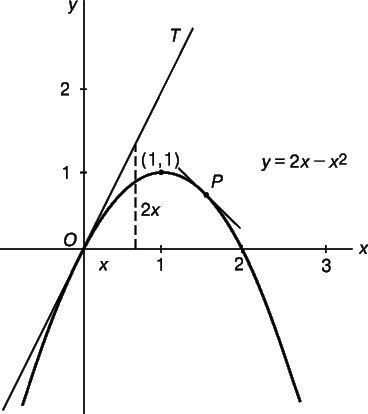
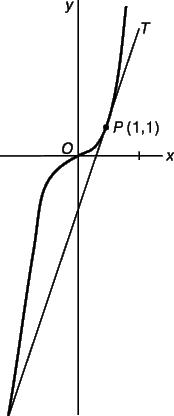
На рис. 1 касательная ОТ проведена через начало координат О = (0,0). Угловой коэффициент этой прямой равен 2, т.е. при изменении абсциссы на 1 ордината увеличивается на 2. Если x и y – координаты произвольной точки на ОТ, то, удаляясь от О на расстояние х единиц вправо, мы удаляемся от О на 2y единиц вверх. Следовательно, y/x = 2, или y = 2x. Это уравнение касательной ОТ к кривой y = 2x – x 2 в точке О.

Необходимо теперь объяснить, почему из множества прямых, проходящих через точку О, выбрана именно прямая ОТ. Чем же прямая с угловым коэффициентом 2 отличается от других прямых? Существует один простой ответ, и нам трудно удержаться от искушения привести его, используя аналогию с касательной к окружности: касательная ОТ имеет с кривой только одну общую точку, тогда как любая другая невертикальная прямая, проходящая через точку О, пересекает кривую дважды. В этом можно убедиться следующим образом.

Поскольку выражение y = 2x – x 2 можно получить вычитанием х 2 из y = 2x (уравнения прямой ОТ), то значения y для графика оказываются меньше знаний y для прямой во всех точках, за исключением точки x = 0. Следовательно, график всюду, кроме точки О, расположен ниже ОТ, и эта прямая и график имеют только одну общую точку. Кроме того, если y = mx – уравнение какой-нибудь другой прямой, проходящей через точку О, то обязательно найдутся две точки пересечения. Действительно, mx = 2x – x 2 не только при x = 0, но и при x = 2 – m. И только при m = 2 обе точки пересечения совпадают. На рис. 3 показан случай, когда m меньше 2, поэтому справа от О возникает вторая точка пересечения.

То, что ОТ – единственная невертикальная прямая, проходящая через точку О и имеющая с графиком лишь одну общую точку, не самое главное ее свойство. Действительно, если мы обратимся к другим графикам, то вскоре выяснится, что отмеченное нами свойство касательной в общем случае не выполняется. Например, из рис. 4 видно, что вблизи точки (1,1) график кривой y = x 3 хорошо аппроксимируется прямой РТ, имеющей однако, с ним более одной общей точки. Тем не менее, нам хотелось бы считать РТ касательной к этому графику в точке Р. Поэтому необходимо найти какой-то иной способ выделения касательной, чем тот, который так хорошо послужил нам в первом примере.

При очень малых h значение m близко к 2. Более того, выбирая h достаточно близким к 0, мы можем сделать m сколь угодно близким к 2. Можно сказать, что m «стремится к пределу», равному 2, когда h стремится к нулю, или что предел m равен 2 при h, стремящемся к нулю. Символически это записывается так:

Тогда касательная к графику в точке О определяется как прямая, проходящая через точку О, с угловым коэффициентом, равным этому пределу. Такое определение касательной применимо в общем случае.

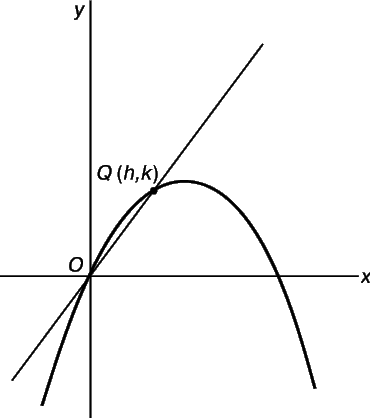
Покажем преимущества этого подхода еще на одном примере: найдем угловой коэффициент касательной к графику кривой y = 2x – x 2 в произвольной точке P = (x,y), не ограничиваясь простейшим случаем, когда P = (0,0).

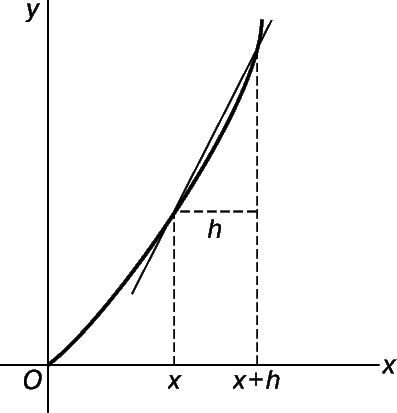
Пусть Q = (x + h, y + k) – вторая точка на графике, находящаяся на расстоянии h справа от Р (рис. 6). Требуется найти угловой коэффициент k/h секущей PQ. Точка Q находится на расстоянии

Раскрывая скобки, находим:

Следовательно, угловой коэффициент m секущей PQ равен

Теперь, когда h стремится к нулю, m стремится к 2 – 2x; последнюю величину мы и примем за угловой коэффициент касательной PT. (Тот же результат получится, если h принимает отрицательные значения, что соответствует выбору точки Q слева от P.) Заметим, что при x = 0 полученный результат совпадает с предыдущим.

то производную можно обозначить

Для того, чтобы узнать угловой коэффициент касательной к графику функции y = f(x) в какой-нибудь точке, необходимо подставить в f ў (x) соответствующее этой точке значение х. Таким образом, угловой коэффициент f ў (0) = 2 при х = 0, f ў (0) = 0 при х = 1 и f ў (2) = –2 при х = 2.

Тот факт, что кривая y = 2x – x 2 вблизи данной точки практически неотличима от ее касательной в этой точке, позволяет говорить об угловом коэффициенте касательной как об «угловом коэффициенте кривой» в точке касания. Такие образом, мы можем утверждать, что угловой коэффициент рассматриваемой нами кривой имеет в точке (0,0) угловой коэффициент 2. Можно также сказать, что при x = 0 скорость изменения y относительно x равна 2. В точке (2,0) угловой коэффициент касательной (и кривой) равен –2. (Знак минус означает, что при возрастании x переменная y убывает.) В точке (1,1) касательная горизонтальна. Мы говорим, что кривая y = 2x – x 2 имеет в этой точке стационарное значение.

Максимумы и минимумы.

Мы только что показали, что кривая f(x) = 2x – x 2 стационарна в точке (1,1). Так как f ў (x) = 2 – 2x = 2(1 – x), ясно, что при x, меньших 1, f ў (x) положительна, и, следовательно, y возрастает; при x, больших 1, f ў (x) отрицательна, и поэтому y убывает. Таким образом, в окрестности точки (1,1), обозначенной на рис. 6 буквой М, значение у растет до точки М, стационарно в точке М и убывает после точки М. Такая точка называется «максимумом», поскольку значение у в этой точке превосходит любые его значения в достаточно малой ее окрестности. Аналогично, «минимум» определяется как точка, в окрестности которой все значения y превосходят значение у в самой этой точке. Может также случиться, что хотя производная от f (x) в некоторой точке и обращается в нуль, ее знак в окрестности этой точки не меняется. Такая точка, не являющаяся ни максимумом, ни минимумом, называется точкой перегиба.

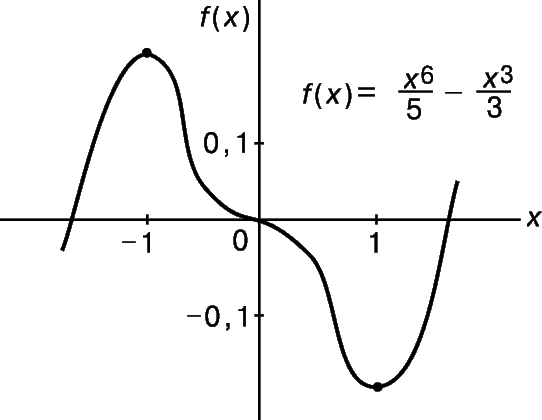
В качестве примера найдем стационарную точку кривой

Производная этой функции равна

и обращается в нуль при x = 0, х = 1 и х = –1; т.е. в точках (0,0), (1, –2/15) и (–1, 2/15). Если х чуть меньше –1, то f ў (x) отрицательна; если х чуть больше –1, то f ў (x) положительна. Следовательно, точка (–1, 2/15) – максимум. Аналогично, можно показать, что точка (1, –2/15) – минимум. Но производная f ў (x) отрицательна как до точки (0,0), так и после нее. Следовательно, (0,0) – точка перегиба.

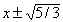
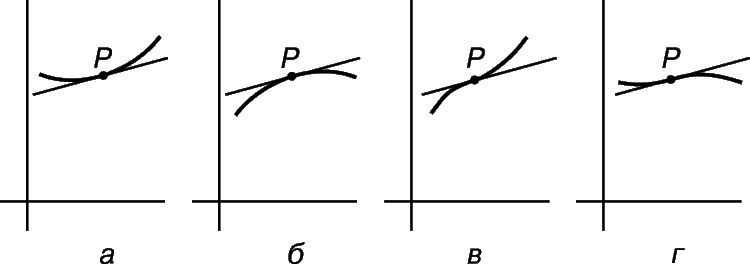
Проведенное исследование формы кривой, а также то обстоятельство, что кривая пересекает ось х при f(x) = 0 (т.е. при х = 0 или ) позволяют представить ее график примерно так, как показано на рис. 7.

В общем, если исключить необычные случаи (кривые, содержащие прямолинейные отрезки или бесконечное число изгибов), существуют четыре варианта взаимного расположения кривой и касательной в окрестности точки касания Р. (См. рис. 8, на котором касательная имеет положительный угловой коэффициент.)

1) По обе стороны от точки Р кривая лежит выше касательной (рис. 8,а). В этом случае говорят, что кривая в точке Р выпукла вниз или вогнута.

2) По обе стороны от точки Р кривая расположена ниже касательной (рис. 8,б). В этом случае говорят, что кривая выпукла вверх или просто выпукла.

3) и 4) Кривая располагается выше касательной по одну сторону от точки Р и ниже – по другую. В этом случае Р – точка перегиба.

Сравнивая значения f ў (x) по обе стороны от Р с ее значением в точке Р, можно определить, с каким из этих четырех случаев приходится иметь дело в конкретной задаче.

Приложения.

Все изложенное выше находит важные приложения в различных областях. Например, если тело брошено вертикально вверх с начальной скоростью 200 футов в секунду, то высота s, на которой они будут находиться через t секунд по сравнению с начальной точкой составит

Действуя так же, как в рассмотренных нами примерах, находим

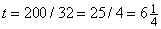
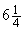
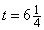
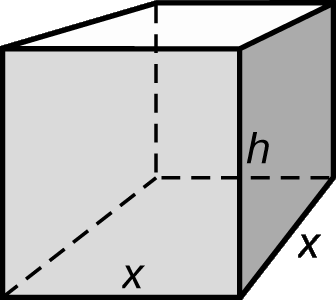
эта величина обращается в нуль при с. Производная f ў (x) положительна до значения с и отрицательна по истечении этого времени. Следовательно, s возрастает до , затем становится стационарной, а после убывает. Таково общее описание движения брошенного вверх тела. Из него мы узнаем, когда тело достигает высшей точки. Далее, подставляя t = 25/4 в f (t), мы получаем 625 футов, максимальную высоту подъема. В данной задаче f ў (t) имеет физический смысл. Эта производная показывает скорость, с которой тело движется в момент времени t.

Рассмотрим теперь приложение другого типа (рис. 9). Из листа картона площадью 75 см 2 требуется изготовить коробку с квадратным дном. Каковы должны быть размеры этой коробки, чтобы она имела максимальный объем? Если х – сторона основания коробки и h – ее высота, то объем коробки равен V = x 2 h, а площадь поверхности равна 75 = x 2 + 4xh. Преобразуя уравнение, получаем:

Производная от V оказывается равной

и обращается в нуль при х = 5. Тогда

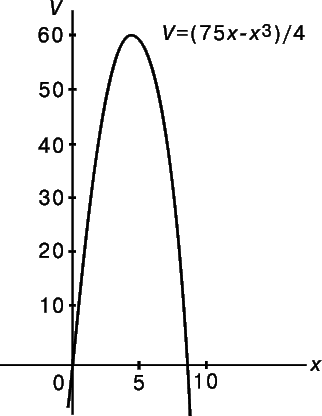
и V = 125/2. График функции V = (75x – x 3 )/4 показан на рис. 10 (отрицательные значения х опущены как не имеющие физического смысла в данной задаче).

Производные.

Важная задача дифференциального исчисления – создание методов, позволяющих быстро и удобно находить производные. Например, несложно посчитать, что

(Производная от постоянной, разумеется, равна нулю.) Нетрудно вывести общее правило:

где n – любое целое число или дробь. Например,

(На этом примере видно, как полезны дробные показатели степени.)

Приведем некоторые важнейшие формулы:

Существуют также следующие правила: 1) если каждая из двух функций g(x) и f(x) имеет производные, то производная их суммы равна сумме производных этих функций, а производная разности равна разности производных, т.е.

2) производная произведения двух функций вычисляется по формуле:

3) производная отношения двух функций имеет вид

4) производная функции, умноженной на константу, равна константе, умноженной на производную этой функции, т.е.

В нашем примере f(u) = sin u, f ў (u) = cos u, следовательно,

Эти и другие, аналогичные им, правила позволяют сразу же выписывать производные многих функций.

Линейные аппроксимации.

То обстоятельство, что, зная производную, мы можем во многих случаях заменить график функции вблизи некоторой точки ее касательной в этой точке, имеет огромное значение, поскольку с прямыми легче работать.

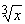
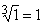
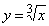
Эта идея находит непосредственное приложение в вычислении приближенных значений функций. Например, довольно трудно вычислить значение при x = 1,033. Но можно воспользоваться тем, что число 1,033 близко к 1 и что . Вблизи x = 1 мы можем заменить график кривой касательной, не совершая при этом сколько-нибудь серьезной ошибки. Угловой коэффициент такой касательной равен значению производной (x 1/3 ) ў = (1/3)x –2/3 при x = 1, т.е. 1/3. Так как точка (1,1) лежит на кривой и угловой коэффициент касательной к кривой в этой точке равен 1/3, уравнение касательной имеет вид

На этой прямой при х = 1,033

Полученное значение y должно быть очень близко к истинному значению y; и, действительно, оно лишь на 0,00012 больше истинного. В математическом анализе разработаны методы, позволяющие повышать точность такого рода линейных приближений. Эти методы обеспечивают надежность наших приближенных вычислений.

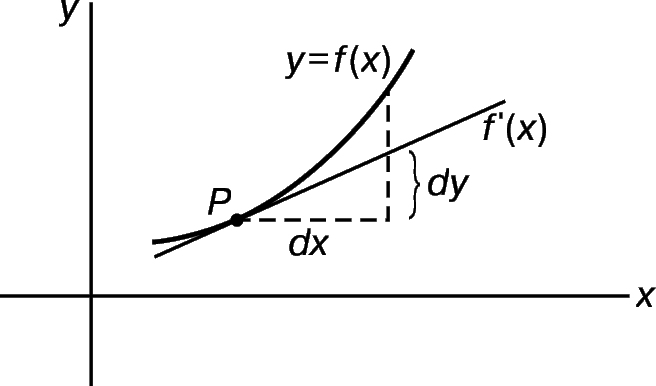
Только что описанная процедура наводит на мысль об одном полезном обозначении. Пусть P – точка, соответствующая на графике функции f переменной х, и пусть функция f(x) дифференцируема. Заменим график кривой вблизи точки Р касательной к нему, проведенной в этой точке. Если х изменить на величину h, то ордината касательной изменится на величину h Ч f ў (x). Если h очень мало, то последняя величина служит хорошим приближением к истинному изменению ординаты y графика. Если вместо h мы напишем символ dx (это не произведение!), а изменение ординаты y обозначим dy, то получим dy = f ў (x)dx, или dy/dx = f ў (x) (см. рис. 11). Поэтому вместо Dy или f ў (x) для обозначения производной часто используется символ dy/dx. Удобство этого обозначения зависит главным образом от явного появления цепного правила (дифференцирования сложной функции); в новых обозначениях эта формула выглядит следующим образом:

где подразумевается, что у зависит от u, а u в свою очередь зависит от х.

Величина dy называется дифференциалом у; в действительности она зависит от двух переменных, а именно: от х и приращения dx. Когда приращение dx очень мало, величина dy близка к соответствующему изменению величины y. Но предполагать, что приращение dx мало, нет необходимости.

Можно показать, что кривая в точке выпукла вниз, если вторая производная положительна, и выпукла вверх, если вторая производная отрицательна.

Если функция имеет вторую производную, то изменение величины y, соответствующее приращению dx переменной х, можно приближенно вычислить по формуле

Это приближение, как правило, лучше, чем то, которое дает дифференциал f ў (x)dx. Оно соответствует замене части кривой уже не прямой, а параболой.

Если у функции f(x) существуют производные более высоких порядков, то

Остаточный член имеет вид

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Площади.

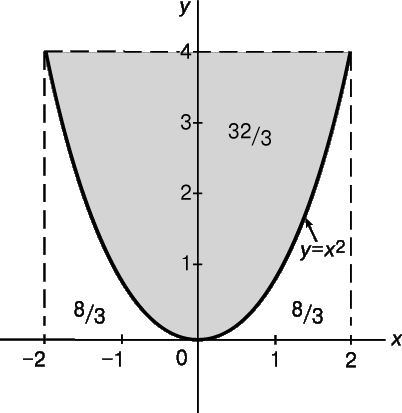
При изучении площадей криволинейных плоских фигур открываются новые аспекты математического анализа. Такого рода задачи пытались решать еще древние греки, для которых определение, например, площади круга было одной из труднейших задач. Больших успехов в решении этой проблемы добился Архимед, которому также удалось найти площадь параболического сегмента (рис. 12). С помощью весьма сложных рассуждений Архимед доказал, что площадь параболического сегмента составляет 2/3 от площади описанного прямоугольника и, следовательно, в данном случае равна (2/3)(16) = 32/3. Как мы увидим в дальнейшем, этот результат можно легко получить методами математического анализа.

Предшественники Ньютона и Лейбница, главным образом Кеплер и Кавальери, решали задачи о вычислении площадей криволинейных фигур с помощью метода, который трудно назвать логически обоснованным, но который оказался чрезвычайно плодотворным. Когда же Валлис в 1655 соединил методы Кеплера и Кавальери с методами Декарта (аналитической геометрией) и воспользовался только что зародившейся алгеброй, сцена для появления Ньютона была полностью подготовлена.

Основная теорема.

Великое открытие Ньютона и Лейбница позволило исключить трудоемкий процесс перехода к пределу суммы площадей. Это было сделано благодаря новому взгляду на понятие площади. Суть в том, что мы должны представить площадь под кривой как порожденную ординатой, движущейся слева направо и спросить, с какой скоростью изменяется заметаемая ординатами площадь. Ключ к ответу на этот вопрос мы получим, если рассмотрим два частных случая, в которых площадь заранее известна.

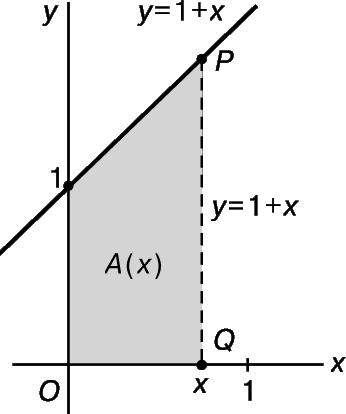
Начнем с площади под графиком линейной функции y = 1 + x, поскольку в этом случае площадь можно вычислить с помощью элементарной геометрии.

Пусть A(x) – часть плоскости, заключенная между прямой y = 1 + x и отрезком OQ (рис. 14). При движении QP вправо площадь A(x) возрастает. С какой скоростью? Ответить на этот вопрос нетрудно, так как мы знаем, что площадь трапеции равна произведению ее высоты на полусумму оснований. Следовательно,

Скорость изменения площади A(x) определяется ее производной

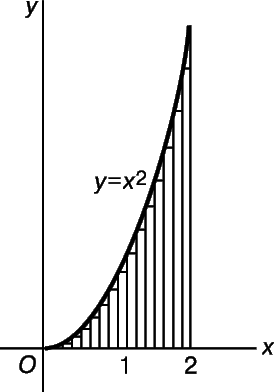
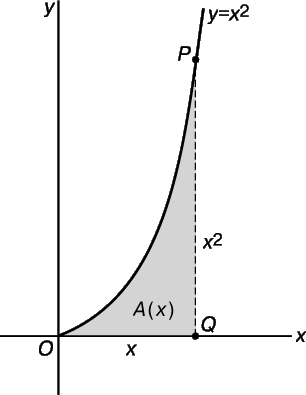
Мы видим, что A ў (x) совпадает с ординатой у точки Р. Случайно ли это? Попробуем проверить на параболе, изображенной на рис. 15. Площадь A (x) под параболой у = х 2 в интервале от 0 до х равна A(x) = ( 1 /₃)(x)(x 2 ) = x 3 /3. Скорость изменения этой площади определяется выражением

которое в точности совпадает с ординатой у движущейся точки Р.

Если предположить, что это правило выполняется в общем случае так, что

есть скорость изменения площади под графиком функции y = f(x), то этим можно воспользоваться для вычислений и других площадей. На самом деле, соотношение A ў (x) = f(x) выражает фундаментальную теорему, которую можно было бы сформулировать следующим образом: производная, или скорость изменения площади как функции от х, равна значению функции f (x) в точке х.

Например, чтобы найти площадь под графиком функции y = x 3 от 0 до х (рис. 16), положим

Возможный ответ гласит:

В математическом анализе доказывается, что другого ответа, кроме приведенного выше выражения для A(x), не существует. Покажем, что это утверждение правдоподобно с помощью следующего эвристического (нестрогого) рассуждения. Предположим, что существует какое-либо второе решение В(x). Если A(x) и В(x) «стартуют» одновременно с нулевого значения при х = 0 и все время изменяются с одинаковой скоростью, то их значения ни при каком х не могут стать различными. Они должны всюду совпадать; следовательно, существует единственное решение.

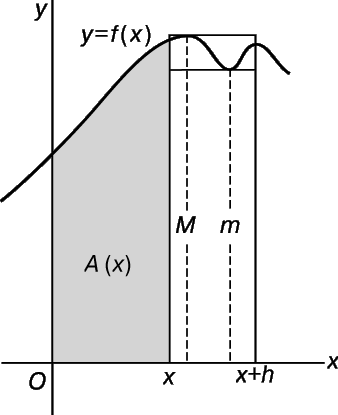
Как можно обосновать соотношение A ў (x) = f(x) в общем случае? На этот вопрос можно ответить, лишь изучая скорость изменения площади как функции от х в общем случае. Пусть m – наименьшее значение функции f (x) в интервале от х до (x + h), а M – наибольшее значение этой функции в том же интервале. Тогда приращение площади при переходе от х к (x + h) должно быть заключено между площадями двух прямоугольников (рис. 17). Основания обоих прямоугольников равны h. Меньший прямоугольник имеет высоту m и площадь mh, больший, соответственно, М и Mh. На графике зависимости площади от х (рис. 18) видно, что при изменении абсциссы на h, значение ординаты (т.е. площадь) увеличивается на величину, заключенную между mh и Mh. Угловой коэффициент секущей на этом графике находится между m и M. Что происходит, когда h стремится к нулю? Если график функции y = f(x) непрерывен (т.е. не содержит разрывов), то и М, и m стремятся к f(x). Следовательно, угловой коэффициент A ў (x) графика площади как функции от х равен f(x). Именно к такому заключению и требовалось придти.

Лейбниц предложил для площади под кривой y = f(x) от 0 до а обозначение

При строгом подходе этот так называемый определенный интеграл должен быть определен как предел некоторых сумм на манер Валлиса. Учитывая полученный выше результат, ясно, что этот интеграл вычисляется при условии, что мы можем найти такую функцию A(x), которая обращается в нуль при х = 0 и имеет производную A ў (x), равную f (x). Нахождение такой функции принято называть интегрированием, хотя уместнее эту операцию было бы называть антидифференцированием, имея в виду, что она является в некотором смысле обратной дифференцированию. В случае многочлена интегрирование выполняется просто. Например, если

в чем нетрудно убедиться, продифференцировав A(x).

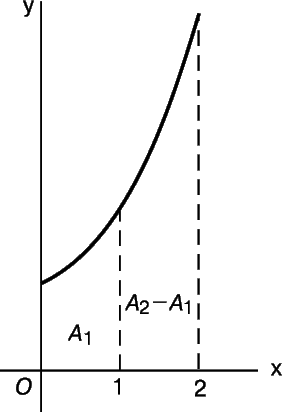
Чтобы вычислить площадь А₁ под кривой y = 1 + x + x 2 /2, заключенную между ординатами 0 и 1, мы просто записываем

и, подставляя х = 1, получаем A₁ = 1 + 1 /₂ + 1 /₆ = 5 /₃. Площадь A(x) от 0 до 2 равна A₂ = 2 + 4 /₂ + 8 /₆ = 16 /₃. Как видно из рис. 19, площадь, заключенная между ординатами 1 и 2, равна A₂ – A₁ = 11 /₃. Обычно она записывается в виде определенного интеграла

Объемы.

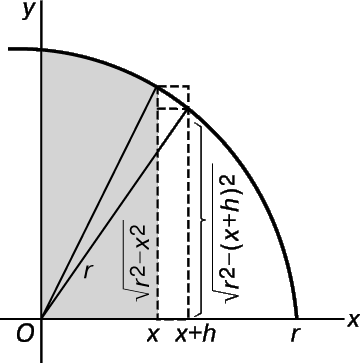
Аналогичные рассуждения позволяют удивительно просто вычислять объемы тел вращения. Продемонстрируем это на примере вычисления объема шара, еще одной классической задачи, которую древним грекам, с помощью известных им методов, удалось решить с великим трудом.

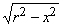
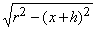
Повернем часть плоскости, заключенной внутри четверти круга радиуса r, на угол 360 ° вокруг оси х. В результате мы получим полушарие (рис. 20), объем которого обозначим V(x). Требуется определить, с какой скоростью возрастает V(x) с увеличением x. Переходя от х к х + h, нетрудно убедиться в том, что приращение объема меньше, чем объем p (r 2 – x 2 )h кругового цилиндра радиуса и высотой h, и больше, чем объем p [r 2 – (x + h) 2 ]h цилиндра радиуса и высотой h. Следовательно, на графике функции V(x) угловой коэффициент секущей заключен между p (r 2 – x 2 ) и p [r 2 – (x + h) 2 ]. Когда h стремится к нулю, угловой коэффициент стремится к

При x = r мы получаем

для объема полушария, и, следовательно, 4 p r 3 /3 для объема всего шара.

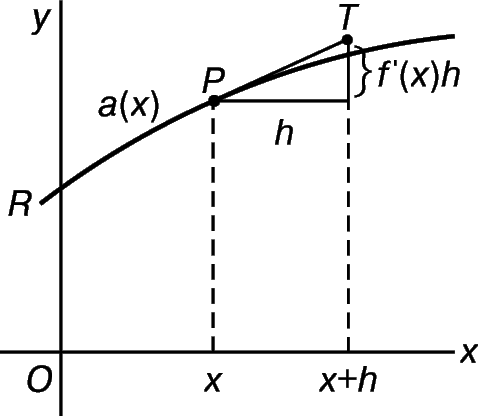
Аналогичный метод позволяет находить длины кривых и площади искривленных поверхностей. Например, если a(x) – длина дуги PR на рис. 21, то наша задача состоит в вычислении a ў( x). Воспользуемся на эвристическом уровне приемом, который позволяет не прибегать к обычному предельному переходу, необходимому при строгом доказательстве результата. Предположим, что скорость изменения функции а(x) в точке Р такая же, какой она была бы при замене кривой ее касательной PT в точке P. Но из рис. 21 непосредственно видно, при шаге h вправо или влево от точки х вдоль РТ значение а(x) меняется на

Следовательно, скорость изменения функции a(x) составляет

Чтобы найти саму функцию a(x), необходимо лишь проинтегрировать выражение, стоящее в правой части равенства. Оказывается, что для большинства функций выполнить интегрирование довольно трудно. Поэтому разработка методов интегрального исчисления составляет большую часть математического анализа.

Первообразные.

Произвольную первообразную функцию для заданной функции f(x) принято называть неопределенным интегралом от f(x) и обозначать его в виде

Например, так как (sin x) ў = cos x, справедлива формула

Во многих случаях, когда существует формула для неопределенного интеграла от заданной функции, ее можно найти в многочисленных широко публикуемых таблицах неопределенных интегралов. Табличными являются интегралы от элементарных функций (в их число входят степени, логарифмы, показательная функция, тригонометрические функции, обратные тригонометрические функции, а также их конечные комбинации, получаемые с помощью операций сложения, вычитания, умножения и деления). С помощью табличных интегралов можно вычислить интегралы и от более сложных функций. Существует много способов вычисления неопределенных интегралов; наиболее распространенный из них метод подстановки или замены переменной. Он состоит в том, что если мы хотим в неопределенном интеграле (2) заменить x на некоторую дифференцируемую функцию x = g(u), то, чтобы интеграл не изменился, надо x заменить на g ў (u)du. Иначе говоря, справедливо равенство

Приведем еще один метод интегрирования – метод интегрирования по частям. Он основан на известной уже формуле

Ее можно записать так:

Проинтегрировав левую и правую части, и учитывая, что

Эта формула называется формулой интегрирования по частям.

Из (5), полагая u = x и v = sin x, получаем

А поскольку (–cos x) ў = sin x мы находим, что 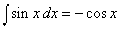и

Следует подчеркнуть, что мы ограничились лишь весьма кратким введением в весьма обширный предмет, в котором накоплены многочисленные остроумные приемы.

Функции двух переменных.

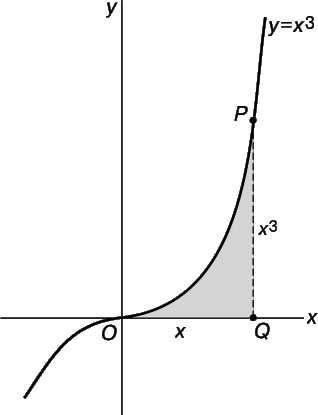
В связи с кривой y = f(x) мы рассмотрели две задачи.

1) Найти угловой коэффициент касательной к кривой в данной точке. Эта задача решается вычислением значения производной f ў (x) в указанной точке.

2) Найти площадь под кривой над отрезком оси х, ограниченную вертикальными линиями х = а и х = b. Эта задача решается вычислением определенного интеграла .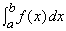

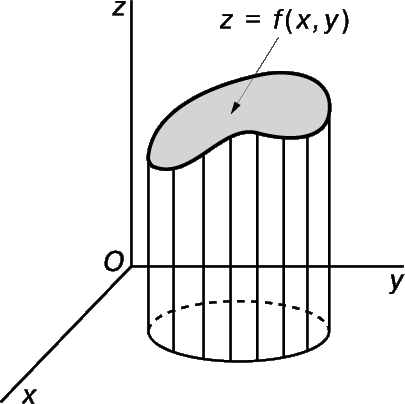
Каждая из этих задач имеет аналог в случае поверхности z = f(x,y).

1) Найти касательную плоскость к поверхности в данной точке.

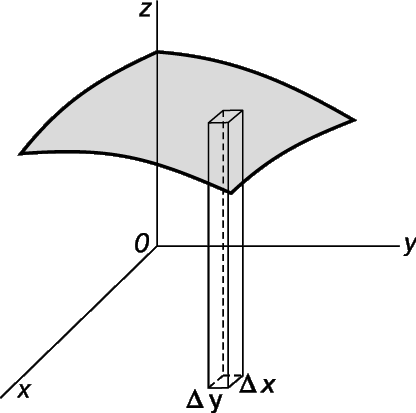
2) Найти объем под поверхностью над частью плоскости ху, ограниченной кривой С, а сбоку – перпендикулярами к плоскости xy, проходящими через точки граничной кривой С (см. рис. 22).

Следующие примеры показывают, как решаются эти задачи.

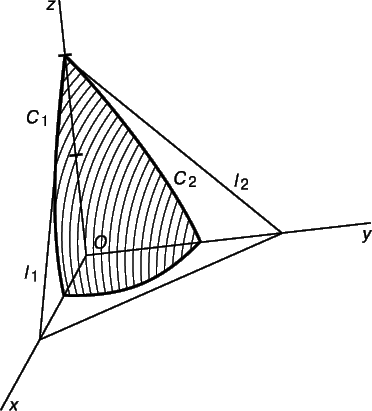
Пример 4. Найти касательную плоскость к поверхности

Плоскость определена, если заданы две лежащие в ней пересекающиеся прямые. Одну из таких прямых (l₁) мы получим в плоскости xz (у = 0), вторую (l₂) – в плоскости yz (x = 0) (см. рис. 23).

Так как f ў y(0,0) = –1, кривая С₂ – линия пересечения поверхности с плоскостью yz – имеет касательную l₂, задаваемую уравнениями z = 2 – y, х = 0. Искомая касательная плоскость содержит обе прямые l₁ и l₂ и записывается уравнением

Это – уравнение плоскости. Кроме того, мы получаем прямые l₁ и l₂, полагая, соответственно, у = 0 и х = 0.

В том, что уравнение (7) действительно задает касательную плоскость, на эвристическом уровне можно убедиться, если заметить, что это уравнение содержит члены первого порядка, входящие в уравнение (6), и что члены второго порядка можно представить в виде –[2x 2 + (x + y) 2 ]. Так как это выражение отрицательно при всех значениях х и у, кроме х = у = 0, поверхность (6) всюду лежит ниже плоскости (7), кроме точки Р = (0,0,0). Можно сказать, что поверхность (6) выпукла вверх в точке Р.

Пример 5. Найти касательную плоскость к поверхности z = f(x,y) = x 2 – y 2 в начале координат 0.

Однако в окрестности начала координат наша поверхность не находится по одну сторону от касательной плоскости. Действительно, кривая С₁ всюду, за исключением точки 0, лежит выше касательной плоскости, а кривая С₂ – соответственно ниже ее. Поверхность пересекает касательную плоскость z = 0 по прямым у = х и у = –х. Про такую поверхность говорят, что она имеет седловую точку в начале координат (рис. 24).

Частные производные.

В предыдущих примерах мы использовали производные от f (x,y) по х и по у. Рассмотрим теперь такие производные в более общем плане. Если у нас имеется функция двух переменных, например, F(x,y) = x 2 – xy, то мы можем определить в каждой точке две ее «частные производные», одну – дифференцируя функцию по х и фиксируя у, другую – дифференцируя по у и фиксируя х. Первая из этих производных обозначается как f ў x(x,y) или ¶ f/ ¶ x; вторая – как f ў y(x,y) или ¶ f/ ¶ y. Если f(x,y) = x 2 – xy, то ¶ f/ ¶ x = 2x – y и ¶ f/ ¶ y = –x. Заметим, что частные производные от любой функции – это, вообще говоря, новые функции. На практике эти функции в свою очередь дифференцируемы. 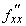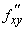Частные производные от f ў x по х и у принято обозначать, соответственно, и или ¶ 2f/ ¶ x 2 и ¶ 2f/ ¶ x ¶ y; аналогичные обозначения используются и для частных производных от f ў y. Если обе смешанные производные (по х и у, по у и х) непрерывны, то ¶ 2f/ ¶ x ¶ y = ¶ 2f/ ¶ y ¶ x; в нашем примере ¶ 2f/ ¶ x ¶ y = ¶ 2f/ ¶ y ¶ x = –1.

Частная производная f ў x(x,y) указывает скорость изменения функции f в точке (x,y) в направлении возрастания х, а f ў y(x,y) – скорость изменения функции f в направлении возрастания у. Скорость изменения функции f в точке (х,у) в направлении прямой, составляющей угол q с положительным направлением оси х, называется производной от функции f по направлению; ее величина представляет собой комбинацию двух частных производных от функции f – по х и по у, и равна

Как мы уже видели в частных случаях, касательная плоскость к поверхности z = f(x,y) в точке (x₀, y₀) имеет уравнение

Если обозначить x – x₀ через dx, а y – y₀ через dy, то уравнение касательной плоскости означает, что изменение dz = z – z₀ в касательной плоскости, когда x изменяется на dx, а у – на dy, равно dz = f ў x(x₀,y₀)dx + f ў y(x₀,y₀)dy. Эта величина называется дифференциалом функции f. Если f имеет непрерывные частные производные, то изменение dz в касательной плоскости почти равно (при малых dx и dy) истинному изменению z на поверхности, но вычислить дифференциал обычно бывает легче.

Уже рассмотренная нами формула из метода замены переменной, известная как производная сложной функции или цепное правило, в одномерном случае, когда у зависит от х, а х зависит от t, имеет вид:

Для функций двух переменных аналогичная формула имеет вид:

Понятия и обозначения частного дифференцирования нетрудно обобщить на более высокие размерности. В частности, в случае если поверхность задана неявно уравнением f(x,y,z) = 0, уравнению касательной плоскости к поверхности можно придать более симметричную форму: уравнение касательной плоскости в точке (x₀,y₀,z₀) имеет вид

Если задана поверхность f(x,y,z) = 0 и мы хотим узнать, что происходит на поверхности, то обычно любые две из трех переменных можно считать независимыми, а третью переменную рассматривать как зависимую от них. Иногда для обозначения частных производных в этом случае используется символ ( ¶ z/ ¶ x)_y, чтобы подчеркнуть, что дифференцирование производится по х, а у считается независимой переменной. Имеем:

эта формула подчеркивает, что мы не можем придать независимый смысл символам ¶ x, ¶ y, ¶ z или рассматривать ¶ z/ ¶ x как отношение ¶ z к ¶ x.

Обратимся теперь к примеру второй задачи, т.е. вычислению объемов.

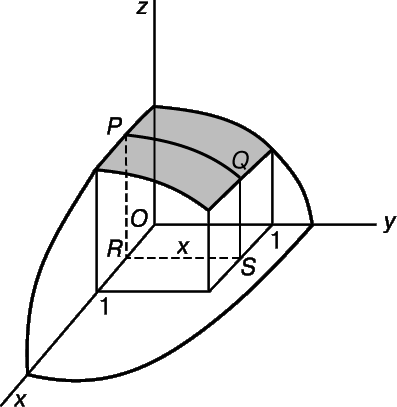
Пример 6. Найти объем тела, заключенного между поверхностью

и над единичным квадратом, см. на рис. 25.

Пусть V(x) – объем, ограниченный поверхностью и пятью плоскостями, а именно z = 0, y = 0, y = 1, x = 0 и плоскостью PQRS, перпендикулярной оси х и пересекающей эту ось на расстоянии х от начала координат.

Нетрудно видеть, что производная V ў (x) равна А(x), площади поперечного сечения PQRS. Таким образом,

Но А(x) – площадь под кривой

где интегрирование проводится по у, а х рассматривается как постоянная. Подставляя (9) в (8), запишем V в виде повторного интеграла

В формуле (10) предполагается, что сначала проводится внутреннее интегрирование. Результат этого интегрирования, выражение [( 5 /₆) – (x 2 /4)], затем интегрируется по х от 0 до 1. Окончательный результат равен 3/4.

Формулу (10) можно интерпретировать и как так называемый двойной интеграл, т.е. как предел суммы объемов элементарных «клеток». Каждая такая клетка имеет основание D x D y и высоту, равную высоте поверхности над некоторой точкой прямоугольного основания (см. рис. 26). Можно показать, что обе точки зрения на формулу (10) эквивалентны. Двойные интегралы используются для нахождения центров тяжести и многочисленных моментов, встречающихся в механике.

Более строгое обоснование математического аппарата.

До сих пор мы излагали понятия и методы математического анализа на интуитивном уровне и, не колеблясь, прибегали к геометрическим фигурам. Нам осталось кратко рассмотреть более строгие методы, появившиеся в 19 и 20-м столетиях.

В начале 19 в., когда эпоха штурма и натиска в «создании математического анализа» завершилась, на первый план вышли вопросы его обоснования. В работах Абеля, Коши и ряда других выдающихся математиков были точно определены понятия «предела», «непрерывной функции», «сходящегося ряда». Это было необходимо для того, чтобы внести логический порядок в основание математического анализа с тем, чтобы сделать его надежным инструментом исследования. Потребность в тщательном обосновании стала еще более очевидной после открытия в 1872 Вейерштрассом всюду непрерывных, но нигде не дифференцируемых функций (график таких функций в каждой своей точке имеет излом). Этот результат произвел ошеломляющее впечатление на математиков, поскольку явно противоречил их геометрической интуиции. Еще более поразительным примером ненадежности геометрической интуиции стала построенная Д.Пеано непрерывная кривая, целиком заполняющая некоторый квадрат, т.е. проходящая через все его точки. Эти и другие открытия вызвали к жизни программу «арифметизации» математики, т.е. придания ей большей надежности путем обоснования всех математических понятий с помощью понятия числа. Почти пуританское воздержание от наглядности в работах по основаниям математики имело свое историческое оправдание.

По современным канонам логической строгости недопустимо говорить о площади под кривой y = f(x) и над отрезком оси х, даже если f – непрерывная функция, не определив предварительно точный смысл термина «площадь» и не установив, что определенная таким образом площадь действительно существует. Эта задача была успешно решена в 1854 Б.Риманом, который дал точное определение понятия определенного интеграла. С тех пор идея суммирования, стоящая за понятием определенного интеграла, была предметом многих глубоких исследований и обобщений. В результате сегодня удается придать смысл определенному интегралу, даже если подынтегральная функция является повсюду разрывной. Новые понятия интегрирования, в создание которых большой вклад внес А.Лебег (1875–1941) и другие математики, приумножили мощь и красоту современного математического анализа.

Вряд ли было бы уместно входить в детали всех этих и других понятий. Ограничимся лишь тем, что приведем строгие определения предела и определенного интеграла.

(Вертикальные черточки означают, что мы имеем дело с абсолютной величиной заключенного между ними числа.)

Такая процедура называется разбиением интервала [a, b]. Пусть x_k * – любое число из замкнутого интервала [x_k – 1, x_k], k = 1, 2. n, и пусть D kx = x_k – x_k – 1 – длина этого интервала. Просуммируем все произведения f(x_k * ) D kx (k = 1, 2. n) и обозначим полученную сумму

Если эта сумма имеет предел L, когда n стремится к бесконечности и наибольшая длина D kx стремится к нулю, причем L не зависит от выбора x_k * и x_k, то L называется определенным интегралом от f(x) по [a, b] в смысле Римана и обозначается

В заключение скажем, что математический анализ, являясь крайне ценным инструментом в руках ученого и инженера, и сегодня привлекает внимание математиков как источник плодотворных идей. В то же время современное развитие как будто свидетельствует и о том, что математический анализ все более поглощается такими доминирующими в 20 в. разделами математики, как абстрактная алгебра и топология. См. также ФУНКЦИЙ ТЕОРИЯ; ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, тт. 1–2. М., 1970
Никольский С.М. Курс математического анализа, тт. 1–2. М., 1983

Источник