Что такое матан в школе

Матан – что это такое и где его начало?

Большинство последних моих постов рассмотрены по таком разделе математики, как математический анализ. Многие первокурсники считают этот предмет самым сложным, хотя и есть другие, которые намного сложнее, но изучаются на старших курсах. Даже после окончания университета в большинства, одни из воспоминаний – это недосыпанные ночи через матан. И решил будет не лишним рассказать немного о его сути и истории.

Математическим анализом называют систему дисциплин, которые объединены следующими характеристиками. Эти дисциплины, в основном, изучают количественные соотношения действительного мира (в отличие от геометрических дисциплин, занимающихся его пространственными свойствами). Здесь есть небольшое сходство с арифметикой, так как сами соотношения выражаются с помощью числовых величин. Но в арифметике (и в алгебре) рассматриваются преимущественно постоянные величины (которые характеризуют состояния), а в математическом анализе переменные величины, характеризуют сами процессы. Основные понятия анализа – это функция и предел, с помощью разных их свойств и происходит дальнейшее изучение.

Многие разделы математического анализа сейчас существуют, как отдельные предметы, ну например, дифференциальные уравнения, функциональный анализ. Сейчас основными разделами анализа будут: дифференциальное исчисление, интегральное исчисление и теория рядов.

Зачатки методов математического анализа были использованы ещё древнегреческим математиком Архимедом. Но уже в XVII веке эти методы были систематизированы и получили новый толчок к развитию. А на рубеже XVII и XVIII веков великий английский математик и физик И. Ньютон и знаменитый немецкий философ и математик Г. В. Лейбниц, завершили создание основных разделов математического анализа: дифференциального и интегрального исчисления, а также положили основу учения о рядах и о дифференциальных уравнениях. В XVIII веке Л. Эйлер, который сделал очень много для развития математики и работал в нескольких государствах, разработал последние два раздела и заложил основу других дисциплин математического анализа.

И так к концу XVIII века накопился огромный фактический материал, но он был недостаточно разработан в логическом отношении. Этот недостаток был устранен усилиями крупнейших ученых XIX века, таких, как О. Л. Коши] во Франции, Н. И. Лобачевский в России, Н. X. Абель в Норвегии, Г. Ф. Б. Риман в Германии и др. Которые довели не одну теорему, что сейчас часто используется при обучении математического анализа.

Источник

Математический анализ

Математи́ческий ана́лиз — совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление.

В учебном процессе к анализу относят: [источник не указан 479 дней]

При этом элементы функционального анализа и теории интеграла Лебега даются факультативно, а ТФКП, вариационное исчисление, теория дифференциальных уравнений читаются отдельными курсами. Строгость изложения следует образцам конца XIX века и в частности использует наивную теорию множеств.

Содержание

История

Лейбниц и его ученики

Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается переменная величина, называется её дифференциалом… Для обозначения дифференциала переменной величины, которая сама выражается одной буквой, мы будем пользоваться знаком или символом . [5] … Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается дифференциал переменной величины, называется … вторым дифференциалом. [6]

Эти определения поясняются геометрически, при этом на рис. бесконечно малые приращения изображены конечными. Рассмотрение опирается на два требования (аксиомы). Первое:

Требуется, чтобы две величины, отличающиеся друг от друга лишь на бесконечно малую величину, можно было брать [при упрощении выражений?] безразлично одну вместо другой. [7]

Отсюда получается , далее

и проч. правила дифференцирования. Второе требование гласит:

Требуется, чтобы можно было рассматривать кривую линию как совокупность бесконечного множества бесконечно малых прямых линий. [8]

Продолжение каждой такой линии называется касательной к кривой. [9] Исследуя касательную, проходящую через точку , Лопиталь придаёт большое значение величине

,

достигающее экстремальных значений в точках перегиба кривой, отношению же к не придаётся никакого особого значения.

Примечательно нахождение точек экстремума. Если при непрерывном увеличении диаметра ордината сначала возрастает, а затем убывает, то дифференциал сначала положителен по сравнению с , а потом отрицателен.

Но всякая непрерывно возрастающая или убывающая величина не может превратиться из положительной в отрицательную, не проходя через бесконечность или нуль… Отсюда следует, что дифференциал наибольшей и наименьшей величины должен равняться нулю или бесконечности. [10]

Вероятно, эта формулировка не безупречна, если вспомнить о первом требовании: пусть, скажем, , тогда в силу первого требования

;

Далее, при помощи одних дифференциалов формулируются условия экстремума и рассмотрено большое число сложных задач, относящихся в основном к дифференциальной геометрии на плоскости. В конце книги, в гл. 10, изложено то, что теперь называют правилом Лопиталя, хотя и в не совсем обычной форме. Пусть величина ординаты кривой выражена дробью, числитель и знаменатель которой обращаются в нуль при . Тогда точка кривой с имеет ординату , равную отношению дифференциала числителя к дифференциалу знаменателя, взятому при .

Указывая на практическую полезность и простоту нового метода Лейбниц писал:

То, что человек, сведущий в этом исчислении, может получить прямо в трёх строках, другие учёнейшие мужи принуждены были искать, следуя сложными обходными путями.

Эйлер

Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этой переменного количества и чисел или постоянных количеств. [15]

Подчёркивая, что «основное различие функций лежит в способе составления их из переменного и постоянных», Эйлер перечисляет действия, «посредством которых количества могут друг с другом сочетаться и перемешиваться; действиями этими являются: сложение и вычитание, умножение и деление, возведение в степень и извлечение корней; сюда же следует отнести также решение [алгебраических] уравнений. Кроме этих действий, называемых алгебраическими, существует много других, трансцендентных, как-то: показательные, логарифмические и бесчисленные другие, доставляемые интегральным исчислением». [16] Такая трактовка позволяла без труда обращаться с многозначными функциями и не требовала пояснения, над каким полем рассматривается функция: выражение для счёта определено для комплексных значений переменных даже тогда, когда для рассматриваемой задачи это не нужно.

,

в котором лишь поздние авторы видели предельный переход. С аналитическими выражениями производились разнообразные преобразования, позволившие Эйлеру найти представления для элементарных функций в виде рядов, бесконечных произведений и т. д. Эйлер преобразует выражения для счёта так, как это делают в алгебре, не обращая внимания на возможность вычислить значение функции в точке по каждой из написанных формул.

Сам ход доказательства прекрасно демонстрирует технику использования бесконечно большого. Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее:

Полагая и , он получает

,

отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

.

Указав различные выражения для функций, которые теперь называют элементарными, Эйлер переходит к рассмотрению кривых на плоскости, начертанным свободным движением руки. По его мнению, не для всякой такой кривой можно отыскать единое аналитическое выражение (см. также Спор о струне). [19] В XIX веке с подачи Казорати [20] это утверждение считалось ошибочным: по теореме Вейерштрасса всякая непрерывная в современном смысле кривая может быть приближенно описана полиномами. На самом деле Эйлера это едва ли убедило, ведь нужно ещё переписать предельный переход при помощи символа .

Изложение дифференциального исчисления Эйлер начинает с теории конечных разностей, за ним в третьей главе следует философское разъяснение о том, что «бесконечно малое количество есть точно нуль», более всего не устроившее современников Эйлера. Затем из конечных разностей при бесконечно малом приращении образуются дифференциалы, а из интерполяционной формулу Ньютона — формула Тейлора. Этот метод в существенном восходит к работам Тейлора (1715 г.). При этом у Эйлера появляется устойчивое отношение , которое, однако, рассматривается как отношение двух бесконечно малых. Последние главы посвящены приближенному вычислению при помощи рядов.

В трёхтомном интегральном исчислении Эйлер трактует вводит понятие интеграла так:

Та функция, дифференциал которой , называется его интегралом и обозначается знаком , поставленным спереди. [21]

В целом же эта часть трактата Эйлера посвящена более общей с современной точки зрения задаче об интегрировании дифференциальных уравнений. При этом Эйлер находит ряд интегралов и дифференциальных уравнений, которые приводят к новым функциям, напр., -функции, эллиптические функции и т. д. Строгое доказательство их неэлементарности было дано в 1830-х годах Якоби для эллиптических функций и Лиувиллем (см. элементарные функции).

Лагранж

Следующим крупным произведением, сыгравшим значительную роль в развитии концепции анализа, явилась Теория аналитических функций [22] Лагранжа и обширный пересказ работ Лагранжа, выполненный Лакруа [23] в несколько эклектической манере.

Желая избавиться от бесконечно малого вовсе, Лагранж обратил связь между производными и рядом Тейлора. Под аналитической функцией Лагранж понимал произвольную функцию, исследуемую методами анализа. Саму функцию он обозначил как , дав графический способ записи зависимости — ранее же Эйлер обходился одними переменными. Для применения методов анализа по мнению Лагранжа необходимо, чтобы функция разлагалась в ряд

,

коэффициенты которого будут новыми функциями . Остаётся назвать производной (дифференциальным коэффициентом) и обозначить его как . Таким образом, понятие производной вводится на второй странице трактата и без помощи бесконечно малых. Остаётся заметить, что

,

поэтому коэффициент является удвоенной производной производной , то есть

и т. д. [24]

Такой подход к трактовке понятия производной используется в современной алгебре и послужил основой для создания теории аналитических функций Вейерштрасса.

Лагранж оперировал такими рядами как формальными и получил ряд замечательных теорем. В частности, впервые и вполне строго доказал разрешимость начальной задачи для обыкновенных дифференциальных уравнений в формальных степенных рядах. [25]

Вопрос об оценке точности приближений, доставляемых частными суммами ряда Тейлора, впервые был поставлен именно Лагранжем: в конце Теории аналитических функций он вывел то, что теперь называют формулой Тейлора с остаточным членом в форме Лагранжа. [26] Однако, в противоположность современным авторам, Лагранж не видел нужды в употреблении этого результата для обоснования сходимости ряда Тейлора.

Вопрос о том, действительно ли функции, употребимые в анализе, могут быть разложены в степенной ряд, впоследствии стал предметом дискуссии. Конечно, Лагранжу было известно, что в некоторых точках элементарные функции могут не разлагаться в степенной ряд, однако в этих точках они и недифференцируемы ни в каком смысле. Коши в своём Алгебраическом анализе привёл в качестве контрпримера функцию

доопределённую нулём в нуле. Эта функция всюду гладкая на вещественной оси и в нуле имеет нулевой ряд Маклорена, который, следовательно, не сходится к значению . Против этого примера Пуассон возразил, что Лагранж определял функцию как единое аналитическое выражение, в примере Коши же функция задана по разному в нуле, и при . Лишь в конце XIX века Прингсхейм [27] доказал, что существует бесконечно дифференцируемая функция, заданная единым выражением, ряд Маклорена для которой расходится. Пример такой функцией доставляет выражение

.

Дальнейшее развитие

В XVIII веке были разработаны и практически применены такие разделы анализа, как вариационное исчисление, обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных, преобразования Фурье и производящие функции. На фундаменте анализа возникла математическая физика, аналитические методы глубоко проникли в геометрию и даже в теорию чисел.

В XIX веке Коши первым дал анализу твёрдое логическое обоснование, введя понятие предела последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.

В последней трети XIX века Вейерштрасс произвёл арифметизацию анализа, полагая геометрическое обоснование недостаточным, и предложил классическое определение предела через ε-δ-язык. Он же создал первую строгую теорию множества вещественных чисел. В это же время попытки усовершенствования теоремы об интегрируемости по Риману привели к созданию классификации разрывности вещественных функций. Также были открыты «патологические» примеры (нигде не дифференцируемые непрерывные функции, заполняющие пространство кривые). В связи с этим Жордан разработал теорию меры, а Кантор — теорию множеств, и в начале XX века математический анализ был формализован с их помощью. Другим важным событием XX века стала разработка нестандартного анализа как альтернативного подхода к обоснованию анализа.

Источник

Что такое матан в школе

Автор оригинала: Kalid Azad, перевёл: Филипп Сорокин.

Это третий перевод из серии статей на тему математического анализа, хотя по хронологии статья является первой. В дальнейшем переводы статей будут идти в соответствии с оригинальной хронологией, с пропуском уже переведённых.

Статья рассчитана на студентов и всех интересующихся высшей математикой, и представляет из себя введение в математический анализ с рассуждениями и интересными примерами его применения. Подойдёт и для чайников.

Введение

Мои отношения с математическим анализом строятся на любви и ненависти: этот предмет демонстрирует красоту математики и агонию математического образования.

Математический анализ связывает темы в элегантной, ломающей мозг манере. Моя ближайшая аналогия – теория эволюции Дарвина: однажды поняв, вы начинаете видеть природу с точки зрения выживания. Вы начинаете понимать, почему употребление лекарств приводит к появлению микробов, устойчивых к ним (выживание сильнейших). Вы понимаете, почему сахар и жир настолько вкусны (вкус, как поощрение за потребление высококалорийных продуктов в период дефицита). Всё начинает сходиться.

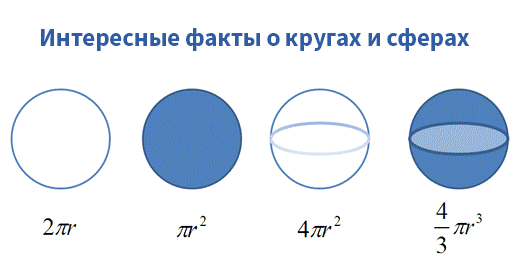
Математический анализ даёт такое же прозрение. Не кажется ли вам, что эти формулы каким-то образом связаны между собой?

Да, они связаны. Но большинство из нас изучает эти формулы по отдельности. Математический анализ помогает нам разобраться с каждой, начиная с длины окружности, равной 2πr – греки оценили бы это.

К сожалению, математический анализ может стать олицетворением того, что с математическим образованием что-то не так. Большинство уроков строятся на надуманных примерах, скрытых доказательствах и запоминании, что отбивает нашу интуицию и энтузиазм.

Так не должно быть.

Математика, искусство и идеи

Я кое-чему научился в школе: в математике самое трудное – не математика, а мотивация. В частности, мотивация оставаться воодушевлённым несмотря на:

– Преподавателей, которых больше заботит издание своих научных трудов, чем преподавание.

– Бытующие мнения, что математика – это сложно, скучно, непопулярно или «не ваш предмет».

– Учебники и программы обучения, которые больше заточены на получение прибыли и результатов тестирования, чем на понимание предмета.

«Плач математика» [pdf] является отличным эссе по этому вопросу, вызвавшим общественный резонанс (здесь было 3 ссылки, 2 из которых оказались битые – прим. пер.):

«…если бы мне пришлось разрабатывать механизм, предназначенный специально для разрушения естественного любопытства и любви к построению закономерностей у детей, я бы никогда не справился с этой работой так же хорошо, как это делается сейчас – у меня бы просто не хватило воображения, чтобы придумать настолько бессмысленные, душераздирающие идеи, которые составляют современное математическое образование.»

Представьте себе такое изучение искусства: Дети, никакого рисования руками в детском саду. Вместо этого, давайте-ка изучим химию красок, физику света и анатомию глаза. По прошествии 12 лет эти дети (которые уже подростки), если ещё не ненавидят искусство, смогут начать рисовать самостоятельно. В конце концов, у них есть «строгие, проверяемые» основы для того, чтобы начать ценить искусство. Правильно?

С поэзией также. Представьте себе процесс изучения этой цитаты (формулировки):

«Но главное – будь верен самому себе, и, следственно, как дважды два – четыре, ни перед кем не будешь ты фальшив.» – Вильям Шекспир, Гамлет

Математика и поэзия – это пальцы, указывающие на Луну. Не путайте палец с Луной. Формулы – это средство достижения цели, способ выразить математическую истину.

Мы забываем, что математика – это идеи, а не рутинные манипуляции с формулами, которые их выражают.

Ладно, приятель, в чём твоя отличная идея?

Дерзкие, да? Ну, чего я точно не буду делать, так это воссоздавать учебники по подобию уже существующих. Если вам прямо сейчас нужны ответы для какого-то серьёзного экзамена, то есть множество веб-сайтов, видеозаписей уроков и 20-минутных спринтов, чтобы помочь вам (оригинальные ссылки на англоязычные ресурсы – прим. пер.).

Вместо этого, давайте обсудим основные идеи математического анализа. Уравнений недостаточно – я хочу делиться «ага!»-моментами, от которых что-то щёлкает внутри.

Формальный математический язык – это лишь один из способов общения. Диаграммы, анимации и просто разговоры зачастую могут дать больше понимания, чем страница книги, полная доказательств.

Но мат. анализ – это сложно!

Я думаю, что любой сможет понять основные идеи математического анализа. Нам не нужно быть писателями, чтобы наслаждаться Шекспиром.

Это в пределах вашей досягаемости, если вы знаете алгебру и имеете простой интерес к математике. Не так давно чтение и письмо были работой опытных писцов. Но сегодня с этим может справиться и 10-летний ребёнок. Почему?

Потому что мы этого ожидаем. Ожидания играют огромную роль в том, что нам кажется возможным. Поэтому ожидайте, что мат. анализ – это просто ещё один предмет. Для немногих из нас это становится повседневной работой (писатели, математики). Но остальные всё ещё могут восхищаться тем, что происходит, и расширять свой кругозор.

Дело в том, как далеко ты намерен зайти. Я бы хотел, чтобы все смогли понять основные идеи математического анализа и сказали «вау».

Так о чём же мат. анализ?

Некоторые называют математический анализ «отраслью математики, которая занимается нахождением пределов, дифференцированием и интегрированием функций одной или нескольких переменных». Это правильно, но не несёт пользы для начинающих.

Вот моё мнение: мат. анализ делает с алгеброй то, что алгебра сделала с арифметикой.

– Арифметика – это манипулирование числами (сложение, умножение и т.д.).

– Алгебра находит закономерности между числами: a 2 + b 2 = c 2 – известное соотношение, описывающее стороны прямоугольного треугольника. Алгебра находит целые множества чисел – если вы знаете a и b, то вы можете найти c.

– Математический анализ находит закономерности между уравнениями: обратите внимание, как одно уравнение (длина окружности = 2πr) походит на другое (площадь окружности = πr 2 ).

При использовании мат. анализа у нас появляются новые вопросы:

– Как уравнение растёт и сжимается? Накапливается ли со временем?

– Когда оно достигает своего самого высокого/низкого значения?

– Как мы используем переменные, которые постоянно меняются? (тепло, движение, популяция, …).

– И множество других вопросов!

Алгебра и математический анализ – это дуэт для решения проблем: мат. анализ находит новые уравнения, а алгебра решает их. Как и эволюция, мат. анализ расширяет ваше понимание того, как работает природа.

Пример, пожалуйста

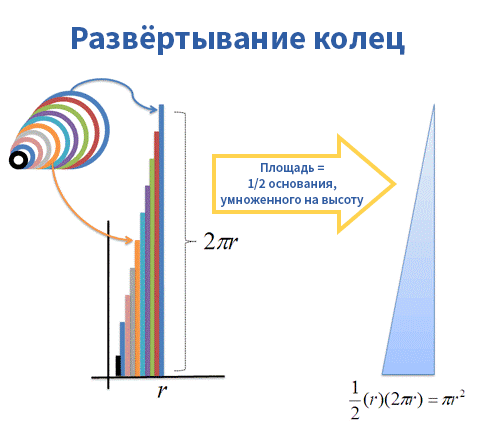
Давайте пройдёмся. Предположим, мы знаем уравнение для нахождения длины окружности (2πr) и хотим найти площадь круга. Что делать?

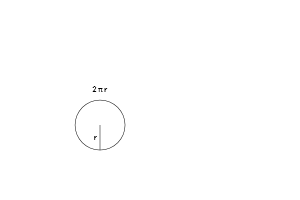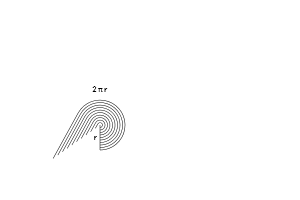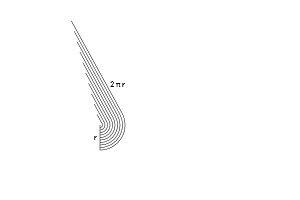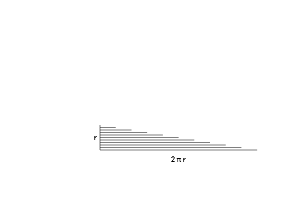
Представьте окружность в виде диска, который, как матрёшка, заполнен кольцами, идущими от краёв к центру.

Есть два способа изобразить диск:

– Нарисовать круг и закрасить его.

– Нарисовать множество колец толстым маркером.

Количество «пространства» (площади) должно быть одинаковым в обоих случаях, верно? Но как много пространства занимает одно кольцо?

Ну, самое большое кольцо имеет радиус «r» и длину окружности «2π», умноженную на текущий радиус. А последнее кольцо (самое маленькое – прим. пер.) больше похоже на точку без окружности.

Теперь всё выглядит совершенно необычно. Давайте развернём эти кольца и выстроим каждое из них в линию. Что произойдёт?

– Мы получим кучу линий, образующих неровный треугольник. Но чем тоньше и чаще будут расположены кольца, тем менее зубчатым будет треугольник (подробнее об этом в будущих статьях).

– С одной стороны будет наименьшее кольцо (0), а с другой наибольшее (2πr).

– У нас есть кольца, идущие от радиуса, равного 0, до равного «r». Для каждого возможного радиуса (от 0 до r) мы просто вставляем развёрнутое кольцо в соответствующее место.

Вау! Площадь всех колец = Площадь треугольника = Площадь круга!

Это был быстрый пример, но вы ведь уловили основную мысль? Мы взяли диск, разделили его и сложили сегменты по-другому. Математический анализ показал нам, что диск и кольцо тесно связаны: диск на самом деле просто куча колец.

Это частая тема мат. анализа: Большие штуки складываются из маленьких частей. И иногда с маленькими частями проще работать.

Примечание о примерах

Многие примеры из математического анализа основаны на физике. Это здорово, но это же может быть трудно для понимания: ответьте честно, как часто вы вспоминаете уравнение для нахождения скорости объекта? Реже, чем раз в неделю.

Я предпочитаю начинать с физических, визуальных примеров, потому что так работает наш ум. Например, можем ли мы сделать такое же кольцо/круг, как в примере выше? Вы можете собрать такой круг из нескольких трубоочистителей, разделить на кольца и выпрямить их в грубый треугольник, чтобы проверить, действительно ли математика работает. С уравнением для вычисления скорости так не прокатит.

Примечание о соответствии канонам (для математических гиков)

Я чувствую, как математические педанты заводят свои клавиатуры. Несколько слов о «строгости».

Знаете ли вы, что мы изучаем не тот же самый мат. анализ, каким он был во времена открытия Ньютоном и Лейбницем? Они использовали интуитивные идеи «флюксий» и «бесконечных чисел», которые в последствии были вытеснены пределами, так как «Конечно, это работает на практике. Но работает ли это в теории?».

Мы создаём сложные механические конструкции, чтобы «в соответствии с канонами» доказывать математический анализ, но мы потеряли нашу интуитивное понимание в процессе.

Мы смотрим на сладость сахара, как на химическую реакцию в мозге вместо того, чтобы признать его способом природы сказать: «В этом много энергии. Ешь это.»

Я не хочу (и не могу) преподавать курсы анализа или обучать исследователей. Разве было бы плохо, если бы все понимали мат. анализ на «нестрогом» уровне, таким, каким его сделал Ньютон? Изменило ли бы это их взгляд на мир, как изменило у Ньютона?

Преждевременное внимание к «канонам» отталкивает студентов и затрудняет изучение математики. Пример: e технически определяется пределом, но интуитивное понимание экспоненциального роста в том, как он был открыт. Натуральный логарифм можно рассматривать, как интеграл, или как время, необходимое для роста. Какое из объяснений лучше подойдёт начинающим? (перевод двух статей из этого абзаца будет позже – прим. пер.)

Давайте немного порисуем руками и по ходу этого займёмся химией. Счастливой математики!

Начнем с поражения множества реформ математического образования. Уже долгие годы все большее внимание уделяется разладу в системе математического образования. Оплачиваются исследования, собираются конференции, формируются бессчетные комитеты учителей, авторов и издателей учебников, чтобы «исправить ситуацию». Не упустив ни капли собственной издательской выгоды (на любые флуктуации политики обучения они отвечают предложением новых редакций своих нечитабельных уродищ), все эти реформаторы упустили главное: математическая программа должна быть не исправлена — она должна быть выброшена вон.

Вся эта болтовня и показуха касательно того, какие «пункты программы» и в каком порядке следует учить, использовать эту нотацию вместо той нотации, какой модели калькулятор, Господи прости, нужен школьнику, — все это напоминает перестановку стульев на палубе тонущего «Титаника». Математика есть музыка разума. Заниматься математикой — значит совершать открытия и строить предположения; жить вдохновением и интуицией; значит оказываться в отчаянии — не потому, что предмет не имеет смысла, а потому, что вы придали ему смысл и все еще не понимаете, как ведет себя ваше создание; значит испытать и прорыв фонтана идей, и поражение художника; и в ужасе неметь от почти что физически невыносимого, переполняющего вас чувства прекрасного; да значит быть живым, черт побери! Уберите это из математики, и можете собирать сколько угодно умных конференций, и это ничего не изменит. Оперируйте, сколько хотите, дорогие доктора: пациент уже мертв.

Наипечальнейшая часть этих реформ — попытки «сделать математику интересной» и «важной в жизни детей». Вам не надо делать математику интересной — она уже более интересна, чем вы сможете вынести! И торжество ее в неважности для жизни — вот почему она так занимательна.

Попытки изобразить математику полезной и нужной для ежедневных дел всегда натужны и убоги: «Видите, дети, как просто, когда знаешь алгебру, высчитать, сколько Марии лет, если ей на два года больше, чем дважды ее возраст семь лет назад!» — как будто кто-то в жизни получит эту безумную информацию вместо настоящего возраста. Алгебра — не инструмент для жизни, это искусство симметрии и чисел, и потому достойно постижения само по себе.

Даны сумма и разность двух чисел. Каковы сами числа?

Вот простой, элегантный вопрос, и не надо лезть из кожи вон, чтобы придать ему привлекательности. Древние вавилоняне любили решать такие задачи, и наши ученики их тоже любят. (Да и вам, надеюсь, понравится!) Нам не надо заворачиваться в тройные узлы, чтобы придать математике важность для ежедневных дел. Ее важность, как и важность искусства вообще — в осмыслении человеческого опыта.

Или, может быть, вы думаете, что дети хотят чего-то, относящегося к их ежедневным делам? Может быть, их восхищает что-то практическое, например, сложный процент по кредиту? Людей восхищает фантазия, и это именно то, что математика может дать — убежище от ежедневного, волшебный бальзам от практических забот.

Другая проблема — когда авторы учебников начинают «сюсюкать», чтобы сделать математику «дружественной» и победить «страх перед математикой» (одна из множества болезней, на самом деле вызываемых школой). Чтобы ученики могли запомнить формулы, вы можете придумать целую историю о том, как Иван Демьянович едет на машине вокруг Елизаветы Макаровны и говорит ей, как хороши были ее два пирога (L=2πR), или что ее пироги квадратные (S=πR²), или еще какую-нибудь глупость. А как же настоящий рассказ о проблеме измерения кривых, о Евдоксе 11 и Архимеде и методе неделимых, о трансцендентности числа π? Что интереснее — измерять приблизительный размер кружка по клеточкам, а потом вычислять длину окружности по формуле, которую вам дали без объяснения, или услышать историю одной из самых прекрасных, захватывающих задач, и самых ярких и сильных идей всей человеческой истории? Мы убиваем в детях интерес к кругам, в конце концов!

Почему мы не даем ученикам услышать об этом, не то чтобы дать им возможность самим позаниматься математикой, прийти к собственным идеям и мнениям? Какой еще предмет изучают, даже не упоминая его истории, философии, основоположения, эстетических критериев и текущего положения вещей? Какой еще предмет отбрасывает первоисточники — чудесных произведений искусства, выполненных самыми творческими умами истории — в пользу убогих третьесортных учебников?

Главная проблема школьной математики в том, что в ней нет задач. Да, я знаю, что выдается за задачи на уроках: эти безвкусные, скучные упражнения. «Вот задача. Вот как ее решить. Да, такие бывают на экзамене. На дом задачи 1—15». Что за тоскливый способ изучать математику: стать дрессированным шимпанзе.

Но задача — настоящий, честный до мозга костей естественный человеческий вопрос — это нечто другое. Какова длина диагонали куба? Закончатся ли простые числа? Бесконечность — число или нет? Сколькими способами можно симметрично покрыть поверхность плитками? История математики — это история решения этих вопросов, не бессмысленного пережевывания формул и алгоритмов, вместе с натянутыми упражнениями, чтобы их применять.

Хорошая задача — такая, решения которой вы не знаете. Вот где загадка, вот что дает настоящие возможности! Хорошая задача не стоит в отдельности, но служит стартовой площадкой для других интересных задач. Треугольник занимает половину описанного прямоугольника. А как насчет пирамиды в кубе? Можно ли эту задачу решить тем же способом?

Я принимаю идею обучения школьников технике решения, и я сам это делаю. Но это не цель. Техника в математике, как и в любом искусстве, должна изучаться в контексте. Великие задачи, их история, творческий процесс — вот этот контекст. Дайте ученикам хорошую задачу, пусть они поломают головы, пусть у них не получится ее решить. Посмотрите, что у них выйдет. Дождитесь до того момента, когда они страстно захотят свежую идею. Тогда научите их какой-то технике, только немного.

Отложите в сторону планы уроков и диапроекторы, мерзкие красочные учебники, компакт-диски и весь остальной парад уродов бродячего цирка, и займитесь с учениками математикой! Учителя живописи не тратят время на чтение учебников и зазубривание техники — они просто дают детям рисовать. Они ходят от мольберта к мольберту и подсказывают, направляют:

— Я думала о задаче с треугольником, и кое-что заметила. Смотрите, если треугольник наклонный, то он не занимает половины прямоугольника!

— Превосходное наблюдение! Наше рассуждение с рассечением треугольника было в предположении, что вершина находится над основанием. Теперь нам нужна новая идея.

— Попытаться рассечь его как-то иначе?

— Конечно. Перепробуй всевозможные идеи. Дай мне знать, что у тебя выйдет!

Как же нам учить детей математике? Выбирая занимательные и естественные задачи, в соответствии с их вкусами, интересами и опытом. Давая им время делать открытия и строить гипотезы. Помогая им выстраивать доказательства и создавая атмосферу здорового и живого математического критицизма. Улавливая, куда меняется их интерес. В общем, выстраивая честные и открытые интеллектуальные отношения с учениками. Это требует слишком большой ответственности и слишком большой открытости — короче, это слишком много работы!

Гораздо проще быть пассивным передатчиком готовых школьных «материалов» и следовать инструкции, как на бутылке шампуня — «лекция, экзамен, повторить» — чем глубоко мыслить о собственном предмете и передавать этот смысл честно и наилучшим образом своим ученикам. Нас просто уговаривают забросить сложную задачу принятия решений своим умом и совестью, и вместо этого «проходить программу». Это попросту путь наименьшего сопротивления:

Авторы учебников имеют такое же отношение к учителям, как:
а) фармацевтические компании к докторам;
б) компании звукозаписи к диск-жокеям;
в) корпорации к депутатам;
г) все вышеперечисленное.

Труд математики, как и живописи и поэзии, состоит в тяжелой творческой работе. Поэтому математику очень сложно преподавать. Математика — медленный созерцательный процесс. Изготовить произведение искусства занимает время, а, чтобы распознать его, нужен искусный учитель. Разумеется, легче вывесить список правил, чем вести за собой будущих художников, как легче написать инструкцию к телевизору, чем книгу с изложением своей точки зрения.

Математика — искусство, а искусство должно преподаваться действующими мастерами или по крайней мере педагогами, любящими искусство и способными его распознать. Не обязательно учиться музыке у профессионального композитора, но отдадите ли вы ребенка в обучение кому-то, кто не умеет играть сам и не слышал ни одного музыкального произведения за всю жизнь? Возьмете ли вы учителем рисования того, кто не держал в руке карандаша и никогда не был в музее? Как же тогда мы допускаем в учителя математики того, кто не создал ни одного математического произведения, не знает ни истории, ни философии предмета, ни последних достижений математики, ничего, в конце концов, из того, что он должен преподавать своим несчастным ученикам? Что же это за учитель? Как они могут учить то, чего сами не знают? Я не умею танцевать, но мне и в голову не придет, будто я могу вести танцевальный класс (хоть я мог бы и попробовать, но это выглядело бы ужасно). Разница в том, что я знаю, что я не умею танцевать. Мне никто не скажет, что я хорошо танцую, даже если я знаю кучу танцевальных терминов.

Я не пытаюсь даже сказать, что учителя математики должны быть профессиональными математиками — нет, я и не подхожу к этому. Но не должны ли они хотя бы понимать, что такое математика, знать ее, и любить?

Если учеба превращается в простую передачу информации, если в ней нет делимого с учеником восхищения и чуда, если учителя суть пассивные получатели информации, а не творцы новых идей — есть ли тогда надежда у наших школьников? Если сложение дробей для учителя является случайным набором правил, а не результатом творчества или результатом эстетически обоснованного выбора, тогда несомненно надежды у бедных учеников и быть не может.

В частности, вы не можете учить учить. Педагогические курсы — полная бессмыслица. Да, вы можете пройти курсы по раннему детскому развитию и еще чему-нибудь, обучиться «использовать доску эффективно», готовить организованный «план урока» (что, кстати, обеспечивает вашему уроку плановость, следовательно, лживость), но вы никогда не станете учителем, если не будете настоящим человеком. Преподавание — это открытость и честность, желание делиться радостью знания, любовь к учению. Без этого все педагогические дипломы мира не помогут вам — они совершенно бесполезны.

Это так просто. Ученики не пришельцы с Альфы Центавра. Они понимают прекрасное, они видят узор, они от природы любопытны, как и все мы. Просто расскажите им! И — еще важнее — слушайте их!

Симплицио. Ну ладно, мне ясно, что в математике есть элемент искусства и что мы могли бы лучше это объяснять. Но ведь это, наверное, слишком заумная штука, чтобы ожидать ее от школы? Мы же не философов там учим, нам же надо, чтобы они арифметику знали до той степени, чтобы нормально вписаться в общество.

Сальвиати. Это не так! Школьная математика занимается множеством вещей, не связанных с возможностью вписаться в общество — например, алгеброй и тригонометрией. Эти дисциплины совершенно бесполезны для ежедневных дел. Я просто предлагаю вот что: раз мы включаем эти вещи в план среднего образования, так уж делать это органично и естественно. К тому же, как я уже говорил, то, что из предмета можно получить практическую пользу, еще не говорит о том, чтобы на этой пользе обучение фокусировать. Конечно, следует научиться читать, чтобы заполнить бланк на почте, но ведь мы не для этого детей учим чтению. Мы учим их чтению для высшей цели — дать им доступ к прекрасным и значительным идеям. Не только было бы бесполезно учить третьеклассников писать, давая им заполнять бланки налоговых деклараций — это бы и не работало! Мы учимся, потому что нам интересно то, чему мы учимся, здесь и сейчас, не потому, что это будет полезно в дальнейшем. А ведь с математикой мы именно так и поступаем.

Симплицио. Но разве третьеклассники не должны знать арифметики?

Сальвиати. Зачем? Ты хочешь научить их складывать 427 и 389? Это не из тех вопросов, что спрашивают восьмилетки. Да не все взрослые полностью понимают десятичную позиционную арифметику, а ты хочешь, чтобы у третьеклассников была полная ясность? Или тебе все равно, поймут они это или нет? Слишком рано это для такого механического обучения. Конечно, их можно научить, но, думаю, от этого вреда выйдет больше, чем пользы. Лучше дождаться, пока у них не появится естественный интерес к числам.

Симплицио. Так чем же дети должны заниматься на уроках математики?

Симплицио. Похоже, мы возьмем этим на себя слишком большой риск. Что же, нам не учить школьников арифметике — ведь они не будут уметь складывать и вычитать!

Сальвиати. Полагаю, что мы куда больше рискуем создать школу, лишенную творческого выражения, где функции ученика будут запоминать даты, формулы и списки слов, а затем выплевывать их на стандартных экзаменах, готовясь стать «строителем светлого будущего».

Симплицио. Но послушай, ведь должен быть какой-то минимум математических фактов, которые должен знать любой образованный человек!

Симплицио. Но у нас нет столько времени, чтобы каждый ученик изобрел себе математику! У человечества ушли века на теорему Пифагора — как же ты хочешь, чтобы обычный школьник ее сам открыл?

Сальвиати. Я этого не хочу. Позволь мне ясно сказать: я сожалею о полном отсутствии в математической программе искусства и открытия, истории и философии, контекста и перспективы. Я не хочу сказать, что нотация, техника и накопление знаний не нужны. Нужны, конечно. У нас должно быть и то, и это. Если я возражаю против того, что маятник слишком далеко отклонился в одну сторону, это не значит, что я за то, чтобы он отклонился до конца в другую. Люди на самом деле лучше учатся, когда результат получается из процесса. Настоящая любовь к стихам приходит не от запоминания сотен поэм, а от написания собственных стихов.

Симплицио. Да, но прежде, чем писать стихи, ты должен выучить алфавит! Должно же все с чего-то начинаться. Сначала учатся ходить, потом — бегать.

Сальвиати. Да нет же, сначала тебе нужно знать, куда бежать. Дети учатся писать стихи и рассказы и одновременно письму и чтению. Рассказ шестилетнего — это чудесно, и орфографические и стилистические ошибки нисколько не умаляют этого чуда. Даже самые маленькие дети сочиняют песенки, хотя и не знают, в каком они размере и в какой тональности.

Симплицио. Но разве математика не отличается от музыки? Разве математика — не система символов, язык сам по себе, который надо выучить прежде, чем говорить на нем?

Сальвиати. Нет, это совершенно не так. Математика — не язык, а приключение. Разве музыканты «говорят на другом языке», сокращая свои идеи до маленьких черных нот? Если бы и так — это все равно не мешает карапузу и его песенке. Да, определенная система математической записи образовалась за века, но она не является самоважной. Математика частенько делается с друзьями за чашкой кофе на салфетках. Математика — это идеи, а идеи превосходят символы, которыми они записываются. Гаусс однажды заметил: «Нам нужны идеи, а не идиомы!»

Симплицио. Но разве не верно сказать, что одна из целей математического образования научить школьников думать логически точно, выработать «навыки математического мышления», как пишут в программе? Разве формулы и правила не оттачивают ума учеников?

Сальвиати. Нет, не «оттачивают». Если хочешь, система дает прямо противоположный эффект: она отупляет. Острота ума причиняется решением задач, а не заучиванием того, как это следует делать.

Симплицио. Ладно, согласен. А как быть с учениками, что идут в науку и в инженеры? Разве им не нужно обучение по стандартной программе? Не для того ли мы преподаем математику в школе?

Сальвиати. Много ли учеников станут писателями после уроков литературы? Мы учим литературе не для этого. Мы учим, чтобы просвещать, а не давать профтехобразование! Ведь самое важное умение и ученого, и инженера — умение мыслить творчески и независимо. А кому нужна эта дрессировка?!

Не нашли то, что искали? Воспользуйтесь поиском:

Основная цель обучения математике в школе – обеспечение учащихся прочными знаниями по школьному курсу математики. Порограмма по математике весьма обширна и соответствует различным направлениям современного образования. В последнее время возросла роль реальной математики особо выделяемой в нынешнем школьном курсе. Практическая значимость школьного курса математики обусловлена тем что её объектом являются пространственные формы и колличественные лотношения действительного мира. Математическая подготовка необходима для понимания принципов, устройства и использования современной техники. Математика важна для повседневной практической деятнельности человека. В современных условиях математика является языком науки и техники. с её помощью моделируются, изучаются и прогнозируются многие явления и процессы, происходящие в природе и обществе.

В силу этого математическая подготовка учащихся является необходимым условием ускорения научно=технического прогресса, от её качества непосредственно зависит научный, производственный, экономический потенциал. Математика имеет большие возможности для развития логического мышления учащихся, для применения логических приёмов мышления на практике. Изучая математику учащиеся овладевают умениями анализировать рассматриваемые воприсы, обобщать. выделять необходимые и достаточные условия, находить пути решения поставленной задачи. Изучение математики фомирует мышление учащихся, способствует развитию их речи. Особая направленность современного школьного курса математики – реальная математика, позволяет решать задачи возникающие в повседневной жизни.

Источник