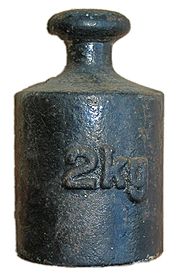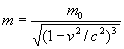Что такое масса покоя тела

Масса покоя

Ма́сса — одна из важнейших физических величин. Первоначально (XVII–XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. В современной физике понятие «количество вещества» имеет другой смысл, а под массой понимают два различных свойства физического объекта:

Теоретически, гравитационная и инертная масса равны, поэтому в большинстве случаев просто говорят о массе, не уточняя какую из них имеют в виду.

Масса тела не зависит от того, какие внешние силы и в какой момент на это тело действуют.

Содержание

Исследование единства понятия массы

Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел.

Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.

Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Следовательно, гравитационная масса пропорциональна инертной массе [1]

На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10 −3 ).. На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (3×10 −13 ).

Фактически, равенство гравитационной и инертной масс было сформулировано А. Эйнштейном в виде слабого принципа эквивалентности — составной части принципов эквивалентности, положенных в основу общей теории относительности. Существует также сильный принцип эквивалентности — по которому в свободно падающей системе локально выполняется специальная теория относительности. Он на сегодняшний день проверен со значительно меньшей точностью.

В классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В релятивистской механике масса неаддитивная величина, но тоже инвариантная, и хотя здесь под массой понимается абсолютная величина 4-вектора энергии-импульса, лоренц-инвариантная.

Определение массы

В СТО масса тела m определяется из уравнения релятивистской динамики [3] :

,

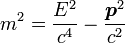
где E — полная энергия свободного тела, p — его импульс, c — скорость света.

Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то 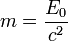— масса определяется энергией покоя.

Следует однако отметить, что частицы с нулевой инвариантной массой (фотон, гравитон…) двигаются в вакууме со скоростью света (c ≈ 300000 км/сек) и поэтому не обладают системой отсчёта, в которой бы покоились.

Масса составных и нестабильных систем

Инвариантная масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако, масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния.

Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: 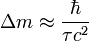. При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью равной означенному Δm.

Единицы массы

В системе СИ масса измеряется в килограммах. В системе СГС используются граммы. Иногда используются также другие единицы измерения массы.

Источник

Два определения массы, и почему я использую только одно из них

К сожалению, в процессе революции в науке, происходившей с понятиями пространства, времени, энергии, импульса и массы, Эйнштейн, кроме прочего, оставил после себя два различных и противоречащих друг другу определения массы. Из-за этого всё, что мы говорим и имеем в виду, можно интерпретировать двумя очень разными способами. При этом непосредственно в физике никакой путаницы нет. Специалисты точно знают, о чём идёт речь, и знают, как делать предсказания и использовать подходящие уравнения. Весь вопрос только в значении самого слова. Но слова важны, особенно когда мы беседуем о физике с людьми, не являющимися экспертами в этой области, и с учениками, для которых уравнения пока ещё не полностью понятны.

В своих статьях под «массой» я имею в виду свойство объекта, которое иногда ещё называют «инвариантной массой» или «массой покоя». Для нас с моими коллегами по физике частиц это просто старая добрая «масса». Термины «инвариантная масса» или «масса покоя» используются для того, чтобы уточнить, что вы имеете в виду под «массой», только если вы настаиваете на введении второй величины, которую вы тоже хотите называть «массой», и которую обычно называют «релятивистской массой». Специалисты по физике частиц избегают этой путаницы, совсем не используя концепцию «релятивистской массы».

Масса покоя лучше релятивистской в том, что первая масса – это свойство, по поводу величины которого соглашаются все наблюдатели. У объектов не так уж много подобных свойств. Возьмём скорость объекта: разные наблюдатели не согласятся по поводу скорости. Вот едет машина – как быстро она едет? С вашей точки зрения, если вы стоите на дороги, допустим, она едет со скоростью 80 км/ч. С точки зрения водителя машины она не двигается, а двигаетесь вы. С точки зрения человека, едущего навстречу машине, она может двигаться уже со скоростью в 150 км/ч. Выходит, что скорость – величина относительная. Нет смысла спрашивать о скорости машины, ибо нельзя получить ответ. Вы должны спрашивать, какова скорость объекта относительно определённого наблюдателя. У каждого наблюдателя есть право сделать это измерение, но разные наблюдатели получат разные результаты. Принцип относительности Галилея уже включал в себя эту идею.

Эти уравнения и их графическое представление подробно разобраны в другой статье.

Мне хочется дать вам понять причины, по которым специалисты по физике частиц используют эти уравнения и не считают, что уравнение E = mc 2 всегда выполняется. Это уравнение относится к тому случаю, в котором наблюдатель не двигается по отношению к объекту. Я попытаюсь сделать это, задав несколько вопросов, ответы на которых сильно различаются в зависимости от выбора значения слова «масса». Это поможет привлечь ваше внимание к большим проблемам в случае существования двух соперничающих определений массы и пояснить, почему в физике частиц гораздо проще работать с массой, не зависящей от наблюдателя.

Имеет ли частица света, фотон, массу или нет?

Но если вы имеете в виду релятивистскую массу – тогда да, имеет. У фотона всегда есть энергия, поэтому у него всегда есть масса. Ни один наблюдатель не увидит его безмассовым. Нулевая у него только инвариантная масса, также известная, как масса покоя. У каждого электрона будет своя масса, и у каждого фотона будет своя. Электрон и фотон, обладающие одной энергией, будут по этому определению обладать одной массой. У некоторых фотонов масса будет больше, чем у некоторых электронов, а у других электронов масса будет больше, чем у других фотонов. Что ещё хуже, для одного наблюдателя масса определённого электрона будет больше массы определённого фотона, а для другого всё может быть наоборот! Поэтому релятивистская масса приводит к путанице.

Действительно ли масса электрона больше, чем масса атомного ядра?

Если вы используете моё определение массы – то нет, никогда. Все наблюдатели согласятся с тем, что масса электрона в 1800 раз меньше массы протона или нейтрона, из которых состоит ядро.

Но если под массой подразумевать релятивистскую, то ответ будет: это зависит от ситуации. Масса электрона в покое меньше. У очень быстрого электрона – больше. Можно даже устроить всё таким образом, что масса электрона будет в точности совпадать с массой выбранного ядра. В общем можно сказать только то, что масса покоя электрона меньше, чем масса покоя ядра.

Есть ли масса у нейтрино?

При использовании моего понятия массы, ответ на этот вопрос был неизвестен с 1930-х годов, когда впервые была предложена концепция нейтрино, до 1990-х. Сегодня нам известно (почти наверняка), что у нейтрино масса есть.

Но если под массой подразумевать релятивистскую, то ответ будет: естественно, мы знали об этом с самого первого дня существования понятия «нейтрино». У всех нейтрино есть энергия, так что, как и у фотонов, у них есть масса. Вопрос лишь в наличии инвариантной массы.

У всех ли частиц одного типа – к примеру, у всех фотонов, у всех электронов, у всех протонов, у всех мюонов – одинаковая масса?

При использовании моего понятия массы, ответ на этот вопрос будет утвердительным. Все частицы одного типа обладают одинаковой массой.

Но если под массой подразумевать релятивистскую, то ответ будет: очевидно, нет. Два электрона, движущихся с разными скоростями, обладают разной массой. У них одинаковая только инвариантная масса.

Истинна ли старая формула Ньютона F = ma, соотносящая массу, воздействие и ускорение?

При использовании моего понятия массы, ответ будет: нет. В эйнштейновской версии относительности эта формула исправлена.

Но если под массой подразумевать релятивистскую, то ответ будет: это зависит от ситуации. Если вектора сила и движения частицы перпендикулярны, тогда да; в ином случае – нет.

Увеличивается ли масса частицы с увеличением скорости и энергии?

При использовании моего понятия массы, ответ будет: нет. Смотрите график выше. Разные наблюдатели могут назначить частице разную энергию, но все согласятся с её массой.

Но если под массой подразумевать релятивистскую, то ответ будет: да. Разные наблюдатели могут назначить частице разную энергию, и, следовательно, разные массы. Согласятся они только по поводу инвариантной массы.

Итак, мы по меньшей мере видим наличие лингвистической проблемы. Если мы не обозначим точно, какое из определений массы мы используем, мы получим совершенно разные ответы на простейшие вопросы физики. К сожалению, в большинстве книг для непрофессионалов и даже в некоторых учебниках для первого курса университета (!) авторы переключаются туда и сюда между этими терминами без пояснений. И самая распространённая путаница среди моих читателей связана с тем, что им сообщают два типа сведений о массе, противоречащих друг другу: один подходит для массы покоя, другой – для релятивистской. Очень плохо использовать одно слово для двух разных вещей.

Это, конечно, всего лишь язык. С языком можно делать всё, что угодно. Определения и семантика не имеют значения. Когда физик вооружён уравнениями, язык становится неидеальным носителем. Математика никогда не путается, и человек, понимающий математику, тоже не запутается.

Но для большинства людей и для начинающих студентов это кошмар.

Что делать? Один вариант – настаивать на использовании всех возможных терминов. Но из-за этого объяснения будут очень запутанными.

• Энергия покоящегося объекта = инвариантной массе умноженной на с 2 = релятивистской массе умноженной на с 2
• Масса движущегося объекта = инвариантной массе, как и раньше, но энергия = релятивистской массе помноженной на с 2 у него больше, чем ранее, из-за энергии движения.

Это слишком многословно. Мы с коллегами просто говорим:

Такой способ не менее содержателен, в нём используется меньше различных концепций и определений, он избегает двух противоречивых значений слова «масса», одно из которых не меняется с движением, а другое – меняется.

С точки зрения лингвистики, семантики и концепций, необходимо избегать понятия «релятивистская масса» и убрать слова «инвариантная» и «покоя» из определений «инвариантная масса» и «масса покоя» потому, что «релятивистская масса» – бесполезная концепция. Это просто другое название для энергии частицы. Использовать понятие «релятивистской массы» – это то же самое, как настаивать на термине «красновато-синий». Если я начну настаивать на использовании термина «красновато-синий» для описания изюма, вы возразите: но у нас уже есть слово для этого цвета: пурпурный. Что с ним не так? И ещё вы можете сказать: «Говорить, что цвет изюма – это разновидность синего цвета, неправильно и это запутывает. Можно сделать вывод, что цвет изюма немного похож на цвет неба, а на самом деле они отличаются». Примерно в таком же ключе релятивистская масса помноженная на с 2 — это просто другое название энергии (для которой у нас уже есть подходящее слово), и описывать энергию так, будто это что-то вроде массы, значит, запутывать читателя.

Величина справа явно не нуждается в новом названии, поскольку это явно ни E, ни p – она не сохраняется, как E и p, но она не зависит от наблюдателя (в отличие от E и p!)

Понятие «релятивистской массы» появилось не на пустом месте и не из какой-то глупости. Его ввёл сам Эйнштейн, и не зря, поскольку он имел дело с отношениями между энергией системы объектов и массой этой системы. Но хотя понятие релятивистской массы пропагандировалось и распространялось другими знаменитыми физиками того времени, сам Эйнштейн, судя по всему, отбросил такой способ мышления, и тоже не зря. Так же поступило сообщество современных специалистов по физике частиц.

Источник

Что такое масса покоя тела

Масса покоя или инертная масса?

Исключение из современных учебников физики инертной массы и замена ее массой покоя представляется ошибкой. Эта тема была поднята автором в статье [1,2]. Здесь приведены дополнительные рассуждения в подтверждение такого тезиса.

Конец 20-го века ознаменовался великой путаницей с физическим понятием «масса тела».

В начале века, до создания теории относительности, было все ясно. Массой тела, m, называлось количество вещества тела, и в то же время масса являлась мерой инертности тела. Инертность тела определяет его «количество движения» при заданной скорости v движения, то есть коэффициент пропорциональности в формуле

Но массу как меру инертности тела можно определять и с помощью формулы

чем больше масса, тем меньше ускорение тела при заданной силе. Значение массы по формулам (1) и (2) получалось одно и то же, потому что формула (2) является следствием формулы (1), если инертная масса не зависит от времени и скорости.

То же значение массы можно было получить, взвесив тело, то есть измерив силу притяжения к земле или к любому другому заданному телу (масса которого обозначена M). В законе тяготения Ньютона фигурирует та же самая масса m,

, (3)

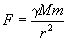
но тут она называется гравитационной (пассивной) массой. В этом выражается эквивалентность инертной и гравитационной массы. Благодаря этой эквивалентности ускорение свободного падения, как известно, не зависит от природы и массы тела:

(4)

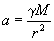
Однако при создании теории относительности выяснилось, что никакое тело нельзя разогнать до скорости света, потому что при приближении скорости тела к скорости света ускорение тела уменьшается до нуля, как бы ни была велика ускоряющая сила. Другими словами, выяснилось, что инертность тела возрастает до бесконечности при приближении его скорости к скорости света, хотя «количество вещества» тела, очевидно, остается при этом неизменным.

Выскажемся точнее по поводу увеличения инертности тела. Теория относительности показала, что импульс тела P при любых скоростях остается параллелен скорости v. Поэтому формулу P = mv можно сохранить неизменной при больших скоростях, если принять, что коэффициент m, то есть инертная масса, увеличивается с ростом скорости по закону

, (5)

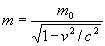
то есть для импульса тела справедливо выражение

. (6)

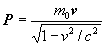
Для того, чтобы подчеркнуть, что инертная масса m зависит от скорости, ее называют иногда «релятивистской» массой: она оказывается различной с точки зрения различных наблюдателей, если эти наблюдатели движутся друг относительно друга. Однако существует выделенное значение инертной массы, именно, значение, которое наблюдает неподвижный относительно тела наблюдатель. Другими словами, масса покоя является выделенным значением инертной массы. Такое свойство инертной массы аналогично свойству времени: одни и те же часы имеют разную скорость хода с точки зрения различных наблюдателей. Однако существует собственная скорость хода часов.

При желании проверить формулу (6) вы должны измерить скорость v тела, а потом измерить импульс тела. Для этого следует затормозить тело некоторой преградой, все время замеряя силу F(t), с которой при торможении тело будет действовать на преграду, а потом проинтегрировать. Импульс, как известно, равен

(7)

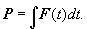
Эта процедура, по сути, задает операционное определение инертной массы.

Заметим, что формулы (5) и (6) остаются справедливыми и для объекта, у которого нет массы покоя, m₀ = 0, например, для фотона или нейтрино (если предположить, что масса покоя нейтрино равна нулю). Такие объекты обладают инертной массой и импульсом, но должны двигаться со скоростью света, их нельзя остановить, они исчезают при остановке. Тем не менее, несмотря на постоянство скорости движения, величина их инертной массы оказывается различной с точки зрения различных наблюдателей. Однако в этом случае не существует какого либо выделенного значения инертной массы. Либо, можно сказать, выделенное значение равно нулю.

Увеличение инертности тела при больших скоростях мы объяснили уменьшением ускорения при большой скорости. При этом мы сослались на формулу (2). И это допустимо. Однако именно в силу увеличения инертной массы с ростом скорости тела формула (2) при некоторых условиях изменяет свой вид. Это объясняется тем, что при фиксированном ускорении сила, если она имеет составляющую вдоль скорости, должна обеспечить не только возрастание скорости уже имеющейся массы

, (5)

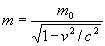
она должна обеспечить возрастание самой массы:

. (8)

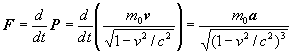
Если сила перпендикулярна скорости и, значит, не изменяет величину скорости и инертной массы, то формула F = ma сохраняет свой вид:

. (9)

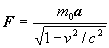
Последнее обстоятельство позволило Р. Фейнману предложить простой способ операционного определения инертной массы, основанный на формуле (9) и справедливый для любой скорости. «Массу можно измерить так: просто привязать предмет на веревочке, крутить его с определенной скоростью и измерять ту силу, которая необходима, чтобы удержать его.» [4]

3. Гравитационная масса

Одновременно теория относительности показала, что не только инертность тела, но и его вес увеличивается с ростом скорости, причем по тому же закону (5) в соответствии с эквивалентностью инертной и гравитационной массы. Поэтому формула (8) для тела, падающего вниз со скоростью v, выглядит, грубо говоря, так:

= .

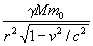
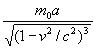
Точная формула для ускорения может быть получена в рамках общей теории относительности, как показано в конце статьи:

, . (10)

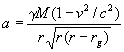
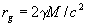
Эта формула является релятивистским аналогом формулы (4).

Эта знаменитая формула Эйнштейна провозглашает эквивалентность инертной массы и энергии. Два, доселе различных понятия, соединяются в одно.

Заметим, что формула (12), как и формулы (5) и (6) остается справедлива и для объекта, у которого нет массы и энергии покоя, m₀ = 0.

При желании проверить формулу (11) и одновременно убедиться в справедливости теории относительности вы должны измерить инертную массу и массу покоя тела как было объяснено выше, и, кроме того, измерить кинетическую энергию тела. Для этого следует при торможении тела упомянутой преградой все время замерять силу, с которой тело будет действовать на преграду в процессе торможения в функции перемещения l преграды, F(l), а потом проинтегрировать. Кинетическая энергия, равная, как известно, в данном случае работе, вычисляется по формуле

.

. (13)

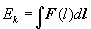
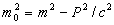
Для частиц с нулевой массой покоя получаем mc = P или E = Pc.

При объединении нескольких тел в систему тел, как известно, их импульсы и их инертные массы складываются. Для двух тел это выглядит так:

Другими словами, импульс и инертная масса аддитивны. Не так обстоит дело с массой покоя. Из формул (13), (14) следует, что масса покоя пары тел с массами покоя m₀₁, m₀₂ равна не сумме m₀₁ + m₀₂, а сложному выражению, зависящему от импульсов P₁, P₂:

. (15)

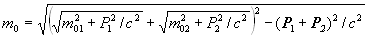
Таким образом, масса покоя, вообще говоря, не аддитивна. Например, пара фотонов, не имеющих массу покоя, имеет массу покоя, если фотоны летят в разные стороны, и не имеет массу покоя, если фотоны летят в одну и ту же сторону.

Тем не менее, все три величины, P, m, m₀, подчиняются закону сохранения, то есть не изменяются со временем для замкнутой системы.

Однако ввиду неаддитивности массы покоя, на наш взгляд, нецелесообразно рассматривать массу покоя системы тел. Имеет смысл говорить лишь о сумме масс покоя отдельных тел системы. В действительности именно так поступают на практике. Когда говорят, что при неупругих соударениях увеличивается масса покоя, имеют ввиду не массу покоя системы, которая удивительным образом сохраняется неизменной при соударениях благодаря неаддитивности, а сравнивают именно сумму масс покоя тел до столкновения и массу покоя после столкновения. Точно так же, когда говорят о дефекте массы покоя при ядерных реакциях, имеют в виду не массу покоя, определяемую формулой (15), а сумму масс покоя частей системы.

На наш взгляд, инертную массу следует называть массой и обозначать m, как это и делалось в настоящей статье.

7. Психологическая подоплека

К сожалению, большое количество физиков считает массу покоя главной и обозначает ее m а не m₀, а инертную массу дискриминирует и оставляет без обозначения, что вносит дополнительную путаницу, поскольку из-за этого порой бывает трудно понять, о какой массе идет речь.

Эти физики соглашаются, например, с тем, что масса газа увеличивается при нагревании, потому что увеличивается содержащаяся в нем энергия, но психологический барьер мешает им попросту объяснить это увеличение ростом массы отдельных молекул вследствие увеличения их тепловой скорости.

Сторонники массы покоя, видимо, не в состоянии принять идею инертной, релятивистской массы так же, как ранее противники теории относительности не могли принять относительность времени. Ведь время жизни астронавта или нестабильной частицы изменяется так же, как изменяется их инертная масса: 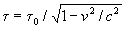. Здесь уместно процитировать М. Планка: «Великая научная идея редко внедряется путем постепенного убеждения и обращения своих противников, редко бывает, что Савл становится Павлом. В действительности дело происходит так, что оппоненты постепенно вымирают, а растущее поколение с самого начала осваивается с новой идеей.» [11] К сожалению, великая идея релятивистской массы тщательно изолируется от молодежи. На данный момент статья [1, 2] отклонена редакциями следующих журналов: «Известия вузов. Физика», «Квант», «American Journal of Physics», «Physics Education» (Bristol), «Physics Today».

8. Шварцшильдовское пространство

Мы получим здесь формулу (10), рассмотрев пространство-время Шварцшильда общей теории относительности с выражением для интервала s [12] :

.

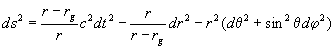
Уравнения радиальной геодезической линии могут быть получены по общей формуле, использующей коэффициенты связности :

, (16)

. (17)

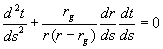
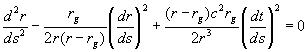
Первый интеграл уравнения (16) легко находится:

. (18)

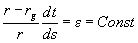
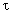
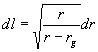
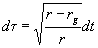
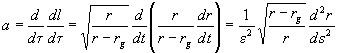
Запишем теперь выражение для ускорения a, учитывая (18) и то, что соотношения между расстоянием l и временем , с одной стороны, и координатами r, t, с другой, даются формулами

, :

.

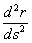
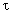
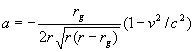
Выразив таким образом ускорение a через , мы можем теперь воспользоваться уравнением (17), а затем, вернувшись к l и , получить окончательно

, . (10)

9. Taylor E. F., Wheeler J. A. Spacetime Physics. √ San Francisco: Freeman, 1966.- 631c. Русский перевод: Тейлор Э. Ф., Уилер Дж. А. Физика пространства-времени. √ М.: Мир, 1971.- 612c.

Источник