Что такое масса формула

Формулы массы в физике. Инерционная и гравитационная массы. Относительная атомная масса. Масса и энергия

Масса является одним из важных свойств материи. Это понятие применяют при решении задач различного характера, начиная от проблем в механике и заканчивая химическими расчетами. Рассмотрим в статье, с помощью каких формул массу в физике можно рассчитать.

Что это такое?

Прежде чем приводить формулы массы в физике, дадим ей определение. Этим термином называется физическая величина, которая пропорциональна количеству материи, заключенной в данном теле. Следует не путать ее с количеством вещества, которое выражается в молях. Масса в СИ вычисляется в килограммах. Другими ее единицами являются тонны и граммы.

Вам будет интересно: Слово «кворум». Значение и происхождение термина. Нюансы определения

Масса бывает двух важных видов:

Первый вид рассматриваемой физической величины характеризует инерционные свойства тела, то есть способность некоторой силы изменять скорость тела, а также кинетическую энергию, которой оно обладает.

Гравитационная масса связана с интенсивностью притяжения между любыми телами. Она играет важную роль в космосе, поскольку благодаря притяжению между звездами и планетами существует наша галактика и наша Солнечная система. Однако гравитационная масса проявляет себя и в повседневной жизни в виде наличия у всех тел некоторого веса.

Формулы для инерции

В физике формула нахождения массы инерционной имеет следующий вид:

Помимо записанного выражения, следует привести еще одну формулу нахождения массы в физике, которая связана с явлением инерции. Эта формула имеет вид:

Формула для гравитации

Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений в XVII веке обобщил Исаак Ньютон в рамках закона всемирного тяготения. Согласно этому закону, два тела, которые имеют массы m1 и m2, друг к другу притягиваются с такой силой F:

Если в данное выражение подставить значение массы нашей планеты и ее радиус, тогда мы получим следующую формулу массы в физике:

Весы, которыми человек пользуется в быту (механические, электронные), показывают массу тела, однако измеряют его вес. Перевод между этими величинами является лишь вопросом калибровки прибора.

Плотность и объем

Объем представляет собой некоторую часть пространства, которая ограничена поверхностью тела. Измеряется он в кубических единицах длины, например, в м3.

Формула массы вещества через объем и плотность записывается так:

Чем больше объем тела и чем выше его плотность, тем большей массой оно обладает. В связи с этим фактом полезно вспомнить знаменитую загадку про то, что имеет большую массу: 1 тонна пуха или 1 тонна железа. В отсутствии выталкивающей архимедовой силы массы обоих веществ равны. Пух имеет гораздо меньшую плотность, чем железо, однако разница в плотности компенсируется аналогичной разницей в объеме.

Относительная

Понятие об относительной массе применяется в атомной физике и в химии. Поскольку массы атомов и молекул имеют очень маленькие значения (≈10-27 кг), то оперировать ими на практике при решении задач оказывается крайне неудобно. Поэтому сообществом ученых было решено использовать так называемую относительную массу, то есть рассматриваемая величина выражается в единицах массы по отношению к массе известного эталона. Этим эталоном стала 1/12 массы атома углерода, которая равна 1,66057*10-27 кг. Соответствующая относительная величина получила название атомной единицы (а. е. м.).

Формулу относительной массы M можно записать так:

M = 26,5606 * 10-27 / (1,66057 * 10-27) = 15,9949.

Поскольку а. е. м. является относительной величиной, то она не имеет размерности.

Удобство применения этого термина на практике заключается не только в небольших и целых значениях этой единицы измерения. Дело в том, что значение а. е. м. совпадает по величине с молярной массой, выраженной в граммах. Последняя представляет собой массу одного моль вещества.

Энергия

Выше были приведены разные формулы, как найти массу в физике. Завершая статью, хотелось бы отметить связь массы и энергии. Это связь носит фундаментальный характер, который отражает пространственно-временные свойства нашей Вселенной. Соответствующая формула массы в физике, полученная Альбертом Эйнштейном, имеет вид:

Квадрат скорости света c является коэффициентом перевода между массой и энергией. Это выражение говорит о том, что обе величины, по сути, являются одной и той же характеристикой материи.

Записанное выражение было подтверждено экспериментально при изучении ядерных реакций и реакций элементарных частиц.

Источник

Формула массы тела

Определение и формула массы тела

В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.

Масса – аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна сумме масс всех отдельных частей системы (m_i):

В классической механике считают:

Инертная масса

Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:

где масса определяет инертные свойства материальной точки (инертная масса).

Гравитационная масса

Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.

Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой тяжести (F_t) избранного тела:

где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.

Формула расчета массы через плотность тела

Масса тела может быть рассчитана как:

Масса в специальной теории относительности

В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:

где E – полная энергия свободного тела, p- импульс тела, c – скорость света.

Релятивистская масса частицы определяется формулой:

где m₀ – масс покоя частицы, v – скорость движения частицы.

Основной единицей измерения массы в системе СИ является: [m]=кг.

Примеры решения задач

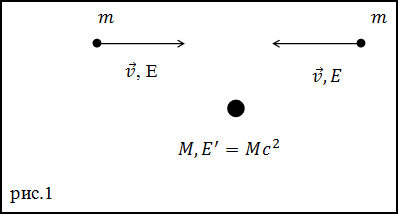
Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:

В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией. По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:

где E₁ – энергия первой частицы до удара, E₂ – энергия второй частицы до соударения.

Закон сохранения энергии запишем в виде:

Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:

Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Какова масса 2м 3 меди?

Решение. Будем считать, что медь однородна и для решения задачи используем формулу:

$m=8900 \cdot 2=17800$ (кг)

Источник

Масса в физике

Содержание:

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Масса

Всякое тело притягивается Землёй. Сила, с которой Земля притягивает тело, называется весом тела. С понятием веса тела тесно связано другое, более общее
понятие — масса тела.

Массой тела называется количество вещества, содержащегося в этом теле.

Масса литра воды в 1000 раз больше массы 1 см3 воды, масса бревна во много раз больше массы полена из такого же дерева. Словом, массы однородных тел тем больше, чем больше объёмы этих тел. При равенстве их объёмов равны и массы. Так, например, массы двух одинакового объёма кусков железа равны между собой. Если положить эти куски на чашки весов, то они окажутся в равновесии. Это даёт нам возможность измерять массы тел взвешиванием.

Рис. 98. Измерение массы тела.

Массы двух тел равны, если эти тела одинаково притягиваются Землёй в одном и том же месте,
т. е. если они уравновешивают друг друга на чашках рычажных весов. При этом совершенно безразлично, из каких веществ состоят эти тела. Если массу одного из этих тел принять за единицу массы, то и масса другого тела, которое уравновешивается первым, будет также равна единице массы.

За единицу массы принята масса платинового цилиндра, хранящегося в Сере (близ Парижа). Эта масса называется килограммом. В отличие от единицы силы, обозначаемой кГ, единица массы сокращённо обозначается кг.

В физике за единицу массы принимают 0,001 кг. Эта единица называется граммом (сокращённое обозначение—г).

В практике эталоны масс изготовляют в виде гирь различной величины.

Чтобы измерить массу тела, надо положить на одну чашку весов это тело, а на другую—гири. При равновесии весов масса тела равна массе гир. На рисунке 98 показано, что масса тела равна 0,5 кг.

Второй закон Ньютона

Во втором законе Ньютона устанавливается связь между силой, действующей на тело, массой тела и ускорением, с которым движется это тело.

Рис. 99. Прибор для установления зависимости ускорения от силы, действующей на тело.

Рассмотрим сначала, как зависит ускорение одного и того же тела от величины силы, действующей на тело. Проделаем следующий опыт (рис. 99). К тележке, которая может (с малым трением) двигаться по столу, прикреплён динамометр. К другому концу динамометра прикреплена нитка с грузом М, переброшенная через блок. По показаниям динамометра мы сможем определить силу, действующую на тележку. Пользуясь капельницей, отметим пути, пройденные тележкой при ускоренном движении за различные промежутки времени под действием постоянной силы. Измерения показывают, что пути эти пропорциональны квадратам времён. Таким образом, движение под действием постоянной силы есть равноускоренное движение.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле определяем ускорение а.

Будем подвешивать к концам нити различные грузы, каждый раз измеряя динамометром силу и вычисляя соответствующее этой силе ускорение тележки.

Результаты таких измерений и вычислений отражены в таблице.

Из таблицы видно, что с увеличением силы в 1,5 раза ускорение увеличивается тоже в 1,5 раза; если сила увеличивается в 2 раза, в 2 раза увеличивается и ускорение, и т. д., т. е. ускорение тележки прямо пропорционально силе, действующей на тележку.

Математически это можно записать в виде формулы:

Чтобы установить, как зависит ускорение от массы тела, будем действовать на тележку какой-нибудь постоянной силой.

Нагружая тележку гирями, изменим массу движущихся тел.

Ускорение, получаемое тележкой, будем вычислять так же, как и в первом случае.

Результаты опытов снова занесём в таблицу.

Данные таблицы показывают, что при неизменной силе увеличение массы тела в два раза приводит к уменьшению ускорения в два раза, и наоборот, при уменьшении массы в два раза ускорение увеличивается в два раза, т. е. ускорение тележки с грузами обратно пропорционально их общей массе. Математически этот вывод можно
выразить формулой:

Итак, результаты опытов показывают, что ускорение, с которым движется тело, пропорционально действующей на тело силе и обратно пропорционально массе этого тела.

Кроме того, ускорение тела совпадает с этой силой по направлению.

Этот вывод, как показал Ньютон, имеет всеобщий характер; он носит название второго закона Ньютона.

Во втором законе Ньютона говорится о действии одной силы. Но практически на тело всегда действуют несколько сил. Нам уже известно, что в расчётных целях мы действие нескольких сил можем заменить действием одной силы — равнодействующей. Поэтому в случае, когда на тело действуют несколько сил, под силой, вызывающей ускорение тела, подразумевается их равнодействующая.

Второй закон Ньютона математически можно выразить в виде следующей формулы:

откуда

Величина силы равна произведению массы тела на ускорение.

Таким образом, второй закон Ньютона позволяет вычислить величину силы, если известна масса тела и ускорение, с которым оно движется.

В частности, на основании второго закона Ньютона вес тела Р можно выразить через массу этого тела т и ускорение свободного падения g:

Из сопоставления формулы F=ma и P=mg видно, что

т. е. ускорение движения тела под действием некоторой силы во столько же раз больше или меньше ускорения свободного падения, во сколько раз действующая сила больше или меньше веса тела.

При решении задач с помощью указанного выше отношения однородные величины должны быть выражены в одних и тех же единицах.

Пример. Санки с седоком весят 70 кГ и скатываются с горы с ускорением Определить силу, движущую санки.

Из формулы определим F:

Масса — мера инертности тела

Первый закон Ньютона утверждает, что всякое тело обладает свойством инерции, иначе говоря, всякое тело инертно. Какова мера инертности тела? Обратимся к следующему примеру.

Пусть по горизонтальному пути с одинаковой скоростью движутся два вагона, один пустой, другой гружёный. Пусть на каждый из них одновременно начали действовать одинаковые силы, тормозящие их движение. Какой из этих вагонов будет дольше сохранять своё движение? Опыт показывает, что гружёный вагон будет двигаться дольше, следовательно, можно сказать, что он обладает и большей инертностью. Но масса гружёного вагона больше массы пустого; отсюда следует, что чем больше масса тела, тем более оно инертно.

Рис. 100. Масса наковальни значительно больше массы молота.

Этот вывод непосредственно вытекает из второго закона Ньютона. Действительно, по второму закону Ньютона т. е. ускорение обратно пропорционально массе, а так как масса гружёного вагона больше массы пустого, то и ускорение его движения будет меньше (ускорение направлено против движения). Следовательно, гружёный вагон дольше будет сохранять своё движение.

Итак, масса тела является мерой его инертности.

Из второго закона Ньютона следует,что любая сколь угодно малая сила может вызвать ускоренное движение тела.

Не противоречит ли этому то, что мы иногда, толкая тяжёлый предмет, не можем сдвинуть его с места? Нисколько не противоречит. Дело в том, что между предметом и полом существует трение, и нам, чтобы привести его в движение,надо преодолеть это трение, а для этого сила, с которой мы толкаем предмет, должна быть больше силы трения, что не всегда бывает.

Изменение скорости тела зависит от массы тела и от времени действия силы на тело. Это видно хорошо на следующем опыте.

Положим на одну чашку весов тяжёлую плиту и уравновесим её гирями или каким-нибудь другим грузом. Если резко ударить небольшим молоточком по плите, то равновесие весов не нарушится.

Если же положить на чашки весов тела с малой массой, то уже при самом незначительном ударе равновесие весов нарушится.

Чем больше масса тела, тем меньшее изменение скорости вызывает действующая на него сила. Это учитывается в технике.

Рис. 101. Машина на массивном фундаменте.

Так, например, для уменьшения сотрясений от ударов делают массивными и прочно соединяют с землёй мостовые „быки“ и упоры; массивными делают наковальни: относительные размеры молота и наковальни видны на рисунке 100. По этой же причине станки и машины делают массивными и устанавливают их на массивные фундаменты. На рисунке 101 изображена машина, установленная на массивном основании.

Нам известен способ определения массы тела с помощью взвешивания тела на рычажных весах. Второй закон Ньютона даёт нам другой способ определения массы — как меры инертности тела по величине силы и ускорению:

Опытом проверено, что оба эти способа определения массы тела (по весу и по инертности) дают совершенно одинаковые результаты.

Система единиц измерения механических величин

Чтобы применять формулы для числовых расчётов, необходимо установить, в каких единицах измеряются физические величины.

Физические законы связывают физические величины определёнными зависимостями. Поэтому если произвольно выбрать единицы для измерения некоторых величин, то единицы для измерения других величин получатся на основе соответствующих законов. Например, в формуле s = vt дана зависимость между тремя величинами. Если мы произвольно выберем единицы каких-нибудь двух величин, то единица третьей величины определится из этого уравнения. Условившись, например, измерять путь в метрах, а время в секундах, мы должны будем измерять скорость в

Зависимости, существующие между физическими величинами, дают возможность составить такую совокупность единиц, в которой для измерения механических величин достаточно выбрать произвольно три единицы: единицу длины, единицу массы, или силы, и единицу времени; такая совокупность единиц называется системой единиц.

Выбранные произвольно единицы системы называются основными единицами, а все другие — производными единицами.

В физике принята система единиц, в которой основными единицами являются: единица длины—1 см (сотая часть международного метра), единица массы— 1 г (тысячная часть международного килограмма) и единица времени—1 сек ( средних солнечных суток, измеряемая весьма точными часами, которые систематически проверяются астрономическими наблюдениями) (Солнечные сутки—промежуток времени между двумя следующими друг за другом полуднями. Так как продолжительность солнечных суток в разные времена года несколько различна, то в практику введены средние солнечные сутки, продолжительность которых равна средней длительности суток за год).

Эта система называется системой единиц CGS (по первым буквам слов—сантиметр, грамм, секунда).

Единица скорости в этой системе единица ускорения

Полагая в формуле F=ma второго закона Ньютона m = 1 г, получим единицу силы в системе CGS:

За единицу силы в системе CGS принимается такая сила, под действием которой масса в 1 г движется с ускорением, равным Эта единица называется диной (сокращённо дн).

В системе единиц, применяемой в настоящее время в СССР при электрических и магнитных измерениях, за основные единицы принимаются:

единица длины — 1 м,

единица массы — 1 кг,

единица времени — 1 сек,

единица тока — 1 ампер.

Сокращённо мы эту систему единиц будем называть MKSA (по первым буквам слов—метр, килограмм, секунда, ампер).

Единицей силы в системе MKSA будет такая сила, под действием которой масса в 1 кг движется с ускорением Эта единица называется ньютон (сокращённо н). Таким образом,

Вычислим, сколько в одном ньютоне содержится дин. или
В практике довольно широко распространена так называемая техническая система единиц. В этой системе основными единицами являются:

единица времени—1 сек.

Единица массы в этой системе единиц является производной и может быть определена из равенства т. е. единицей массы в технической системе единиц является масса, которая под действием силы в 1 кГ движется с ускорением

Сокращённое обозначение этой единицы—т. е. м. Таким образом,

Между различными единицами массы и силы существуют следующие соотношения:

1 кГ есть сила, с которой Земля притягивает массу в 1 кг и сообщает ей ускорение Отсюда: или округлённо:

Так как то 1 кГ = 9,8 н.

Примеры решения задач на второй закон Ньютона

1. Постоянная сила, равная 2 кГ, действует на тело, вес которого 19,6 кГ. С какой скоростью будет двигаться тело в горизонтальном направлении по прошествии 5 сек., если начальная скорость движения равна нулю?

Расчёты ведём в системе CGS.

Дано: F = 2 кГ=2*980000 дн = 1960000 дн;

m=19600 г; t = 5 сек. Найти

Под действием постоянной силы тело будет двигаться равноускоренно. Скорость этого тела определим по формуле:

Время t дано по условиям задачи.

Ускорение найдем на основании второго закона:

Ответ:
2. Тело весом 98 кГ движется со скоростью, равной
Какую силу надо приложить, чтобы остановить это тело в течение 5 мин.? Расчёты провести в технической системе единиц.

Дано: Р = 98 кГ; t = 300 сек. Найти F.

Искомую силу найдём на основании второго закона:

Под действием этой силы тело будет двигаться равнозамедленно, отрицательное ускорение его а определим по формуле;

Так как то

и

По второму закону Ньютона Р = mg, откуда

Ответ.

3. На тело, движущееся с начальной скоростью в подействовали силой в 10 Г в направлении движения, после чего тело прошло за 5 сек. путь в 200 м. Определить вес тела. Расчёты провести в системе CGS.

Вес тела в системе CGS, выражаемый в динах, найдётся на основании второго закона Ньютона:

Надо найти массу в граммах. Для этого воспользуемся тем F же вторым законом, ускорение а по условиям задачи вычислим по формуле:

Ответ.

При решении физических задач мы производим математические действия не только с числовыми значениями величин, но и над их наименованиями. Если предварительно все величины, указанные в задаче, выразить в единицах одной системы единиц и правильно применить соотношения, существующие между физическими величинами, то ответ всегда получится в единицах этой системы. Это позволяет нам не загромождать вычисления наименованиями единиц; достаточно указать наименование величины только в окончательном результате.

Пример. Тело массой 0,01 кг, двигаясь равноускоренно без начальной скорости, за 1 мин. прошло в горизонтальном направлении путь, равный 18 м. Определить силу, действующую на тело.

Дано: m = 0,01 кг; t = 1 мин.; s = 18 м. Найти F.

Выражаем все данные в задаче величины в единицах одной системы, например в системе CGS.

m = 10 г; t = 60 сек.; s = 1800 см.

По второму закону Ньютона F = ma. (1)

Масса дана, ускорение а находим по формуле пути равноускоренного движения: откуда

Подставим значение а из равенства (2) в равенство (1), получим:

Подставляя численные значения величин в равенство (3), определим величину силы F:

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник