Что такое логическая переменная

Что такое логическая переменная

Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

1. Логические выражения и логические операции

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).

Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.

Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.

Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.

С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.

Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.

В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.

Существуют разные варианты обозначения истинности и ложности логических переменных:

Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Введем перечисленные логические операции.

В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Источник

Логические переменные и логические функции

Вы будете перенаправлены на Автор24

Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности логической функции.

Логическая функция может быть задана аналитическим (при помощи формул) или табличным способом.

Логическая функция, представленная с помощью инверсии, дизъюнкции и конъюнкции называется нормальной.

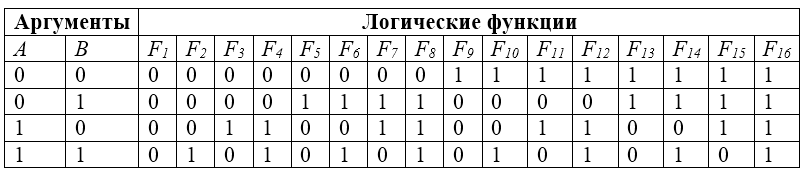
Рисунок 1. Логические функции двух переменных

Готовые работы на аналогичную тему

Среди перечисленных выше шестнадцати логических функций от двух переменных можно выделить такие логические функции, с помощью которых выражаются другие логические функции. Операция замены одной логической функции на другую в алгебре логики (булевой алгебре) называется операцией суперпозиции или метод суперпозиции.

Функцию Шеффера методом суперпозиции можно выразить при помощи функций отрицания и дизъюнкции, используя закон Де Моргана:

Наиболее широко в качестве базовых функций используют три логических функции: конъюнкцию, дизъюнкцию и отрицание. В приведенном примере логическая функция Шеффера выражена через базовые функции и представлена в нормальной форме.

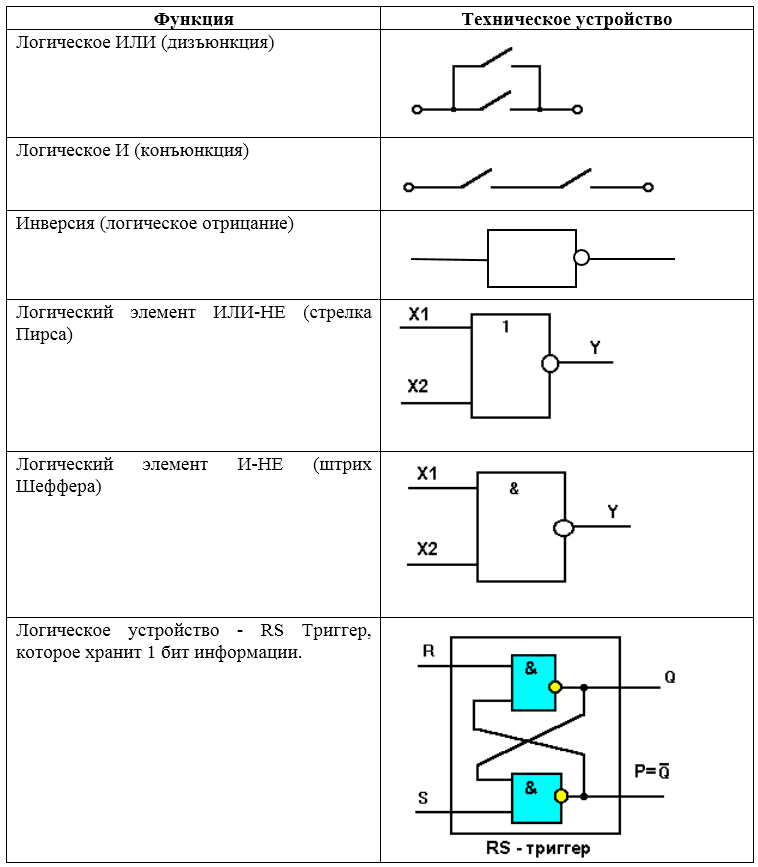
Каждой базовой функции соответствует техническое устройство, реализующее эту логическую функцию.

Рисунок 2. Соответствие базовой функции и технического устройства

Наборы И-НЕ и ИЛИ-НЕ являются функционально полными или базисными наборами.

При помощи набора базовых функций и соответствующих им технических устройств, которые реализуют эти логические функции, создаются любые логические устройства или системы.

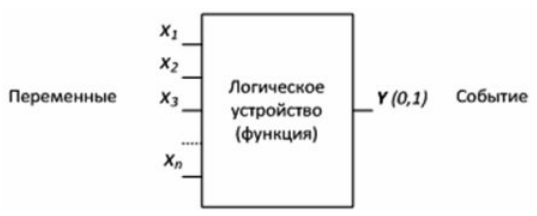
Логическое устройство имеет сколь угодное количество входов и только один выход (См. рис.3).

Рисунок 3. Схематичное представление логического устройства

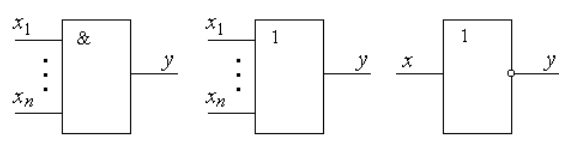
Рисунок 4. Условное обозначение логических элементов на электрических схемах: И (а), ИЛИ (б), НЕ (в)

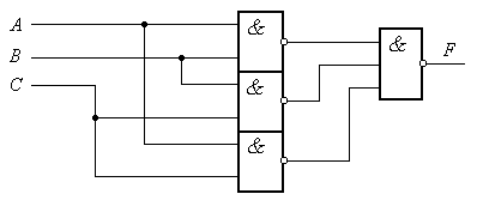
Приведем пример реализации функции при помощи инверсии и отрицания (в базисе И-НЕ).

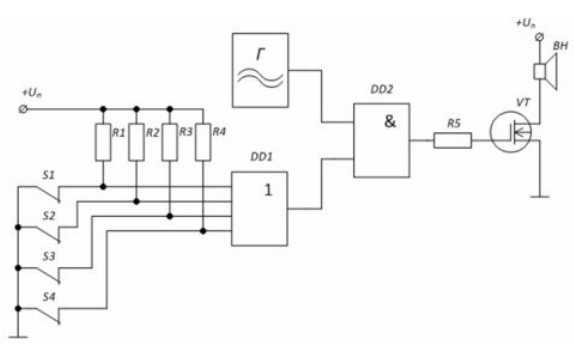
Рисунок 6. Пример схемы охранной сигнализации

Источник

4.1. Логические переменные и логические операции

4.1. Логические переменные и логические операции

Информация (данные, машинные команды и т. д.) в компьютере представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, может принимать значения 1 (высокий уровень электрического напряжения) и 0 (низкий уровень электрического напряжения) и рассматривается как импульсный сигнал, который математически может быть описан в виде двоичной переменной, принимающей также значения 0 или 1. Для решения различных логических задач, например, связанных с анализом и синтезом цифровых схем и электронных блоков компьютера, широко используются логические функции и логические операции с двоичными переменными, которые называются также логическими переменными.

Логические переменные изучаются в специальном разделе математики, который носит название алгебры логики (высказываний), или булевой алгебры. Булева алгебра названа по имени английского математика Джорджа Буля (1815–1864), внесшего значительный вклад в разработку алгебры логики. Предметом изучения алгебры логики являются высказывания, при этом анализу подвергается истинность или ложность высказываний, а не их смысловое содержание. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А, В, С, D,… и т. д. Составные высказывания на естественном языке образуются с помощью союзов. В алгебре логики эти союзы заменяются логическими операциями. В соответствии с алгеброй логики любое составное высказывание можно рассматривать как логическую функцию F(А, В, С, …), аргументами которой являются логические переменные А, В, С… (простые высказывания). Логические функции и логические переменные (аргументы) принимают только два значения: «истина», которая обозначается логической единицей – 1 и «ложь», обозначаемая логическим нулем – 0. Логическую функцию называют также предикатом.

Действия, совершаемые над логическими переменными для получения определенных логических функций, называются логическими операциями. В алгебре логики используются следующие логические операции.

1. Логическая операция ИНВЕРСИЯ (отрицание). В естественных языках соответствует словам неверно, ложь или частице не, в языках программирования обозначается Not, в алгебре логики обозначается

Инверсия каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Математическая запись данной операции для логической переменной А будет иметь вид:

Конъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда являются истинными простые высказывания, образующие составное высказывание.

Математическая запись данной операции для логических переменных Д В, С, … будет иметь вид:

3. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение). В естественных языках соответствует союзу или, в языках программирования обозначается Or, в алгебре логики обозначается V.

Дизъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда хотя бы одно из образующих его высказываний является истинным.

Математическая запись данной операции для логических переменных A, В, С, … будет иметь вид:

Импликация каждым простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда первое высказывание истинно, а второе высказывание ложно.

Математическая запись данной операции для двух логических переменных А и В будет иметь вид:

Эквиваленция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся истинным тогда и только тогда, когда все простые высказывания, образующие составное высказывание, одновременно истинны или одновременно ложны.

Математическая запись данной операции для логических переменных A, В, С… будет иметь вид:

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

Логические операции

Логические операции Логические операции позволяют комбинировать выражения, возвращающие логические величины. Язык JavaScript поддерживает три логические операции.Операция логического И (&&) возвращает true, если только оба операнда истинны. Например, (1 2). При

Логические схемы

Логические схемы Рабочая версия PSpice содержит более сотни логических устройств, доступных в коммерческой версии программного обеспечения. Имеется большинство логических схем серии 7400, триггеры, счетчики и т.п. Полная распечатка логических устройств демонстрационной

Логические операции

Логические операции Для создания объектов более сложных, чем изначальные звезды, прямоугольники и эллипсы, мы можем использовать логические операции. Это гораздо проще, чем полноценная векторная графика, где мы будем создавать фигуры с нуля.Для выполнения логических

Логические И и ИЛИ

Логические И и ИЛИ Вы уже видели, что такое управляющие структуры и как их использовать. Для решения тех же задач есть еще два способа. Это логическое И — «&&» и логическое «ИЛИ» — « || ». Логическое И используется следующим образом:выражение_1&&выражение_2Сначала

Когда использовать логические переменные

Когда использовать логические переменные Переменные типа Boolean могут хранить только два значения: True (в числовом представлении это 1) или False (0). Используйте переменные типа Boolean, когда нужно выяснить, какое из двух альтернативных условий имеет место в данный момент.

Глава 16 Логические операции

Глава 16 Логические операции • Понятие логических операций• Использование логических операцийРаботая с выделением, с которым мы познакомились в прошлой главе, можно использовать логические операции – это позволит в некоторых случаях упростить создание выделения или

Резюме: логические операции и выражения

IV. Логические операции

Поразрядные логические операции

Поразрядные логические операции Четыре операции производят действия над данными, относящимися к классу целых, включая char. Они называются «поразрядными», потому что выполняются отдельно над каждым разрядом независимо от разряда, находящегося слепа или справа.

4. Null-значения и логические операции

Логические операции (Logical operations)

Логические операции (Logical operations) template ‹class T›struct logical_and: binary_function‹T, T, bool› < bool operator()(const T& x, const T& y) const >;template ‹class T›struct logical_or: binary_function‹T, T, bool› < bool operator()(const T& x, const T& y) const >;template ‹class T›struct logical_not: unary_function‹T, bool› < bool operator()(const T& x) const

Логические операции

Логические операции Логические операции выполняют над своими операндами логические функции И (&&) и ИЛИ (||). Операнды логических операций могут иметь целый, плавающий тип, либо быть указателями. Типы первого и второго операндов могут различаться. Сначала всегда

4.3. Операции сравнения и логические операции

Логические операции

Логические операции В XSLT имеются две логические операции — or и and. Эти операции бинарны, то есть каждая из них определена для двух операндов. Если операнды не являются булевыми значениями, они неявным образом приводятся к булевому типу.Семантика or и and очевидна — они

3.2.4 Побитовые логические операции

»» ««применяются к целым, то есть к объектам типа char, short, int, long и их unsigned аналогам, результаты тоже цлые.Одно из стандартных применений побитовых логических опраций – реализация маленького множества

Логические операции

Логические операции К логическим относятся бинарные операции and, or и xor, а также унарная операция not, имеющие операнды типа boolean и возвращающие значение типа boolean. Эти операции подчиняются стандартным правилам логики: a and b истинно только тогда, когда истинны a и b, a or b истинно

Источник

Урок №7 Логические переменные и цикл while

Теория

Практика

Домашнее задание

Логические переменные

Цикл while

Бесконечный цикл while

Подсчёт суммы цифр числа

I Логические переменные

Под логическими переменными подразумеваются переменные, которые могут иметь только два значения: правда и ложь. Данные переменные очень удобны и могут быть использованы в качестве индикаторов.

Например, необходимо осуществить проверку числа на предмет принадлежности тому или иному множеству. После данной проверки программа кладёт в логическую переменную одно из двух значений: правда и ложь, в зависимости от того, пройдена или не пройдена проверка данного числа. Затем, исходя из значения данного индикатора, будет выполнены те или иные действия.

Логические переменные в С/С++

Использование в циклах

Логические переменные очень удобно использовать в циклах в качестве условия, так как при проверке на истинность того или иного условия, например, цикл if отправляет это условие в соответствующий оператор, а затем, в зависимости от того, true или false вернул оператор, условие считается истинным или ложным соответственно.

Работая с логическими переменными напрямую позволяет выполнять проверку условий в циклах гораздо быстрее, потому что циклу if не нужно вызывать никакого оператора.

II Цикл while

При его запуске программа выведет в консоли:

То есть цикл будет выполнять команды из своего тела, пока переменная х больше числа 5. При этом в каждом проходе значение данной переменной уменьшается на единицу. Когда значение переменной становится равным 5, условие x > 5 перестаёт быть истинным и цикл while завершает свою работу.

Заметим, что если строгое неравенство в условии поменять на нестрогое, программа выведет в консоли:

Так как при значении переменной х = 5 условие x >= 5 всё ещё остаётся истинным, и цикл while завершает свою работу только тогда, когда значение х станет равным числу 4.

III Бесконечный цикл while

Рассмотрим следующий код:

При его запуске программа выведет в консоли:

Бесконечный цикл while обычно создают при помощи логических переменных:

IV Подсчёт суммы цифр числа

А вот цикл while справится с подсчётом суммы цифр на ура. Заметим, что команды взятия остатка при делении на 10 и делении на 10 в целых числах необходимо выполнять до тех пор, пока число не станет нулём. И таким образом получается явная конструкция с использованием цикла while :

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§ 18 Алгебра логики

Информатика. 10 класса. Босова Л.Л. Оглавление

§ 18. Алгебра логики

Из курса информатики основной школы вы знаете, что для компьютерных наук большое значение имеет математическая логика, а точнее, её часть, называемая алгеброй логики.

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.

Джордж Буль (1815-1864) — английский математик, основоположник алгебры логики. Дж. Буль изучал логику мышления математическими методами и разработал алгебраические методы решения традиционных логических задач. В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.

18.1. Логические высказывания и переменные

Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно.

Например, высказывание «Джордж Буль — основоположник алгебры логики» истинно, а высказывание «2 + 2 = 5» ложно.

Что вы можете сказать об истинности или ложности предложения «Данное высказывание — ложь»?

Из имеющихся высказываний можно строить новые высказывания. Для этого используются логические связки — слова и словосочетания «не», «и», «или», «если …, то», «тогда и только тогда» и др.

Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым).

Например, из двух простых высказываний «Алгебра логики является основой строения логических схем компьютеров» и «Алгебра логики служит математической основой решения сложных логических задач» можно получить составное высказывание «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач».

Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С). Так, если обозначить элементарное высказывание «Джордж Буль — основоположник алгебры логики» именем А, а элементарное высказывание «2 + 2 = 5» именем В, то составное высказывание «Джордж Буль — основоположник алгебры логики, и 2 + 2 = 5» можно записать как «А и В». Здесь А, В — логические переменные, «и» — логическая связка.

Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь».

Для логических значений «истина» и «ложь» могут использоваться следующие обозначения:

Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

18.2. Логические операции

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

Из курса информатики основной школы вам известны логические операции отрицание, конъюнкция и дизъюнкция. Их таблицы истинности представлены ниже.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны, называется конъюнкцией или логическим умножением.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, называется дизъюнкцией или логическим сложением.

Логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному, называется отрицанием или инверсией.

При построении отрицания простого высказывания:

• используется оборот «неверно, что» или к сказуемому добавляется частица «не»;
• в высказывании, содержащем слово «все», это слово заменяется на «некоторые» и наоборот.

Рассмотрим несколько новых логических операций.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией или логическим следованием.

Операция импликации обозначается символом → и задаётся следующей таблицей истинности:

В разговорной речи импликации соответствуют предложения, содержащие связку «если …, то». Эту связку мы используем тогда, когда хотим показать наличие причинно-следственной связи, иначе говоря, зависимость одного события от другого. Например, пусть некоторый человек сказал: «Если завтра будет хорошая погода, то я пойду гулять». Ясно, что человек окажется лжецом лишь в том случае, если погода действительно будет хорошей, а гулять он не пойдёт. Если же погода будет плохой, то, независимо от того, пойдёт он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.

Результат операции импликации, как и других логических операций, определяется истинностью или ложностью логических переменных, а не наличием причинно-следственных связей между высказываниями. Например, абсурдное с житейской точки зрения высказывание «Если 2 > 3, то существуют ведьмы» является истинным с точки зрения алгебры логики.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.

Строгая дизъюнкция обозначается символом ⊕ и задаётся следующей таблицей истинности:

В русском языке строгой (разделительной) дизъюнкции соответствует связка «либо». В отличие от обычной дизъюнкции (связка «или») в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдёт только одно событие.

Например, высказывая утверждение «На сегодняшнем матче Петя сидит на трибуне А либо на трибуне Б», мы считаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б, и что сидеть одновременно на двух трибунах Петя не может.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.

В логике эквиваленция обозначается символом и задаётся следующей таблицей истинности:

В разговорной речи для выражения взаимной обусловленности используется связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».

Рассмотрим высказывание «Денис пойдёт в бассейн тогда и только тогда, когда он выучит уроки».

Это высказывание истинно (договорённость соблюдается), если истинны оба элементарных высказывания («Денис пойдёт в бассейн», «Денис выучит уроки»). Высказывание истинно (договорённость не нарушается) и в том случае, если оба элементарных высказывания ложны («Денис не пойдёт в бассейн», «Денис не выучит уроки»). Если же одно из двух высказываний ложно («Денис пойдёт в бассейн, хотя и не выучит уроки», «Денис выучит уроки, но не пойдёт в бассейн»), то договорённость нарушается, и составное высказывание становится ложным.

А сейчас посмотрите внимательно на таблицы истинности строгой дизъюнкции и эквиваленции: если на некотором наборе логических переменных результатом строгой дизъюнкции является истина, то на этом же наборе результатом эквиваленции всегда будет ложь, и наоборот.

Можно сделать выводы:

• операция эквиваленции есть отрицание операции строгой дизъюнкции

• операция строгой дизъюнкции есть отрицание операции эквиваленции

На сегодняшний день в алгебре логики не существует унифицированной символики для обозначения логических операций. В таблице 4.1 представлены логические операции и их наиболее распространённые обозначения, используемые как в алгебре логики, так и в некоторых языках программирования. Здесь же приведены речевые обороты, соответствующие логическим операциям.

Таблица 4.1

Логические операции и их обозначения

Операция отрицания выполняется над одним операндом. Такие операции называются одноместными или унарными. Все остальные логические операции, представленные в таблице 4.1, выполняются над двумя операндами и называются двуместными или бинарными.

18.3. Логические выражения

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (О, 1), логических переменных, знаков логических операций и скобок.

Для логического выражения справедливо:

1) всякая логическая переменная, а также логические константы (О, 1) есть логическое выражение;
2) если А — логическое выражение, то и 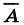— логическое выражение;
3) если А и В — выражения, то, связанные любой бинарной операцией, они также представляют собой логическое выражение.

При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:

1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.

Операции одного приоритета выполняются в порядке их следования, слева направо. Как и в арифметике, скобки меняют порядок выполнения операций.

Пример 1. Выясним, какие из приведённых слов удовлетворяют логическому условию (первая буква согласная → вторая буква согласная) & (последняя буква гласная → предпоследняя буква гласная):

1) ОЗОН;
2) ИГРА;
3) МАФИЯ;
4) ТРЕНАЖ.

Вычислим значение логического выражения для каждого из данных слов:

Итак, заданному условию удовлетворяют первое и четвёртое слова.

Решение логического уравнения — это один или несколько наборов значений логических переменных, при которых логическое уравнение становится истинным выражением.

Пример 2. Решим логическое уравнение

Дизъюнкция ложна в том и только в том случае, когда ложно каждое из образующих её высказываний. Иными словами, наше уравнение соответствует системе уравнений:

Таким образом, значение переменной D уже найдено. Импликация равна нулю в единственном случае — когда из истины следует ложь. Иначе говоря, в нашем случае: А = 1 и С = 0.

Подставим найденные значения переменных в уравнение

Ответ: А = 1, В = 1, С = 0, D = 0.

Логические уравнения могут иметь не одно, а несколько и даже очень много решений. Зачастую требуется, не выписывая все решения уравнения, указать их количество.

Пример 3. Выясним, сколько различных решений имеет логическое уравнение

Дизъюнкция истинна, если истинно хотя бы одно из образующих её высказываний. Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:

Первое равенство будет выполняться только при А = 1, В = 1 и С = 0. Поскольку D в этом уравнении не задействовано, оно может принимать любое из двух значений (0 или 1). Таким образом, всего первое уравнение имеет два решения.

Самостоятельно выясните, сколько решений имеет второе уравнение (из совокупности двух уравнений).

Сколько решений имеет исходное уравнение?

Пример 4. Выясним, сколько решений имеет очень простое с виду логическое уравнение х₁ & х₂ → х₃ & х₄ = 1.

Введём замену переменных. Пусть t₁ = х₁ & х₂, t₂ = х₃ & х₄. Тогда исходное уравнение примет вид: t₁ → t₂ = 1.

На t₁ никаких ограничений нет, эта переменная может принимать значения 0 и 1. Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t₁ и t₂ при которых t₁ → t₂ = 1.

Получаем для t₁ и t₂ три набора значений: 00, 01, 11. Первая двоичная цифра в каждом из этих трёх наборов — результат выражения х₁ & х₂, вторая — х₃ & х₄. Рассмотрим первый набор: существует три набора х₁ и х₂ таких, что х₁ & х₂ = 0, другими словами, первый 0 мы можем получить тремя способами. Второй О в этом наборе мы также можем получить тремя способами.

Из курсов информатики и математики основной школы вам известно одно из основных правил комбинаторики — правило умножения. Согласно ему, если элемент А можно выбрать n способами, и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами.

Согласно правилу умножения, пару 00 можно получить 3 • 3 = 9 способами.

Что касается пары 01, то первый 0 мы можем получить тремя способами, а для получения 1 существует единственный вариант (х₃ & х₄ = 1 при х₃ = 1 и х₄ = 1). Следовательно, есть ещё три набора переменных х₁, х₂, х₃, х₄, являющихся решением исходного уравнения.

Самостоятельно доведите решение этой задачи до конца.

18.4. Предикаты и их множества истинности

Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х 2 + у 2 = 1) — множество точек окружности единичного радиуса с центром в начале координат. Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами. Например, стандартное задание «Решить квадратное уравнение x 2 — 3x + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (x 2 — 3x + 2 = 0).

Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Пусть А и В соответственно являются множествами истинности предикатов А(х) и В(х). Тогда пересечение множеств А и В будет являться множеством истинности для предиката А(х) & В(х), а объединение множеств А и В будет множеством истинности для предиката А(х) ∨ В(х).

Пример 5. Найдём все целые числа 2, превращающие предикат

P(z) = (z > 5) & (z — 2 5) являются целые числа 6, 7, 8 и т. д. Множеством истинности предиката В(z) = (z — 2

Множество истинности исходного предиката — пересечение (общие элементы) множеств истинности образующих его предикатов:

Его мощность |Р| = 11.

Пример 6. Рассмотрим предикат (50 2 ) → (50 > (х + 1) 2 ), определённый на множестве целых чисел. Найдём множество истинности этого предиката.

Зачастую задания такого рода формулируют несколько иначе.

Например, так: «Найдите все целые числа х, для которых истинно высказывание (50 (х + 1)2)».

Проанализируем отдельно каждый из элементарных предикатов (50 2 ) и (50 > (x + 1) 2 ), решив соответствующие неравенства:

САМОЕ ГЛАВНОЕ

Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым). Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.

Логические операции имеют следующий приоритет:

1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.

Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.

Предикат — это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Вопросы и задания

1. Из данных предложений выберите те, которые являются высказываниями. Обоснуйте свой выбор.

1) Как пройти в библиотеку?
2) Коля спросил: «Который час?»
3) Картины Пикассо слишком абстрактны.
4) Компьютеры могут быть построены только на основе двоичной системы счисления.

2. Из каждых трёх выберите два высказывания, являющихся отрицаниями друг друга:

1) «1999 2000», «1999 ≤ 2000»;
2) «Петя решил все задания контрольной работы», «Петя не решил все задания контрольной работы», «Петя решил не все задания контрольной работы»;
3) «Луна — спутник Земли», «Неверно, что Луна — спутник Земли», «Неверно, что Луна не является спутником Земли »;
4) «Прямая а не параллельна прямой с», «Прямая а перпендикулярна прямой с», «Прямые а и с не пересекаются» (считаем, что прямые а и с лежат в одной плоскости);
5) «Мишень поражена первым выстрелом», «Мишень поражена не первым выстрелом», «Неверно, что мишень поражена не первым выстрелом».

3. Рассмотрите следующие элементарные высказывания: А = «Река Днепр впадает в Чёрное море», В = «45 — простое число», С = «Вена — столица Австрии», D = «0 — натуральное число».

Определите, какие из них истинные, а какие ложные. Составьте сложные высказывания, применяя каждый раз только одну из пяти логических операций

к высказываниям А, В, С и D. Сколько новых высказываний можно получить с помощью отрицания (инверсии)? Конъюнкции? Дизъюнкции? Импликации? Эквиваленции? Сколько всего новых высказываний можно получить? Сколько среди них будет истинных?

4. Представьте каждую пословицу в виде сложного логического высказывания, построенного на основе простых высказываний. Ответ обоснуйте при помощи таблиц истинности.

1) На вкус и цвет товарищей нет.
2) Если долго мучиться, что-нибудь получится.
3) Не зная броду, не суйся в воду.
4) Тяжело в ученье, легко в бою.
5) То не беда, что во ржи лебеда, то беда, что ни ржи, ни лебеды.
6) Где тонко, там и рвётся.
7) Или грудь в крестах, или голова в кустах.
8) За двумя зайцами погонишься — ни одного не поймаешь.
9) И волки сыты, и овцы целы.

5. Подберите вместо А, В, С, D такие высказывания, чтобы полученные сложные высказывания имели смысл:

1) если (А или В и С), то D;
2) если (не А и не В), то (С или D);
3) (А или В) тогда и только тогда, когда (С и не D).

7. Сколько из приведённых чисел Z удовлетворяют логическому условию: ((Z кратно 4) v (Z кратно 5)) → (Z кратно 6)?
1) 4; 2) 6; 3) 7; 4) 12.

8. Найдите все целые числа Z, для которых истинно высказывание:

9. Какие из высказываний А, В, С должны быть истинны и ка кие ложны, чтобы были ложны следующие высказывания?

10. Даны три числа в различных системах счисления:

Переведите А, В и С в двоичную систему счисления и вы полните поразрядно логические операции (A v В) & С. Отвеп дайте в десятичной системе счисления.

11. Логическое отрицание восьмиразрядного двоичного числа записанное в десятичной системе счисления, равно 217 Определите исходное число в десятичной системе счисления,

12. Определите логическое произведение и логическую сумм> всех двоичных чисел в диапазоне от 16₁₀ до 22₁₀, включая границы. Ответ запишите в восьмеричной системе счисления.

13. Сколько различных решений имеет логическое уравнение?

14. Сколько решений имеет логическое уравнение х₁ & х₂ v х₃ & x₄ = 1?

15. Изобразите в декартовой прямоугольной системе координат множества истинности для следующих предикатов:

16. Предикат ((8x — 6) 65) определён на множестве целых чисел. Найдите его множество истинности. Укажите наибольшее целое число х, при котором предикат превращается в ложное высказывание.

Источник