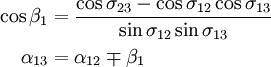Что такое линейная засечка

Линейная засечка.

Задача линейной засечки заключается в определении координат третьего пункта по координатам исходных пунктов и измеренным расстояниям от определяемого пункта до исходных (однократная засечка). Для контроля определения используются координаты третьего исходного пункта и расстояния до него от определяемого.

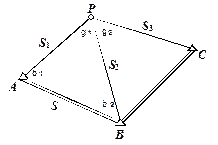Рис. 2.24.

Даны координаты пунктов А, B, C. Измерены линии S1, S2, S3. Требуется определить координаты точки P (X, Y). Рассмотрим однократную засечку с использованием пунктов А и В (рис. 2.24). 1. Решением обратной геодезической задачи определим дирекционный угол и длину линии АВ:

,

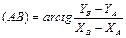
2. Определим угол β₁, используя теорему косинусов:

(43)

. (44)

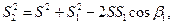
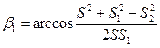
3. Определим дирекционный угол линии АР

(45)

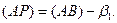
4. Определим координаты точки Р:

(46)

(47)

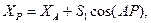
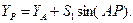
Для контроля решения задачи вычисляется длина линии ВР и сравнивается с измеренной

(48)

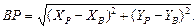
Расхождение не должно превышать 3 единиц последнего знака в измеренном значении линии S₂.

Для полного контроля определения вычисляется сторона СР и сравнивается с измеренной S₃

(48)

Источник

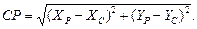
Основы геодезии

О геодезии и разный полезный материал для геодезистов.

Линейная засечка

Графическое решение. Проведем вокруг пункта A окружность радиусом S1 (в масштабе чертежа), а вокруг пункта B – окружность радиусом S2; точка пересечения окружностей является искомой точкой; задача имеет два решения, так как две окружности пересекаются в двух точках (рис.2.9).

Исходные данные: XA, YA, XB, YB,

Измеряемые элементы: S1, S2,

Неизвестные элементы: X, Y.

Аналитическое решение. Рассмотрим два алгоритма аналитического решения, один – для ручного счета (по способу треугольника) и один – для машинного счета.

Алгоритм ручного счета состоит из следующих действий:

1. решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
2. вычисление в треугольнике ABP углов β1 и β2 по теореме косинусов:
(2.29)
3. вычисление угла засечки γ
(2.30)
4. вычисление дирекционных углов сторон AP и BP:

пункт P справа от линии AB
(2.31)

пункт P слева от линии АВ
(2.32)
5. решение прямых геодезических задач из пункта A на пункт P и из пункта B на пункт P:

Результаты обоих решений должны совпадать.

Алгоритм машинного решения линейной засечки состоит из следующих действий:

1. решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
2. введение местной системы координат X’O’Y’ с началом в точке A и осью O’X’, направленной вдоль линии AB, и пересчет координат пунктов A и B из системы XOY в систему X’O’Y’:
(2.35)
3. запись уравнений окружностей в системе X’O’Y’:
(2.36)

и совместное решение этих уравнений, которое предусматривает раскрытие скобок во втором уравнении и вычитание второго уравнения из первого:
(2.37)

Если искомая точка находится слева от линии AB, то в формуле (2.39) берется знак “-“, если справа, то “+”.
4. пересчет координат X’ и Y’ точки P из системы X’O’Y’ в систему XOY по формулам (2.2):
(2.40)

Источник

Тема: Геодезические сети. Топографические съемки

_______ Для составления карт и планов, решения геодезических задач в том числе геодезического обеспечения строительства, на поверхности Земли располагают ряд точек, связанных между собой единой системой координат. Эти точки маркируют на поверхности Земли или в зданиях и сооружениях центрами (знаками).

_______ Геодезическая сеть – это система закрепленных точек земной поверхности, положение которых определено в общей для них системе геодезических координат.

_______ Геодезические сети подразделяют на плановые и высотные : первые служат для определения координат X и Y геодезических центров, вторые — для определения их высот.

_______ Принцип построения плановых геодезических сетей заключается в следующем. На местности выбирают точки, взаимное положение которых представляется в виде геометрических фигур: треугольников, четырехугольников, ломаных линий и т.д. Причем точки выбирают с таким расчетом, чтобы некоторые элементы фигур (стороны, углы) можно было бы непосредственно измерить, а все другие элементы вычислить по данным измерений. Например, в треугольнике достаточно измерить одну сторону и три угла (один для контроля правильности измерений) или две стороны и два угла (один для контроля правильности измерений), а остальные стороны и углы вычислить. Для вычисления плановых координат вершин выбранных точек необходимо кроме элементов геометрических фигур знать еще дирекционный угол стороны одной из фигур и координаты одной из вершин.

_______ Сети строят по принципу перехода от общего к частному, т. е. от сетей с большими расстояниями между пунктами и высокоточными измерениями к сетям с меньшими расстояниями и менее точным.

_______ Геодезические сети подразделяют на четыре вида: государственные, сгущения, съемочные и специальные. Государственные геодезические сети служат исходными для построения всех других видов сетей. Началом единого отсчета плановых координат в Российской Федерации служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге.

2. Методы создания геодезических сетей

_______ Плановые геодезические сети создаются методами триангуляции, полигонометрии и трилатерации. При построении геодезической сети методом триангуляции на местности закрепляется ряд точек, которые в своей совокупности образуют систему треугольников. В треугольниках измеряются все углы и некоторые стороны, которые называются базисными. По длине базисной стороны и измеренным углам, вычисляют длины всех сторон, а затем координаты всех пунктов сети.

_______ Метод полигонометрии заключается в построении на местности системы ломанных линий, называемых полигонометрическими ходами. Эти ходы прокладывают обычно между пунктами триангуляции. В полигонометрических ходах измеряются все углы поворота и длины всех сторон.

_______ При построении сети методом трилатерации на местности также строится сеть треугольников, в которых при помощи высокоточных дальномеров измеряются все стороны.

_______ Сети сгущения строят для дальнейшего увеличения плотности (числа пунктов, приходящихся на единицу площади) государственных сетей. Плановые сети сгущения подразделяют на 1-й.и 2-й разряды.

_______ Съемочные сети — это тоже сети сгущения, но с еще большей плотностью. С точек съемочных сетей производят непосредственно съемку предметов местности и рельефа для составления карт и планов различных масштабов.

_______ Специальные геодезические сети создают для геодезического обеспечения строительства сооружений. Плотность пунктов, схема построения и точность этих сетей зависят от специфических особенностей строительства.

_______ Государственные высотные геодезические сети создают для распространения по всей территории страны единой системы высот. За начало высот в Российской Федерации и некоторых других странах принят средний уровень Балтийского моря, определение которого проводилось в период с 1825 до 1840 г. Этот уровень отмечен горизонтальной чертой на медной металлической пластине, укрепленной в устое моста через обводной канал в Кронштадте.

_______ Между пунктами государственных высотных геодезических сетей высокой точности (1-го класса) размещают пункты высотных сетей низших классов (2-го, 3-го и т.д.). Несколько пересекающихся ходов называют сетями. Как правило, сети создают из ходов, прокладываемых между тремя или более точек. В целом точки (реперы) высотных сетей, называемых нивелирными, достаточно равномерно распределены на территории страны.

_______ На незастроенной территории расстояния между реперами составляют 5. 7 км, в го- родах сеть реперов в 10 раз плотнее

_______ Для решения ограниченного круга вопросов при изысканиях, строительстве и эксплуатации зданий и сооружений создают высотную сеть технического класса.

_______ Как правило, сети образуют полигоны с узловыми точками (общими точками пересечения двух или более ходов одного и того же класса). Каждый нивелирный ход опирается обоими концами на реперы ходов более высокого класса или узловые точки.

3. Закрепление на местности пунктов геодезических сетей

_______ Точки геодезических сетей закрепляют на местности знаками. По местоположению знаки бывают: грунтовые и стенные, заложенные в стены зданий и сооружений; металлические, железобетонные, деревянные, в виде откраски и т.д.; по назначению — постоянные, к которым относятся все знаки государственных геодезических сетей, и временные, устанавливаемые на период изысканий, строительства, реконструкции, наблюдений и т.д.

_______ Для того чтобы с одного знака был виден другой (смежный),над подземными центрами устанавливают наружные знаки в виде металлических или деревянных трех- или четырехгранных пирамид или сигналов.

_______ Как правило, пункты плановых разбивочных сетей и сетей сгущения закрепляют подземными центрами, такими же как и пункты государственных сетей. Так как расстояния между этими пунктами сравнительно небольшие, оформления их наружными знаками не требуется. Знаки могут закладывать в зданиях и сооружениях, в этом случае их называют стенными.

_______ Иногда для различных целей могут создаваться местные геодезические сети. Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей).

_______ Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами. Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ.

4. Топографические съемки, ее виды

_______ Существуют следующие виды топографических съемок:

_______ • теодолитная (горизонтальная),

_______ • мензульная и др.

4.1 Что такое теодолитная съемка

_______ Теодолитной съемкой называется горизонтальная или контурная съемка местности, которая выполняется с помощью теодолита.

_______ Для проектирования зданий, сооружений необходимо на район строительства иметь топографические материалы – планы, карты. При отсутствии таких материалов выполняют съемку данного участка местности.

4.2 Сущность теодолитной съемки

_______ Теодолитная съемка выполняется с помощью теодолита и рулетки (или дальномера соотвествующей точности). В результате теодолитной съемки получают контурный план местности.

_______ Съемку контуров выполняют на основе съемочных теодолитных ходов, которые прокладываются в виде :
а) замкнутых ходов,
б) разомкнутых ходов,
в) диагональных ходов.

_______ Теодолитная съемка складывается из следующих видов работ :
• прокладка теодолитных ходов и привязка их к пунктам геодезической сети,
• съемка ситуации,
• обработка результатов полевых измерений,
• построение плана.

5. Прокладка теодолитных ходов. Привязка к пунктам геодезической сети

_______ Привязка теодолитных ходов заключается в измерении привычных углов между сторонами теодолитного хода и геодезической сети, обязательно с контролем.

6. Съемка ситуации

_______ Съемка ситуации заключается в привязке контуров и предметов местности к сторонам и вершинам теодолитного хода.

6.1. Способ прямоугольных координат (способ перпендикуляров)

6.2. Способ полярных координат (полярный способ)

6.3. Способ линейных засечек

_______ Треугольники стараются делать близкими к равносторонним. Линейная засечка применяется часто при съемке строений. В этом случае расстояния измеряются лентой или рулеткой.

6.4. Способ угловых засечек

_______ Способ угловых засечек применяется в тех случаях, когда определить положение точки при помощи линейных измерений не удается.

6.5. Способ створов

_______ Абрис – это схематический чертеж, составленный в произвольном масштабе.

_______ На абрисе зарисовывается снимаемая ситуация и записываются результаты выполняемых при съемке угловых и линейных измерений. Абрис составляется отдельно на каждую сторону теодолитного хода. На основе абриса производится нанесение контуров местности на план.

Источник

Определение координат засечками.

Для определения планового положения точки необходимо измерить два элемента. Для контроля, кроме необходимых, выполняют избыточные измерения. Засечки различают прямые, обратные и комбинированные. В прямой засечке измерения выполняют на исходных пунктах (рис. 6.6 a, г); в обратной – на определяемом пункте (рис. 6.6 б, д); в комбинированной – на исходных и определяемом пунктах (рис. 6.6 в). В зависимости от вида измерений засечки бывают угловые (рис. 6.6 a, б, в), линейные (рис. 6.6 г), линейно-угловые (рис. 6.6 д). Измеренные углы на рис. 6.6 отмечены дугами, измеренные расстояния – двумя штрихами.

Рассмотрим вычисление координат в некоторых засечках.

Прямая угловая засечка. На исходных пунктах A и B с координатами , , , . (рис. 6.6 а) измеряют углы и . При обработке измерений сначала вычисляют дирекционные углы направлений AP и BP:

; .

Дирекционные углы с координатами связаны формулами обратной геодезической задачи

; .

Решая эти уравнения относительно x_p и y_p, получим формулы, по которым вычисляют координаты определяемой точки Р (формулы Гаусса):

; (6.5)

.

Для контроля ординату y_P вычисляют вторично по формуле:

.

Рис. 6.6. Схемы засечек: а – прямая угловая; б – обратная угловая; в – комбинированная угловая; г – линейная; д – линейно-угловая

Если один из дирекционных углов или близок к или , то вместо формул (6.5 – 6.7) вычисления выполняют по формулам

;

.

Для контроля аналогичные измерения и вычисления выполняют, опираясь на другую исходную сторону BC. За окончательные значения координат определяемой точки принимают средние.

Существуют и иные формулы решения прямой угловой засечки, например, формулы котангенсов углов треугольника (формулы Юнга):

; .

; .

Для контроля измеряют избыточный угол и вычисляют координаты, используя другую пару измеренных углов.

Для контроля измеряют избыточное расстояние d ₃ и вычисляют координаты из другого треугольника ВРС.

Источник

GIS-LAB

Географические информационные системы и дистанционное зондирование

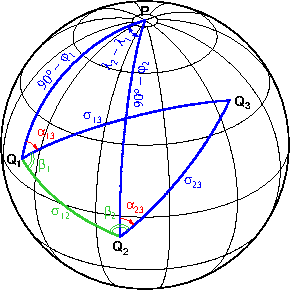
Задачи на сфере: линейная засечка

Линейная засечка — это нахождение положения точки по координатам двух исходных пунктов и расстояниям от этих пунктов до определяемой точки.

Содержание

[править] Общие положения

В качестве модели Земли принимается сфера с радиусом R, равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга.

Введём следующие обозначения:

Линейное расстояние по дуге большого круга s связано со сферическим расстоянием σ формулой s = R σ.

[править] Постановка задачи

[править] Алгоритм

Решение любого вида засечек сводится к нахождению полярных координат искомой точки, т.е. начального направления и расстояния на неё с одного из исходных пунктов. На конечном этапе координаты находятся из решения прямой геодезической задачи. Поскольку в линейной засечке расстояния σ₁₃ и σ₂₃ уже заданы, остаётся определить направление α₁₃ или α₂₃.

На рисунке синим цветом выделены заданные элементы сферических треугольников, красным цветом неизвестные, зелёным — вспомогательные элементы. Итак, в треугольнике Q₁Q₂Q₃ известны только два элемента — стороны σ₁₃ и σ₂₃. Из решения обратной геодезической задачи для пунктов Q₁, Q₂ можно получить недостающий третий элемент — расстояние σ₁₂, а также азимут α₁₂.

Угол β₁ и азимут α₁₃ вычисляются по формулам:

Если величина косинуса превышает единицу, задача поставлена некорректно, не выполняется закон «Длина стороны не может превышать сумму длин других сторон».

В общем случае имеется два решения, расположенных симметрично относительно большого круга Q₁Q₂. Следует явно определить, с какой стороны от направления Q₁Q₂ находится точка Q₃: если слева, как на рисунке, то в последней формуле ставим знак минус, если же справа — знак плюс.

[править] Пример программной реализации

Пример функции SphereLinear на языке Си, реализующей вышеизоложенный алгоритм:

Этот код находится в архиве Sph.zip в файле sph.c. Кроме того, в файл sph.h включены следующие определения:

Теперь напишем программу, которая обращается к функции SphereLinear для решения линейной засечки:

В архиве Sph.zip этот код находится в файле lin.c. Создадим исполняемый модуль lin компилятором gcc:

Впрочем, в архиве есть Makefile. Для MS Windows готовую программу lin.exe можно найти в архиве Sph-win32.zip.

Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и « [править] Ссылки

Последнее обновление: 2014-06-21 09:43

Дата создания: 11.03.2014
Автор(ы): ErnieBoyd

Источник