Что такое квантовая геометрия
Глава 10. Квантовая геометрия
Примерно за десятилетие Эйнштейн в одиночку сокрушил многовековые устои теории Ньютона, представив миру совершенно новую и значительно более глубокую теорию гравитации. И эксперты, и неспециалисты были покорены завораживающим изяществом и фундаментальной новизной формулировки общей теории относительности Эйнштейна. Не следует, однако, забывать о благоприятных исторических обстоятельствах, в значительной мере способствовавших успеху исследований Эйнштейна. Главное из них состоит в том, что Эйнштейну были известны математические результаты, полученные в XIX в. Георгом Бернгардом Риманом. Эти результаты давали возможность описания искривлённых пространств произвольной размерности в рамках строгого геометрического аппарата. В знаменитой инаугурационной лекции 1854 г. в Гёттингенском университете Риман перешёл через Рубикон мышления в рамках плоского евклидового пространства и проложил дорогу к единообразному математическому описанию геометрии всех типов искривлённых пространств. Именно пионерские идеи Римана позволили математикам дать количественное описание искривлённых пространств, подобных тем, которые иллюстрировались на рис. 3.4 и 3.6.
Гениальность Эйнштейна состояла в осознании того, что эти математические идеи были идеально приспособлены для выражения его новых взглядов на гравитационное взаимодействие. Он смело заявил о том, что математические понятия римановой геометрии безупречно согласуются с физикой гравитации.
В отличие от геометрии Римана, здесь нет готовых геометрических рецептов, уже описанных в книгах по математике и пригодных для того, чтобы занимающиеся струнами физики могли взять их на вооружение и использовать в этой науке. Напротив, современные физики и математики погружены в исследования в теории струн, по крупицам собирая знания, которые лягут в основу новой области физики и математики. И хотя основная часть работы ещё впереди, в ходе этих исследований уже было открыто много новых диктуемых теорией струн геометрических свойств пространства‑времени, которые наверняка произвели бы впечатление и на самого Эйнштейна.
Суть римановой геометрии
При прыжках на батуте его упругие волокна растягиваются под весом человеческого тела, и батут деформируется. Сильнее всего растяжение вблизи тела человека, а по мере приближения к краям батута растяжение менее заметно. Это наглядно видно, если на батут нанесено знакомое изображение (например, Мона Лиза). Если на батуте никто не стоит, изображение выглядит нормально, но если на батут встаёт человек, изображение искажается, в особенности непосредственно под человеком (см. рис. 10.1).
Рис. 10.1. Если на батуте с нанесённым изображением стоит человек, изображение сильнее всего искажается под весом тела человека
Этот пример иллюстрирует важнейший принцип описания искривлённых поверхностей, принятый в математической формулировке Римана. На основе более ранних наблюдений Карла Фридриха Гаусса, Николая Лобачевского, Яноша Бойяи и других математиков, Риман показал, что детальный анализ расстояний между всеми точками на поверхности объекта или внутри него даёт способ вычисления значения кривизны. Грубо говоря, чем больше (неоднородное) растяжение, тем сильнее отклонение от формулы для расстояний в плоском случае, и тем больше кривизна объекта. Например, батут сильнее всего растягивается под ногами человека, и поэтому расстояния между точками в этой области будут сильнее всего отличаться от расстояний в случае ненагруженного батута. Следовательно, кривизна батута здесь будет максимальной. Это интуитивно ясно из приведённого рисунка: именно в таких точках изображение на батуте искажено сильнее всего.
Такое наблюдение несущественно для стандартных приложений общей теории относительности к изучению макросистем. Например, проводя исследования в области космологии, физики, не задумываясь, рассматривают огромные галактики в качестве точек, так как размер галактик пренебрежимо мал по сравнению с размером Вселенной. Этот грубый подход к формулировке римановой геометрии оказывается, тем не менее, исключительно точным – в области космологии успех общей теории относительности очевиден. Однако в ультрамикроскопической области в силу протяжённых свойств струн риманова геометрия просто не является подходящим математическим формализмом. Как мы увидим ниже, она должна быть заменена квантовой геометрией теории струн, и эта замена приведёт к возникновению поразительных и неожиданных новых эффектов.
Космологическая сцена
Согласно космологической модели Большого взрыва вся Вселенная образовалась в результате необычайного космического взрыва, произошедшего около 15 миллиардов лет назад. Как впервые обнаружено Хабблом, даже сегодня продолжают разлетаться «осколки» этого взрыва, представляющие собой миллиарды галактик. Вселенная расширяется. Нам неизвестно, продолжится ли это расширение бесконечно, или в какой‑то момент расширение замедлится, затем прекратится, сменится сжатием, и, наконец, вновь приведёт к космическому взрыву. Астрономы и астрофизики пытаются изучить этот вопрос экспериментально, так как ответ зависит от величины, которую, в принципе, можно измерить, а именно от средней плотности материи во Вселенной.
Тщательно исследуя распределение галактик в пространстве, астрономы могут довольно точно предсказать среднюю плотность видимой материи во Вселенной. Она оказывается гораздо меньше критической. Однако имеются серьёзные основания полагать (как с теоретической, так и экспериментальной точки зрения), что Вселенная пронизана тёмной материей. Эта материя не участвует в ядерном синтезе, происходящем в звёздах, и поэтому не излучает свет. Следовательно, её нельзя обнаружить с помощью телескопа. Никому ещё не удавалось выяснить природу тёмной материи, не говоря уже о том, чтобы вычислить её точное количество. А это означает, что будущее нашей Вселенной, которая в настоящий момент расширяется, остаётся неясным.
Однако мы хорошо знаем, что если характерные длины приближаются к планковской или становятся меньше неё, уравнения общей теории относительности теряют свою силу ввиду квантово‑механических эффектов. На таких масштабах длин нужно использовать теорию струн. В результате встаёт вопрос о том, к каким изменениям геометрической картины на основе общей теории относительности, в которой допустим сколь угодно малый размер Вселенной (так же, как в римановой геометрии допустим сколь угодно малый размер абстрактного многообразия), приведёт использование теории струн. Вскоре мы увидим, что и здесь в теории струн имеются указания на ограничение физически достижимых масштабов длин, а новым замечательным следствием является невозможность сжатия Вселенной по любому пространственному измерению до размеров, меньших планковской длины.
Знакомство с теорией струн может вызвать у вас искушение высказать догадку, почему это так. Вы можете рассуждать, что независимо от того, сколько точек (имеются в виду точечные частицы) вы нагромождаете друг на друга, их суммарный объём остаётся равным нулю. Наоборот, если частицы – это струны, сжимающиеся при совершенно случайной ориентации, они заполнят шарик ненулевого размера, типа шарика планковских размеров, состоящего из спутанных резиновых лент. Такие соображения действительно не лишены смысла, но они не учитывают важные и тонкие свойства, изящно используемые в теории струн для обоснования минимального размера Вселенной. Эти свойства позволяют реально понять новую струнную физику и её влияние на геометрию пространства‑времени.
Чтобы пояснить эти важные стороны теории, рассмотрим сначала пример, в котором отброшены детали, несущественные для понимания новой физики. Вместо теории струн со всеми десятью пространственно‑временными измерениями или знакомой нам Вселенной с четырьмя протяжёнными измерениями снова рассмотрим вселенную Садового шланга. Эта вселенная, имеющая два пространственных измерения, была введена в главе 8 до обсуждения теории струн с целью разъяснения идей Калуцы и Клейна 1920‑х гг. Давайте использовать её в качестве «космологической сцены» для исследования теории струн в простой постановке. Достигнутое понимание свойств этой теории будет использовано ниже для того, чтобы лучше разобраться со всеми пространственными измерениями в теории струн. С этой целью вообразим, что сначала циклическое измерение вселенной Садового шланга имеет нормальный размер, но затем начинает сжиматься всё сильнее и сильнее, приближаясь по форме к Линляндии и приводя к Большому сжатию в упрощённом и частичном варианте.
Интересующий нас вопрос состоит в том, будут ли геометрические и физические характеристики этого космического коллапса иметь свойства, позволяющие явно отличить Вселенную, основанную на струнах, от Вселенной, основанной на точечных частицах.
Существенно новая черта
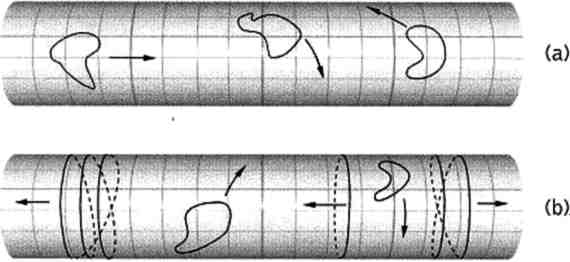
Не нужно много времени, чтобы обнаружить существенно новую характеристику физики струн. В нашей двумерной вселенной точечная частица может двигаться так, как показано на рис. 10.2: вдоль протяжённого измерения Садового шланга, вдоль циклического измерения, или по обоим измерениям сразу.
Рис. 10.2. Точечные частицы, движущиеся по цилиндру
Замкнутая струна может совершать аналогичные движения, с той разницей, что при движении по поверхности струна колеблется (рис. 10.3а ).
Рис. 10.3. Струны на цилиндре могут двигаться в двух конфигурациях – «ненамотанной» или «намотанной»
Это различие уже обсуждалось выше. Вследствие колебаний струна приобретает определённые характеристики, например массу и заряд. Это один из ключевых фактов теории струн, но он не является предметом настоящего обсуждения, так как его физические следствия уже рассмотрены выше.
Сейчас нас интересует другое отличие между движением частиц и струн, непосредственно связанное с формой пространства, где движется струна. Так как струна является протяжённым объектом, она может существовать ещё в одной конфигурации, отличной от упомянутых выше. Струна может наматываться (как лассо) на циклическое измерение вселенной Садового шланга (рис. 10.3б ). <67>Струна будет продолжать скользить и колебаться, но находясь в этой расширенной конфигурации. На самом деле, струна может намотаться на циклическое измерение любое число раз (как показано на том же рисунке) и одновременно осуществлять колебательные движения в ходе своего скольжения. Если струна имеет подобную намотанную конфигурацию, мы говорим, что она находится в топологической моде движения. Ясно, что топологическая мода может существовать только у струн. У точечных частиц не существует аналога этой моды. Попытаемся понять влияние этого качественно нового типа движения струны как на свойства самой струны, так и на геометрические свойства измерения, вокруг которого она намотана.
Глава 10. Квантовая геометрия
Примерно за десятилетие Эйнштейн в одиночку сокрушил многовековые устои теории Ньютона, представив миру совершенно новую и значительно более глубокую теорию гравитации. И эксперты, и неспециалисты были покорены завораживающим изяществом и фундаментальной новизной формулировки общей теории относительности Эйнштейна. Не следует, однако, забывать о благоприятных исторических обстоятельствах, в значительной мере способствовавших успеху исследований Эйнштейна. Главное из них состоит в том, что Эйнштейну были известны математические результаты, полученные в XIX в. Георгом Бернгардом Риманом. Эти результаты давали возможность описания искривлённых пространств произвольной размерности в рамках строгого геометрического аппарата. В знаменитой инаугурационной лекции 1854 г. в Гёттингенском университете Риман перешёл через Рубикон мышления в рамках плоского евклидового пространства и проложил дорогу к единообразному математическому описанию геометрии всех типов искривлённых пространств. Именно пионерские идеи Римана позволили математикам дать количественное описание искривлённых пространств, подобных тем, которые иллюстрировались на рис. 3.4 и 3.6.
Гениальность Эйнштейна состояла в осознании того, что эти математические идеи были идеально приспособлены для выражения его новых взглядов на гравитационное взаимодействие. Он смело заявил о том, что математические понятия римановой геометрии безупречно согласуются с физикой гравитации.
Но сейчас, почти век спустя после научного подвига Эйнштейна, теория струн даёт нам квантово-механическое описание гравитации, требующее пересмотра общей теории относительности на длинах порядка планковской. А так как в основе общей теории относительности лежит понятие римановой геометрии, то и само это понятие должно быть модифицировано для соответствия новой физике, возникающей на малых расстояниях в теории струн. И если в общей теории относительности постулируется, что свойства искривлённого пространства Вселенной описываются геометрией Римана, то в теории струн утверждается, что данный постулат справедлив лишь в случае, когда структура Вселенной рассматривается на достаточно больших масштабах. На длинах порядка планковской должна вступать в игру новая геометрия, согласующаяся с новой физикой теории струн. Эту новую геометрию называют квантовой геометрией.
В отличие от геометрии Римана, здесь нет готовых геометрических рецептов, уже описанных в книгах по математике и пригодных для того, чтобы занимающиеся струнами физики могли взять их на вооружение и использовать в этой науке. Напротив, современные физики и математики погружены в исследования в теории струн, по крупицам собирая знания, которые лягут в основу новой области физики и математики. И хотя основная часть работы ещё впереди, в ходе этих исследований уже было открыто много новых диктуемых теорией струн геометрических свойств пространства-времени, которые наверняка произвели бы впечатление и на самого Эйнштейна.
Квантовая геометрия: большой секрет
Физики всегда искали упущенную связь, которая могла бы объединить очень большое с очень маленьким. Сейчас при наличии явных и очевидных геометрических паттернов в Земле, весьма вероятно следующее: если мы действительно имеем дело с моделью единого поля, тогда паттерны, которые мы видим в большем масштабе, должны также появляться в квантовой механике. Атомы, чем быть пучком кажущихся твердыми частиц, вращающихся вокруг ядра, сейчас можно было бы представлять как геометрические паттерны потока внутри жидкообразной энергии Поля Источника. Когда вы увеличиваете частоту вибрации, геометрия усложняется. Как только мы начинаем понимать, как реально работает этот принцип, мы приходим к преобразованию элементов – классической мечте алхимиков о преобразовании свинца в золото.
“Очевидно, еще многое предстоит сделать в сфере расширения применения Теории Обратной Связи к внутренней структуре атома. Возможно, пора найти новый путь к исследованию механики Региона Времени. Поиск нового пути включает свежее мышление и переворачивание всех камней”.[656]
Первым ученым, которого я нашел, и у которого имелась работающая модель квантовой физики, основанная исключительно на геометрии, был Род Джонсон. Он разместил интригующие концепции на дискуссионном форуме Ричарда Хоагленда еще в 1996 году. В последующие годы я много раз брал у него интервью и публиковал результаты на своем сайте www.divinecosmos.com; к сожалению, он умер в 2010 году. Меня потрясло, сколь много загадок квантовой механики он мог объяснить с помощью геометрии, включая постоянную Планка, постоянную тонкой структуры, соотношение между сильным и слабым взаимодействием, структуру фотона и многое другое.[657] Не зная ничего о модели Ларсона, Джонсон независимо разработал аналогичную концепцию. Согласно модели Джонсона, существует параллельная реальность, которая непрерывно пересекается с нашей реальностью в каждом атоме, на самом крошечном уровне. Каждый атом обладает одной геометрией в нашей реальности и противоположной, обратной геометрией в параллельной реальности. Две геометрии вращаются в противоположных направлениях внутри друг друга. Каждая стадия этого процесса проводит вас через разные элементы. Ясно, что у Джонсона была великая модель, хотя и не имелось достаточно специфики для пересмотра всей Периодической Таблицы. Но он считал, что все ответы можно найти в теории цирклонов Джеймса Картера.[658]
Позже я нашел д-ра Роберта Муна, который мог объяснить все в Периодической Таблице посредством геометрии. Он был одним из ключевых ученых, вовлеченных в Манхэттенский Проект. Проект занимался разработкой первой в мире контролируемой реакции термоядерного расщепления. Мун был вторым из ученых, работавших над созданием циклотрона в 1930-х годах. Он значительно улучшил первый циклотрон, построенный Э. О. Лоуренсом. В Манхэттенском Проекте д-р Мун решал важные проблемы, связанные с первым ядерным реактором. После Второй мировой войны он создал первый микроскоп, сканирующий рентгеновские лучи. С 1974 года и до самой смерти в 1989 году он был ключевым сотрудником Линдона Х. Ларуша младшего.[659] На сайте Ларуша Наука и Технология 21-го Века можно найти разнообразные статьи Муна о новой модели квантовой физики.[660]
Возможно, вы заметили, что д-р Мун не включил в группирование тетраэдр. Он считает, что поскольку геометрической противоположностью тетраэдра является тетраэдр, он играет другую роль. И действительно, согласно модели Рода Джонсона и ранней модели Бакминстера Фуллера, фотон возникает в виде двух соединенных тетраэдров. И у нас есть надежные данные, подтверждающие это в постоянной Планка.[663]
В любом случае, когда мы пользуемся моделью Муна, происходят очень забавные вещи. Первой завершенной оболочкой в ядре является куб с восемью протонами. Это соответствует кислороду, который высоко стабилен. Он составляет 62,55% всех атомов в земной коре. Также интересно, что кислород является единственным самым важным элементом для поддержания жизни. Второй завершеной оболочкой является октаэдр с четырнадцатью протонами, на этот раз у нас есть кремний, составляющий 21,22%. И хотя мы считаемся углеродными жизненными формами, кремний тоже очень важен для биологической жизни. Представляется, он – ключевой ингредиент в экспериментах д-ра Игнасио Пачеко по спонтанному возникновению жизни (работа с кремнием, содержащимся в песке с побережья).
Д-р Роберт Мун открыл, что протоны атомов естественно собираются в Платоновы Твердые Тела, как видно здесь. Каждый протон соответствует вершине геометрии.
Итак, с одними первыми двумя оболочками – кислородом с кубическим ядром и кремнием с ядром в форме октаэдра – у вас есть 84% всех атомов в земной коре. Затем, когда вы движетесь к завершению следующей формы, икосаэдру, у вас есть 26 протонов. Это атом железа – самого лучшего металла для создания естественно возникающих магнитных полей. Именно эта скрытая геометрическая симметрия отвечает за магнитные свойства железа, действуя как канал для Поля Источника, что мы еще будем обсуждать. Из всех атомов в земной коре железо составляет 1,2%, но атомы железа составляют около 5% общего веса. Затем идет додекаэдр с 46 протонами. Сейчас у вас есть палладий – необычно симметричный атом, который используется во всех экспериментах холодного синтеза. И если вы думаете, что холодный синтез – это простая трата времени, не забывайте, что д-ра Юджина Мэллоува уволили с поста главного редактора технического бюллетеня МТИ после того, как он, предположительно, обнаружил, что они фальсифицируют данные о холодном синтезе, настаивая на отсутствии результатов.[664]
Согласно статье Лоренса Хечта, модель Муна удовлетворяет всем видам квантовых головоломок, включая процессы расщепления и синтеза, загадочный период 14 для редкоземельных элементов, точное количество элементов в каждом ряду Периодической Таблицы, магические числа Марии Гепперт-Майер, в которых свойства ядра имеют тенденцию вдруг меняться при определенных числах, любопытно появляющихся снова и снова, смотрите ли вы на протоны, нейтроны или массовое число.[665] Хечт продолжал развивать и обогащать модель Муна после смерти последнего в 1989 году.[666]
В теоретическая физика, квантовая геометрия набор математических понятий, обобщающих понятия геометрия понимание которых необходимо для описания физических явлений на масштабах расстояний, сравнимых с Планковская длина. На этих расстояниях квантовая механика оказывает глубокое влияние на физические явления.
Содержание
Квантовая гравитация
В альтернативном подходе к квантовой гравитации под названием петля квантовой гравитации (LQG) фраза «квантовая геометрия» обычно относится к формализм в LQG, где наблюдаемые, которые захватывают информацию о геометрии, теперь являются четко определенными операторами на Гильбертово пространство. В частности, некоторые физические наблюдаемые, например площадь, имеют дискретный спектр. Также было показано, что петлевая квантовая геометрия некоммутативный. [2]
Возможно (но считается маловероятным), что это строго квантованное понимание геометрии будет согласовываться с квантовой картиной геометрии, вытекающей из теории струн.
Квантовые состояния как дифференциальные формы
Интеграл перекрытия определяется как:
mathrm
в дифференциальной форме это
mathrm
Вероятность найти частицу в некоторой области космоса р дается интегралом по этой области:
mathrm
при условии, что волновая функция нормализованный. Когда р это все трехмерное позиционное пространство, интеграл должен быть 1 если частица существует.
Может ли квантовая механика объяснить существование пространства-времени?
Квантовая механика странная. Для нас, существ, не способных видеть микромир не вооруженным глазом, представить себе как все устроено на уровне атомов довольно сложно. Между тем, согласно атомной теории, все во Вселенной состоит из мельчайших частиц – атомов, скрепленных друг с другом электрическими и ядерными силами. Физические эксперименты, проведенные в ХХ веке показали, что атомы можно дробить на еще более мелкие, субатомные частицы. В 1911 году британский физик Эрнест Резерфорд провел ряд экспериментов и пришел к выводу, что атом похож на Солнечную систему, только по орбитам вместо планет вокруг него вращаются электроны. Два года спустя, взяв за основу модель Резерфорда, физик Нильс Бор изобрел первую квантовую теорию атома и в этой области теоретической физики все стало еще сложнее. Но если квантовая механика объясняет как взаимодействуют между собой мельчайшие частицы, может ли она объяснить существование пространства-времени?
Ученые ищут ответ на вопрос о том из чего состоит пространство-время уже много лет, но пока безуспешно
Что такое пространство-время?
Уверена, большинство из нас воспринимают пространственно-временной континуум как нечто, само собой разумеющееся. И в этом нет ничего удивительного, ведь не каждый день мы размышляем над чем-то подобным. Но если хорошенько задуматься, то окажется, что ответить на вопрос о том, что представляет собой пространство-время не так уж просто.
Начнем с того, что в соотвествии с теорией относительности (ОТО) Эйнштейна, Вселенная имеет три пространственных измерения и одно временное измерение. При этом все четыре измерения органически связаны в единое целое, являясь почти равноправными и в определенных рамках и условиях способными переходить друг в друга. В свою очередь пространственно-временной континуум или пространство-время – это физическая модель, дополняющая пространство временным измерением.
В рамках общей теории относительности пространство-время также имеет единую динамическую природу, а его взаимодействие со всеми остальными физическими объектами и есть гравитация.
В рамках ОТО теория гравитации и есть теория пространства-времени, которое не является плоским и способно менять свою кривизну.
Из ОТО также следует, что гравитация является результатом массы, такой как планета или звезда, искажающая геометрию пространства-времени. Космический аппарат NASA Gravity Probe, запущенный в 2004 году, точно измерил, насколько гравитация Земли искривляет пространство-время вокруг нее, в конечном итоге подтвердив расчеты Эйнштейна. Но откуда взялось пространство-время? Ответ, как это ни странно, может скрывать в себе квантовая механика.
Квантовая механика и теория гравитации
Как пишет портал Astronomy.com, сегодня физики стоят на пороге революции, которая может привести к пересмотру всего что мы знаем о пространстве-времени и, возможно, к объяснению того, почему квантовая механика кажется такой странной.
«Пространство-время и гравитация должны в конечном итоге возникнуть из чего-то другого», – пишет физик Брайан Свингл из Университета Мэриленда в статье, опубликованной в журнале Annual Review of Condensed Matter Physics. Иначе трудно понять, как гравитация Эйнштейна и математика квантовой механики могут примирить их давнюю несовместимость.
Квантовая механика противоречит ОТО
Взгляд Эйнштейна на гравитацию как проявление геометрии пространства-времени был чрезвычайно успешным. Но то же самое относится и к квантовой механике, которая с безошибочной точностью описывает махинации материи и энергии на атомном уровне. Однако попытки найти математическое решение, которое совместило бы квантовую странность с геометрической гравитацией, наталкивались на серьезные технические и концептуальные препятствия.
Хотите всегда быть в курсе последних новостей из мира популярной науки и высоких технологий? Подписывайтесь на наш новостной канал в Google News чтобы не пропустить ничего интересного.
По крайней мере, так было долгое время при попытках понять обычное пространство-время. Возможный ответ пришел из теоретического изучения альтернативных геометрий пространства-времени, мыслимых в принципе, но обладающих необычными свойствами. Одна из таких альтернатив известна как антидеситтеровское пространство, которое имеет тенденцию сжиматься само по себе, а не расширяться, как это делает Вселенная. Для жизни, безусловно, это было бы не самое приятное место. Но как лаборатория для изучения теорий квантовой гравитации, оно может многое предложить и даже стать ключом к квантовым процессам, которые могут быть ответственны за создание пространства-времени.
Что такое антидеситтеровское пространство?
Исследования антидеситтеровское пространства предполагают, например, что математика, описывающая гравитацию (то есть геометрию пространства-времени), может быть эквивалентна математике квантовой физики в пространстве с одним меньшим измерением.
Представьте себе голограмму — плоскую двумерную поверхность, которая включает в себя трехмерное изображение. Подобным же образом, возможно, четырехмерная геометрия пространства-времени может быть закодирована в математике квантовой физики, работающей в трехмерном пространстве. Или, может быть, нужно больше измерений — а вот сколько измерений требуется, являются частью проблемы, которую нужно решить.
Квантовая запутанность – одна из сложнейших для понимания научных теорий
Во всяком случае, исследования в этом направлении открыли удивительную возможность: само пространство-время может быть порождено квантовой физикой, в частности загадочным явлением, известным как квантовая запутанность. Подробно о том, что представляет собой квантовая запутанность я рассказывала в этой статье.
Если попробовать объяснить более-менее простыми словами, то квантовая запутанность это сверхъестественная связь между частицами, разделенными огромными расстояниями. Испускаемые из общего источника, такие частицы остаются запутанными независимо от того, как далеко они друг от друга находятся. Если вы измерите свойство (например, спин) одной частицы, то узнаете, каким будет результат измерения спина другой частицы. Но до измерения эти свойства еще не определены, что противоречит здравому смыслу и подтверждается многими экспериментами. Кажется, что измерение в одном месте определяет, каким будет измерение в другом отдаленном месте.
Энергичные усилия нескольких физиков подарили миру теоретические доказательства того, что сети запутанных квантовых состояний плетут ткань пространства-времени. Эти квантовые состояния часто описываются как «кубиты» — биты квантовой информации. Запутанные кубиты создают сети с геометрией в пространстве с дополнительным измерением, выходящим за пределы числа измерений, в которых находятся кубиты. Таким образом, квантовую физику кубитов можно приравнять к геометрии пространства с дополнительным измерением.
Примечательно, что геометрия, созданная запутанными кубитами, может очень хорошо подчиняться уравнениям из общей теории относительности Эйнштейна, которые описывают движение под действием гравитации — по крайней мере, последние исследования указывают в этом направлении.
Подводя итог отмечу, что никто точно не знает, какие квантовые процессы в реальном мире ответственны за соткание ткани пространства-времени. Возможно, некоторые допущения, сделанные в уже имеющихся расчетах, окажутся ошибочными. Но вполне возможно, что физика стоит на пороге проникновения в основы природы глубже, чем когда-либо. В существование, содержащее ранее неизвестные измерения пространства и времени.