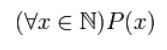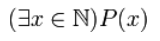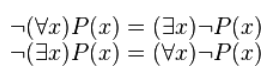Что такое кванторы в математике

Предикаты и кванторы

Вы будете перенаправлены на Автор24

Понятие предиката

Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Примеры предикатов

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

Готовые работы на аналогичную тему

Операции над предикатами

Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.

Кванторы

Чаще всего используют кванторы:

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов

С помощью квантора всеобщности можно записать следующие ложные высказывания:

который будет иметь вид:

Для записи истинных высказываний используем квантор существования:

Запись будет иметь вид:

Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами

Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

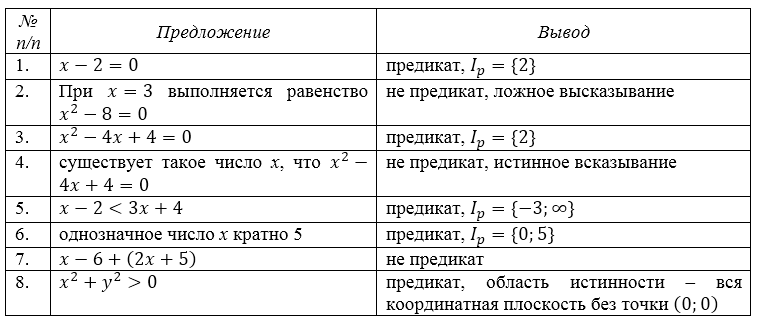
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата написания статьи: 07 04 2016

Источник

Кванторы

Наивное определение кванторов

Определить истинность или ложность подобных выражений при помощи таблиц истинности проблематично.

Когда кванторы не пререстановочны

Различные кванторы не перестановочны: «для любого \(x\) существует \(y\)» не тоже, что «некий \(y\) существует для любого \(x\)»: \[ \forall_x \, \exists_y\, A(x,y)

\exists_y\, \forall_x \, A(x,y). \] В обыденной жизни подобная неэквивалентность вполне естественна. Пусть \(A(x,y)\): «\(x\) имеет мать \(y\)». Тогда очевидно, что для «любого \(x\) существует мать \(y\)», тогда как утверждение «некая \(y\) является матерью всех людей \(x\)» истинно только в очень специфическом мире. Чтобы доказать не общезначимость формулы (т.е. что она не тавтология) достаточно придумать пример где она ложна.

\(\diamond\) Пусть предметная область — это натуральные числа: \(0,1. \), а предикат \(A(x,y):

Однотипные кванторы пререстановочны

Однотипные кванторы, можно переставлять местами: \[ \begin \forall_x\,\forall_y\,A(x,y) &

& \exists_y\,\exists_x\,A(x,y). \end \] В таких формулах иногда будет использоваться сокращение \(\forall_:

\forall_x\forall_y\) и аналогично для \(\exists\). Таким образом \(\forall_\equiv \forall_\) и \(\exists_\equiv \exists_\). Число аргументов предикатов, входящих в формулу, произвольно. Например, справедливо: \(\forall_x\,\forall_y\,A(w,x,v,y,z)

Другие свойства кванторов

Отрицание можно «проносить» через квантор, меняя его: \[ \begin \neg \forall_x\, A(x) &

& \exists_x\, \neg A(x),\\[2mm] \neg \exists_x\, A(x) &

& \forall_x\, \neg A(x). \end \] («если не верно для всех \(x\), то есть \(x\) для которого ложно»).

Действие любого квантора (\(\mathcal=\exists

\forall\)) можно расширять, вынося за дизъюнкцию или конъюнкцию (правила расширения действия): \[ \begin \mathcal_x\, A(x)

& \mathcal_x\, \bigr(A(x) \,\&\, B\bigr),\\[2mm] \mathcal_x\, A(x) \,\vee\, B &

& \mathcal_x\, \bigr(A(x) \vee B\bigr), \end \] где отсутствие явного указания у предиката \(B\) аргумента \(x\) означает, что он от \(x\) не зависит, а при отсутствии скобок приоритет кванторов считается максимальным, т.е. \(\forall_x A(x)\,\&\. \) — это \((\forall_x A(x))\,\&\. \) и т.д.

Наконец, для родственных операций (\(\&\) для \(\forall\) и \(\vee\) для \(\exists\) ) можно объединять кванторы ( правила объединения): \[ \begin \forall_x\,\forall_y\, \bigr(A(x)\,\&\,B(y)\bigr) &

& \forall_x\, \bigr(A(x)\,\&\,B(x)\bigr),\\[2mm] \exists_x\,\exists_y\, \bigr(A(x)\vee B(y)\bigr) &

& \exists_x\, \bigr(A(x)\vee B(x)\bigr). \end \]

Полезны также тождества разбиения: \[ \begin \forall_x\,\forall_y\, A(x,y) &

\forall_x\forall_y\,\bigr(x\neq y \,\to\,A(x,y)\bigr),\\[2mm] \exists_x\,\exists_y\, A(x,y) &

Для конечных предметных областей все эти тождества несложно доказать при помощи алгебры логики, записав квантор всеобщности как цепочку логических И, а квантор существования как цепочку логических ИЛИ. Постулируется, что все эти тождества справедливы не только для конечных, но и для бесконечных множеств.

Доказательства

Перестановочность кванторов непосредственно следует из коммутативности \(A\,\&\,B\equiv B\,\&\,A\) и правил поглощения \(A\,\&\,A\equiv A\).

Тождества с отрицанием следуют из правил \(\neg(A\,\&\, B)

\neg A\vee \neg B\): \[ \neg \forall_x\, A(x)

\exists_x\, \neg A(x), \] где \(A_i=A(x_i)\). Также легко доказываются правила расширения для родственных операций. Например \(\forall_x\, A(x) \,\&\, B

\forall_x\, \bigr(A(x) \,\&\, B\bigr)\) это \[ (A_1\,\&\,A_2\,\&\. )\,\&\,B \equiv (A_1\,\&\,B)\,\&\,(A_2\,\&\,B)\,\&\. \] где учтена ассоциативность, коммутативность и поглощение \(B\,\&\,B\equiv B\). Для неродственных операций используется свойство дистрибутивности. Так \(\forall_x\, A(x) \vee B

\forall_x\, \bigr(A(x) \vee B\bigr)\) это \[ (A_1\,\&\,A_2\,\&\. )\vee B \equiv (A_1\vee B)\,\&\,(A_2\vee B)\,\&\. \] Чтобы обосновать правила объединения кванторов с родственными операциями, распишем в \(\forall_x\forall_y\, \bigr(A(x) \,\&\, B(y))\) сначала \(\forall_y\), а затем \(\forall_x\): \[ (A_1\&\,B_1)\,\&\,(A_1\&\,B_2)\,\&\,(A_1\&\,B_3)\,\&\. (A_2\,\&\,B_1)\,\&\,(A_2\&\,B_2)\,\&\,(A_2\,\&\,B_3)\,\&\. \] По свойству поглощения это: \((A_1\,\&\,B_1)\,\&\,(A_2\,\&\,B_2)\,\&\. \equiv \forall_x\,(A_x\,\&\,B_x)\). Аналогично доказываются тождества разбиения.

Число существований

Пусть в теории определён предикат равенства \(x=y\), позволяющий выяснять одинаковы ли две сущности \(x\) и \(y\). С его помощью можно детализировать количество существующих объектов. Например:

Не более одного объекта \(\<0,1\>\) обладает свойством \(A\): \[ \forall_\, [ A(x)\,\&\,A(y) \to x=y ]. \]

Один и только один объект \(\<1\>\) обладает свойством \(A\): \[ \exists_x\,A(x)

\forall_\, [ A(x)\,\&\,A(y) \to x=y ]. \] Последний вид существования в единственном экземпляре иногда обозначают при помощи квантора с восклицательным знаком: \(\exists^_\,A(x)\). Аналогично строятся формулы относительно двух сущностей:

По меньшей мере два объекта \( \<2,3. \>\) обладают свойством \(A\): \[ \exists_\, [ A(x)\,\&\,A(y) \,\&\, x\neq y ]. \]

Не более двух объектов \(\<0,1,2\>\) обладают свойством \(A\): \[ \forall_\, [ A(x)\,\&\,A(y)\,\&\,A(z)

y=z) ]. \] Объединение двух последних формул логическим «И» приведёт к фразе: «в точности два объекта обладают свойством \(A\)». Подобным образом можно говорить о трёх сущностях, и т.д.

Источник

Квантор

Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих выcказывание. Чаще всего упоминают:

В математической логике приписывание квантора к формуле называется связыванием или квантификацией.

В многозначных логиках также вводятся и другие кванторы, например, квантор плюральности (квантор Решера) (обозначается перевёрнутой M, читается «для большинства …»).

Содержание

Примеры

Обозначим предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные):

.

Следующие (уже истинные) высказывания используют квантор существования:

Их формальная запись:

.

Введение в понятие

Пусть на множестве простых чисел задан предикат : «Простое число нечётно». Подставим перед этим предикатом слово «любое». Получим ложное высказывание «любое простое число нечётно» (это высказывание ложно, так как 2 — простое чётное число).

Подставив перед данным предикатом слово «существует», получим истинное выcказывание «Существует простое число , являющееся нечётным» (например, ).

Таким образом, превратить предикат в высказывание можно, поставив перед предикатом слова («все», «существует» и другие), называемые в логике кванторами.

Кванторы в математической логике

(«При всех значениях (x) утверждение верно»).

(«Существует (x) при котором утверждение верно»).

Свободные и связанные переменные

Множество свободных переменных* формулы F определяется рекурсивно, следующим образом:

Связанное переименование, свободное переименование

Операции над кванторами

Правило отрицания кванторов — применяется для построения отрицаний высказываний, содержащих кванторы, и имеет вид:

История появления

Философы давно обращали внимание на логические операции, ограничивающие область истинности предиката, однако не выделяли их в отдельный класс операций. Так, Томас Гоббс считал, что они являются частями имен. [1]

Хотя кванторно-логические конструкции широко используются как в научной, так и в обыденной речи, их формализация произошла только в 1879 г., в книге Фреге «Исчисление понятий». Обозначения Фреге имели вид громоздких графических конструкций и не были приняты. Впоследствии было предложено множество более удачных символов, но общепринятыми стали обозначения для квантора существования (перевёрнутая первая буква англ. Exists — существует), предложенное Чарльзом Пирсом в 1885 г., и для квантора общности (англ. All — все), образованное Герхардом Генценом в 1935 г. по аналогии с символом квантора существования. Термины «квантор», «квантификация» также предложил Пирс.

Литература

Ссылки

Примечания

Полезное

Смотреть что такое «Квантор» в других словарях:

КВАНТОР — логический оператор, с помощью которого высказывание о к. л. отдельном объекте преобразуется в высказывание о совокупности (множестве) таких объектов. В логике используется два основных К.: К. общности, «V», и К. существования, «Э». В… … Философская энциклопедия

квантор — сущ., кол во синонимов: 1 • оператор (24) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

квантор — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN quantifier … Справочник технического переводчика

КВАНТОР — общее название для логических операций, к рые по предикату Р(х)строят высказывание, характеризующее область истинности предиката Р(х). В математич. логике наиболее употребительны квантор всеобщности и квантор существования Высказывание означает,… … Математическая энциклопедия

Квантор — (от лат. quantum сколько) символ, используемый для обозначения некоторых операций математической логики, одновременно логическая операция, дающая количественную характеристику области предметов, к которым относится выражение, получаемое в… … Начала современного естествознания

квантор — а, ч., лог. Логічний оператор, який переводить одну висловлювальну форму в іншу. Квантор існування … Український тлумачний словник

квантор — kvantorius statusas T sritis automatika atitikmenys: angl. quantifier vok. Quantor, m rus. квантор, m pranc. quantifier, m … Automatikos terminų žodynas

Квантор — (от лат. quantum сколько) логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа… … Большая советская энциклопедия

квантор — кв антор, а … Русский орфографический словарь

Источник

MT1102: Линейная алгебра (введение в математику)

В алгебре высказываний применяют логические знаки для записи различных утверждений. Однако нам не достаточно этих знаков для выражения мысли типа «Всякий элемент %%x%% из множества %%D%% обладает свойством %%P(x)%%».

Понятие кванторов

Введем новые логические знаки, обозначаемые %%\forall%%, %%\exists%% и %%\exists!%%. Знак %%\forall%% называется квантором всеобщности, знак %%\exists%% — квантором существования, а %%\exists!%% — квантором существования и единственности.

Пусть %%P(x)%% — одноместный предикат, определенный на множестве %%D%%.

Квантор всеобщности

Используя квантор всеобщности, можно составить следующее высказывание

Читается как: «для любого %%x%% выполняется %%P(x)%%»; «для всякого %%x

P(x)%%»; «для всякого %%x%% верно %%P(x)%%» и т.п.

Пусть %%P(x)%% предикат %%x^2 \geq 0%%, определенный на множестве действительных чисел %%D = \mathbb R %%. Тогда высказывание %%\forall x

P(x)%% имеет вид %%\forall x

x^2 \geq 0%%. Это истинное высказывание, так как для любого значения пременной %%x = a \in \mathbb R %% получаем истинное высказывание %%a^2 \geq 0%%. Однако, высказывание %%\forall x

x^2 > 0%% ложно, например, как при %%x = 0%% получаем ложное высказывание %%0 > 0%%.

Квантор существования

Используя квантор существования, можно составить следующее высказывание

Читается как: «существует %%x%% такой, что %%P(x)%%»; «существует %%x%% с условием %%P(x)%%» и т.п.

Квантор существования и единственности

Используя квантор существования и единственности, можно составить следующее высказывание

Читается как: «существует единственный %%x%% такой, что %%P(x)%%»; «существует единственный %%x%% с условием %%P(x)%%» и т.п.

Отрицание «кванторов»

Докажем первое из них. Пусть высказываине %%\overline<\forall x

P(x)>%% истинно. Тогда высказывание %%\forall x

P(x)%% ложно. Поэтому для некоторого %%x = a%% имеем %%P(a)%% ложно. Тогда %%\overline%% истинно. Итак, для некоторого значения %%x = a

\overline%% истинно. Поэтому высказывание %%\exists x

Аналогично доказывается второе утверждение.

Применение одного из кванторов «понижает» степень предиката на единицу. Из двуместного предиката получается одноместный предикат, а из одноместного — предикат %%0%% степени или высказывание.

Правила перестановки кванторов

P(x,y) \equiv \exists y

P(x,y) \equiv \forall y

Однако, разноименные кванторы переставлять местами нельзя. Рассмотрим двуместный предикат %%P(x, y): x + y = 0%%, определенный на множестве %%\mathbb R%%. Тогда высказывание %%\exists x

x + y = 0%% можно прочитать так: «существует %%x%%, которое в сумме с любым %%y%% равно 0». Это ложно высказывание.

Переставим разноименные кванторы местами и получим высказывание %%\forall y

x+ y = 0%%, которое можно прочитать так: «для любого %%y%% существует %%x%% такой, что их сумма равна 0». Это истинное высказывание. В итоге получили различные истинностные значения высказываний.

Для записи одноименных кванторов существуют следующие сокращения:

\forall y \equiv \forall x, y

\exists y \equiv \exists x, y. \end $$

Источник

Логика: предикатная, формальная и сентенциальная. Кванторы и возникновение информатики

1 | Введение

Логика, как эпистемологический инструмент, — исследующий знание как таковое, — изобретена независимо в трёх отдельных государствах: Греции (Аристотелем), Китае (до правления Цинь Шихуанди) и Индии. В последних двух государствах логика не распространилась настолько, чтобы получить полноценное развитие. В античной же Греции логика сформировалась в своих основах столь определённо, что дополнилась только через 2 тысячелетия.

Значительные изменения в греческую логику, помимо Буля, Моргана и Рассела, внёс Фреге — самая важная фигура основателей формальной семантики. Он разработал логику предикатов и 2 вида кванторов, попытавшись создать «логически совершенный язык» о котором мечтал Лейбниц. Значимой личностью является также Гёдель, который открыл знаменитые две теоремы о неполноте, описывающие невозможность объединения множества доказуемых утверждений со множеством истинных. Он утверждал, что доказательства математики зависят от начальных предположений, а не фундаментальной истины, из которой происходят ответы. Одна из главных идей его работ состоит в том, что ни один набор аксиом, — в том числе математических, — не способен доказать свою непротиворечивость.

На этом этапе некоторые заметят влияние платонизма на австрийского логика. Совершенно верно, ведь Гёдель не раз заявлял о влиянии метафизики Платона на собственную деятельность. Но сам Платон развитию формальной логики способствовал лишь косвенно: в истории он вносит вклад в развитие другого направления — философской логики. Платоном созданы вопросы, на которых основывается вся западная академическая философия вплоть до наших дней. Философия, в том виде, котором она известна, возникла только благодаря учителю Аристотеля.

Платон — учитель Аристотеля

В другие периоды в логику также вносили дополнения:

античной школой стоицизма введены термины «модальности», «материальной импликации», «оценки смысла и истины», которые являются задатками логики высказываний;

также средневековыми схоластами введены несколько понятий;

Но главное, что сами логические операции не изменились. «Органон» Аристотеля, как сборник из 6 книг — первоисточник, где подробно описаны главные логические законы. «Органон» (с древнегреческого ὄργανον), означает — инструмент. Аристотель считал, что логика является инструментом к познанию. Он объединяет методом получения информации такие науки:

Физика — наука о природе;

Метафизика — наука о природе природы;

Биология — раздел физики, наука о жизни;

Психология — раздел физики, наука о душе;

Кинематика — раздел физики, наука о движении;

2 | Терминология

У каждой из наук должен быть идентичный фундамент в способе получения гнозисов (знаний), который позволит упорядочить информацию и вывести новые силлогизмы (умозаключения). Только таким образом получится прогресс в познании истины. Без логики наука была бы похожа на коллекционирование фактов, ибо информация бы не поддавалась анализу.

Сам Аристотель находит логике как средству убеждения иное применение: в риторике, спорах, дебатах, выступлениях и т.д., описывая это в труде «Риторика». В западной философии принято давать чёткие определения перед рассуждениями, поэтому определимся с терминами. Логика — наука о правильном мышлении.

В языковой зависимости возникают трудности трактовки термина «наука», но даже в оригинальном названии труда Фридриха Гегеля «Наука логики» — «Wissenschaft der Logik», употребляется слово «наука» (Wissenschaft). Поэтому придём к консенсусу и будем считать, что научной можно назвать ту дисциплину, в которой возможны открытия, исследование и анализ. Логика в таком случае — наука, ибо внутри неё возможно совершать открытия. Яркий пример — комбинаторика Лейбница.

Слово «правильный» веет нормативными коннотациями: правильное поведение, правильное выражение лица, и т.д. Перечисленное соответствует некоторым критериям и логика выставляет их (критерии) для правильного мышления.

Слово «мышление» понимается на интуитивном уровне, но чёткое объяснение затруднительно, обширно и иногда не объективно.

Бюст Аристотеля

3 | Формальная и неформальная логика

Первоначально, деление логики происходит на формальную и неформальную. Формальная логика отличается тем, что, в отличие от неформальной, записывается уравнениями. Неформальная же логика пишется выражениями в форме языка, поэтому она подходит для риторики, а формальная логика для абстрактных наук.

Формальная логика равным образом делится на дедуктивную и индуктивную. Они различаются тем, что в дедуктивном аргументе истинность условий гарантирует истинность умозаключения или вывода. В индукции же, при истинности условий одинаково возможен ложный и истинный вывод.

Законы формальной логики:

1. Закон тождества (А = А): эквивокация или двусмысленность недопустимы. Нельзя подменять одно понятие, другим.

2. Закон непротиворечия (А ∧ ¬А = 0): одно и то же утверждение не может быть истинным и ложным одновременно.

3. Закон исключения третьего или бивалентности (А ∨ ¬А = 1): утверждение может быть либо истинным, либо ложным — третьего не дано.

Принципы формальной логики:

1. Принцип достаточного обоснования: достаточными являются такие фактические и теоретические обоснования, из которых данное суждение следует с логической необходимостью.

4 | Сентенциальная логика (алгебра высказываний)

Базовые операции сентенциальной логики — логики высказываний, где заглавная буква означает предложение:

Отрицание (Утверждение ¬A истинно тогда и только тогда, когда A ложно): если имеем утверждение «А» и имеем утверждение «не А», то, когда утверждение «А» будет истинным — утверждение «не А» будет ложным. Также и когда утверждение «А» будет ложным — утверждение «не А» будет истинным.

Конъюнкция (Утверждение A ∧ B истинно, если и A, и B — истинны. Ложно в противном случае): в английском языке — союз «and/&»; в русском — «и». В утверждении «А и В», между «А» с «В» стоит знак конъюнкции — «∧». Утверждение «А и В» является истинным, если «А» с «В» являются истинными одновременно. Если хоть один элемент ложен, то всё утверждение ложно. «А и В» подразумевает, во-первых: истинность «А», во-вторых: истинность «В».

Дизъюнкция (Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны — утверждение ложно): в английском языке — союз «or»; в русском — «или». Существует два типа дизъюнкции — включающая и исключающая (в логике используется включающее «или»). Условия таковы, что утверждение «А или В» будет истинным, когда один или оба элемента истинны, но никогда — когда оба элемента ложны. Это противоречит нашему обыденному мышлению, т.к. когда спрашивают: «Чай или кофе?» мы выбираем один элемент, но в логике подразумевается выбор не только одного, а нескольких возможных.

Импликация (Утверждение A ⇒ B ложно, только когда A истинно, а B ложно): в английском языке — «therefore»; в русском языке — «следовательно». Подразумевает истинность одного элемента при истинности другого. Потому что условия истинности соблюдаются всегда, кроме случая, когда «А» истинно, а «B» ложно. Поэтому утверждение: «А» ложно, следовательно «B» ложно — истинно. Покажется, что когда «А» ложно, а «В» истинно — не соблюдаются условия, но это не так. Если вы скажете, что после дождя промокните — это утверждение будет истинным вне зависимости от того, пошёл дождь или нет.

Эквивалентность (Утверждение A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны): если истинно утверждение «А, следовательно В» и истинно утверждение «В, следовательно А», то истинными являются выражения «А эквивалентно В» и соответственно «В эквивалентно А». Условия истинности соблюдаются в случаях, когда оба элемента истинны или оба ложны.

Значение переменных

5 | Предикатная логика первого порядка

В XX веке, после добавлений в область логики работ Лейбница и Фреге, на основе этой дисциплины создаётся новая — информатика. Программирование сохраняет преемственность с видоизменённой логикой Аристотеля — предикатной логикой, описательная способность которой выше, чем у логики высказываний (сентенциальной).

Прежде чем разобрать этот новый тип логики, поговорим об её отличии от сентенциальной. Главная особенность предикатной логики, что заглавными буквами обозначаются предикаты, а не целые высказывания. Можно сказать, что предикат — это математическая функция, которая «накладывает» множество субъектов на множество утверждений.

Высказывание «Я пошёл в зоопарк» — состоит из субъекта и предиката. В нём субъект — «Я», а предикат — то, что остаётся кроме субъекта («пошёл в зоопарк»). Субъект — тот, кто совершает действие в предложении или имеет выраженное свойство; предикат — всё оставшееся. Таким образом, если в сентенциальной логике высказывание «Я пошёл в зоопарк» выражалось бы одной заглавной буквой, то в логике предикатов использовались бы две буквы (заглавная и подстрочная): «P» — для предиката; «x» — для субъекта. Субъекты обозначаются переменной («x»), потому что в предикатной логике появляются две относительно новые операции: универсальный и экзистенциальный кванторы. Особенность кванторов заключается в том, что ими возможно записать выражение истинное при всех возможных переменных «х» или хотя бы при одном.

Универсальный квантор (квантор всеобщности) обозначается символом — «∀», с указанием переменной под ним. Возьмём утверждение «Все пингвины чёрно-белые». В логике высказываний оно бы выражалось как «X ⇒ P», где «X» — нечто являющееся пингвином, а «P» — нечто являющееся чёрно-белым. В предикатной логике же используются субъекты и предикаты, поэтому нечто являющееся пингвином (субъект), обозначалось бы переменной «х» снизу под предикатом. «»х» — является пингвином, следовательно, является чёрно-белым». Записывается так: P(х) ⇒ B(х), где P(х): х — пингвин; B(х): x — чёрно-белый.

Однако этого недостаточно, ведь непонятно, один субъект «х» чёрно-белый или больше одного, а может вообще все. Поэтому утверждение «»х» — является пингвином, следовательно, является чёрно-белым», берётся в скобки и перед скобками используется символ «∀» с переменной «х» под ним — которые вместе и будут универсальным квантором.

Универсальный квантор переводится как: «Для всех «х» истинно, что …». Теперь утверждение «х — является пингвином, следовательно, является чёрно-белым» с универсальным квантором перед ним, расшифровывается так: «Для всех «х» истинно, что «х» — является пингвином, следовательно, является чёрно-белым». Это означает, что чем бы ни был объект во вселенной, если этот объект пингвин — он является чёрно-белым. Полная запись будет выглядеть так:

Экзистенциальный квантор (квантор существования) обозначается символом — «∃» с указанием переменной под ним. Возьмём утверждение «Некоторые пингвины серые». Как и в прошлый раз, выражение «»x» — является пингвином и «х» — является серым» возносим в скобки и ставим перед ними квантор, в этом случае экзистенциальный с указанной переменной. «»x» — является пингвином и «х» — является серым» записывается так: P(х) ∧ C(х), где P(х): х — пингвин; C(х): x — серый.

Экзистенциальный квантор можно перевести так: «Есть такой «х», для которого будет истинно, что …». Подразумевается, что есть как минимум один «х», для которого выполняются условия выражения. Если вам говорят, что ДНК не существует, достаточно показать одну молекулу дезоксирибонуклеиновой кислоты для опровержения этого утверждения. Также и с кванторами, если существует хотя бы один серый пингвин, то утверждение об отсутствии серых пингвинов будет ложно. Полная запись экзистенциального квантора для выражения «Есть такой «х», для которого будет истинно, что «x» — является пингвином и «х» — является серым», будет выглядеть так:

6 | Заключение

Примечательно, что есть возможность перевода одного вида квантора в другой. Возьмём утверждение «Все пингвины не являются серыми». Для универсального квантора текстовая запись будет такая: «Для всех «х», будет истинным утверждение о том, что если «х» — является пингвином, то «х» — не является серым объектом». Но утверждение изменяется и для экзистенциального квантора, используя знак отрицания: «Нет такого «х», для которого бы было истинным утверждение о том, что «x»— является пингвином и «х»— является серым».

В середине XIX века, Готлоб Фреге дополнил логику Аристотеля двумя этими операциями, которые позже сформировались в отдельную дисциплину — предикатную логику. С введением в логику экзистенциального квантора (после универсального) — предикатная логика, в основе своей, завершилась как система…

Источники:

1 — Аристотель: «Органон» — «Первая аналитика» и «Вторая аналитика»;

2 — Аристотель: «Риторика»;

3 — Готлоб Фреге: «Исчисление понятий»;

4 — «Monatshefte für Mathematik und Physik» 1931 г.: Курт Гёдель «О принципиально неразрешимых положениях в системе Principia Mathematica и родственных ей системах»;

5 — The Early Mathematical Manuscripts of Leibniz;

6 — Мельников Сергей: «Введение в философию Аристотеля»;

7 — Гильмутдинова Нина: «Логика и теория аргументации»;

Источник