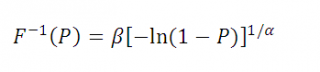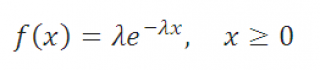Что такое квантиль порядка p

Квантиль

Материал из MachineLearning.

Содержание

Определение

—кванти́ль случайной величины с функцией распределения — это любое число удовлетворяющее двум условиям:

Заметим, что данные условия эквивалентны следующим:

и x_\alpha)\le 1- \alpha.» alt= «\mathbb

(\xi>x_\alpha)\le 1- \alpha.» />

Если — непрерывная строго монотонная функция, то существует единственный квантиль любого порядка который однозначно определяется из уравнения и, следовательно, выражается через функцию, обратную к функции распределения:

Кроме указанной ситуации, когда уравнение имеет единственное решение (которое и дает соответствующий квантиль), возможны также две других:

Часто используемые квантили специальных видов

Терминология, принятая в математической статистике

В задачах математической статистики часто возникает необходимость отделить сверху, снизу или с обеих сторон области, вероятности попадания в которые малы. В связи с этим часто используется следующая терминология.

Нижний (односторонний) квантиль уровня — то же, что и обычный квантиль порядка :

Верхний (односторонний) квантиль уровня — обычный квантиль порядка :

Применение квантилей в задачах проверки статистических гипотез

Если статистика с указанными свойствами существует, тогда на ее основе можно получить статистический критерий для данной задачи. Для этого необходимо с помощью соответствующих квантилей выделить область (нижнюю, верхнюю или двустороннюю), попадание в которую было бы маловероятно при нулевой гипотезе (и эта вероятность известна), однако может быть объяснено тем, что на самом деле имеет место альтернатива. Многочисленные критерии принятия решения строятся именно по такой схеме.

Применение квантилей в задачах оценивания параметров

Далее можно попробовать разрешить неравенство, стоящее под вероятностью, относительно неизвестного параметра, и переписать его в виде:

чтобы величины и зависели бы только от выборки, т.е. являлись бы статистиками. Если это удается сделать, то мы построили доверительный интервал для неизвестного параметра.

Выборочные квантили; статистическая оценка квантилей

Таким образом, выборочные квантили являются несмещёнными оценками обычных (не выборочных) квантилей.

Источник

Квантиль порядка р

1.11 Квантиль порядка р

Смотреть что такое «Квантиль порядка р» в других словарях:

квантиль — 3.32 квантиль (fractile): р квантиль (квантиль уровня р или процентиль) и соответствующее значение квантили хропределяется как: F(xp) = p, (3.1) где F функция распределения для хр. Источник … Словарь-справочник терминов нормативно-технической документации

КВАНТИЛЬ — величина, характеризующая функцию распределения F(x). К. распределения порядка р, 0 Геологическая энциклопедия

Квантиль — одна из числовых характеристик случайных величин, применяемая в математической статистике. Если функция распределения случайной величины Х непрерывна, то квантиль Kp порядка р определяется как такое число, для которого вероятность… … Большая советская энциклопедия

КВАНТИЛЬ — одна из числовых характеристик распределения вероятностей. Для действительной случайной величины Xс функцией распределения F(x)квантилью порядка р, 0 Математическая энциклопедия

ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… … Словарь-справочник терминов нормативно-технической документации

ГОСТ 15895-77: Статистические методы управления качеством продукции. Термины и определения — Терминология ГОСТ 15895 77: Статистические методы управления качеством продукции. Термины и определения оригинал документа: 2.30. k я порядковая статистика x(k) Определения термина из разных документов: k я порядковая статистика 2.44.… … Словарь-справочник терминов нормативно-технической документации

квартиль — 1.16. квартиль Квантиль порядка p = 0,25 или p = 0,75 Источник: ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения … Словарь-справочник терминов нормативно-технической документации

медиана — 3.7. медиана: Центральное значение в группе измерений, когда они расположены в порядке возрастания и их число нечетное. Если число измерений четное это среднее арифметическое двух центральных значений. Примечание Значения медиан в подгруппах… … Словарь-справочник терминов нормативно-технической документации

Статистика (функция выборки) — У этого термина существуют и другие значения, см. Статистика (значения). Статистика (в узком смысле) это измеримая числовая функция от выборки, не зависящая от неизвестных параметров распределения. В широком смысле термин (математическая)… … Википедия

Векторная авторегрессия — (VAR, Vector AutoRegression) модель динамики нескольких временных рядов, в которой текущие значения этих рядов зависят от прошлых значений этих же временных рядов. Модель предложена Кристофером Симсом как альтернатива системам одновременных… … Википедия

Источник

Q-Q Plots. От чайника до профессионала за один гайд

Как понять, что выборка данных принадлежит определенному распределению? Есть 2 метода: аналитический тест Колмогорова-Смирнова (тест Шапиро-Уилка для нормального) и графический метод при помощи графика квантиль-квантиль плот.

Чем так замечателен второй вариант? Q-Q plot позволяет кроме принадлежности:

оценить степень отклонения данных от теоретического распределения

графически проиллюстрировать такие параметры как расположение данных, масштаб и скошенность. Читаем: медиану, дисперсию и наклон функции плотности распределения.

сравнить две выборки между собой

делать выводы, не основываясь на таких спорных показателях как p.value.

Фактически, p.value в случае Q-Q Plot будет оценивать человеческий мозг на основе визуального изучения.

Графический метод является мощнейшим инструментом анализа, но как сказано в англоязычной статье википедии про Q-Q Plots, требует серьезных навыков для интерпретации. В данной статье я представляю дорожную карту пути к пониманию квантильных графиков.

С чего начинать? Сперва стоит посмотреть видео на YouTube от StatQuest. Это тот самый автор, который на обложке видеороликов пишет «. Clearly Explained». Если у вас Яндекс-браузер, то вы можете смотреть его видео почти на русском. Есть упомянутая статья в википедии, а также отличный текст на Медиуме. Мне показалось, что это лучшее, что можно найти в поиске по теории, если просто вбивать в строку браузера «Understanding QQ-Plots». Напишите в комментариях вашу любимую статью по квантильным графикам.

Несмотря на замечательные материалы, которые я упомянул, у меня не сложилось полноценного понимания QQ-Plots. Я до сих пор не могу с ходу представить в голове распределение, если мне показать квантильный график. Но в процессе их изучения я смог осознать несколько важных тезисов, с которыми и хочу вас познакомить при помощи визуализаций на Wolfram Mathematica.

В статье я представляю идеальные квантильные графики. Выводы, сделанные на их основе легко переносятся на соответствующие распределения выборочных данных в случае большого их объема (см. Рис. 1). На графиках в статье по горизонтальной оси я буду откладывать только теоретические квантили стандартного нормального распределения.

1. Квантили

Начнем с трех важнейших определений: дискретный квантиль выборки, дискретный квантиль функции плотности распределения и квантиль-функция.

Квантиль дискретной выборки — это одна из точек, делящих упорядоченную последовательность чисел на равные части.

Рис. 1: (а) и (б) Иллюстрация возможных квантилей выборки. (в) Иллюстрация квантилей, используемых для построения Q-Q Plot — самих значений выборки.

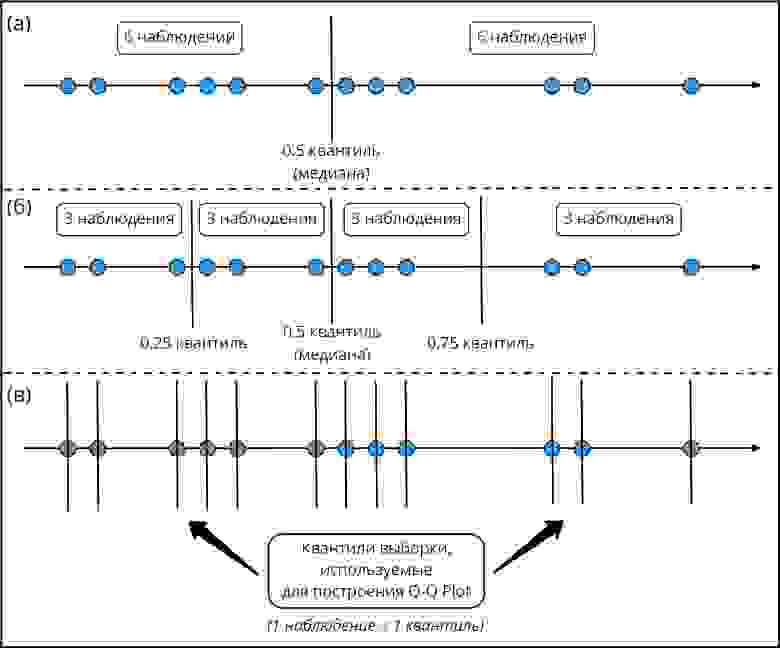
Обращаю ваше внимание, что понятия 0.25 квантиль, 1 квартиль и 25 персентиль обозначают одно и то же, как и 2 квартиль, 0.5 квантиль и 50 персентиль.

Квантиль непрерывного распределения — это одна из точек, делящих функцию плотности распределения на участки, вероятность попадания в которые одинакова, то есть на участки одинаковой площади.

Рис. 2: Иллюстрация квантилей непрерывного распределения.

Квантиль-функция — это функция, которая по значению вероятности возвращает такое число (квантиль) , что вероятность того, что случайная величина примет значение меньше равняется.

Рис. 3: Иллюстрация квантиль-функции.

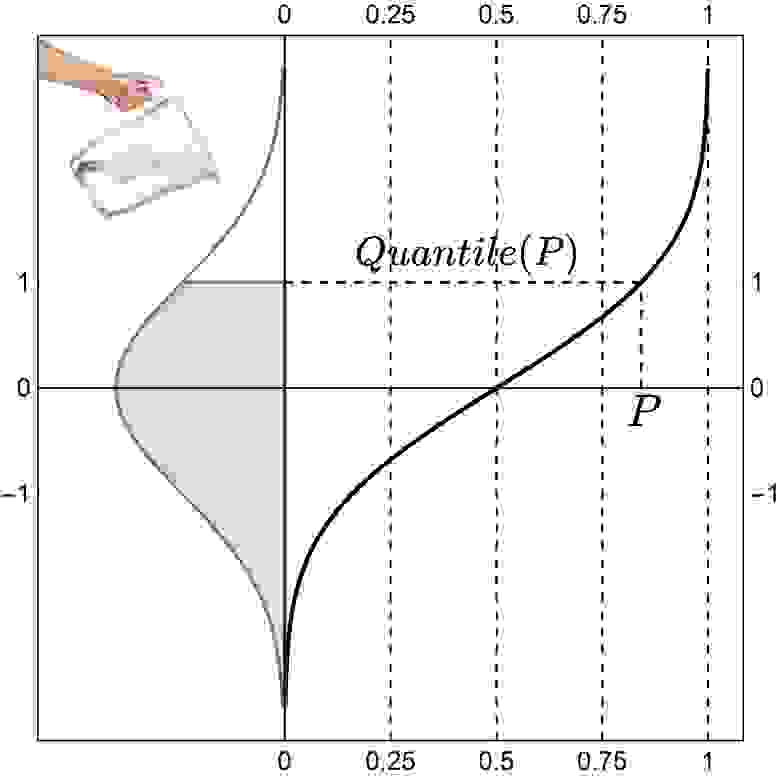
Можно представлять себе квантиль-функцию непрерывного распределения, как зависимость арифметического уровня воды в вазе, стенками которой является функция плотности вероятности от объема налитой воды. Эта интерпретация хорошо показана в видео одного бразильского инструктора по статистике.

2. Главный квантильный график

Для начала построим базовый Q-Q Plot — теоретических квантилей стандартного нормального распределения от теоретических квантилей стандартного нормального распределения. На следующей картинке (рисунок слева) в виде непрерывной прямой показана зависимость этих теоретических квантилей. Горизонтальные прямые делят распределение оси y на 8 равных по площади промежутков, а вертикальные прямые делят распределение на оси x на 8 равных промежутков и визуализируют появление непрерывной прямой, которую вы наблюдаете.

На рисунке справа я тоже построил квантильный график, но в этом случае по оси y отложил квантили выборки из 200 чисел, случайно выбранных из стандартного нормального распределения. Обращаю ваше внимание, что в случае квантильного графика выборки, за квантиль выбирается каждая точка наших данных, как показано в нижней части на рисунке 1. Далее в статье я буду опускать построение выборочного квантильного графика. Повторюсь, что на больших объемах выборки квантильный график будет полностью повторять теоретическую зависимость.

Как мы видим, в случае одинаковых распределений Q-Q Plot представляет собой прямую линию , причем масштаб нормальных распределений не имеет значения, главное, чтобы у них совпадали средние значения и стандартное отклонение. Этот вывод переносится на случай произвольных распределений.

3. Физический смысл коэффициентов прямой

Что произойдет с прямой, если у распределения на оси y поменять среднее значение (и медиану, соответственно)? Построенная прямая сместится таким образом, чтобы медиане квантилей на оси x соответствовала медиана квантилей на оси y. На рисунке слева визуально ничего не изменилось, только по оси y отложены квантили нормального распределения со средним 5 стандартным отклонением 1.

При построении Q-Q Plot от теоретических квантилей стандартного нормального распределения значение квантильной зависимости в нуле имеет смысл медианы распределения, которое мы строим на оси y.

А что произойдет с прямой, если у распределения на оси y поменять стандартное отклонение?

Рис. 6: Зависимость теоретических квантилей (а) нормального распределения N(0, 0.5) и (б) нормального распределения N(0, 2) — от теоретических квантилей стандартного нормального распределения N(0, 1).

Ответ представлен на Рисунке 6. Поигравшись с параметрами можно сделать следующий вывод:

При построении Q-Q Plot от теоретических квантилей стандартного нормального распределения тангенс наклона прямой имеет смысл стандартного отклонения распределения, которое мы строим на оси y. Если прямая положе, чем y = x (Рис. 4а), то нормальное распределение, построенное на вертикальной оси менее дисперсно, чем распределение, построенное на горизонтальной оси. Если прямая круче, чем y = x (Рис. 4б), то распределение, построенное не вертикальной оси более дисперсно, чем распределение, построенное на горизонтальной оси.

Мы разобрались с основными понятиями и выяснили, что QQ-Plot нормального распределения или выборки из нормального распределения хорошо визуализирует медиану и стандартное отклонение, чем являются коэффициенты прямой.

4. Линия главного тренда на примере скошенных распределений

Все бы хорошо, да кроме нормальных распределений есть еще много других. Если в случае построения околонормального распределения все точки стелятся вдоль прямой линии как на Рис. 4б (коэффициенты которой очень легко интерпретируются), то в случае, например, скошенных распределений точки на прямую ложиться не будут.

При построении Q-Q Plot многие программные пакеты подбирают и изображают некоторую прямую, которая называется линией главного тренда (англ. Reference Line).

Intercept и slope этой контрольной прямой имеют смысл среднего и стандартного отклонения нормального распределения, «наилучшим образом» подходящего к нашим данным. Как написано в замечательном гайде по q-q plots на языке SAS есть 3 способа это сделать:

Провести прямую по двум точкам: через 1 и 3 квартили.

Провести прямую методом наименьших квадратов.

К выборочным данным подобрать среднее и стандартное отклонение генеральной совокупности, используя метод максимального правдоподобия и провести прямую, иллюстрирующую зависимость теоретических квантилей подобранного идеального нормального распределения от теоретических квантилей стандартного нормального (или любого другого, используемого при построении).

Мнение автора по интерпретации 1 и 2 способа.

В первом случае «идеальная прямая» будет соответствовать нормальному распределению со средним, равным среднему значению 1 и 3 квартилей выборки и стандартным отклонением, равным отношению межквартильного размаха распределения на оси y и межквартильного размаха распределения на оси x.

где IQR(x) и IQR(y) — межквартильный размах распределений, построенных на осях y и x соответственно. Для стандартного нормального распределения IQR(x) примерно равен 1.35.

Во втором случае тангенс наклона прямой будет равен произведению корреляции квантилей изображенных распределений — на стандартное отклонение распределения на оси y.

где corr — корреляция, а sd — стандартное отклонение. Это следует из формул для коэффициентов регрессионной прямой, а также из того факта, что для стандартного нормального распределения sd(x) = 1.

Я не нашел подтверждения полученных умозаключений в литературе и не представляю, как использовать эту информацию в реальном анализе.

Разные программные пакеты строят эту линию, используя один из указанных подходов. Если есть большая потребность узнать методы построения, можно заглянуть в документацию. Но если это не принципиально, можно ориентироваться на главную идею: линия главного тренда представляет прямую идеального нормального распределения для наших данных.

Выводы:

Если оба конца квантильного графика находятся выше прямой главного тренда, то скорее всего это распределение скошено вправо.

Если оба конца квантильного графика находится ниже прямой главного тренда, то скорее всего это распределение скошено влево.

5. Изогнутые Q-Q Plots: Равномерное, Бимодальное и t-распределения.

Следующие 4 графика предназначены для настройки машинного обучения в голове. С помощью них можно научиться отличать равномерное распределение от двугорбого.

Рис. 8: Зависимость теоретических квантилей (a) равномерного распределения Uniform(-1, 1) (б) равномерного распределение Uniform(-2,2) (в) бимодального распределения из двух нормальных N(-1,0.5) и N(1, 0.5) и (г) бимодального распределения из двух нормальных N(-1, 0.3) и N(1, 0.3) — от теоретических квантилей стандартного нормального распределения N(0, 1)

Квантиль-квантиль плот для равномерного и бимодальных распределений представляют собой — Образную кривую. В случае равномерного распределения кривая стелется вдоль линии главного тренда, а в случае бимодального пересекает ее. Обращаю также ваше внимание на поведение буквы в нуле в случае бимодального распределения. Если разрыв между горбами велик, то квантильная зависимость в этом месте становится почти вертикальной.

Стоит прямо здесь научиться распознавать распределение Стьюдента, которое, как известно имеет более толстые хвосты, по сравнению со стандартным нормальном. Внимание на экран.

Рис. 9: Зависимость теоретических квантилей (а) распределения Стьюдента с 2 степенями свободы и (б) распределения Стьюдента с 6 степенями свободы — от теоретических квантилей стандартного нормального распределения N(0, 1).

Здесь мы тоже видим змееобразную кривую, но она представляет собой букву зеркально-отраженную относительно линии главного тренда.

Бонус: Экспоненциальное распределение

На следующем рисунке изображён первый график из англоязычной статьи Википедии про Q-Q Plots. Обращаю еще раз ваше внимание на то, что значение квантильного графика в нуле — это медиана распределения, которое мы строим вдоль оси y. На данном квантильном графике не изображена линия главного тренда. Пунктирная прямая представляет график функции y = x.

Заключение

Если делать summary, то главным является следующее.

Если точки на графике Q-Q Plot стелятся вдоль какой-то прямой, то наши данные неплохо соответствуют теоретическим квантилям, отложенным по горизонтальной оси.

Если мы строим Q-Q Plot от теоретических квантилей стандартного нормального распределения, то:

Значение получившейся функции в нуле — это медиана нашей выборки. Вообще все квантили нашей выборки соответствуют квантилям распределения на оси x, а не только медиана 🙂

Тангенс линии тренда соответствует стандартному отклонению нормального распределения, наилучшим образом описывающем нашу выборку. Значение линии главного тренда в нуле соответствует его среднему значению

Я буду рад, если моя статья поможет кому-то в понимании QQ-Plots. Поделитесь в комментариях вашим любимым учебным материалом по квантильным графикам или примером реального их использования в анализе данных.

Благодарю Анастасию Котликову за ценное обсуждение способов построения линии главного тренда и за помощь в интерпретации ее коэффициентов.

Источник

Квантили распределений EXCEL

history 19 ноября 2016 г.

Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в MS EXCEL .

Сначала дадим формальное определение квантиля, затем приведем примеры их вычисления в MS EXCEL.

Определение

Точное значение квантиля в нашем случае можно найти с помощью формулы =НОРМ.СТ.ОБР(0,21)

СОВЕТ : Процедура вычисления квантилей имеет много общего с вычислением процентилей выборки (см. статью Процентили в MS EXCEL ).

Квантили специальных видов

Часто используются Квантили специальных видов:

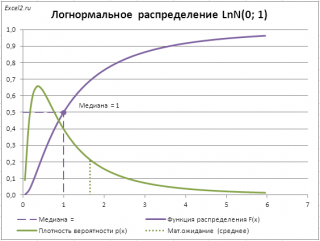
В качестве примера вычислим медиану (0,5-квантиль) логнормального распределения LnN(0;1) (см. файл примера лист Медиана ).

Это можно сделать с помощью формулы =ЛОГНОРМ.ОБР(0,5; 0; 1)

Квантили стандартного нормального распределения

Необходимость в вычислении квантилей стандартного нормального распределения возникает при проверке статистических гипотез и при построении доверительных интервалов.

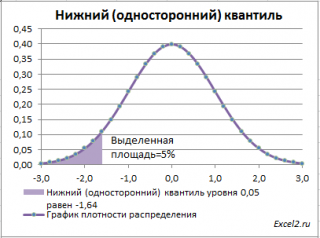
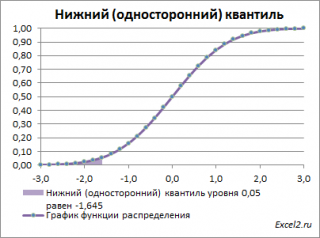
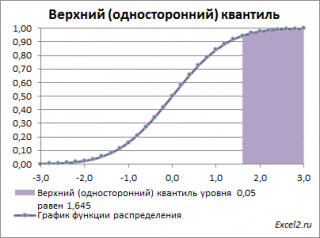
В данных задачах часто используется специальная терминология:

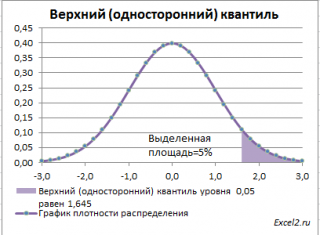
Однако, при проверке гипотез и построении доверительных интервалов чаще используется «верхний» α-квантиль. Покажем почему.

Действительно, для α=0,05, верхний 0,05-квантиль стандартного нормального распределения равен 1,645. Т.к. функция плотности вероятности стандартного нормального распределения является четной функцией, то вычисления в MS EXCEL верхнего квантиля можно сделать по двум формулам:

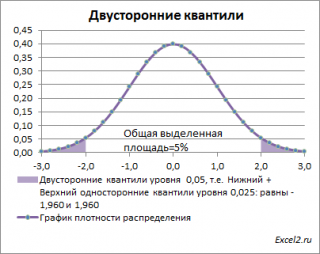
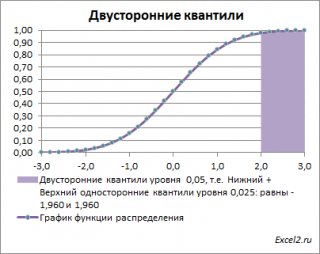
Другими словами, двусторонние α-квантили задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.

Квантили распределения Стьюдента

Квантили распределения ХИ-квадрат

Вычислять квантили распределения ХИ-квадрат с n -1 степенью свободы требуется, если проводится проверка гипотезы о дисперсии нормального распределения (см. статью Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения ).

Результат равен 3,25.

Квантили F-распределения

Вычислять квантили распределения Фишера с n ₁ -1 и n ₂ -1 степенями свободы требуется, если проводится проверка гипотезы о равенстве дисперсий двух нормальных распределений (см. статью Двухвыборочный тест для дисперсии: F-тест в MS EXCEL ).

Чтобы вычислить верхний 0,05/2-квантиль для F -распределения с числом степеней свободы 10 и 12, необходимо записать формулу =F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)

Квантили распределения Вейбулла

После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:

Квантили экспоненциального распределения

Задача : Случайная величина имеет экспоненциальное распределение :

Требуется выразить p -квантиль x _p через параметр распределения λ и заданную вероятность p .

Решение : Вспоминаем, что p -квантиль – это такое значение x _p случайной величины X, для которого P(X

Источник