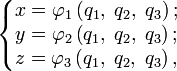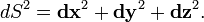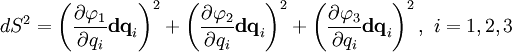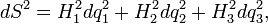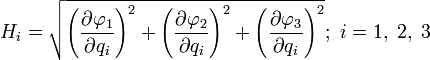Что такое криволинейные координаты

Магия тензорной алгебры: Часть 3 — Криволинейные координаты

Введение

Читая отзывы к своим статьям, понял, что я излишне перегрузил читателя теоретическими вводными. Прошу за это прощения, признаться честно, я сам далек от формальной математики.

Однако, тензорное исчисление пестрит понятиями, многие из которых требуется вводить формально. Поэтому третья статься цикла тоже будет посвящена сухой теории. Тем не менее, я обещаю, что в следующей работе приступлю к тому, к чему сам давно хотел — к описанию практической ценности тензорного подхода. На примете имеется интересная задача, большая часть которой в моей голове уже разобрана. Тензорное исчисление для меня не праздный интерес, а способ обработать некоторые из своих теоретических и практических соображений в области механики. Так что практика по полной программе ещё предстоит.

А пока что рассмотрим некоторые теоретические основы. Добро пожаловать под кат.

1. Матрица Якоби и локальная метрика. «Жонглирование» индексами

Те системы координат, что мы рассматривали до сих пор были косоугольными. Но их оси были прямыми линиями. Однако, крайне часто приходится работать в пространстве, координатные линии которого — кривые. Такая система координат называется криволинейной.

Простейший жизненный пример криволинейной системы координат — географические координаты — широта, долгота и высота над уровнем моря, по которой определяется положение объектов вблизи поверхности Земли. Криволинейные координаты широко применяются в астрономии. В механике примером таких координат могут служить обобщенные координаты механической системы, однозначно определяющие её положение в пространстве с учетом геометрии наложенных на систему связей. На этом и строится аналитическая механика.

Рис. 1. Криволинейные координаты в трехмерном пространстве

Рассмотрим криволинейные координаты, заданные в трехмерном евклидовом пространстве (рисунок 1). Пусть положение точки задается в этих координатах вектором

и декартовы координаты точки связаны с (1) соотношением

или, в компонентной форме

Рассмотрим частную производную . Результат такого дифференцирования — это вектор, направленный по касательной к координатной линии . Дифференцируя (2) по всем криволинейным координатам получим тройку векторов

Эти векторы задают базис так называемого касательного пространства. И в отличие от базиса в косоугольной системе координат, модуль и направление этих векторов будут изменятся при переходе от одной точки к другой. Мы получаем переменный базис, зависящий от положения в пространстве, заданного вектором (1). Такой базис называется локальным

Векторы (4) собирают в матрицу

которая называется матрицей Якоби, и по сути определяется как производная от одного вектора по другому вектору. В нашем случае

Легко догадаться, что если функция (2) линейна относительно компонент вектора , то её можно выразить матричным соотношением

то мы рассматриваем косоугольную систему координат, и матрица Якоби будет равна матрице преобразования от косоугольных координат к декартовым

Теперь, любой вектор, заданный в пространстве (тензор ранга (1, 0)) можно представить через его контравариантные компоненты в криволинейной системе координат

Однако, компоненты вектора, из-за переменного базиса, будут зависеть от положения в пространстве точки приложения вектора. Кроме того, для того чтобы представление (6) существовало, надо чтобы векторы, составляющие базис были не компланарны. Из курса векторной алгебры нам известно, что векторы некомпланарны, если их смешанное произведение отлично от нуля. Отсюда возникает условие, которому должен удовлетворять определитель матрицы Якоби

Данный определитель как раз определяет смешанное произведение векторов базиса.

Теперь вычислим ковариантные компоненты вектора . Для этого, в самой первой статье цикла, мы умножали вектор скалярно на соответствующий вектор базиса

В той же, первой статье, мы определили, что ковариантные компоненты вектора связаны с контравариантными через метрический тензор

Сравнивая два последних выражения мы получаем определение метрического тензора в криволинейных координатах

которое можно представить в матричной форме

Эту связь можно представить и в тензорной форме, но для этого придется ввести явно метрику для декартовых координат

Тогда, преобразование декартовой метрики в криволинейную будет выглядеть так

Выражение (8) вводит метрический тензор для криволинейных координат. Этот тензор зависит от положения точки в пространстве, поэтому говорят что он задан локально или определяет локальную метрику

Определившись с метрикой, мы можем записать правила преобразования контравариантных координат в ковариантные

и ковариантных координат в контравариантные

В тензорном исчислении операции опускания (9) и поднятия (10) индексов называют «жонглированием» индексами.

Выписав соотношения (9) и (10) мы подразумевали, что матрицы и взаимно обратимы. Это возможно лишь в том случае, если

Данное условие выполняется для криволинейных координат, если матрица Якоби не вырождена, и это непосредственно следует из (8), так как

то есть условие (7) выполняемое для всех точек пространства — достаточное условие невырожденности локальной метрики.

Рассмотрение вырожденнных метрик, это отдельный и сложный вопрос, поэтому мы ограничимся метриками, в которых матрица метрического тензора обратима, то есть выполняется условие

2. Взаимный базис

Введем векторы , получаемые из векторов исходного базиса путем поднятия индекса

Теперь возьмем и умножим (11) скалярно на вектор

но, мы знаем, что — метрический тензор, поэтому, приходим к уравнению

Если мы возьмем, например, вектор , то в силу (12) он перпендикулярен векторам и (его скалярное произведение с ними равно нулю), а скалярное произведение этого вектора на — равно единице

Дальше возьмем и умножим (11) скалярно на

и в силу (12) это дает контравариантный метрический тензор

Система векторов тоже образует базис, который называют взаимным или сопряженным с базисом .

Снова рассмотрим вектор . Из соотношений (10) и (11) следует цепочка преобразований

Умножим (13) скалярно на

приходим к заключению, что любой вектор может быть разложен как по базису — тогда его компоненты будут контравариантные, так и по базису — компоненты будут ковариантными

При этом, ковариантные компоненты — это скалярные произведение вектора на векторы базиса , а контравариантные компоненты — скалярные произведения вектора на векторы базиса

что ещё раз иллюстрирует взаимность этих базисов.

Тут надо отметить, что векторы базиса получаются естественным путем — они касательны соответствующим координатным линиям и им можно приписать геометрический смысл. Что касается базиса , то его векторы не направлены по касательной координатным линиям, а перпендикулярны парам векторов касательного базиса. Такой базис иногда принято называть неголономным

3. Преобразование криволинейных координат. Формальное определение ковариантных и контравариантных компонент

Допустим, что мы работаем в криволинейной система координат, определенной вектором . Перейдем к другой системе координат, положение точек которой определяется вектором , таким, что преобразование от старой системы координат к новой определяется уравнениями

Будем считать преобразование (16) обратимым, то есть допустим существование функции

Для этого требуется, чтобы определитель матрицы Якоби

был отличен от нуля

Тогда существует матрица , обратная матрице (18), такая, что

Матрица является матрицей Якоби для преобразования (17). Тогда можно вычислить векторы нового базиса

Получаем связь между старым базисом и новым

Разложим вектор в новом базисе

и используя соотношение (19), напишем

С учетом того, что векторы базиса линейно независимы, приравниваем коэффициенты при них в (21)

Теперь умножим обе части (21) на

То есть, получаем формулу обратного преобразования контравариантных компонент

Контравариантные компоненты вектора преобразуются оператором, обратным оператору преобразования базиса

Действительно, чтобы получить векторы нового базиса, мы использовали матрицу по формуле (19). Чтобы получить контравариантные компоненты заданного в новом базисе вектора мы используем матрицу

А теперь посмотрим, как преобразуется вектор, заданный своими ковариантными компонентами

Ковариантные компоненты вектора преобразуются тем же оператором, которым осуществляется преобразование базиса

Тензор ранга (1,0) преобразуется оператором обратным, используемому при преобразовании базиса, а тензор ранга (0,1) преобразуется тем же самым оператором, что используется при преобразовании базиса.

4. Ковариантная производная. Символы Кристоффеля 2-го рода

Предположим, что мы хотим продифференцировать вектор, заданный произвольными координатам по какой-то из координат. Что мы должны сделать? Давайте попробуем выполнить эту операцию

На каком основании мы выписали производную от базисного вектора? А на том основании, что базис в криволинейных координатах зависит от них, а значит его производная от координаты отлична от нуля. Ну и ладно, эта производная тоже будет вектором, а значит её можно разложить по локальному базису, например вот так

Найдем коэффициенты разложения в (25). Для этого, возьмем ковариантный метрический тензор и продифференцируем его по указанной координате

Здесь очевидно присутствие компонент метрического тензора, поэтому выполняем замену

Прежде чем начать работать с (27), скажем, что искомые коэффициенты разложения симметричны относительно нижних индексов, так как проведя прямое дифференцирования базисного вектора приходим к выражению

откуда, в силу непрерывности рассматриваемых функций, заключаем, что

Теперь, в (27) переставим индексы i и k

А теперь, переставим в (27) индексы j и k

Теперь сложим (29) и (30) учтя при этом симметричность (28)

Вычитаем (27) из (31), снова учитывая (28)

Умножаем (32) на , и получаем окончательно

Выражение (33) определяет так называемый символ Кристоффеля 2-го рода. Тогда

Выражение, стоящее в скобках в (34) называется ковариантной производной контравариантных компонент вектора

Исходя из (35) мы должны понимать, что пытаясь дифференцировать по криволинейной координате, мы обязаны учитывать зависимость базиса от координат. Если метрика не зависит от положения точки приложения вектора в пространстве, то (35) превращается в частную частную производную, ибо все символы Кристоффеля равны будут нулю, из-за того что метрический тензор не зависит от координат. В любой косоугольной системе координат, и в их частном случае — декартовых координатах, символы Кристоффеля, согласно (33) равны нулю. А значит, согласно (35) ковариантрая производная от вектора по координате будет совпадать с его частной производной по этой координате, к чему мы приучены вобщем-то давно. Но если бы (33) был тензором, то он, будучи равен нулю, остался бы нулевым в любой другой системе координат. Но в криволинейных координатах (33) нулю не равны. А значит символы Кристоффеля не являются тензором. При преобразовании системы координат меняются компоненты, но не сущность тензора. Нулевой тензор должен быть таковым в любой системе координат.

Заключение

Первичные теоретические основы разобраны. Со следующей статьи мы уйдем в практику использования тензорного исчисления для решения конкретных задач. Спасибо Вам за оказанное мне внимание и доверие.

Источник

криволинейные координаты

Смотреть что такое «криволинейные координаты» в других словарях:

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ — координаты точки на плоскости, на поверхности или в пространстве, отличные от прямолинейных (декартовых) координат. На плоскости (поверхности) криволинейные координаты определяются при помощи таких двух семейств кривых (координатных линий), что… … Большой Энциклопедический словарь

Криволинейные координаты — Пусть x, y, z декартовы координаты. Пусть q1, q2, q3 произвольные ортогональные криволинейные координаты. Пусть также справедливы соотношения: где … Википедия

криволинейные координаты — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN curvilinear coordinates … Справочник технического переводчика

криволинейные координаты — kreivinės koordinatės statusas T sritis fizika atitikmenys: angl. curvilinear coordinates vok. krummlinige Koordinaten, f rus. криволинейные координаты, f pranc. coordonnées curvilignes, f … Fizikos terminų žodynas

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ — координаты точки на плоскости, на поверхности или в пространстве, отличные от прямолинейных (декартовых) координат. На плоскости (поверхности) К. к. определяются при помощи таких двух семейств кривых (координатных линий), что любая кривая одного… … Естествознание. Энциклопедический словарь

Криволинейные координаты — см. Координаты … Большая советская энциклопедия

прямоугольные криволинейные координаты — stačiakampės kreivinės koordinatės statusas T sritis fizika atitikmenys: angl. curvilinear orthogonal coordinates; orthogonal curvilinear coordinates vok. rechtwinklige krummlinige Koordinaten, f rus. прямоугольные криволинейные координаты, f… … Fizikos terminų žodynas

Координаты (математ.) — Координаты [от лат. co (cum) ≈ совместно и ordinatus ≈ упорядоченный, определённый], числа, заданием которых определяется положение точки на плоскости, на любой поверхности или в пространстве. Первыми вошедшими в систематическое употребление К.… … Большая советская энциклопедия

КООРДИНАТЫ — (от лат. co совместно и ordinatus упорядоченный определенный), числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. Прямоугольные (декартовы) координаты точки на плоскости суть снабженные знаками + … Большой Энциклопедический словарь

Источник

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ

Смотреть что такое «КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ» в других словарях:

Криволинейные координаты — Пусть x, y, z декартовы координаты. Пусть q1, q2, q3 произвольные ортогональные криволинейные координаты. Пусть также справедливы соотношения: где … Википедия

криволинейные координаты — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN curvilinear coordinates … Справочник технического переводчика

криволинейные координаты — координаты точки на плоскости, на поверхности или в пространстве, отличные от прямолинейных (декартовых) координат. На плоскости (поверхности) криволинейные координаты определяются при помощи таких двух семейств кривых (координатных линий), что… … Энциклопедический словарь

криволинейные координаты — kreivinės koordinatės statusas T sritis fizika atitikmenys: angl. curvilinear coordinates vok. krummlinige Koordinaten, f rus. криволинейные координаты, f pranc. coordonnées curvilignes, f … Fizikos terminų žodynas

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ — координаты точки на плоскости, на поверхности или в пространстве, отличные от прямолинейных (декартовых) координат. На плоскости (поверхности) К. к. определяются при помощи таких двух семейств кривых (координатных линий), что любая кривая одного… … Естествознание. Энциклопедический словарь

Криволинейные координаты — см. Координаты … Большая советская энциклопедия

прямоугольные криволинейные координаты — stačiakampės kreivinės koordinatės statusas T sritis fizika atitikmenys: angl. curvilinear orthogonal coordinates; orthogonal curvilinear coordinates vok. rechtwinklige krummlinige Koordinaten, f rus. прямоугольные криволинейные координаты, f… … Fizikos terminų žodynas

Координаты (математ.) — Координаты [от лат. co (cum) ≈ совместно и ordinatus ≈ упорядоченный, определённый], числа, заданием которых определяется положение точки на плоскости, на любой поверхности или в пространстве. Первыми вошедшими в систематическое употребление К.… … Большая советская энциклопедия

КООРДИНАТЫ — (от лат. co совместно и ordinatus упорядоченный определенный), числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. Прямоугольные (декартовы) координаты точки на плоскости суть снабженные знаками + … Большой Энциклопедический словарь

Источник

Криволинейные координаты

Криволинейные координаты

где 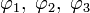— некоторые функции.

Дифференциал дуги в декартовых координатах имеет вид:

Тогда можно записать дифференциал дуги в криволинейных координатах в виде (используется правило суммирования Эйнштейна):

Принимая во внимание ортогональность систем координат ( 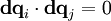при ) это выражение можно переписать в виде

Полезное

Смотреть что такое «Криволинейные координаты» в других словарях:

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ — координаты точки на плоскости, на поверхности или в пространстве, отличные от прямолинейных (декартовых) координат. На плоскости (поверхности) криволинейные координаты определяются при помощи таких двух семейств кривых (координатных линий), что… … Большой Энциклопедический словарь

криволинейные координаты — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN curvilinear coordinates … Справочник технического переводчика

криволинейные координаты — координаты точки на плоскости, на поверхности или в пространстве, отличные от прямолинейных (декартовых) координат. На плоскости (поверхности) криволинейные координаты определяются при помощи таких двух семейств кривых (координатных линий), что… … Энциклопедический словарь

криволинейные координаты — kreivinės koordinatės statusas T sritis fizika atitikmenys: angl. curvilinear coordinates vok. krummlinige Koordinaten, f rus. криволинейные координаты, f pranc. coordonnées curvilignes, f … Fizikos terminų žodynas

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ — координаты точки на плоскости, на поверхности или в пространстве, отличные от прямолинейных (декартовых) координат. На плоскости (поверхности) К. к. определяются при помощи таких двух семейств кривых (координатных линий), что любая кривая одного… … Естествознание. Энциклопедический словарь

Криволинейные координаты — см. Координаты … Большая советская энциклопедия

прямоугольные криволинейные координаты — stačiakampės kreivinės koordinatės statusas T sritis fizika atitikmenys: angl. curvilinear orthogonal coordinates; orthogonal curvilinear coordinates vok. rechtwinklige krummlinige Koordinaten, f rus. прямоугольные криволинейные координаты, f… … Fizikos terminų žodynas

Координаты (математ.) — Координаты [от лат. co (cum) ≈ совместно и ordinatus ≈ упорядоченный, определённый], числа, заданием которых определяется положение точки на плоскости, на любой поверхности или в пространстве. Первыми вошедшими в систематическое употребление К.… … Большая советская энциклопедия

КООРДИНАТЫ — (от лат. co совместно и ordinatus упорядоченный определенный), числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. Прямоугольные (декартовы) координаты точки на плоскости суть снабженные знаками + … Большой Энциклопедический словарь

Источник